С понятием прямой линии тесно связано понятие ее направляющего вектора. Часто в задачах бывает удобнее рассматривать его вместо самой прямой. В рамках данного материала мы разберем, что же такое направляющий вектор прямой в пространстве и на плоскости, и расскажем, для чего можно его использовать.
В первом пункте мы сформулируем определение и покажем основные понятия на иллюстрациях, дополнив их конкретными примерами направляющего вектора. Далее мы посмотрим, как прямая и направляющие векторы взаимодействуют в прямоугольной системе координат и как можно вычислить координаты этого вектора, если мы знаем уравнение прямой. Все правила, как всегда, будут проиллюстрированы примерами решений задач.
- Что такое направляющий вектор прямой
- Как вычислить координаты направляющего вектора по уравнениям прямой
- Уравнение прямой
- Уравнение прямой на плоскости
- Уравнение прямой с угловым коэффициентом
- Уравнение прямой в отрезках на осях
- Уравнение прямой, проходящей через две различные точки на плоскости
- Параметрическое уравнение прямой на плоскости
- Каноническое уравнение прямой на плоскости
- Уравнение прямой в пространстве
- Уравнение прямой, проходящей через две различные точки в пространстве
- Параметрическое уравнение прямой в пространстве
- Каноническое уравнение прямой в пространстве
- Прямая как линия пересечения двух плоскостей
- Прямая в пространстве – виды уравнения прямой в пространстве
- Параметрическое и каноническое уравнение прямой в пространстве
- Уравнение прямой в пространстве, которая проходит через две заданные точки
- Общее уравнение прямой – переход к каноническому уравнению
- Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых
- Примеры решения задач
- 🎥 Видео
Видео:Видеоурок "Канонические уравнения прямой"Скачать

Что такое направляющий вектор прямой
Для того чтобы понять эту тему, нам нужно хорошо представлять, что такое вообще прямая и как она может размещаться в пространстве и на плоскости. Кроме того, важно вспомнить ранее изученное понятие вектора. Об этом мы уже писали в отдельном материале. Если нужно, найдите и перечитайте эти статьи.
Сформулируем, что такое направляющий вектор.
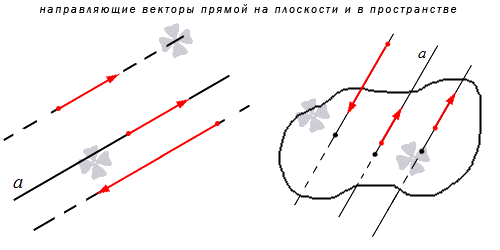
Направляющим вектором прямой является любой вектор, не равный нулю, который размещается на данной прямой или же на прямой, параллельной ей.
Получается, что у каждой прямой есть бесконечное множество направляющих векторов. При этом все они будут являться коллинеарными в силу озвученного определения, ведь они лежат на одной прямой или параллельной ей другой прямой. Выходит, что если a → является направляющий вектором прямой a , то другой направляющий вектор мы можем обозначить как t · a → при любом значении t , соответствующем действительному числу.
Также из определения выше можно сделать вывод, что направляющие векторы двух параллельных прямых будут совпадать: если прямые a и a 1 являются параллельными, то вектор a → будет направляющим и для a , и для a 1 .
Третий вывод, следующий из определения: если у нас есть направляющий вектор прямой a , то он будет перпендикулярным по отношению к любому нормальному вектору той же прямой.
Приведем пример направляющего вектора: в прямоугольной системе координат для осей O x , O y и O z направляющими будут координатные векторы i → , j → и k → .
Видео:Геометрия. 9 класс. Уравнение прямой. Направляющий вектор и вектор нормали прямой /22.10.2020/Скачать

Как вычислить координаты направляющего вектора по уравнениям прямой
Допустим, что у нас есть некая прямая с направляющими векторами, лежащая в прямоугольной системе координат. Сначала мы разберем случай с плоской декартовой системой O x y , а потом с системой O x y z , расположенной в трехмерном пространстве.
1. Прямую линию в O x y можно описать с помощью уравнения прямой на плоскости. В этом случае координаты направляющих векторов будут соответствовать направляющим векторам исходной прямой. А если нам известно уравнение прямой, как вычислить координаты ее направляющего вектора? Это легко сделать, если мы имеем дело с каноническим или параметрическим уравнением.
Допустим, у нас есть канонический случай уравнения, которое имеет вид x — x 1 a x = y — y 1 a y . С его помощью на плоскости задана прямая с направляющим вектором a → = ( a x , a y ) .
Чтобы вычислить координаты направляющего вектора, нам нужно взять числа из знаменателя канонического уравнения прямой.
Приведем пример задачи.
В прямоугольной системе координат задана прямая, которую можно описать уравнением x — 1 4 = y + 1 2 — 3 . Вычислите координаты одного из направляющих векторов прямой.
Решение
Из уравнения мы можем сразу взять координаты направляющего вектора. Берем числа в знаменателях и записываем: 4 , — 3 . Это и будет нужный нам ответ.
Ответ: 4 , — 3 .
Если же прямая описана уравнением параметрического типа, то нам нужно смотреть на коэффициенты при параметре. Они будут соответствовать координатам нужного нам направляющего вектора.
У нас есть прямая, которую можно описать с помощью системы параметрических уравнений x = — 1 y = 7 — 5 · λ , при этом λ ∈ R . Найдите координаты направляющих векторов.
Решение
Для начала перепишем данные параметрические уравнения в виде x = — 1 + 0 · λ y = 7 — 5 · λ . Посмотрим на коэффициенты. Они сообщат нам нужные координаты направляющего вектора – a → = ( 0 , 5 ) . Учитывая, что все направляющие векторы одной прямой будут коллинеарны, мы можем задать их в виде t · a → или 0 , — 5 · t , где t может быть любым действительным числом. О том, как проводить действия с векторами в координатах, мы писали в отдельной статье.
Ответ: 0 , — 5 · t , t ∈ R , t ≠ 0
Теперь разберем случай, как найти координаты вектора, если прямая задана общим уравнением вида A x + B y + C = 0 . Если A = 0 , то исходное уравнение можно переписать как B y + C = 0 . Оно определяет прямую, которая будет параллельна оси абсцисс. Значит, в качестве ее направляющего вектора мы можем взять координатный вектор i → = 1 , 0 .
А если B = 0 , то уравнение прямой мы можем записать как A x + C = 0 . Описываемая им прямая будет параллельна оси ординат, поэтому ее координатный вектор j → = 0 , 1 также будет направляющим. Рассмотрим конкретную задачу.
У нас есть прямая, заданная при помощи общего уравнения x — 2 = 0 . Найдите координаты любого направляющего вектора.
Решение
В прямоугольной системе координат исходное уравнение будет соответствовать прямой, параллельной оси ординат. Значит, мы можем взять координатный вектор j → = ( 0 , 1 ) . Он будет для нее направляющим.
Ответ: ( 0 , 1 )
А как быть в случае, если ни один коэффициент в A x + B y + C = 0 не будет равен 0? Тогда мы можем использовать несколько разных способов.
1. Мы можем переписать основное уравнение так, чтобы оно превратилось в каноническое. Тогда координаты вектора можно будет взять из его значений.
2. Можно вычислить отдельно начальную и конечную точку направляющего вектора. Для этого надо будет взять координаты двух любых несовпадающих точек исходной прямой.
3. Третий способ заключается в вычислении координат любого вектора, который будет перпендикулярен нормальному вектору этой прямой n → = A , B .
Самым простым является первый подход. Проиллюстрируем его на примере задачи.
Есть прямая на плоскости, заданная уравнением 3 x + 2 y — 10 = 0 . Запишите координаты любого направляющего вектора.
Решение
Перепишем исходное уравнение в каноническом виде. Сначала перенесем все слагаемые из левой части, кроме 3 x, в правую с противоположным знаком. У нас получится:
3 x + 2 y — 10 = 0 ⇔ 3 x = — 2 y + 10
Получившееся равенство преобразовываем и получаем:
3 x = — 2 y + 10 ⇔ 3 x = — 2 ( y — 5 ) ⇔ x — 2 = y — 5 3
Отсюда мы уже можем вывести координаты нужного нам направляющего вектора: -2 , 3
К общему виду легко свести и такие типы уравнений, как уравнение прямой в отрезках x a + y b = 1 и уравнение прямой с угловым коэффициентом y = k · x + b , так что если они встретились вам в задаче на нахождение координат направляющего вектора, то можно также использовать этот подход.
Далее мы разберем, как найти эти координаты, если прямая у нас задана не в плоскости, а в пространстве.
Вектор a → = ( a x , a y , a z ) является направляющим для прямой, выраженной с помощью:
1) канонического уравнения прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z
2) параметрического уравнения прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z
Таким образом, для вычисления координат направляющего вектора нужно взять числа из знаменателей или коэффициентов при параметре в соответствующем уравнении.
Рассмотрим конкретную задачу.
Прямая в пространстве задана уравнением вида x — 1 4 = y + 1 2 0 = z — 3 . Укажите, какие координаты будет иметь направляющий вектор данной прямой.
Решение
В каноническом уравнении необходимые числа видны сразу в знаменателях. Получается, что ответом будет вектор с координатами 4 , 0 , — 3 . Координаты всех направляющих векторов данной прямой можно записать в виде 4 · t , 0 , — 3 · t при условии, что t является действительным числом.
Ответ: 4 · t , 0 , — 3 · t , t ∈ R , t ≠ 0
Вычислите координаты любого направляющего вектора для прямой, которая задана в пространстве с помощью параметрического уравнения x = 2 y = 1 + 2 · λ z = — 4 — λ .
Решение
Перепишем данные уравнения в виде x = 2 + 0 · λ y = 1 + 2 · λ z = — 4 — 1 · λ .
Из этой записи можно вычленить координаты нужного нам вектора – ими будут коэффициенты перед параметром.
Разберем еще один случай. Как вычислить нужные координаты, если прямая задана уравнением двух пересекающихся плоскостей вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 ?
Есть два способа. Можно записать это уравнение в параметрическом виде, где будут видны нужные координаты. Но можно использовать и другой способ. Объясним его.
Вспомним, что такой нормальный вектор плоскости. Он по определению будет лежать на прямой, перпендикулярной исходной плоскости. Значит, любой направляющий вектор прямой, которая в ней находится, будет перпендикулярен ее любому нормальному вектору.
Направляющий вектор прямой, образованной пересечением двух плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , будет перпендикулярен нормальным векторам n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) . То есть в качестве направляющего вектора мы может взять произведение векторов n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .
n 1 → × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2 — это и есть направляющий вектор прямой, по которой пересекаются исходные плоскости.
Решим задачу, в которой применяется этот подход.
Запишите координаты направляющего вектора прямой, выраженной с помощью уравнения x + 2 y + 3 z — 1 = 0 2 x + 4 y — 4 z + 5 = 0 .
Решение
Возьмем произведение двух нормальных векторов плоскостей x + 2 y + 3 z — 1 = 0 и 2 x + 4 y — 4 z + 5 = 0 . У них следующие координаты: 1 , 2 , 3 и 2 , 4 , — 4 .
У нас получится:
n 1 → × n 2 → = i → j → k → 1 2 3 2 4 — 4 = i → · 2 · ( — 4 ) + j → · 3 · 2 + k → · 1 · 4 — — k → · 2 · 2 — i → · 3 · 4 — j → · 1 · ( — 4 ) = — 20 · i → + 10 · j → + 0 · k →
Выходит, что вектор n 1 → × n 2 → = — 20 · i → + 10 · j → + 0 · k → ⇔ n 1 → × n 2 → = — 20 , 10 , 0 – это и есть нужный нам направляющий вектор прямой.
Ответ: — 20 , 10 , 0
В конце статьи отметим, что умение вычислять направляющий вектор пригодится для решения многих задач, таких, как сопоставление двух прямых, доказательство их параллельности и перпендикулярности, вычисление угла между пересекающимися или скрещивающимися прямыми и др.
Видео:11. Прямая в пространстве и ее уравненияСкачать

Уравнение прямой
Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
где A и B не могут быть одновременно равны нулю.
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.
Уравнение прямой в отрезках на осях
Если прямая пересекает оси OX и OY в точках с координатами ( a , 0) и (0, b ), то она может быть найдена используя формулу уравнения прямой в отрезках
| x | + | y | = 1 |
| a | b |
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки M( x 1, y 1) и N( x 2, y 2), такие что x 1 ≠ x 2 и y 1 ≠ y 2, то уравнение прямой можно найти, используя следующую формулу
| x — x 1 | = | y — y 1 |
| x 2 — x 1 | y 2 — y 1 |
Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
x = l t + x 0 y = m t + y 0
где N( x 0, y 0) — координаты точки лежащей на прямой, a = — координаты направляющего вектора прямой.
Каноническое уравнение прямой на плоскости
Если известны координаты точки N( x 0, y 0) лежащей на прямой и направляющего вектора a = ( l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу
| x — x 0 | = | y — y 0 |
| l | m |
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
x — 1 2 — 1 = y — 7 3 — 7
Упростив это уравнение получим каноническое уравнение прямой
Выразим y через x и получим уравнение прямой с угловым коэффициентом
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
x = t + 1 y = -4 t + 7
Решение. Так как M y — N y = 0, то невозможно записать уравнение прямой проходящей через две точки.
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать

Уравнение прямой в пространстве
Уравнение прямой, проходящей через две различные точки в пространстве
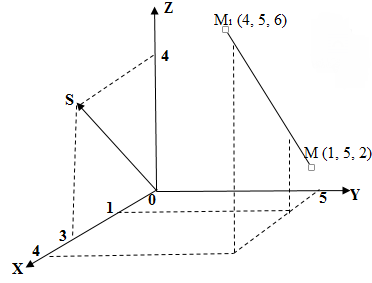
Если прямая проходит через две точки M( x 1, y 1, z 1) и N( x 2, y 2, z 2), такие что x 1 ≠ x 2, y 1 ≠ y 2 и z 1 ≠ z 2, то уравнение прямой можно найти используя следующую формулу
| x — x 1 | = | y — y 1 | = | z — z 1 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 |
Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
 | x = l t + x 0 |
| y = m t + y 0 | |
| z = n t + z 0 |
где ( x 0, y 0, z 0) — координаты точки лежащей на прямой, — координаты направляющего вектора прямой.
Каноническое уравнение прямой в пространстве
Если известны координаты точки M( x 0, y 0, z 0) лежащей на прямой и направляющего вектора n = , то уравнение прямой можно записать в каноническом виде, используя следующую формулу
| x — x 0 | = | y — y 0 | = | z — z 0 |
| l | m | n |
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
Видео:Направляющий и нормальный вектор прямой на плоскости | Векторная алгебраСкачать

Прямая в пространстве – виды уравнения прямой в пространстве
Прямая в пространстве – это линия, которая проходит от одной точки к другой, а также за пределы этих точек в бесконечность. Есть несколько видов уравнения прямой в пространстве: каноническое, параметрическое, угол между двумя прямыми в пространстве и т. д. Про это расскажем в данной статье и для наглядности предоставим несколько примеров.
Видео:Уравнения прямой на плоскости | Векторная алгебраСкачать

Параметрическое и каноническое уравнение прямой в пространстве
Параметрическое и каноническое уравнение прямой рассматривается практически так, как и для прямой на плоскости. Значит, нужно составить уравнение прямой , которая проходит через данную точку
параллельно направляющему вектору
.
Пусть, – произвольная точка прямой, тогда векторы
и
коллинеарные, а это значит, что координаты их пропорциональны, поэтому получаем:
это и есть канонические уравнения прямой.
Приравнивая каждую из дробей (1) к параметру , запишем параметрические уравнения прямой:
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнение прямой в пространстве, которая проходит через две заданные точки
Уравнение прямой в пространстве – тема очень лёгкая, так как здесь самое важное – знать нужную формулу. Тогда легко можно решить любую задачу.
Итак, через две точки и
можно не только геометрично провести линию, но и сложить её уравнения.
За направляющий вектор возьмём , тогда по формуле (1) у нас получается:
уравнение прямой в пространстве, которые проходят через две заданные точки.
Нужна помощь в написании работы?
Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Видео:Видеоурок "Общие уравнения прямой"Скачать

Общее уравнение прямой – переход к каноническому уравнению
Объяснение про общее уравнение прямой начнём с прямой, которая задана двумя плоскостями, что пересекаются по этой прямой.
Пусть известны их уравнения:
Тогда система (4) называется общим уравнением прямой.
Чтобы перейти к каноническим уравнениям вида (1), необходимо найти вектор и точку
этой прямой.
Точку находим, как один из решений системы (4). Например, положив в (4)
находим
, тогда и точку
. Направляющий вектор
, который параллелен к каждой из плоскостей
и
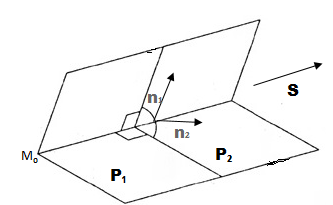
и перпендикулярен к их нормальным векторам
и
, то есть
,
. (см. рис. 1). Поэтому вектор
можно найти при помощи векторного произведения
и
=
x
=
Найдены координаты и
подставим в каноническое уравнение (1).
Например, от общих уравнений прямой:
Перейдём к каноническим, положив в системе (при нём относительно больше коэффициенты). найдём
. Нормальные векторы
и
. Тогда направляющий вектор
x
=
,
и канонические уравнения станут:
Видео:Лекция 28. Виды уравнения прямой в пространстве.Скачать

Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых
Угол между двумя прямыми :
и
равен углу между их направляющими векторами и
, поэтому
=
Условия параллельности и перпендикулярности прямых соответственно запишутся:
и
.
Видео:13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Примеры решения задач
Давайте рассмотрим первый пример, где можно двумя способами построить прямую:
Задача
При точке и направляющем векторе
необходимо:
- составить каноническое уравнение прямой;
- построить эту прямую.
Решение
1) По формуле (1) запишем каноническое уравнение прямой :
=
.
2) Рассмотрим два способа построения прямой .
Первый способ
В системе координат строим вектор
и точку
и проводим через точку
прямую параллельную вектору
.
Второй способ
По формуле (2) запишем каноническое уравнение прямой в параметрическом виде:
На рисунке видно, что при произвольных значениях из системы находим координаты соответствующих точек, которые принадлежат прямой
. Так при
находим координаты
. Через две точки
и
проводим прямую
.
Очевидно, что найти острый угол между прямыми совершенно не сложно при знании темы и определённых формул. Давайте разберём такой пример:
Задача
Найти острый угол между прямыми:
,
Решение
По формуле (7) получаем:
=
=
=
Так как , тогда угол
тупой,
, а острый угол
.
Ответ
.
Рассмотрим последний пример, где нужно составить уравнение. Здесь, как и в каждой задаче, важно знать и понимать, какой формулой нужно воспользоваться.
Задача
Составить уравнение прямой , которая проходит через точку
и параллельна прямой
.
Решение
От параметрического уравнения переходим к каноническому При условии параллельности прямых
то есть направляющим вектором новой прямой может служить известный вектор
и по формуле (1) у нас получается:
.
Ответ
.
🎥 Видео
Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

12. Уравнения прямой в пространстве Решение задачСкачать

Видеоурок "Нормальное уравнение прямой"Скачать

Видеоурок "Параметрические уравнения прямой"Скачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать