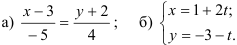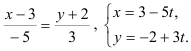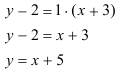Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Контрольная работа для студентов 1 курса по теме «Прямые и плоскости в пространстве».
Преподаватель математики Кисель Ольга Валерьевна ,
ГОБ ПОУ «Октябрьское техническое училище»
Отметка «5» выставляется, если студент набрал 25 – 30 баллов.
Отметка «4» выставляется, если студент набрал 21 – 24 балл.
Отметка «3» выставляется, если студент набрал 15 – 20 баллов.
Отметка «2» выставляется, если студент набрал менее 15 баллов.
«Прямые и плоскости в пространстве»
Параллельность прямых и плоскостей в пространстве
Часть 1. Задание с выбором ответа (1 балл).
А1. Какой плоскости не принадлежит точка А?
А2. На каких плоскостях лежит прямая DB?
А) АDC и ADB Б) ADB и ABC
С) ADB и DCB Д) DKB и DCA
A3. В какой точке пересекаются прямая PC и плоскость ADB?
A4.По какой прямой пересекаются плоскости AВС и ADC?
A5 .Какие прямые лежат в плоскости ABCD ?
А) DB , AC ,АА1 Б) NB , DA , CC 1
С ) DD1, DC,CA Д ) DB, DC, CA
А6. Укажите точку пересечения прямой MD с плоскостью ABC D
А) D Б) С С) А Д) M
А7 .Укажите прямую пересечения плоскостей АВС D и АВВ1 A 1
А) DВ Б) DС С) ВС Д) AВ
А8. Плоскости α и β пересекаются по прямой с. Выберите верную запись:
А) α × β= с Б) α ∩ β= с С) α ║ β= с Д) α ∩ β= С
А9. Туго натянутая нить закреплена в точках 1,2,3,4,5, расположенных на стержнях SA,SB,SC. Укажите количество точек в которых отрезки нити соприкасаются
А10.Как располагаются прямые AD1 и D1C1?
А) параллельны Б) пересекаются С) перпендикулярны
А11.Найдите угол между прямыми AD1 и ВВ1
А) 180º Б) 60 º С) 90 º Д) 45 º
А12. Найдите точку пересечения прямых DC и CC1
А) D Б) С С) А Д) К
А13. Найдите рёбра, параллельные грани АВВ1А1
Б) АВ, ВC, A 1 D 1, B 1 С 1 С) DD 1 , CC 1 , C 1 D 1, DС
Перпендикулярность прямых и плоскостей в пространстве
Часть 1. Задание с выбором ответа (1 балл).
А14.Укажите рёбра, перпендикулярные плоскости АВВ1А1
А) DА, ВC,СС 1 . AB 
А15. Выберите верное утверждение
А) AD║ BA Б) AB 

А16. Как расположены друг к другу рёбра куба, выходящие из одной вершины? А) Перпендикулярны Б) Параллельны
А17. Отрезок ВD перпендикулярен плоскости α. СD является: А) Перпендикуляром Б) Наклонной С) Проекцией наклонной
А18. Укажите общий перпендикуляр для прямых AD и CC1 А) DС Б) СА С) DD 1 Д) ВС
А19. Плоскости α и β параллельны. Каково взаимное расположение прямых AD и BC? А) Пересекаются Б) Скрещиваются
А20. Прямые a и b параллельные и лежат в плоскости α. Через каждую из этих прямых проведена плоскость, перпендикулярная α . Каково взаимное расположение полученных плоскостей?
А) Пересекаются Б) Скрещиваются С) Параллельны Д) Совпадают
Часть 2. Задание с развёрнутым ответом (2 балла).
В1. Даны две параллельные плоскости. Через точки А и В одной из плоскостей проведены две параллельные прямые до пересечения в точках А1 и В1. Найдите длину отрезка А1 В1 если АВ = 10 см.
В2. Две наклонные, проведённые из одной точки до пересечения с плоскостью, равны 15 и 20 см, проекция одного из отрезков равна 16 см. Найдите проекцию другого отрезка.
Часть 3. Задание с развёрнутым ответом (3 балла).
С1. Из точки О пересечения диагоналей квадрата АВСD к е го плоскости восстановлен перпендикуляр ОМ так, что 
С2. Из точки А построены три взаимно перпендикулярных отрезка АВ, АС и AD. Найдите длину отрезка СD если АС = а, ВС = в, ВD = с
«Прямые и плоскости в пространстве»
Параллельность прямых и плоскостей в пространстве
Часть 1. Задание с выбором ответа (1 балл).
А1. Какой плоскости не принадлежит точка В?
А2.На каких плоскостях лежит прямая DА?
А) АDC и ADB Б) ADB и ABC С) ADB и DCB Д) DKB и DCA
A3. В какой точке пересекаются прямая DК и плоскость ADB? А) Р Б) К С) А Д) D
A4. По какой прямой пересекаются плоскости AВС и ADВ? А) DВ Б) DС С) АС Д) ВA
A5. Какие прямые лежат в плоскости BDА?
А ) DB, AC,DK. AB Б ) KB, DA,DK. CP
С) DP, DВ,DА. ВA Д) DB, DC,DK. CB
А7. Укажите прямую пересечения плоскостей АВD и АDD 1
А) DВ Б) ВВ 1 С) ВС Д) AD
А8. Прямые а и b пересекаются в точке С. Выберите верную запись:
А) a ×b= с Б) a ∩ b= с С) a║ b= с Д) a∩ b= С
А9. Туго натянутая нить закреплена в точках 1,2,3,4,5, 6 расположенных на стержнях SA,SB,SC. Укажите количество точек в которых отрезки нити соприкасаются

А) параллельны Б) пересекаются С) перпендикулярны
А11. Найдите угол между прямыми AА 1 и ВС
А) 180º Б) 60 º С) 90 º Д) 45 º
А12. Найдите точку пересечения прямых DC и D 1 P
А) D Б) С С) А Д) К
А) ВС, CC 1 , ВВ 1, B 1 С 1 Б) АВ, ВC, A 1 D 1, B 1 С 1
Перпендикулярность прямых и плоскостей в пространстве
Часть 1. Задание с выбором ответа (1 балл).
А14. Укажите рёбра, перпендикулярные плоскости АВС D
А15. Выберите верное утверждение
А) AD 


А16. Можно ли провести плоскость через четыре произвольные точки пространства?
А17. Отрезок ВD перпендикулярен плоскости α. СВ является:
А) Перпендикуляром В) Наклонной
С) Проекцией наклонной
А18. Укажите общий перпендикуляр для прямых AВ и CC 1 А) DС В) СА С) DD 1 Д) ВС
А19. Плоскости α и β параллельны. Каково взаимное расположение прямых AС и BD?
А) Параллельны В) Скрещиваются
А20. Прямые a и b-скрещивающиеся.Через а проведена плоскость α ║ b,. Через прямую b проведена плоскость β║а, . Каково взаимное расположение плоскостей α и β?
А) Пересекаются В) Скрещиваются С) Параллельны Д) Совпадают
Часть 2. Задание с развёрнутым ответом (2 балла).
В1. Даны две параллельные плоскости. Через точки А и В одной из плоскостей проведены две параллельные прямые до пересечения в точках А 1 и В 1 . Найдите длину отрезка АА 1 если ВВ 1 = 16 см.
В2. Д ве наклонные, проведённые из одной точки до пересечения с плоскостью, равны 7 и 10 см, проекция одного из отрезков равна 8 см. Найдите проекцию другого отрезка.
Часть 3. Задание с развёрнутым ответом (3 балла).
С1. Из точки О пересечения диагоналей квадрата АВСD к е го плоскости восстановлен перпендикуляр ОМ так, что 
С2. Из точки А построены три взаимно перпендикулярных отрезка АВ, АС и AD. Найдите длину отрезка ВD если АС = а, ВС = в, СD = с
«Прямые и плоскости в пространстве»
Параллельность прямых и плоскостей в пространстве
Часть 1. Задание с выбором ответа (1 балл).
А1. Какой плоскости не принадлежит точка С? А) РDВ Б) АDС С) АРС Д) ВDС
А2. На каких плоскостях лежит прямая DС?
А) АDC и ADB Б) ADB и ABC С) ADB и DCB Д) DСB и DCA
A3. В какой точке пересекаются прямая DМ и плоскость AСB?
А) Р Б) С С) А Д) D
A4. По какой прямой пересекаются плоскости AВС и ВDC?
А) DВ Б) ВС С) АС Д) ВA
A5. Какие прямые лежат в плоскости BАC?
А) АB, AC,СР. СB Б) KB, DA,DK. CP С) DP, DC,DK. CA Д) DB, DC,DK. CB
А7. Укажите прямую пересечения плоскостей АВС и DСС 1
А) DВ Б) DС С) ВС Д) AВ
А8. Плоскости α и β пересекаются по прямой b. Выберите верную запись:
А) α × β= b Б) α ∩ β= B С) α ║ β= b Д) α ∩ β= b
А9. Туго натянутая нить закреплена в точках 1,2,3,4,5, 6 расположенных на стержнях a,b,c. Укажите количество точек в которых отрезки нити соприкасаются

А) параллельны Б) скрещиваются С) перпендикулярны
А) 180º Б) 60 º С) 90 º Д) 45 º
А12. Найдите точку пересечения прямых DА и АА 1
А) D Б) С С) А Д) К
А13. Найдите рёбра, параллельные грани АВСD
А) АD, ВC, A 1 D 1, B 1 С 1 Б) АВ, ВC, A 1 D 1, B 1 С 1
Перпендикулярность прямых и плоскостей в пространстве
Часть 1. Задание с выбором ответа (1 балл).
А15. Выберите верное утверждение
А) AD║ DC Б) AB 

А16. Две точки круга лежат в плоскости. Лежит ли весь круг в этой плоскости? А)Нет Б) Да
А17. Отрезок ВD перпендикулярен плоскости α. ВD является: А) Перпендикуляром Б) Наклонной С) Проекцией наклонной
А18. Укажите общий перпендикуляр для прямых СD и ВВ 1
А) DС Б) СА С) DD 1 Д) ВС
А19. Отрезки АВ и СD лежат в плоскостях α и β. Прямые АС и ВD параллельны. Каково взаимное расположение плоскостей α и β?
А) Пересекаются Б) Параллельны
А20. Три луча АВ, АС, АК попарно перпендикулярны. Как расположен каждый из лучей по отношению плоскости, определяемой двумя другими лучами.
А) Перпендикулярен Б) Скрещивается С) Параллелен Д) Совпадает
Часть 2. Задание с развёрнутым ответом (2 балла).
В1 Даны две параллельные плоскости. Через точки А и В одной из плоскостей проведены две параллельные прямые до пересечения в точках А 1 и В 1 . Найдите длину отрезка АВ если А 1 В 1 = 3 см.
В2. Две наклонные, проведённые из одной точки до пересечения с плоскостью, равны 4 и 5 см, проекция одного из отрезков равна 4 см. Найдите проекцию другого отрезка.
Часть 3. Задание с развёрнутым ответом (3 балла).
С1. Из точки О пересечения диагоналей квадрата АВСD к е го плоскости восстановлен перпендикуляр ОМ так, что 
С2. Из точки А построены три взаимно перпендикулярных отрезка АВ, АС и AD. Найдите длину отрезка СD если АС = 3 см, ВС = 4 см, ВD = 5 см
Видео:Уравнение прямой в пространстве. 11 класс.Скачать

Контрольная работа на тему: прямая на плоскости, кривые второго порядка
Прямая на плоскости. Кривые второго порядка
Задание: Составление уравнений прямых.
Цель: формирование умения составлять уравнения прямых на плоскости.
Задание для самостоятельной внеаудиторной работы:
7.1. Опираясь на обобщающие таблицы, изучите, какими способами можно задать прямую, и какие виды уравнения прямой существуют.
7.2. В треугольнике 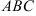
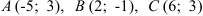
а) прямой 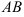
б) медианы 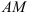
в) прямой, проходящей через точку 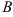
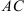
г) прямой, проходящей через точку 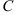
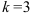
7.3. 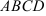
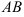
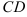
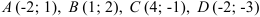
а) диагонали 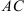
б) прямой, параллельной основаниям, проходящей через точку 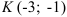
в) прямой, проходящей через точку 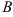
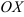
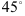
г) средней линии трапеции в каноническом виде;
д) прямой, проходящей через точку 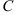
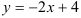
7.4. Запишите уравнение прямой во всех видах (общем, каноническом, параметрическом, с угловым коэффициентом) и постройте эту прямую:
Методические указания по выполнению работы:
Уравнением линии на плоскости называется уравнение с двумя переменными 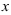
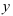
Прямые — самые простые линии на плоскости. Им соответствуют уравнения первой степени.
При решении задач удобно использовать следующие обобщающие таблицы:
Способы задания прямой

Виды уравнений прямой
Рассмотрим примеры решения типовых задач.
Пример 1.
Составьте уравнение прямой, проходящей через точку 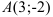
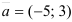
Решение:
Определим способ задания прямой: с помощью точки 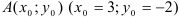
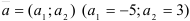
Подставим координаты точки и направляющего вектора в уравнение 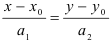
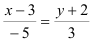
Подставим координаты точки и направляющего вектора в уравнение
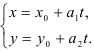
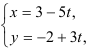
Ответ:
Пример 2.
Составьте уравнение прямой, проходящей через точки 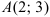
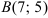
Решение:
Подставив в формулу 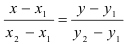
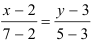
Ответ: 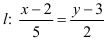
Пример 3.
Составьте уравнение прямой, проходящей через точку 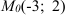
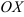
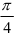
Решение:
Найдём угловой коэффициент прямой: 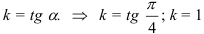
Подставим 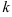
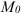
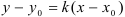
Ответ: 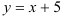
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:11. Прямая в пространстве и ее уравненияСкачать

Тест «Прямые и плоскости в пространстве»
Видео:Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Методички Педсовета
08 апреля 2021 • 13:56
Раздел «Прямые и плоскости в пространстве» занимает важное место в стереометрии. Тест дает возможность определить уровень усвоения материала и быстро выявить пробелы в знаниях, создает условия для мотивации, повышения интереса к предмету, способствует развитию и совершенствованию самостоятельной деятельности учащихся и устраняет перегрузку домашнего задания.
1) Прямую, перпендикулярную любой прямой в плоскости, называют…
а) наклонной к плоскости;
б) перпендикуляром к плоскости;
в) секущей;
г) лучом.
2) Наклонной к плоскости называют прямую, пересекающую плоскость и…
а) не пересекающую перпендикуляр;
б) лежащую в ней;
в) не имеющую с ней общих точек;
г) не перпендикулярную ей.
3) Параллельными называют плоскости,…
а) не имеющие общих прямых;
б) у которых одна общая точка;
в) у которых две общих точки;
г) не имеющие ни одной общей точки.
4) Прямая, проходящая через основания перпендикуляра и наклонной, называется…
а) секущей;
б) параллельной плоскости;
в) проекцией наклонной на плоскость;
г) перпендикуляром к плоскости.
5) Наклонная перпендикулярна прямой в плоскости, если…
а) перпендикуляр пересекается с проекцией наклонной на плоскость;
б) проекция наклонной параллельна этой прямой;
в) проекция наклонной перпендикулярна этой прямой;
г) прямая совпадает с проекцией наклонной.
6) Если из точки вне плоскости провести к ней перпендикуляр и наклонные, то…
а) перпендикуляр длиннее наклонной;
б) наклонная длиннее перпендикуляра;
в) проекция наклонной короче перпендикуляра;
г) наклонная и ее проекция равны.
7) Прямая параллельна плоскости, если они…
а) пересекают прямую в одной и той же точке;
б) перпендикулярны одной и той же прямой;
в) удалены от данной точки на равные расстояния;
г) пересекают плоскость в одной точке.
8) Углом между наклонной и плоскостью называют…
а) угол между наклонной и перпендикуляром;
б) угол между проекцией и перпендикуляром;
в) угол между наклонной и ее проекцией;
г) угол между наклонной и прямой в плоскости.
9) Через… проходит единственная плоскость,
а) две точки;
б) три параллельные прямые;
в) три попарно пересекающиеся прямые;
г) четыре точки.
10) Прямая пересекает плоскость, если прямая и плоскость. . .
а) не имеют ни одной общей точки;
б) имеют две общие точки;
в) имеют только одну общую точку;
г) имеют три общих точки.
11) Если прямая пересекает плоскость квадрата в точке пересечения диагоналей и перпендикулярна двум смежным его сторонам, то она. . .
а) параллельна двум другим сторонам квадрата;
б) перпендикулярна диагоналям квадрата;
в) параллельна диагоналям квадрата;
г) образует с плоскостью квадрата угол в 30 градусов.
12) Если две параллельные плоскости пересечь третьей, то. . .
а) линии пересечения равны;
б) линии пересечения параллельны;
в) линии пересечения перпендикулярны;
г) плоскости совпадают.
13) Если две параллельные плоскости пересечь двумя параллельными прямыми, то…
а) прямые пересекаются в точке;
б) плоскости пересекаются по прямой, параллельной одной из прямых;
в) отрезки, заключенные между плоскостями равны;
г) плоскости перпендикулярны одной из прямых.
14) Если наклонная длиной 16 см образует с плоскостью угол в 60°, то ее проекция на плоскость равна…
а) 32 см;
б) 8 см;
в) 8 cm;
г) 256 см².
15) Наклонные АВ и АС образуют с плоскостью углы в 30° и 45° соответственно. Тогда. . .
а) проекция наклонной АВ длиннее проекции наклонной АС на плоскость;
б) наклонная АВ короче наклонной АС;
в) наклонная АВ длиннее наклонной АС;
г) проекции наклонных равны.
16) Если в прямоугольном треугольнике катет в два раза меньше гипотенузы, то…
а) прилежащий катету угол равен 30 градусам;
б) прилежащий катету угол равен 60 градусам;
в) прилежащий катету угол равен 90 градусам;
г) противолежащий угол равен 60 градусам.
17) Перпендикуляром к-плоскости называют прямую, . . .
а) пересекающую плоскость;
б) перпендикулярную некоторой прямой в плоскости;
в) перпендикулярную любой прямой в плоскости;
г) лежащую в параллельной плоскости.
18) Та из наклонных больше, у которой. . .
а) проекция равна перпендикуляру;
б) проекция больше;
в) проекция меньше;
г) проекция больше перпендикуляра.
19) Планиметрия — это измерения. . .
а) углов;
б) отрезков;
в) на плоскости;
г) в пространстве.
20) Угол между наклонной и плоскостью. . .
а) меньше 90 градусов;
б) больше 90 градусов;
в) равен 60 градусам;
г) тупой.
21) Проекцией наклонной на плоскость называют прямую, . . .
а) перпендикулярную плоскости;
б) пересекающую наклонную под углом 30 градусов;
в) проходящую через точки наклонной и перпендикуляра;
г) проходящую через основания наклонной и перпендикуляра.
22) Если две точки прямой принадлежат плоскости, то прямая…
а) называется проекцией точки на плоскость;
б) лежит в плоскости;
в) пересекает плоскость под прямым углом;
г) называется перпендикуляром к плоскости.
23) Прямые, имеющие одну общую точку называют. . .
а) скрещивающимися;
б) пересекающимися;
в) параллельными;
г) совпадающими.
24) Две плоскости параллельны, если они. . .
а) перпендикулярны одной и той же прямой;
б) параллельны одной и той же прямой;
в) пересекаются в одной точке;
г) пересекают одну и ту же прямую.
25) Если две прямые параллельны третьей, то они.
а) перпендикулярны друг другу;
б) параллельны между собой;
в) совпадают;
г) пересекаются.
26) Расстояние между двумя параллельными плоскостями равно 10 см, а отрезок, заключенный между плоскостями равен 12 см. Тогда проекция отрезка на одну из плоскостей равна…
a) см;
б) 44 см;
в) см;
г) 2 см.
27) Две наклонные, длиной 10 см образуют между собой угол в 60 градусов. Расстояние между их проекциями на плоскость равно…
а) 10 см;
б) 5 см;
в) см;
г) 20 см.
28) Две плоскости совпадают, если они имеют. . .
а) две общих точки;
б) три общих точки;
в) одну общую прямую;
г) одну общую точку.
(2 балла)
Видео:Лекция 28. Виды уравнения прямой в пространстве.Скачать

Ответы:
1-б, 2-г, 3-г, 4-в, 5-в, 6-б, 7-б, 8-в, 9-в, 10-в, 11-б, 12-б, 13-в, 14-б, 15-а, в,
16-б, 17-в, 18-б, 19-в, 20-а, 21-г, 22-б, 23-б, 24-а, 25-б, 26-а, 27-а, 28-б.
📺 Видео
Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать

Семинар №5 Контрольная работа 1Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Видеоурок "Общие уравнения прямой"Скачать

Видеоурок "Канонические уравнения прямой"Скачать

Уравнение прямой по двум точкамСкачать

Каноническое уравнение прямой в пространстве. 11 класс.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Написать канонические и параметрические уравнения прямой в пространствеСкачать

Уравнения прямой на плоскости | Векторная алгебраСкачать

Математика это не ИсламСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать