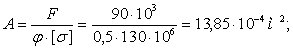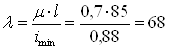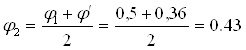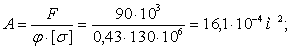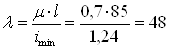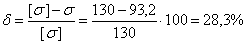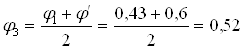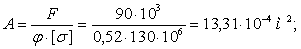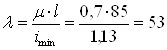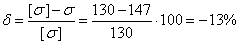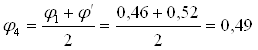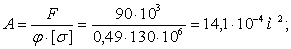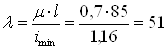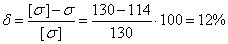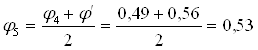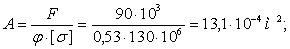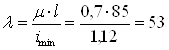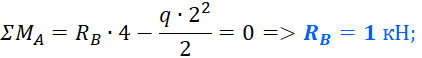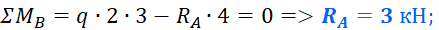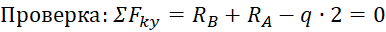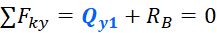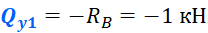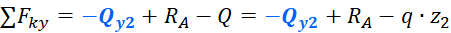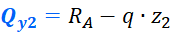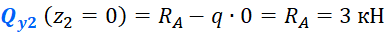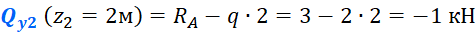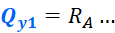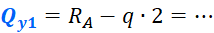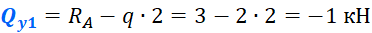Про уравнения - легко » Статьи

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Обновлено
Содержание
  1. iSopromat.ru
  2. Эпюры при чистом изгибе
  3. Эпюры при поперечном изгибе
  4. Геометрическая проверка эпюр
  5. Эпюры для двухопорных балок
  6. Запишем уравнения поперечных сил и изгибающих моментов для каждого участка балки
  7. Эпюра поперечных сил — как построить?
  8. Подробный способ построения эпюры поперечных сил
  9. Разбиваем балку на участки
  10. Метод сечений
  11. Правила знаков для поперечной силы
  12. Вводим систему координат для первого участка
  13. Записываем уравнение равновесия для первого участка и строим эпюру
  14. Расчет второго участка
  15. Упрощенный способ построения эпюры
  16. Первый участок
  17. Второй участок
  18. Быстрый способ построения эпюры
  19. 📹 Видео

Видео:Построение эпюр в балке ( Q и M ). СопроматСкачать

Построение эпюр в балке ( Q и M ). Сопромат

iSopromat.ru

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Эпюрами внутренних поперечных сил и изгибающих моментов называют графическое представление распределения функций Q и M по длине балки при изгибе.

Эпюры строятся для визуального представления распределения внутренних силовых факторов и определения опасных (т.е. наиболее нагруженных) с точки зрения прочности участков бруса.

Рассмотрим некоторые примеры на построение эпюр в балках:

Видео:ЗАПОМНИ ТРИ ГЛАВНЫХ ПРАВИЛА и ты сможешь удивить своего препода по сопромату!Скачать

ЗАПОМНИ ТРИ ГЛАВНЫХ ПРАВИЛА и ты сможешь удивить своего препода по сопромату!

Эпюры при чистом изгибе

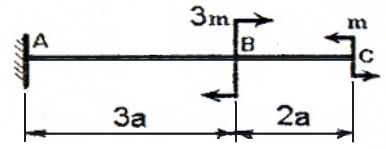
Для консольной балки:
Уравнения поперечных сил и изгибающих моментов для каждого участка балки

имеем два силовых участка (AB и BC) и на каждом из них, применяя метод сечений, будем рассматривать, например правую от сечения часть, используя формулы и правило знаков для расчета внутренних силовых факторов.

Отсчет координаты z можно вести от единого начала координат или для каждого силового участка в отдельности.
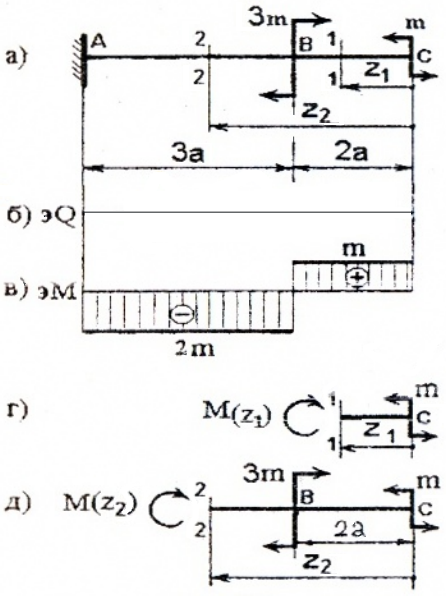
I силовой участок (BC): 0 ≥ z1 ≥ 2a (рис. 2 а,г)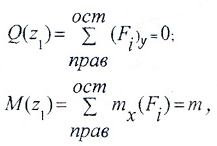
Уравнения поперечных сил и изгибающих моментов для каждого участка балки
Уравнения поперечных сил и изгибающих моментов для каждого участка балки

т.е. Q(z1)=0 на всем участке, а M(z1)=m=const.
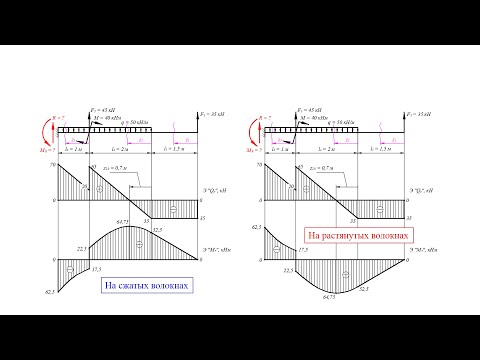
Ординаты эпюр Q и M со знаком плюс (+) будем откладывать вверх от нулевой (базовой) линии, при этом эпюру M будем строить на сжатых волокнах.

II силовой участок (AB): 2a ≥ z2 ≥ 5a (рис. 2 а,д)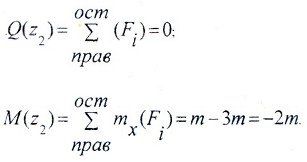
Уравнения поперечных сил и изгибающих моментов для каждого участка балки
Откладывая на границах участков в сечениях C, B и A значения полученных ординат Q и M, строим эпюры (рис. 2 б, в).

Более нагруженным оказался участок AB, он и является опасным: Mmax=|2m|.
Так как поперечные силы Q по всей длине балки равны нулю, балка испытывает чистый изгиб.

Видео:БАЛКА - 90 СТУДЕНТОВ САМОСТОЯТЕЛЬНО СТРОЯТ ЭПЮРЫ после просмотра этого видео!Скачать

БАЛКА - 90 СТУДЕНТОВ САМОСТОЯТЕЛЬНО СТРОЯТ ЭПЮРЫ после просмотра этого видео!

Эпюры при поперечном изгибе

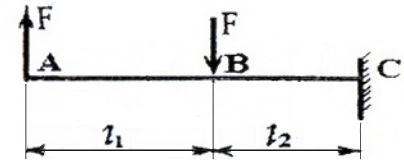
Построение эпюр Q и M для балки, изображенной на рис. 3
Уравнения поперечных сил и изгибающих моментов для каждого участка балки

проводим аналогично, но рассматривать будем левые от сечений части, т.к. в правые войдут реакции в заделке, что несколько усложняет вычисления.

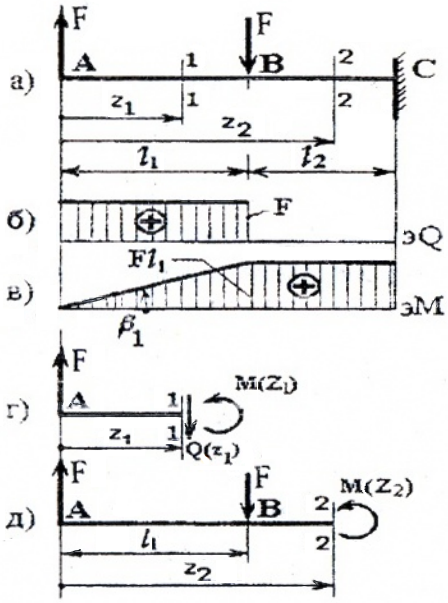
I силовой участок (AB): 0 ≥ z1 ≥ l1 (рис. 4, а, г)
Q(z1)= F=const, на всем участке постоянная величина,
M(z1)=F×z1, уравнение прямой, график строим по двум граничным точкам:
M(z1=0)=F×0=0 – в сечении A;
M(z1=l1)=F× l1 — в сечении B.
Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Опасным является сечение B, в котором действуют Qmax=F, Mmax=Fl1.

Геометрическая проверка эпюр

Геометрическая проверка правильности построения эпюр Q и M по дифференциальным зависимостям заключается в следующем:
Для всех силовых участков находим: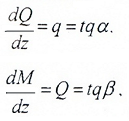
Уравнения поперечных сил и изгибающих моментов для каждого участка балки
где α, β – углы наклона касательных к эпюрам Q и M относительно оси абсцисс (базовой линии).
На участке “AB” α1=0 (линия эпюры Q горизонтальна), следовательно,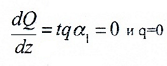
Уравнения поперечных сил и изгибающих моментов для каждого участка балки
распределенная нагрузка отсутствует;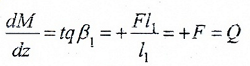
Уравнения поперечных сил и изгибающих моментов для каждого участка балки
функция M (z1) – возрастающая.

На участке “BC”: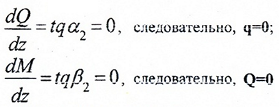
Уравнения поперечных сил и изгибающих моментов для каждого участка балки
Так как все дифференциальные проверки выполняются, эпюры построены верно.

Видео:Построение эпюр изгибающих моментов M и поперечных сил Q в балкеСкачать

Построение эпюр изгибающих моментов M и поперечных сил Q в балке

Эпюры для двухопорных балок

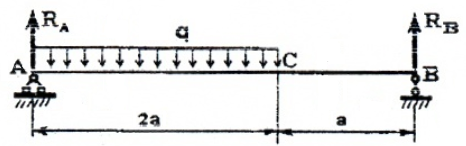
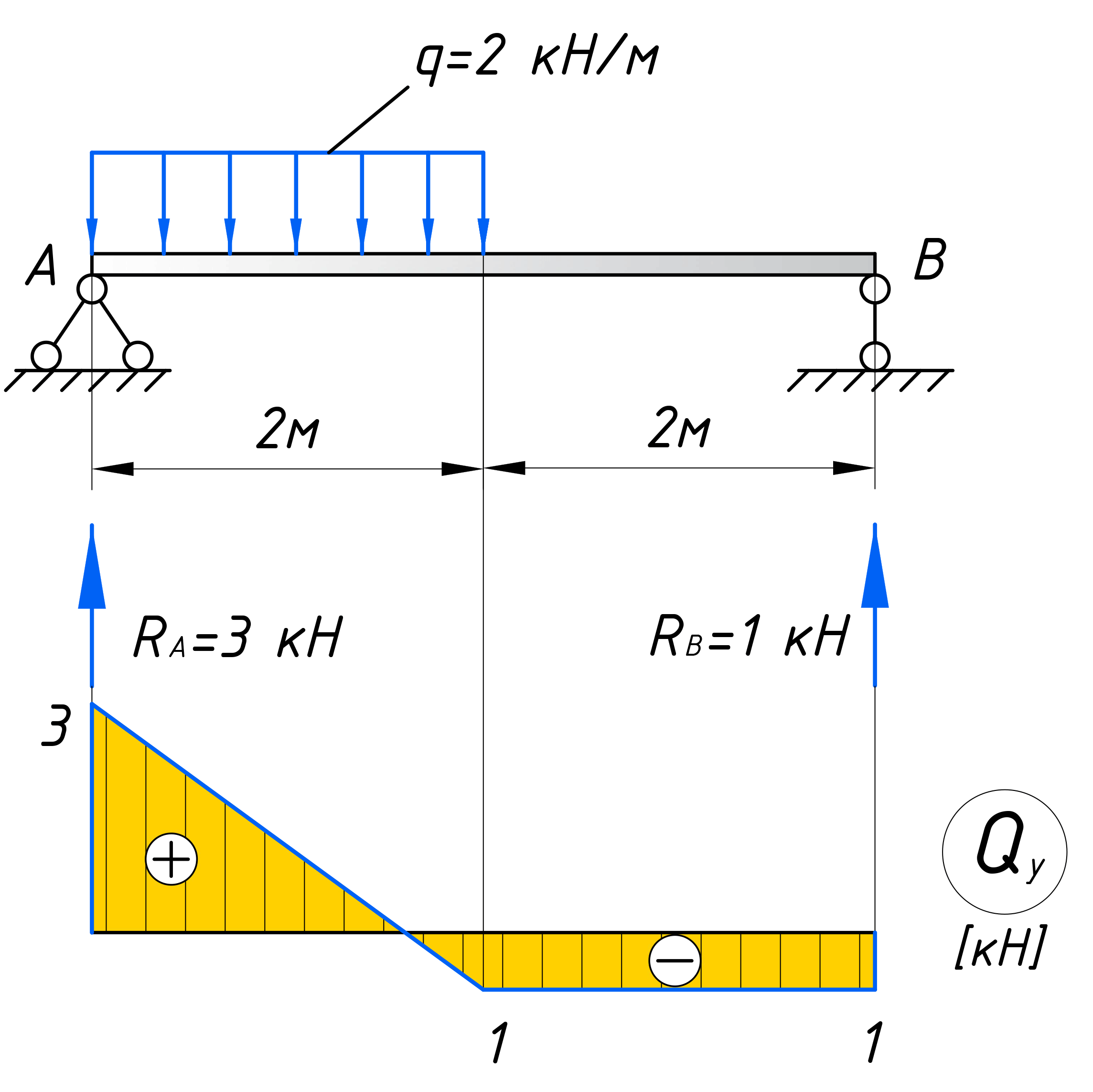
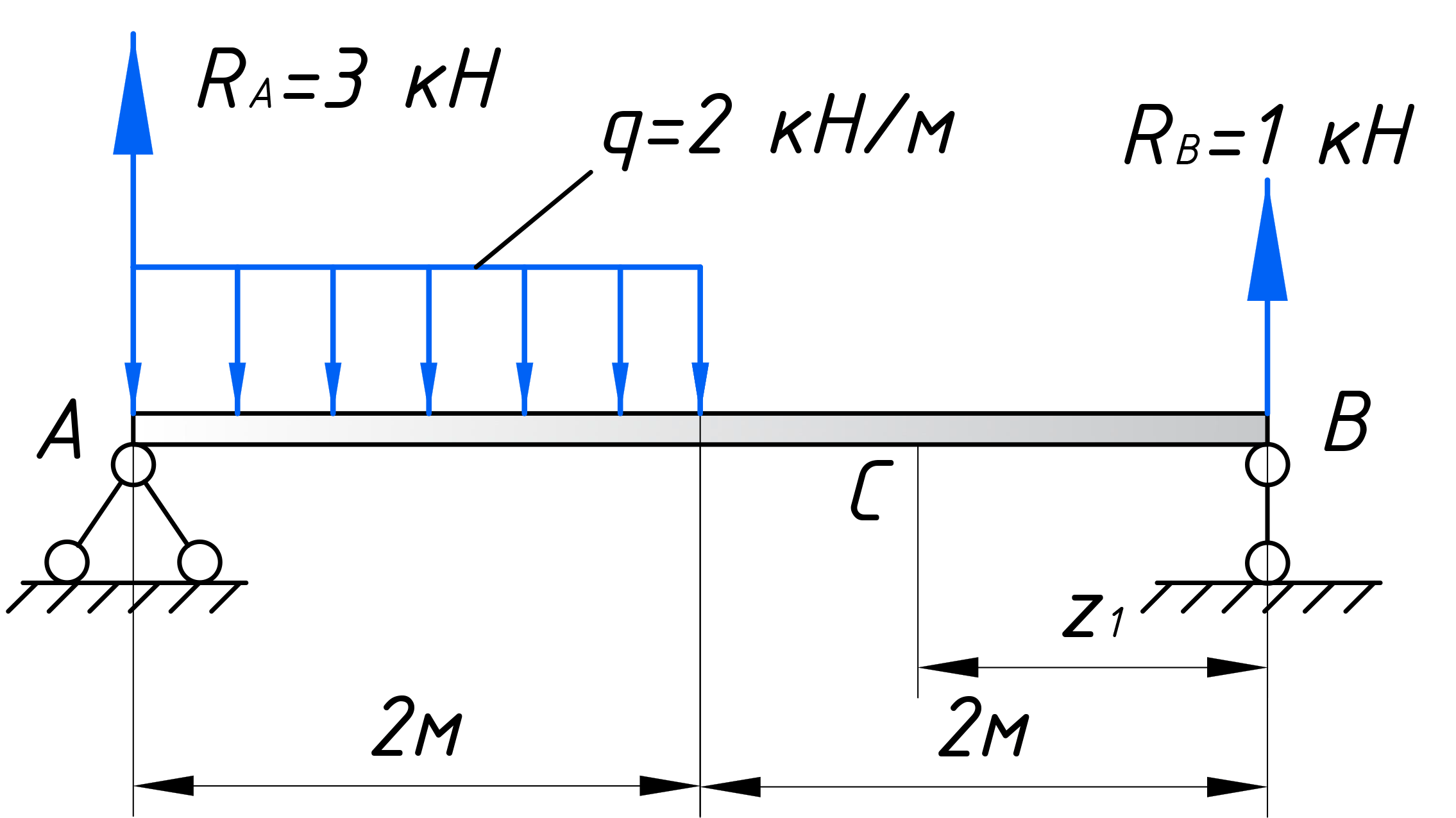
Рассматривая расчетные схемы такого типа, как двухопорная балка (рис. 5),
Уравнения поперечных сил и изгибающих моментов для каждого участка балки

необходимо вначале найти опорные реакции и только потом строить эпюры.

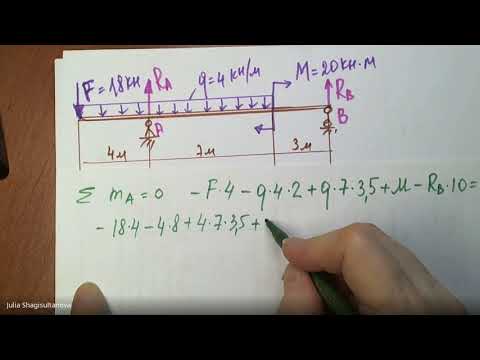
Обычно, рекомендуется использовать суммы моментов вокруг опорных точек, например: ∑MA=0 и ∑MB=0.

Записываем уравнения и находим значения реакций: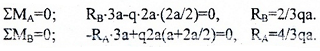
Уравнения поперечных сил и изгибающих моментов для каждого участка балки
Чтобы убедиться в правильности полученных значений необходимо провести «арифметическую проверку» тождества по оставшемуся из зависимых уравнений: ∑FY=0 или ∑MС=0.

Проверим через сумму сил, приложенных к балке (включая найденные опорные реакции). Она должна равняться нулю (при округлении значений, может появиться погрешность).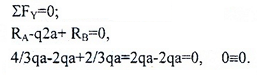
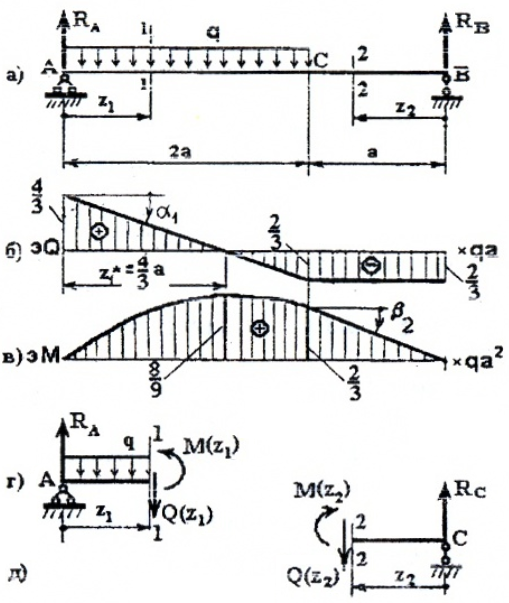
Уравнения поперечных сил и изгибающих моментов для каждого участка балки
Для построения эпюр рассмотрим два силовых участка:
Уравнения поперечных сил и изгибающих моментов для каждого участка балки

I участок (AC): 0 ≥ z1 ≥2a (рис. 6, а, г)
Q(z1)=RA-qz1 — прямая, которую строим по двум граничным точкам: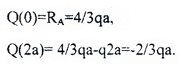
Уравнения поперечных сил и изгибающих моментов для каждого участка балки
M(z1)=RAz1-qz1(z1/2)= RAz1-qz1 2 /2 – парабола.

Строим эту кривую по трем точкам: по двум граничным (0 и 2a) и z*, которая соответствует Mmax(z*), и дифференциальной зависимости: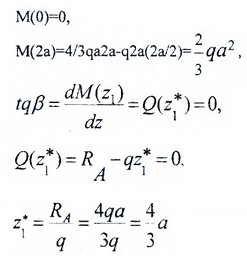
Уравнения поперечных сил и изгибающих моментов для каждого участка балки
Определяем экстремум эпюры M на участке: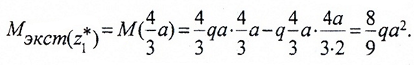
Уравнения поперечных сил и изгибающих моментов для каждого участка балки
II участок (BC): 0 ≥ z2 ≥ a (рис. 6, а, д)
Q(z2)= -RB= -2/3qa;
M(z2)=RBz2,
M(z2=0)=0,
M(z2=a)=2/3qa 2 .
Выполним проверку дифференциальных зависимостей.
I силовой участок: 0 ≥ z1 ≥ 2a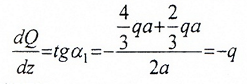
Уравнения поперечных сил и изгибающих моментов для каждого участка балки
— направлена вниз, функция Q(z1) – убывающая.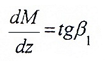
Уравнения поперечных сил и изгибающих моментов для каждого участка балки
— проверка визуально: чем больше угол наклона β1, тем больше значение Q(z1).

II силовой участок: 0 ≥ z2 ≥ a.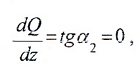
Уравнения поперечных сил и изгибающих моментов для каждого участка балки
следовательно, q=0.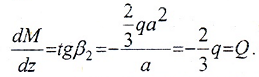
Уравнения поперечных сил и изгибающих моментов для каждого участка балки
функция M(z) – убывающая.
Все проверки выполнены, следовательно, эпюры построены верно.
По эпюрам видно, что опасных сечений два (рис. 6):
По моменту при z1*=4/3a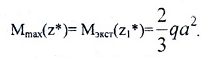
Уравнения поперечных сил и изгибающих моментов для каждого участка балки
По силе в сечении «A»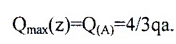
Уравнения поперечных сил и изгибающих моментов для каждого участка балки
После построения и проверки эпюр можно приступать к расчетам балки на прочность и жесткость.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Построение эпюр поперечных сил и изгибающих моментов в многопролетных шарнирно-консольных балках.Скачать

Построение эпюр поперечных сил и изгибающих моментов в многопролетных шарнирно-консольных балках.

Запишем уравнения поперечных сил и изгибающих моментов для каждого участка балки

2. Запишем уравнения поперечных сил и изгибающих моментов для каждого участка балки.

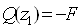
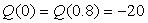
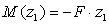
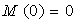
Уравнения поперечных сил и изгибающих моментов для каждого участка балки; Уравнения поперечных сил и изгибающих моментов для каждого участка балкикН;

Уравнения поперечных сил и изгибающих моментов для каждого участка балки; Уравнения поперечных сил и изгибающих моментов для каждого участка балки; Уравнения поперечных сил и изгибающих моментов для каждого участка балкикНм.

Строим эпюры по вычисленным значениям.

3.1. Двутавровое поперечное сечение.

Этому моменту сопротивления соответствует двутавр №24, момент сопротивления и площадь поперечного сечения которого соответственно равны Wx=289 cм 3 ; А= 34,8 см 2 .

3.2. Прямоугольное сечение (h/b = 2).

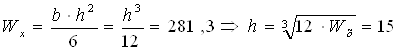
Уравнения поперечных сил и изгибающих моментов для каждого участка балкисм

h=15 см; b=7,5 см; А=112,5 см 2 .

3.3. Круглое поперечное сечение:

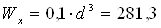
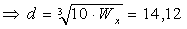
Уравнения поперечных сил и изгибающих моментов для каждого участка балки, Уравнения поперечных сил и изгибающих моментов для каждого участка балкисм

Уравнения поперечных сил и изгибающих моментов для каждого участка балкисм 2 .

3.4. Кольцевое сечение (с = 0,7).

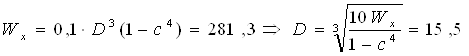
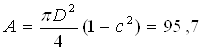
Уравнения поперечных сил и изгибающих моментов для каждого участка балкисм

Уравнения поперечных сил и изгибающих моментов для каждого участка балкисм 2

3. Сравниваем площади поперечных сечений А, подобранных профилей, сведя данные в Таблицу 2:

Площадь сечения, см 2

Тип сечения
Двутавровое38,4
Прямоугольное112,5
Круглое156,4
Кольцевое95,7

Таким образом, при изгибе оптимальным является сечение двутавра.

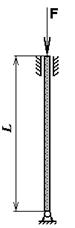
Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Дан стержень с опорами, закрепленными по указанной схеме, сжат силой F = 90 кН. Поперечное сечение – равносторонний треугольник. Длина стержня 1 = 0,85 м. Материал стержня — чугун. Модуль упругости Е = 1,3×10 5 МПа, допускаемое напряжение [σ] = 130 МПа. Коэффициент закрепления опор m = 0,7

— размеры поперечного сечения при допускаемом напряжении на сжатие [σ];

— величину критической силы Fk;

— коэффициент запаса устойчивости nу.

Задача решается методом приближения. В первом приближении задаемся коэффициентом уменьшения основного допускаемого напряжения j1 = 0,5. Из условия устойчивости определяем площадь сечения:

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Из площади сечения находим сторону сечения b:

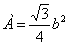
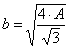
Уравнения поперечных сил и изгибающих моментов для каждого участка балкиÞ Уравнения поперечных сил и изгибающих моментов для каждого участка балки= 4,3 см.

Определяем минимальный радиус инерции по формуле:

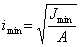
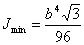
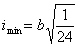
Уравнения поперечных сил и изгибающих моментов для каждого участка балки, где Уравнения поперечных сил и изгибающих моментов для каждого участка балки.

Уравнения поперечных сил и изгибающих моментов для каждого участка балки=0,88 см

Определяем гибкость стержня:

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

По таблице находим соответствующее значение коэффициента уменьшения основного допускаемого напряжения j’ = 0,36. Производим проверку на устойчивость:

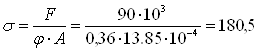
Уравнения поперечных сил и изгибающих моментов для каждого участка балкиМПа > [s]

Так как σ > [σ], то задаемся новым значением φ и повторяем весь расчет.

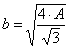
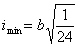
Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Уравнения поперечных сил и изгибающих моментов для каждого участка балки=6,1 см. Уравнения поперечных сил и изгибающих моментов для каждого участка балки= 1,24 см.

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

По таблице находим соответствующее значение коэффициента уменьшения основного допускаемого напряжения j’ = 0,6. Производим проверку на устойчивость:

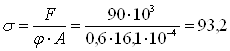
Уравнения поперечных сил и изгибающих моментов для каждого участка балкиМПа

Допускаемая погрешность не более 5%. Определяем погрешность

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Погрешность больше допустимой, поэтому задаемся новым значением φ и повторяем весь расчет.

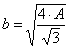
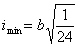
Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Уравнения поперечных сил и изгибающих моментов для каждого участка балки=5,54 см. Уравнения поперечных сил и изгибающих моментов для каждого участка балки= 1,13 см.

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

По таблице находим соответствующее значение коэффициента уменьшения основного допускаемого напряжения j’ = 0,46. Производим проверку на устойчивость:

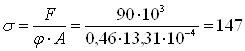
Уравнения поперечных сил и изгибающих моментов для каждого участка балкиМПа

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Погрешность не находится в допускаемых пределах.

Задаемся новым значением φ и повторяем весь расчет.

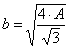
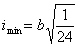
Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Уравнения поперечных сил и изгибающих моментов для каждого участка балки=5,71 см. Уравнения поперечных сил и изгибающих моментов для каждого участка балки= 1,16 см.

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

По таблице находим соответствующее значение коэффициента уменьшения основного допускаемого напряжения j’ = 0,56. Производим проверку на устойчивость:

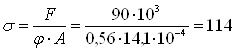
Уравнения поперечных сил и изгибающих моментов для каждого участка балкиМПа

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Погрешность не находится в допускаемых пределах.

Задаемся новым значением φ и повторяем весь расчет.

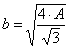
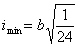
Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Уравнения поперечных сил и изгибающих моментов для каждого участка балки=5,5 см. Уравнения поперечных сил и изгибающих моментов для каждого участка балки= 1,12 см.

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

По таблице находим соответствующее значение коэффициента уменьшения основного допускаемого напряжения j’ = 0,46. Производим проверку на устойчивость:

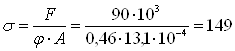
Уравнения поперечных сил и изгибающих моментов для каждого участка балкиМПа

Значения повторяются. Поэтому принимаем b = 5,71 см, А = 14,1 см 2 .

Определяем критическую силу:

Уравнения поперечных сил и изгибающих моментов для каждого участка балкикН.

Определяем коэффициент запаса устойчивости:

Видео:Построение эпюр поперечных сил и изгибающих моментов в балке.Скачать

Построение эпюр поперечных сил и изгибающих моментов в балке.

Эпюра поперечных сил — как построить?

Привет! Сегодня будем учиться строить эпюры поперечных сил. В этой статье я расскажу, что такое поперечная сила, чем интересна и полезна при проведении расчетов на прочность и жесткость. По уже сложившейся традиции, как и с другими эпюрами, будем рассматривать три способа построения эпюры поперечных сил: подробный, упрощенный и быстрый. Для того чтобы рассчитать поперечную силу в сечении нужно уметь пользоваться уравнениями равновесия конструкции. Поэтому перед изучением данной статьи, если вы не знаете этого материала, рекомендую изучить его, перейдя по указанной ссылке выше. Ну что же перейдем непосредственно к обучению!

Эпюра поперечных сил — это график показывающий распределение поперечных сил в сечениях, загруженного элемента, работающего на поперечный изгиб.

Видео:Построение эпюр при изгибе. Часть 1. Консольная балкаСкачать

Построение эпюр при изгибе. Часть 1. Консольная балка

Подробный способ построения эпюры поперечных сил

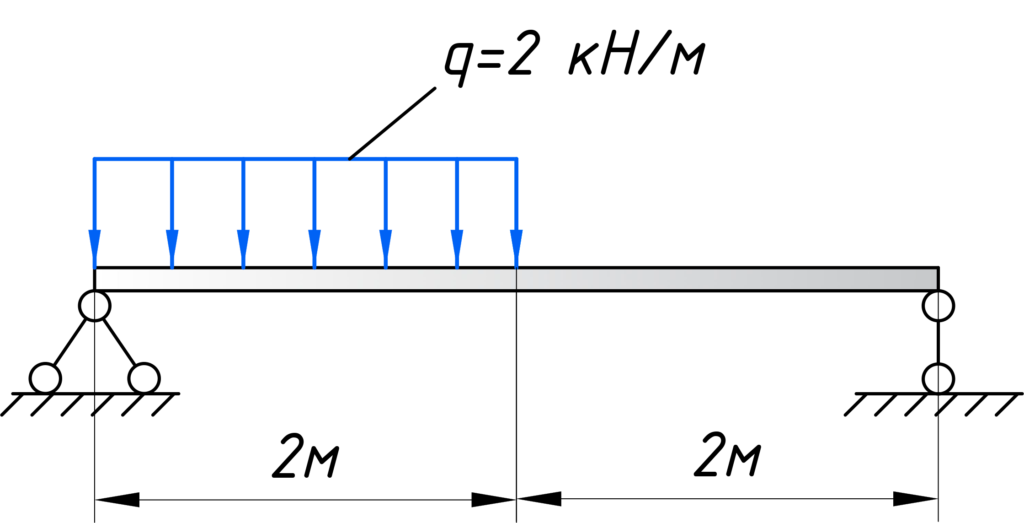
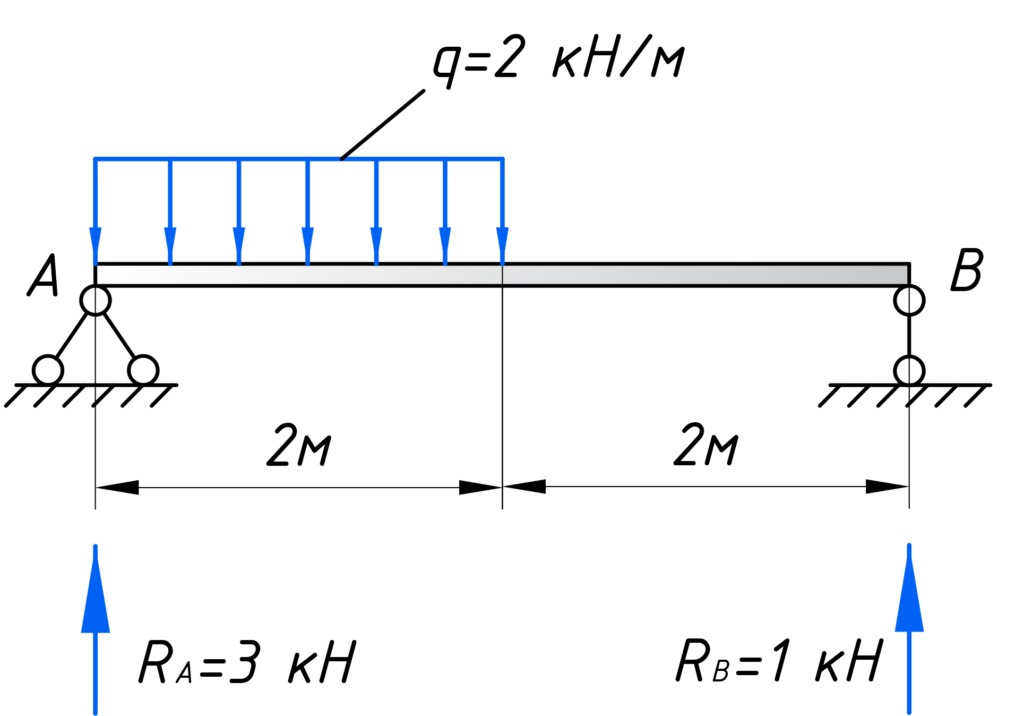
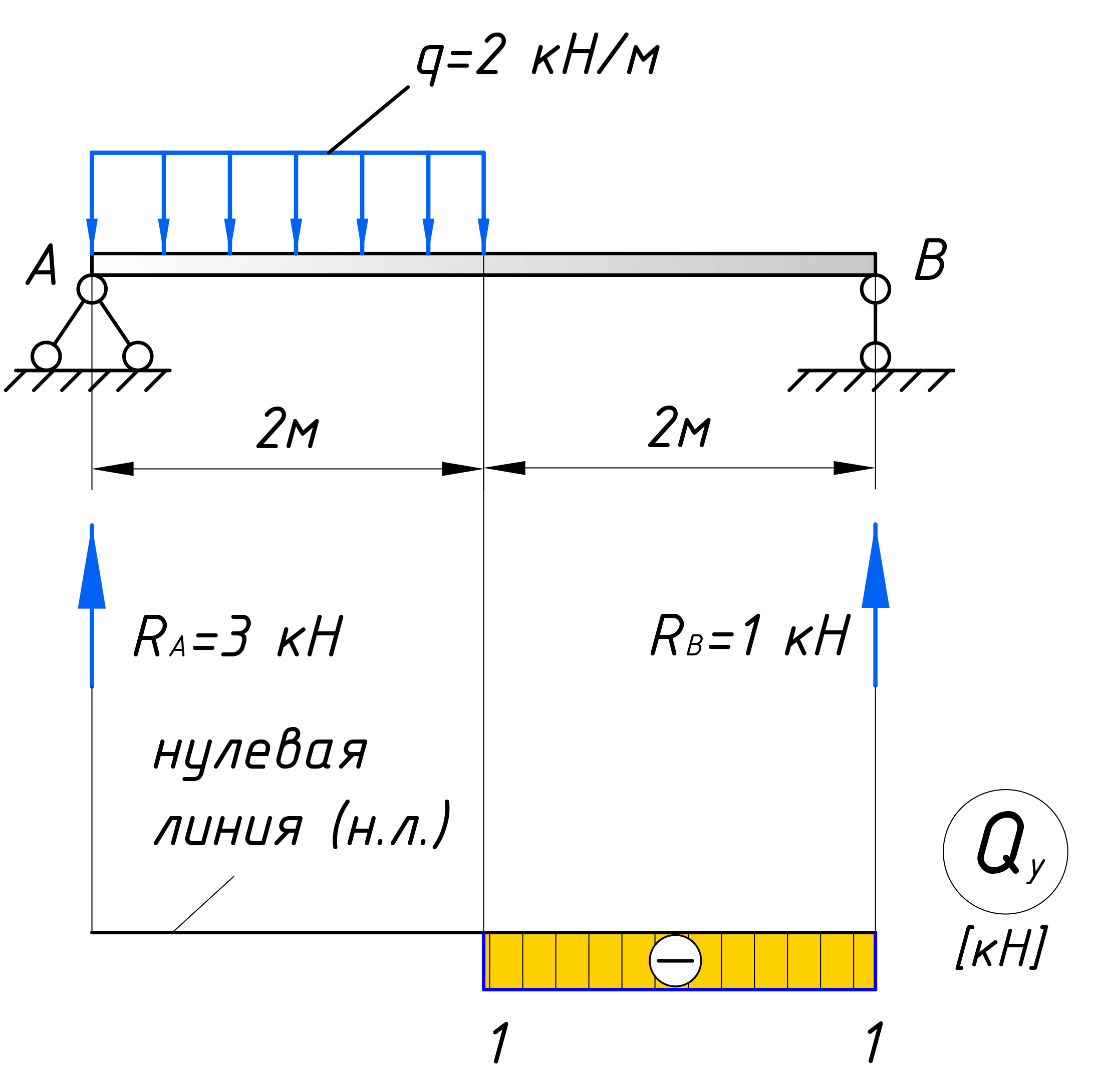
В качестве примера, возьмем балку, частично загрузим ее распределенной нагрузкой q, а часть оставим без нагрузки, чтобы рассмотреть всевозможные случаи:

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Первым делом нужно определить все внешние силы, действующие на конструкцию, то есть помимо распределенной нагрузки на балку будет действовать реакции, возникающие в опорах. Если вы до сих пор не умеете их определять, то обязательно изучите этот материал. В этой статье, я подробно на этом останавливаться не буду. Вот какие значения реакций получаться для рассматриваемого примера:

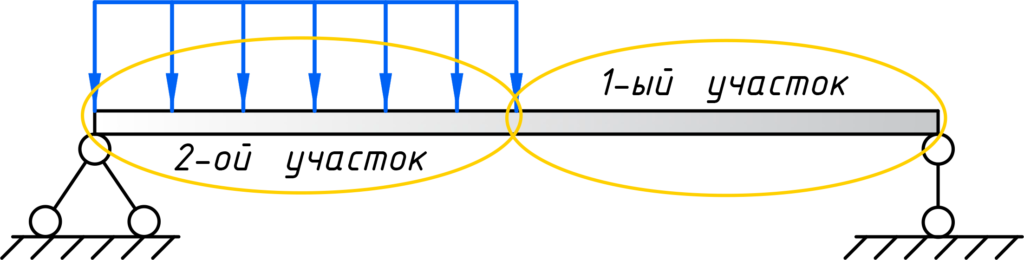
Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Разбиваем балку на участки

После подготовительного этапа можно приступать к расчету поперечных сил. На отдельных участках балки поперечная сила будет меняться по определенному закону. Как раз, наша задача научиться определять эти законы. Зная закон изменения поперечной силы на участке, можно определить ее значения в любом сечении в пределах этого участка. Так как, поперечная сила меняется по линейному закону, для построения эпюры достаточно определить ординаты на границах участков. Границами участков служат места приложения сосредоточенных сил, а также начало и конец распределенной нагрузки, то есть для нашего случая нужно рассмотреть два участка.

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Важно! Для эпюры изгибающих моментов, границей участков также служит место приложения сосредоточенного момента. На эпюру же поперечных сил моменты не оказывают никакого влияния. Однако, так как эпюры поперечных сил и изгибающих моментов строятся, обычно, вместе, то эту границу так же нужно намечать.

Метод сечений

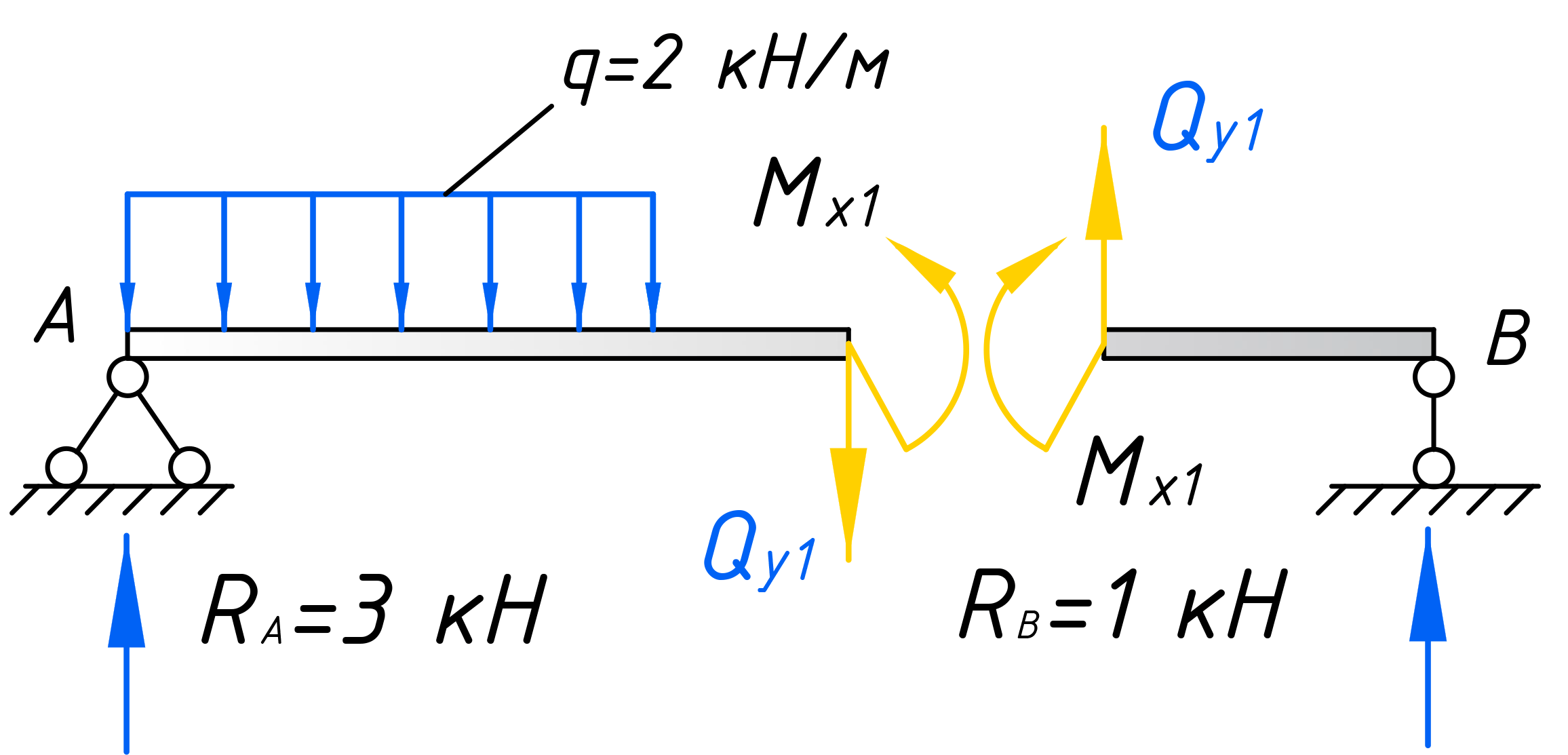
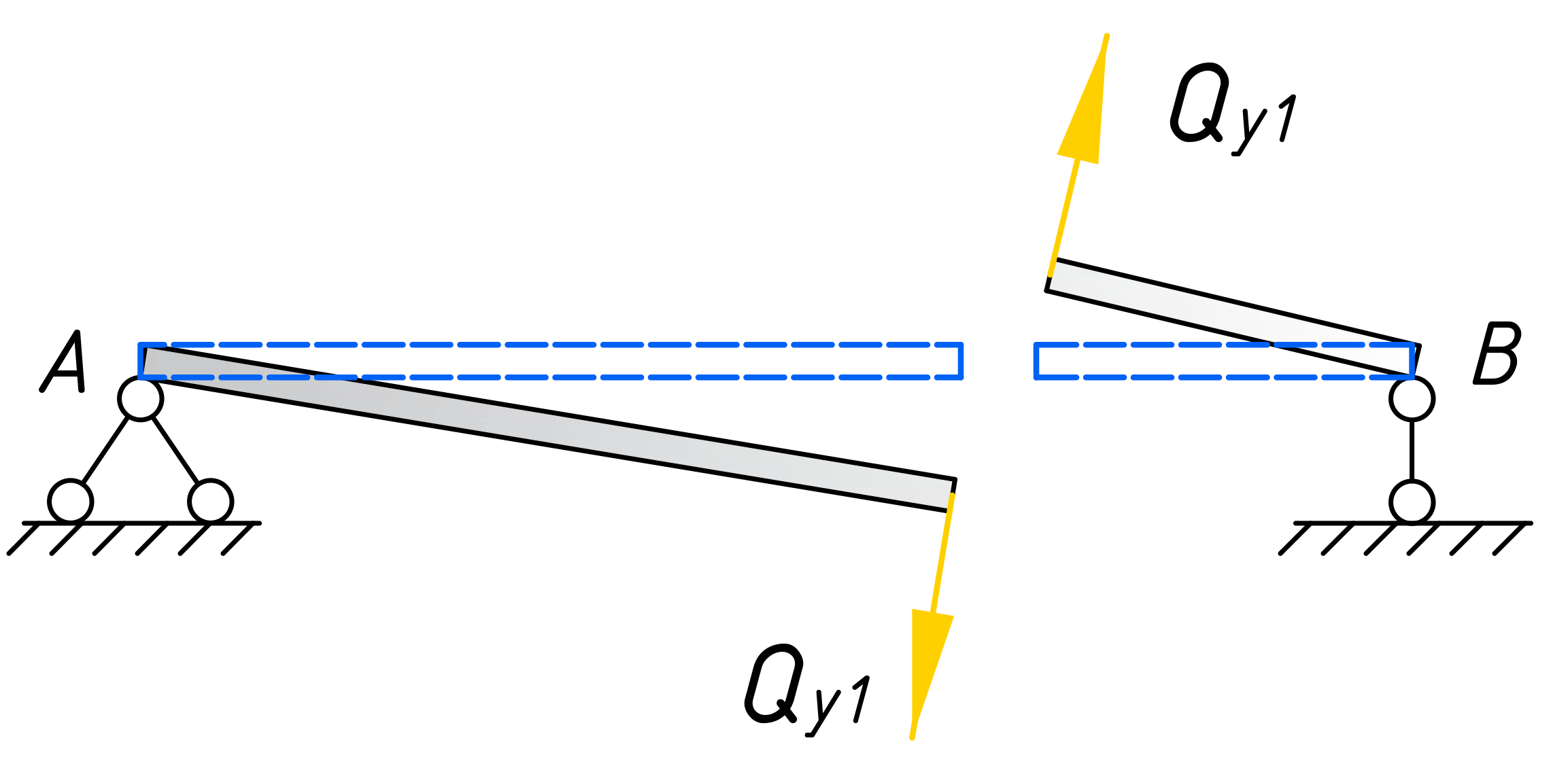
Приступим непосредственно к расчету. Для установления закона изменения поперечной силы, будем использовать метод сечений. Мысленно рассекаем балку на две части, в пределах 1-го участка, на расстоянии x1 от правого торца балки.

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Каждую часть балки уравновешиваем путем приложения сосредоточенной силы Qy1 и момента Mx1. Эти силовые факторы, заменяют действие частей балки друг на друга. Для определения этих величин, достаточно рассмотреть равновесие одной из рассеченных частей.

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Правила знаков для поперечной силы

Очень важно на данном этапе выбрать правильное направление поперечной силы. Она должна иметь такое направление, при котором часть балки, при неподвижном (закрепленном) противоположном от рассечения месте, стремилась повернутся ПО часовой стрелке.

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Также многие авторы рекомендуют просто запомнить такое правило:

  • Для правой отсеченной части, направлять поперечную силу вверх;
  • Для левой отсеченной части, направлять поперечную силу вниз.

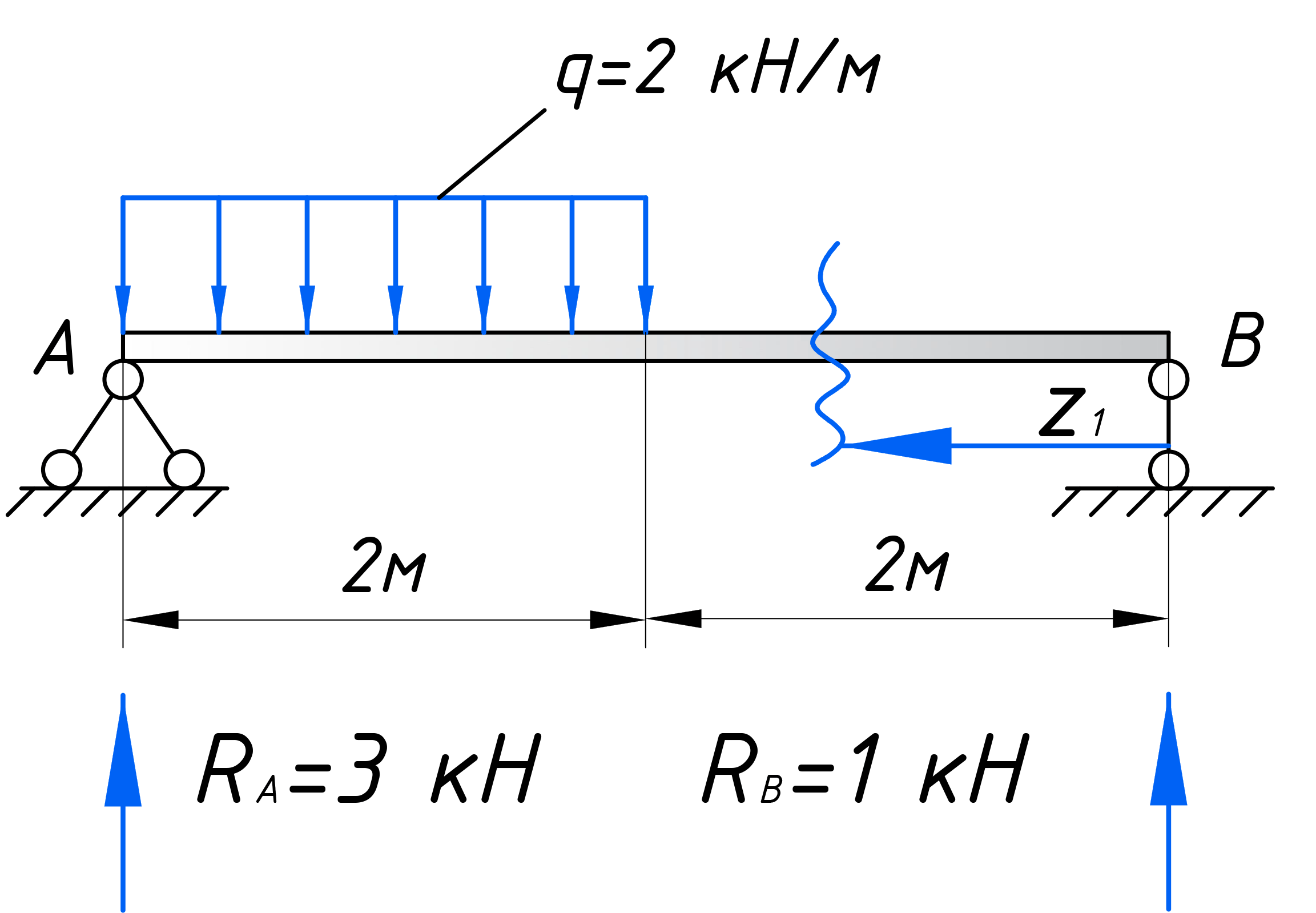
Вводим систему координат для первого участка

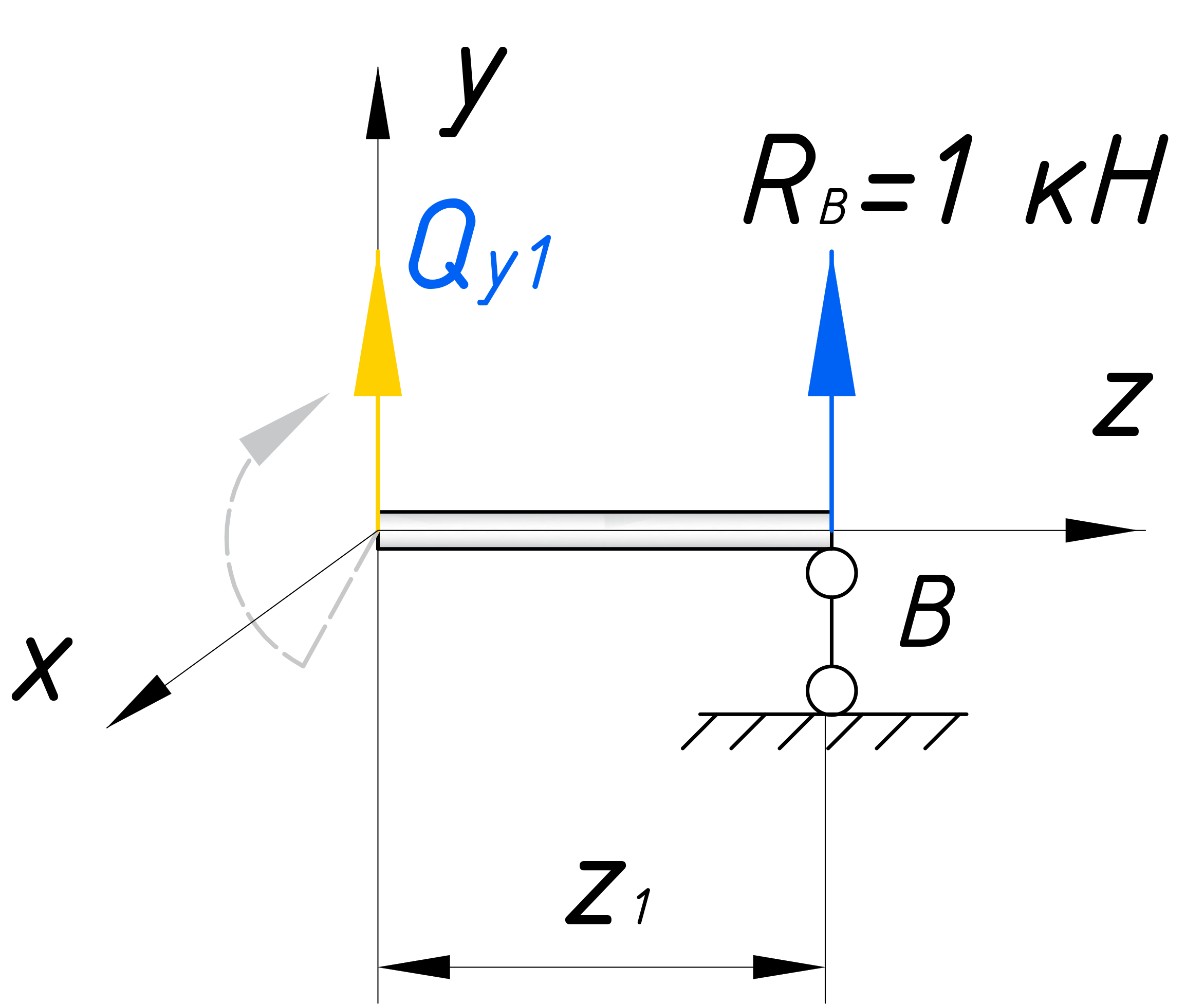
Для удобства выберем правую часть, так как здесь меньше нагрузки, которую нужно учитывать в расчете. Также, мы можем не учитывать момент Mx1, так как в этом уроке, нас интересует только поперечная сила. В рассматриваемом сечении вводим локальную систему координат:

  • Ось z будет иметь горизонтальное направление;
  • Ось y будет направлена вертикально;
  • Ось x будет направлена перпендикулярно плоскости чертежа (на нас).

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Записываем уравнение равновесия для первого участка и строим эпюру

Для нахождения поперечной силы на первом участке достаточно записать одно уравнение равновесия – сумму проекций все сил на вертикальную ось y. Эта сумма должна быть равна нулю:

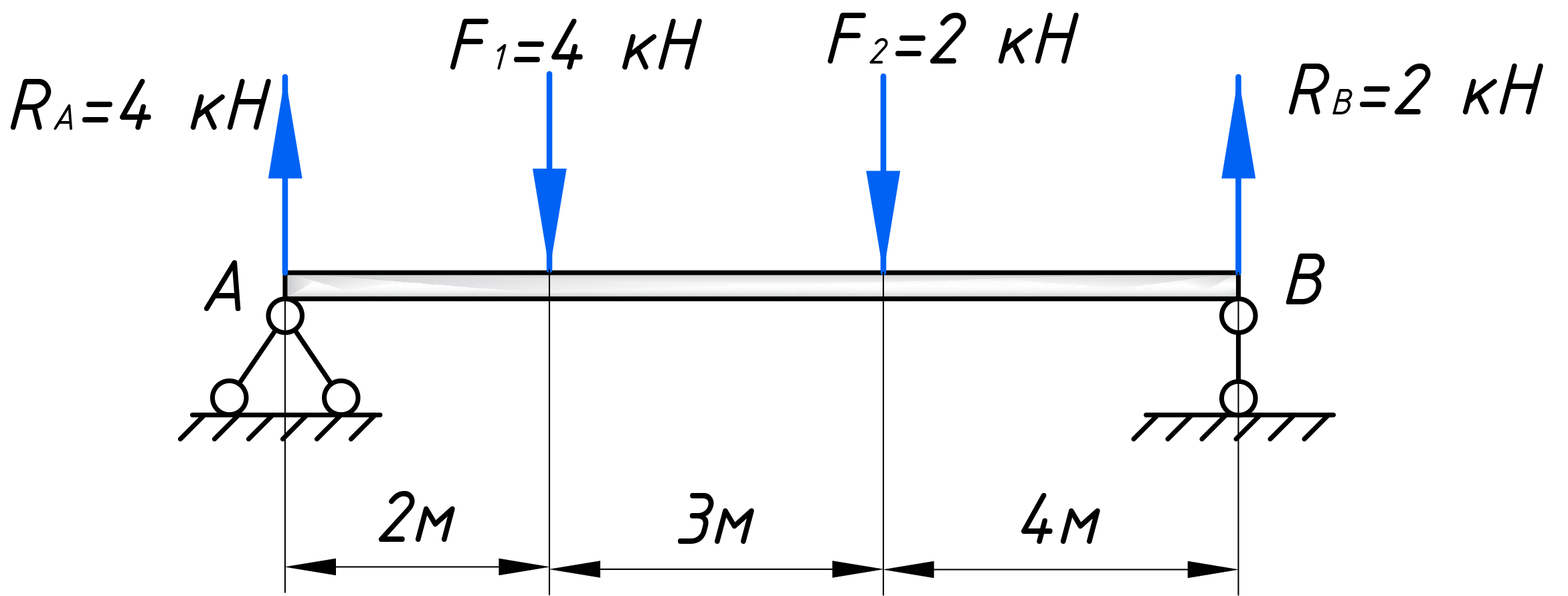
Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Из полученного уравнения, следует:

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Таким образом, поперечная сила в пределах первого участка равна 1 кН. Откладываем это значение на графике:

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Положительное значение поперечной силы откладывается выше нулевой линии, отрицательное ниже (как в нашем случае). Эпюры штрихуются перпендикулярно нулевой линии, на каждом участке проставляются знаки, на границах участков указываются численные значения.

Расчет второго участка

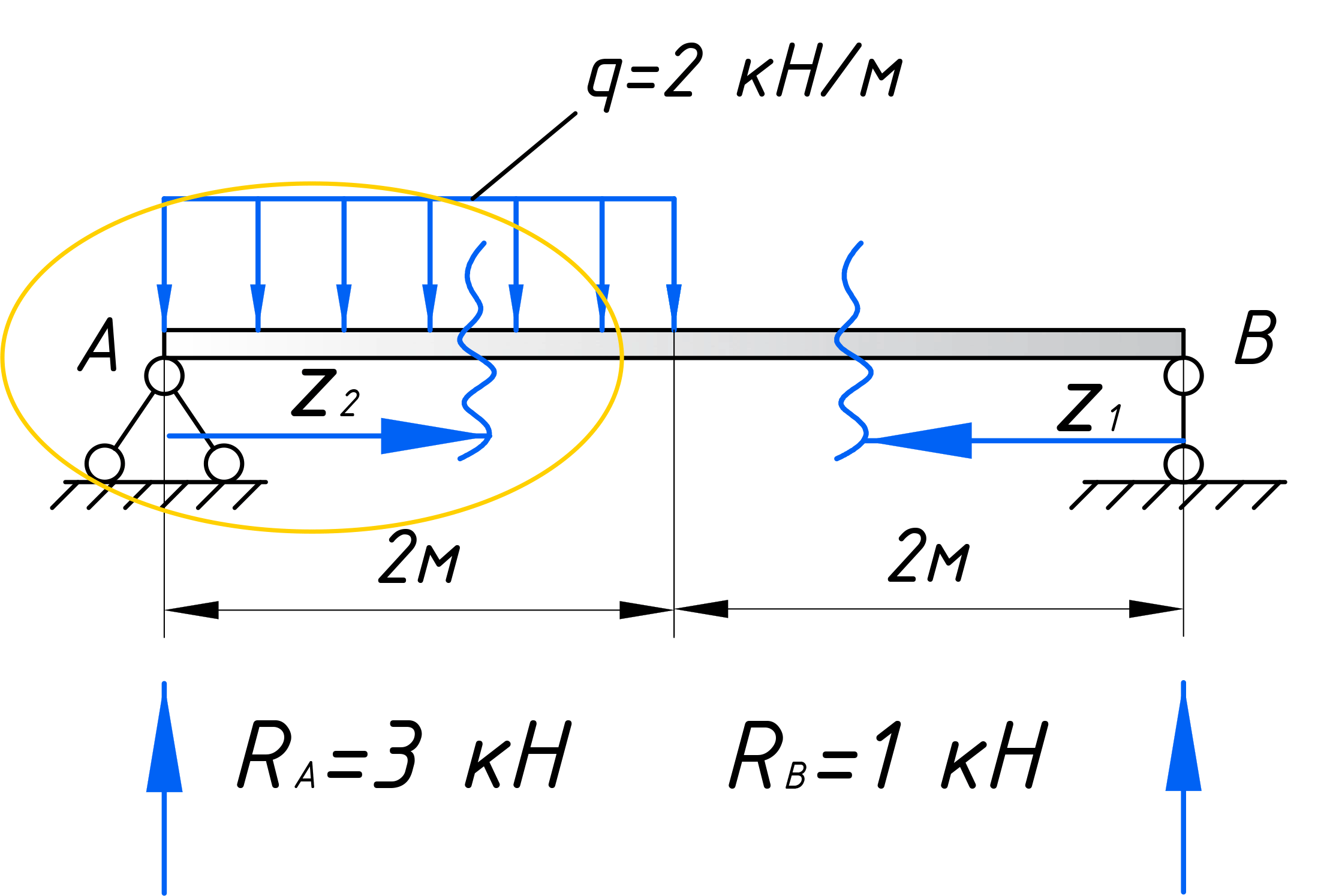
Проделываем те же действия, что выполняли для первого участка. Рассекаем балку в пределах рассматриваемого участка на расстоянии z2 от левого торца балки:

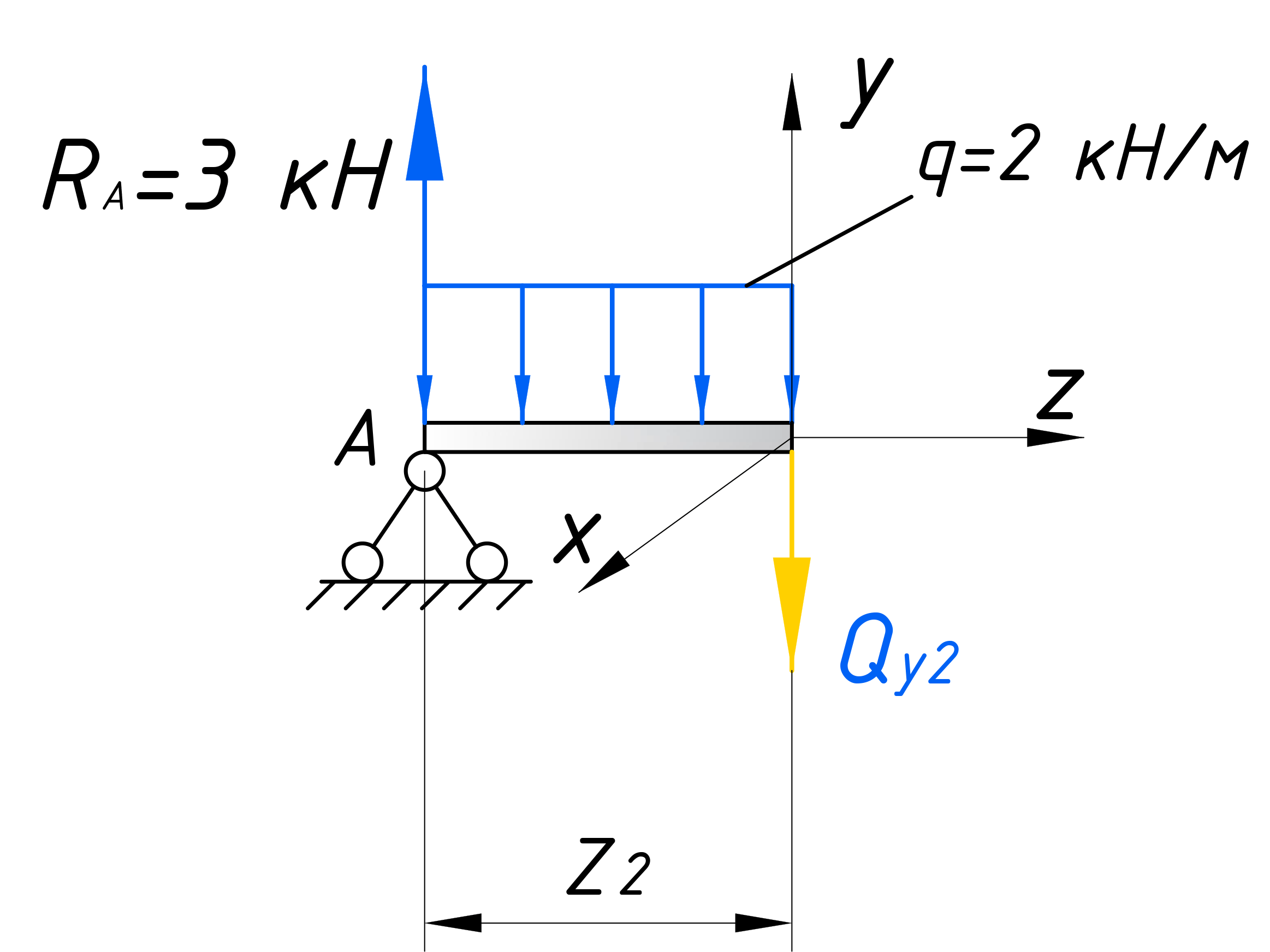
Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Зарисовываем отдельно расчетный элемент, отбросив правую часть и заменив ее действие Qy2 и Mx2. Вводим локальную систему координат:

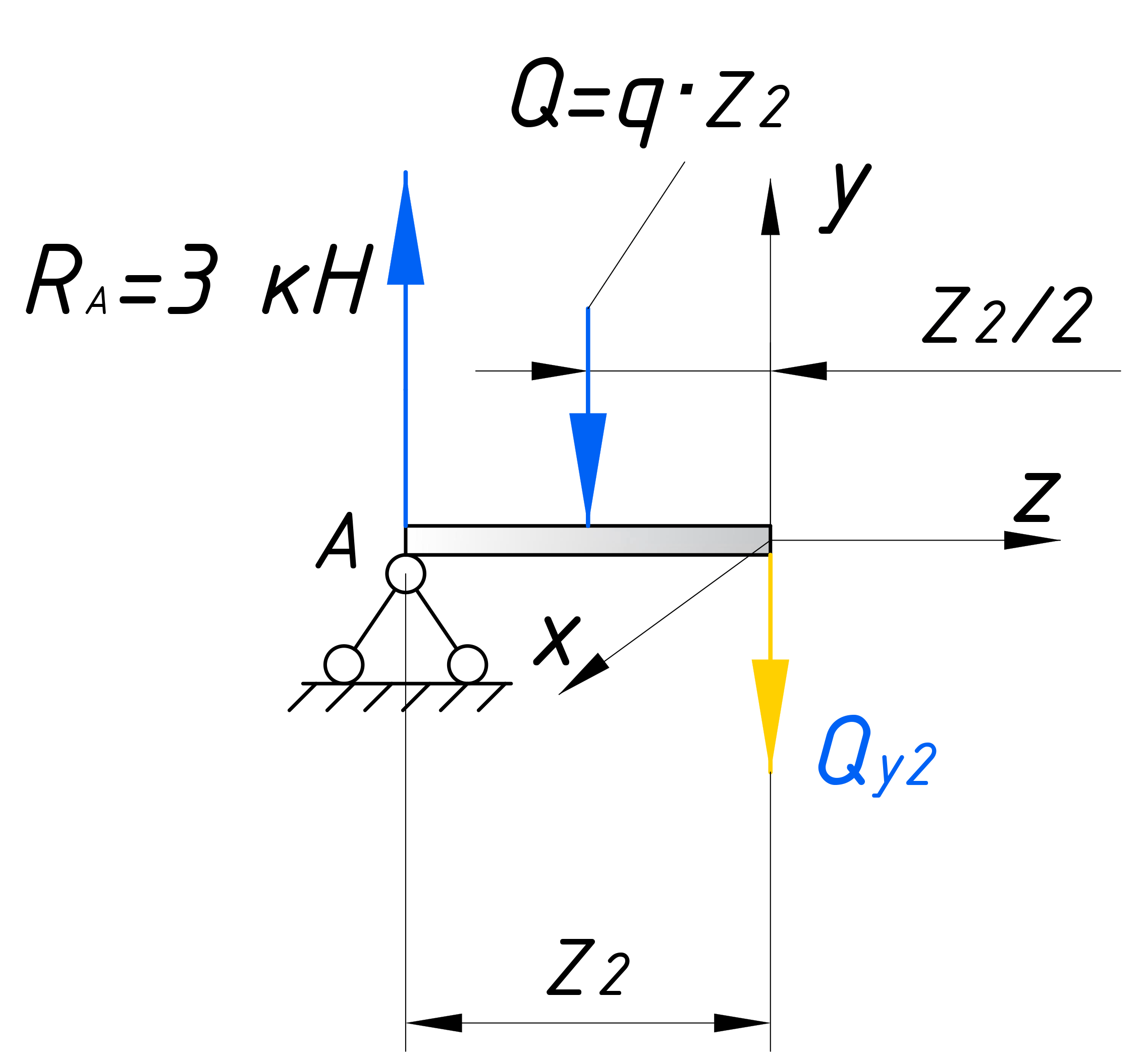
Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Для того чтобы рассчитать такой участок, с распределенной нагрузкой, воспользуемся хитростью, которой часто пользуются при решении задач по теоретической механике. Свернем эту нагрузку до сосредоточенной силы. Для этого умножим интенсивность q на длину действия нагрузки – z2.

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Записываем уравнение равновесия для второго участка:

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Выражаем поперечную силу:

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Это закон, по которому меняется поперечная сила на втором участке. Чтобы получить значения для построения эпюры, нужно в это уравнение вместо z2 подставить координаты характерных сечений. Как и говорилось ранее, поперечная сила меняется по линейному закону (исключениями могут быть только схемы с трапециевидной нагрузкой), поэтому для построения эпюры достаточно вычислить значения на границах участка. В сечении A (при z2=0) поперечная сила будет равна:

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

В середине пролета, при z2=2м получим:

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

По полученным значениям, строим эпюру поперечных сил на втором участке:

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Вот собственно и все! Эпюра поперечных сил построена. Согласитесь, длинное руководство получилось?! Так вот, далее я расскажу, как построить эту эпюру намного быстрее, а в конце покажу как это делается за несколько секунд.Сделайте небольшой перерыв на чай, и возвращайтесь к чтению!

Видео:Расчет значений Q и M для построения эпюр поперечных сил и изгибающих моментов балки на двух опорахСкачать

Расчет значений Q и M для построения эпюр поперечных сил и изгибающих моментов балки на двух опорах

Упрощенный способ построения эпюры

Итак, продолжим изучать технологии построения эпюры поперечных сил. В этом методе будем учиться рассчитывать эту эпюру без вынесения отдельных участков балки и без записи уравнений равновесия. Будем выводить сразу следствия из этих уравнений. Также как, в первом случае, балку нужно разбить на 2 участка.

Первый участок

Запишем закон изменения поперечной силы на первом участке. Для этого отметим сечение С, отстающее от правого торца балки на величину z1. Поперечная сила в этом сечении будет равна сумме проекций всех сил на вертикальную ось, находящихся справа (или слева) от сечения. Мы ведем расчет этого участка справа-налево, так как в данном случае справа нагрузки меньше.

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Для того чтобы правильно записать уравнение поперечных сил для любого участка, нужно придерживаться следующих правил:

  • Если нагрузка относительно рассматриваемого сечения стремится повернуть ПО часовой стрелки, то в уравнении она учитывается со знаком «+»;
  • Если нагрузка относительно рассматриваемого сечения стремится повернуть ПРОТИВ часовой стрелки, то в уравнении она учитывается со знаком «-».

Продемонстрирую вышеописанные правила на нашем примере. Относительно сечения С, сила R B , находящаяся справа от сечения, стремится повернуть против часовой стрелки, поэтому в уравнение она пойдет со знаком «-»:

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Как видно из уравнения, поперечная сила, на первом участке, не зависит от координаты z1, поэтому во всех сечениях она одинаковая.

Кстати, помните я писал, что нагрузку можно учитывать, как справа, так и слева? Так вот, давайте запишем уравнение, просуммировав нагрузку, находящуюся слева от сечения С и посмотрим результат.

Реакция RA, относительно сечения С, стремится повернуть ПО часовой стрелке, в уравнение пойдет с плюсом:

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Нагрузку q, сворачиваем до сосредоточенной силы, как в подробном способе. Она стремится повернуться ПРОТИВ часовой стрелке, в уравнение пойдет со знаком «минус»:

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Подставляя численные значения нагрузки, получим следующий результат:

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Теперь перейдем ко второму участку.

Второй участок

Здесь ситуация похожая, подробно комментировать уже не буду, приведу схему и расчет:

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

По выполненным расчетам двух участков, можно построить уже знакомую эпюру:

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Как видите, эпюра поперечных рассчитывается достаточно просто. В последнем разделе я расскажу, как можно построить ее и вовсе устно.

Видео:Построение эпюр поперечных сил и изгибающих моментов.Скачать

Построение эпюр поперечных сил и изгибающих моментов.

Быстрый способ построения эпюры

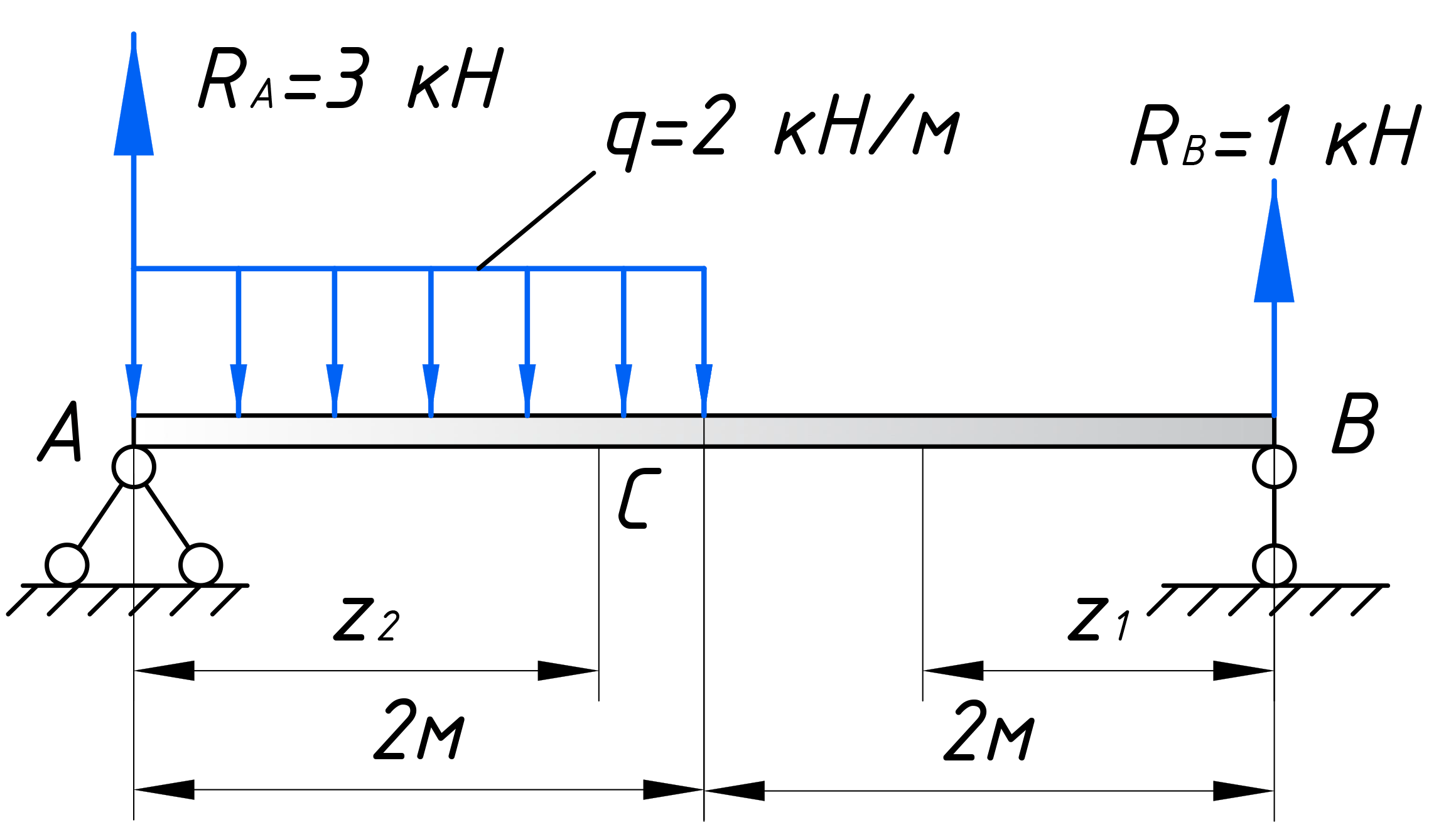
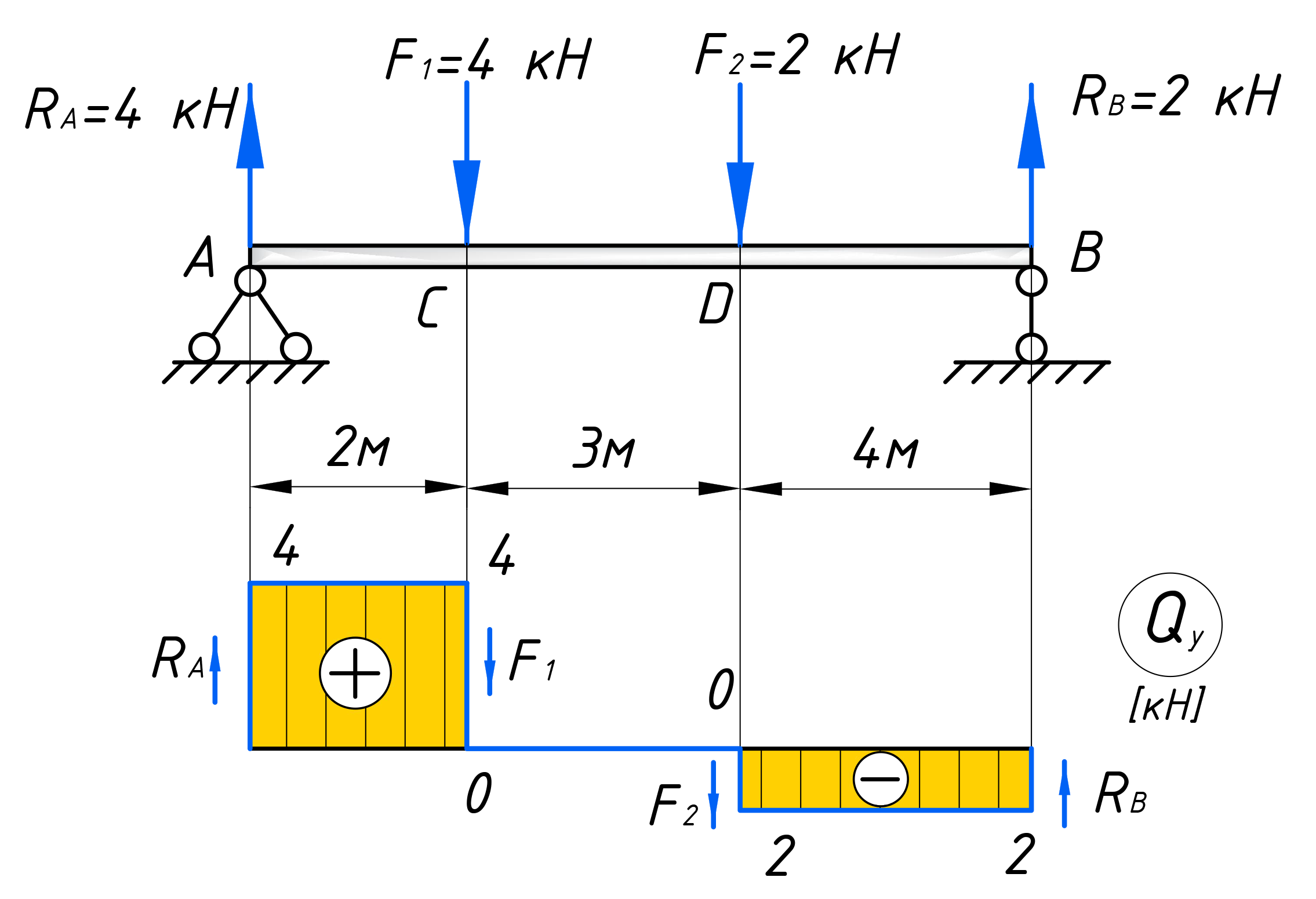
Как вы уже, наверное, заметили, эпюра поперечных сил имеет скачки в тех местах, где прикладываются сосредоточенные усилия, а в местах где приложена распределенная нагрузка, эпюра постоянно меняется по линейному закону. Эти свойства эпюры можно использовать при построении. Давайте рассмотрим такую балку:

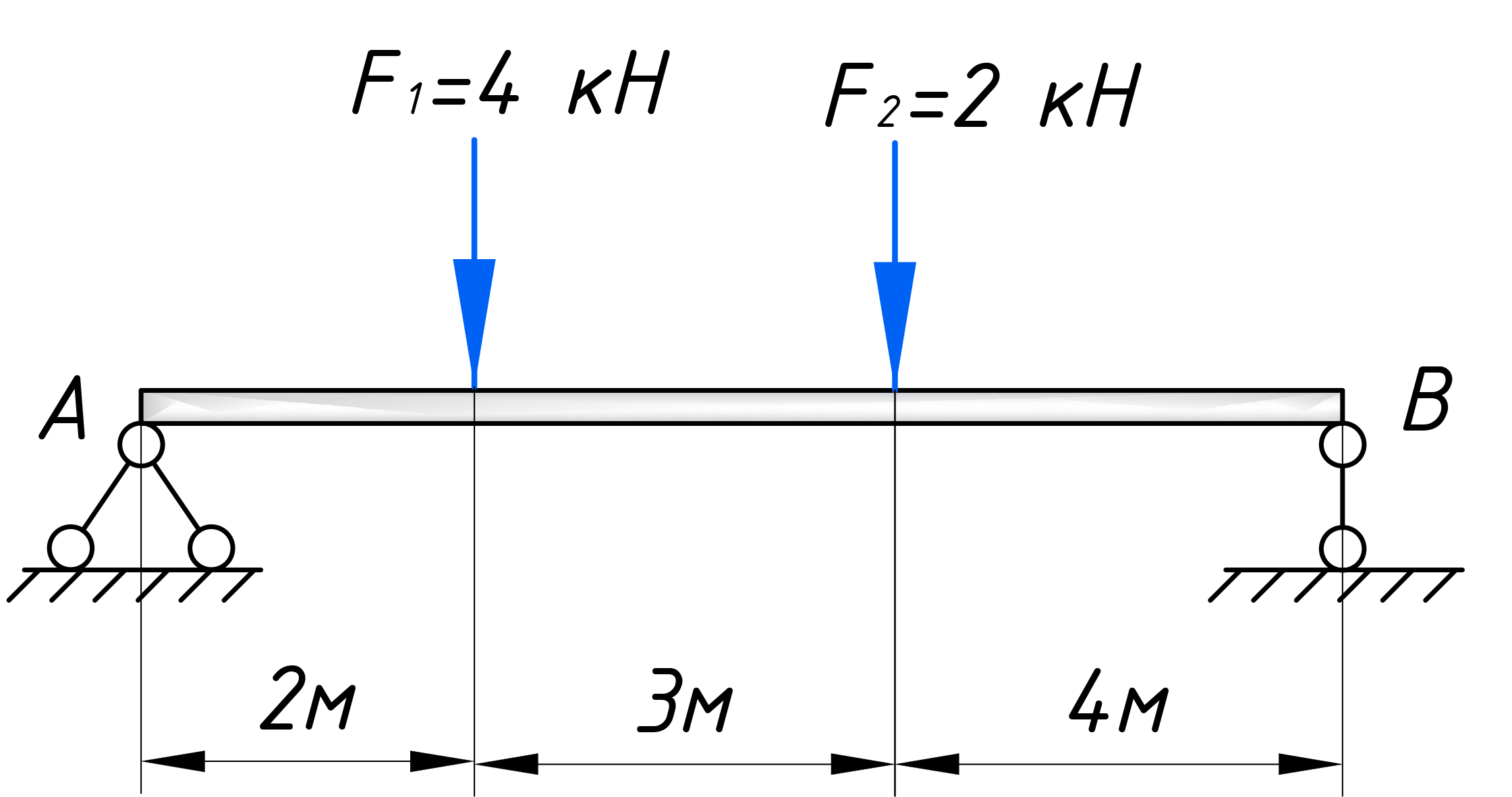
Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Определим для нее опорные реакции:

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Расчет быстрым способом рекомендую производить слева-направо . В этом случае для скачков эпюры будут следующие правила знаков:

  • Если приложенная сила направлена вверх , то и скачек на эпюре будет вверх, на величину силы;
  • Если приложенная сила направлена вниз , то и скачек на эпюре будет вниз, на величину силы.

С учетом данных правил, получим вот такую эпюру поперечных сил:

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Прокомментирую: в точке А, сила направлена вверх, эпюра поднимается на 4 кН, в точке С, опускается до нуля, т.к. приложенная сила направлена вниз и так далее. С сосредоточенным усилиями думаю все просто и понятно.

Уравнения поперечных сил и изгибающих моментов для каждого участка балки

Там, где есть, распределенная нагрузка, эпюра меняется не скачкообразно, а постепенно. И чтобы узнать насколько эпюра измениться от действия распределенной нагрузки от ее начала и до конца, нужно умножить интенсивность q на длину ее действия:

Вот собственно и все, что хотелось рассказать об эпюрах поперечных сил! Вы можете задавать любые вопросы по материалам статьи в комментариях ниже. Также рекомендую подписаться на наши соц. сети, чтобы не пропустить новые и интересные материалы.

После освоения данного урока, можете смело приступать к изучению техник построения эпюр изгибающих моментов. Данная статья является продолжением серии статей о том, как строятся эпюры для балок, работающих на поперечный изгиб.

📹 Видео

Построение эпюр поперечных сил Qy и изгибающих моментов Mx двухопорной балкиСкачать

Построение эпюр поперечных сил Qy и изгибающих моментов Mx двухопорной балки

ЭПЮРЫ. МЕТОД ТОЧЕК. СОПРОМАТ ДЛЯ СТРОИТЕЛЬНЫХ СПЕЦИАЛЬНОСТЕЙ. Балка.Скачать

ЭПЮРЫ. МЕТОД ТОЧЕК. СОПРОМАТ ДЛЯ СТРОИТЕЛЬНЫХ СПЕЦИАЛЬНОСТЕЙ. Балка.

Построение эпюр в консольной балкеСкачать

Построение эпюр в консольной балке

Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Определение опорных реакций балки. Сопромат для чайников ;)

#сопромат #балка - отличие эпюры Q от M #построениеэпюр #онлайнобучениеСкачать

#сопромат #балка - отличие эпюры Q от M #построениеэпюр #онлайнобучение

Сопротивление материалов. Лекция: универсальное уравнение изогнутой оси балкиСкачать

Сопротивление материалов. Лекция: универсальное уравнение изогнутой оси балки

Сопромат Плоский изгиб (построение эпюр и подбор сечений) Задача №3.22Скачать

Сопромат Плоский изгиб (построение эпюр и подбор сечений) Задача №3.22

2. Построение эпюр в балке ( практический курс по сопромату )Скачать

2. Построение эпюр в балке ( практический курс по сопромату )

Уравнение трех моментов. Расчет много пролетной не разрезной балкиСкачать

Уравнение трех моментов. Расчет много пролетной не разрезной балки

30. Статически неопределимая балка ( уравнение трех моментов ) ( практический курс по сопромату )Скачать

30. Статически неопределимая балка ( уравнение трех моментов ) ( практический курс по сопромату )

С.М. задача №6.5 расчёт неразрезной балки с помощью уравнения трёх моментовСкачать

С.М. задача №6.5 расчёт неразрезной балки с помощью уравнения трёх моментов
Поделиться или сохранить к себе: