Предлагаю вам воспользоваться онлайн калькулятором для вычисления угла между плоскостями.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление угла между плоскостями и закрепить пройденный материал.
- Найти угол между плоскостями
- Ввод данных в калькулятор для вычисления угла между плоскостями
- Дополнительные возможности калькулятора вычисления угла между плоскостями
- Теория. Угол между плоскостями
- Угол между плоскостями. Онлайн калькулятор
- Предупреждение
- Угол между плоскостями − теория
- Углы между плоскостями. Как определить угол между плоскостями
- Прямая в пространстве
- Уравнение плоскости
- Расположение плоскостей и формула угла между ними
- Примеры решения задач на определение угла пересечения плоскостей
- Плоскость и прямая
- Прямая и плоскость, значение угла между ними
- Задача: плоскость пересекает прямую
- Задача: параллельная плоскости прямая
- Где важно знать углы между рассмотренными геометрическими объектами?
- Пирамида и ее углы
- 📸 Видео
Видео:21. Угол между прямой и плоскостьюСкачать

Найти угол между плоскостями
Уравнение 1-ой плоскости:
Уравнение 2-ой плоскости:
Ввод данных в калькулятор для вычисления угла между плоскостями
В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора вычисления угла между плоскостями
- Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.
Теория. Угол между плоскостями
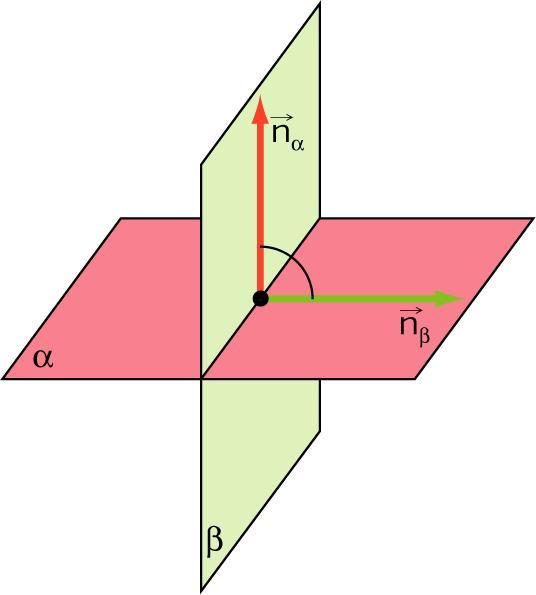
Двугранный угол между плоскостями равен углу образованному их нормальными векторами.
Если заданы уравнения плоскостей A1 x + B1 y + C1 z + D1 = 0 и A2 x + B2 y + C2 z + D2 = 0, то угол между плоскостями можно найти, используя следующую формулу
| cos α = | |A1·A2 + B1·B2 + C1·C2| |
| √ A1 2 + B1 2 + C1 2 √ A2 2 + B2 2 + C2 2 |
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Найти угол между плоскостямиСкачать
Угол между плоскостями. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти угол между плоскостями. Дается подробное решение с пояснениями. Для вычисления угла между плоскостями, введите элементы уравнения плоскостей в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Угол между плоскостями − теория
Пусть заданы две плоскости α и β общими уравнениями
| A1x+B1y+C1z+D1=0, | (1) |
| A2x+B2y+C2z+D2=0 | (2) |
Из определения скалярного произведения, имеем
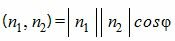 . . | (3) |
Тогда из (3) можно найти косинус угла между нормальными векторами n1 и n2:
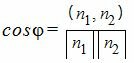 . . | (4) |
Учитывая, что (n1, n2)=A1A2+B1B2+C1C2 и длины векторов |n1|= 
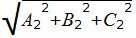
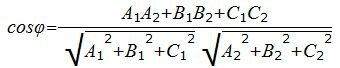 . . | (5) |
Таким образом косинус угла между нормальными векторами и, следовательно, косинус угла между плоскостями α и β определяется формулой (5). Далее можно найти угол φ с помощью функции arccos.
Отметим, что пересекающиеся плоскости образую два угла. Другой угол можно найти так: φ‘=180−φ.
Видео:Метод координат для ЕГЭ с нуля за 30 минут.Скачать

Углы между плоскостями. Как определить угол между плоскостями
При решении геометрических задач в пространстве часто встречаются такие, где необходимо рассчитать углы между разными пространственными объектами. В данной статье рассмотрим вопрос нахождения углов между плоскостями и между ними и прямой.
Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Прямая в пространстве
Известно, что совершенно любая прямая на плоскости может быть определена следующим равенством:
Здесь a и b — некоторые числа. Если представить тем же самым выражением прямую в пространстве, то получится уже плоскость, параллельная оси z. Для математического определения пространственной прямой применяют иной способ решения, чем в двумерном случае. Он заключается в использовании понятия «направляющий вектор».

Направляющий вектор прямой показывает ее ориентацию в пространстве. Этот параметр принадлежит прямой. Поскольку существует бесконечное множество параллельных в пространстве векторов, то для однозначного определения рассматриваемого геометрического объекта необходимо также знать координаты точки, принадлежащей ему.
Предположим, что имеется точка P(x0; y0; z0) и направляющий вектор v¯(a; b; c), тогда уравнение прямой может быть задано следующим образом:
(x; y; z ) = P + α * v¯ или
(x; y; z) = (x0; y0; z0) + α * (a; b; c)
Это выражение называется параметрическим векторным уравнением прямой. Коэффициент α является параметром, который может принимать абсолютно любые действительные значения. Координаты прямой можно представить явно, раскрывая это равенство:

Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Уравнение плоскости
Известно несколько форм записи уравнения для плоскости в пространстве. Здесь же рассмотрим одну из них, которая чаще всего используется при расчете углов между двумя плоскостями или между одной из них и прямой.
Если известен некоторый вектор n¯(A; B; C), который перпендикулярен искомой плоскости, а также указана точка P(x0; y0; z0), которая принадлежит ей же, то общее уравнение для последней имеет вид:
A * x + B * y + C * z + D = 0, где D = -1 * (A * x0 + B * y0 + C * z0)
Мы опустили вывод этого выражения, который является достаточно простым. Здесь лишь заметим, что, зная коэффициенты при переменных в уравнении плоскости, можно с легкостью найти все вектора, которые ей перпендикулярны. Последние называются нормалями и используются при расчетах углов между наклонной и плоскостью и между произвольными аналогами.
Видео:Урок 8. Угол между плоскостями. Стереометрия с нуля.Скачать
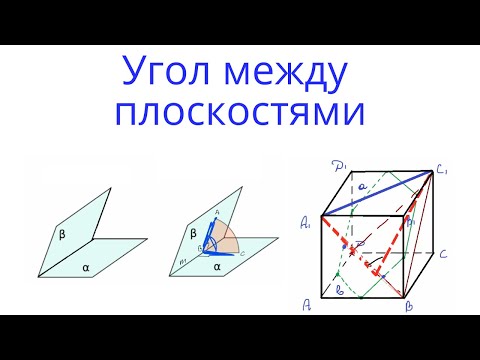
Расположение плоскостей и формула угла между ними
Допустим, имеются две плоскости. Какие существуют варианты их взаимного расположения в пространстве. Поскольку плоскость имеет два бесконечных размера и один нулевой, то возможны лишь два варианта их взаимной ориентации:
- они будут параллельными друг другу;
- они могут пересекаться.

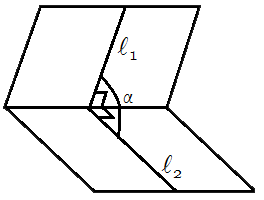
Углом между плоскостями называется показатель между их направляющими векторами, то есть между их нормалями n1¯ и n2¯.
Очевидно, что если являются параллельными плоскости, то угол пересечения равен нулю между ними. Если же они пересекаются, то он отличен от нуля, но всегда является острым. Частным случаем пересечения будет угол 90o, когда плоскости взаимно перпендикулярны друг другу.
Угол α между n1¯ и n2¯ легко определяется из произведения скалярного этих векторов. То есть имеет место формула:
α = arccos((n1¯ * n2¯)/(|n1¯| * |n2¯|))
Предположим, что координаты этих векторов следующие: n1¯(a1; b1; c1), n2¯(a2; b2; c2). Тогда, используя формулы для расчета скалярного произведения и модулей векторов через их координаты, выражение выше можно переписать в виде:
α = arccos(|a1 * a2 + b1 * b2 + c1 * c2| / (√(a12 + b12 + c12) * √(a22 + b22 + c22)))
Модуль в числителе появился потому, чтобы исключить значения тупых углов.
Видео:Координатный метод, уравнение плоскости, угол между плоскостями | Профильная математика ЕГЭ 2023Скачать

Примеры решения задач на определение угла пересечения плоскостей
Зная, как найти между плоскостями угол, решим следующую задачу. Даны две плоскости, уравнения которых имеют вид:
3 * x + 4 * y — z + 3 = 0;
-x — 2 * y + 5 * z +1 = 0
Чему между плоскостями равен угол?
Чтобы ответить на вопрос задачи, вспомним, что коэффициенты, стоящие при переменных в уравнении плоскости общем, являются координатами вектора направляющего. Для указанных плоскостей имеем следующие координаты их нормалей:
Теперь найдем произведение скалярное этих векторов и их модули, имеем:
(n1¯ * n2¯) = -3 -8 -5 = -16;
|n1¯| = √(9 + 16 + 1 ) = √26;
|n2¯| = √(1 + 4 + 25) = √30
Теперь можно подставить найденные числа в приведенную в предыдущем пункте формулу. Получаем:
α = arccos(|-16 | / (√26 * √30) ≈ 55,05o
Полученное значение соответствует острому углу пересечения плоскостей, указанных в условии задачи.
Теперь рассмотрим другой пример. Даны две плоскости:
3 * x + 3 * y + 8 = 0
Пересекаются ли они? Выпишем значения координат их направляющих векторов, посчитаем скалярное произведение их и модули:
(n1¯ * n2¯) = 3 + 3 + 0 = 6;
Тогда угол пересечения равен:
α = arccos(|6| / (√2 * √18) =0o.
Этот угол говорит о том, что плоскости не пересекаются, а являются параллельными. Тот факт, что они не совпадают друг с другом проверить просто. Возьмем для этого произвольную точку, принадлежащую первой из них, например, P(0; 3; 2). Подставим ее координаты во второе уравнение, получим:

3 * 0 +3 * 3 + 8 = 17 ≠ 0
То есть точка P принадлежит только первой плоскости.
Таким образом, две плоскости параллельными являются, когда таковыми будут их нормали.
Видео:10 класс, 21 урок, Угол между прямой и плоскостьюСкачать

Плоскость и прямая
В случае рассмотрения взаимного расположения между плоскостью и прямой существует несколько больше вариантов, чем с двумя плоскостями. Связан этот факт с тем, что прямая является одномерным объектом. Прямая и плоскость могут быть:
- взаимно параллельными, в этом случае плоскость не пересекает прямую;
- последняя может принадлежать плоскости, при этом она также будет параллельна ей;
- оба объекта могут пересекаться под некоторым углом.
Рассмотрим сначала последний случай, поскольку он требует введения понятия об угле пересечения.
Видео:Лекция 25. Виды уравнений плоскости в пространстве.Скачать

Прямая и плоскость, значение угла между ними
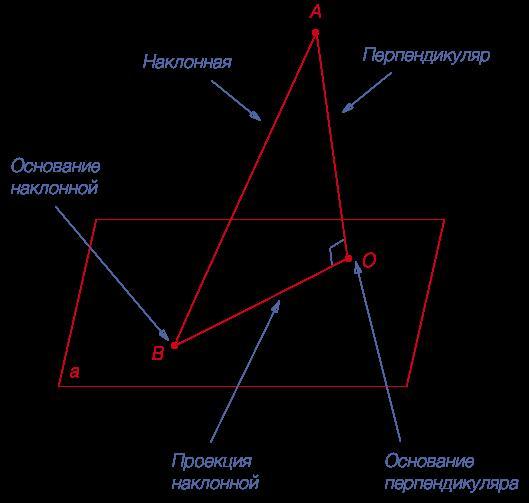
Если плоскость прямая пересекает, то она называется наклонной по отношению к ней. Точку пересечения принято называть основанием наклонной. Чтобы определить между этими геометрическими объектами угол, необходимо опустить из любой точки прямой перпендикуляр на плоскость. Тогда точка пересечения перпендикуляра с плоскостью и место пересечения с ней наклонной образуют прямую. Последняя называется проекцией исходной прямой на рассматриваемую плоскость. Острый угол между прямой и проекцией ее является искомым.
Несколько запутанное определение угла между плоскостью и наклонной прояснит рисунок ниже.
Здесь угол ABO — это угол между AB прямой и a плоскостью.
Чтобы записать формулу для него, рассмотрим пример. Пусть имеется прямая и плоскость, которые описываются уравнениями:
(x ; y ; z ) = (x0; y0; z0) + λ * (a; b; c);
A * x + B * x + C * x + D = 0
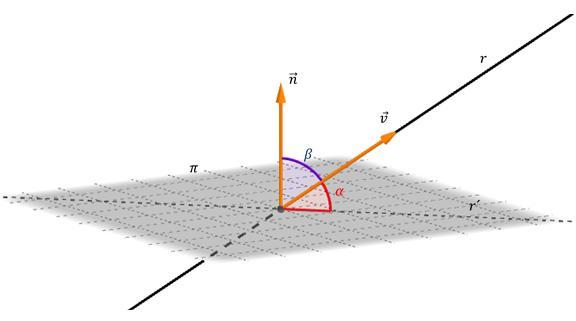
Рассчитать искомый угол для этих объектов можно легко, если найти скалярное произведение между направляющими векторами прямой и плоскости. Полученный острый угол следует вычесть из 90o, тогда он получается между прямой и плоскостью.
Рисунок выше демонстрирует описанный алгоритм нахождения рассматриваемого угла. Здесь β — это угол между нормалью и прямой, а α — между прямой и ее проекцией на плоскость. Видно, что их сумма равна 90o.
Выше была представлена формула, дающая ответ на вопрос, как между плоскостями найти угол. Теперь приведем соответствующее выражение для случая прямой и плоскости:
α = arcsin(|a * A + b * B + c * C| / (√(a 2 + b2 + c 2) * √(A 2 + B 2 + C 2)))
Модуль в формуле позволяет вычислять только острые углы. Функция арксинуса появилась вместо арккосинуса благодаря использованию соответствующей формулы приведения между тригонометрическими функциями (cos(β) = sin(90o-β) = sin(α)).
Видео:Метод координат Урок №2 2 Нахождение уравнения плоскости по трем точкамСкачать

Задача: плоскость пересекает прямую
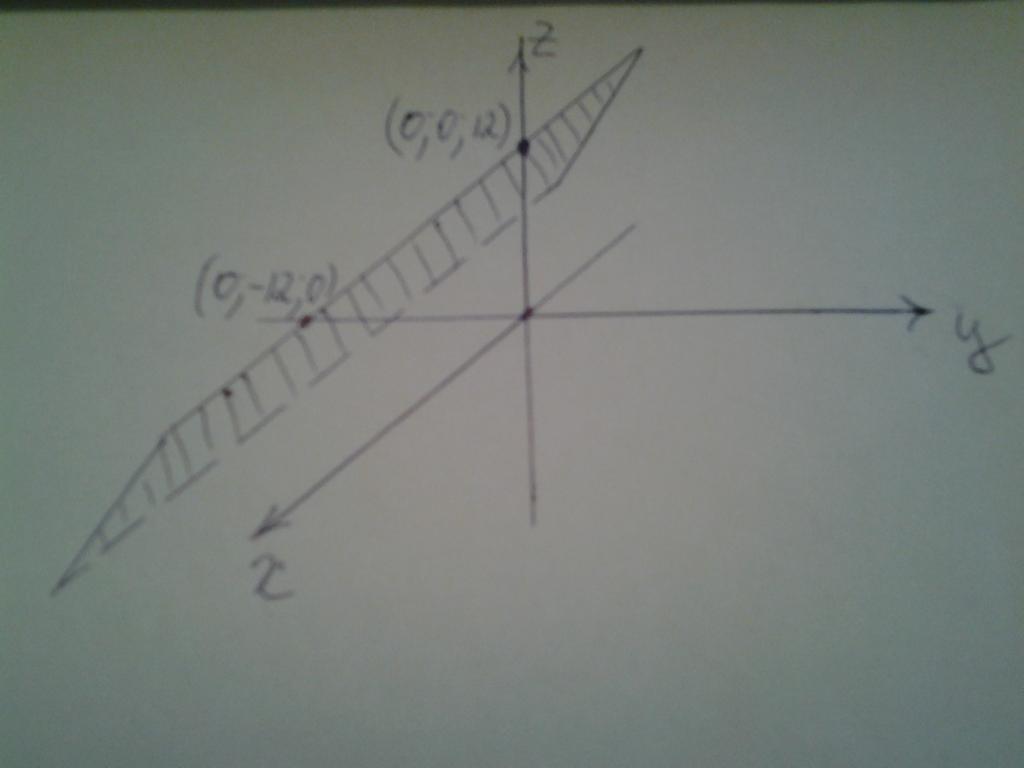
Теперь покажем, как работать с приведенной формулой. Решим задачу: необходимо вычислить угол между осью y и плоскостью, заданной уравнением:
Эта плоскость показана на рисунке.
Видно, что она пересекает оси y и z в точках (0; -12; 0) и (0; 0; 12) соответственно и параллельна оси x.
Направляющий вектор прямой y имеет координаты (0; 1; 0). Вектор, перпендикулярный заданной плоскости, характеризуется координатами (0; 1; -1). Применяем формулу для угла пересечения прямой и плоскости, получаем:
α = arcsin(|1| / (√1 * √2)) = arcsin(1 / √2) = 45o
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Задача: параллельная плоскости прямая
Теперь решим аналогичную предыдущей задачу, вопрос которой поставлен иначе. Известны уравнения плоскости и прямой:
(x; y; z) = (1; 0; 0) + λ * (0; 2; 2)
Необходимо выяснить, являются ли эти геометрические объекты параллельными друг другу.
Имеем два вектора: направляющий прямой равен (0; 2; 2) и направляющий плоскости равен (1; 1; -1). Находим их скалярное произведение:
0 * 1 + 1 * 2 — 1 * 2 = 0
Полученный ноль говорит о том, что угол между этими векторами равен 90o, что доказывает прямой и плоскости параллельность.
Теперь проверим, является эта прямая только параллельной или же еще и лежит в плоскости. Для этого следует выбрать произвольную точку на прямой и проверить, принадлежит ли она плоскости. Например, примем λ = 0, тогда точка P(1; 0; 0) прямой принадлежит. Подставляем в уравнение плоскости P:
Точка P плоскости не принадлежит, а значит, и вся прямая в ней не лежит.
Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Где важно знать углы между рассмотренными геометрическими объектами?
Приведенные выше формулы и примеры решения задач представляют собой не только теоретический интерес. Они часто применяются для определения важных физических величин реальных объемных фигур, например призмы или пирамиды. Важно уметь определить между плоскостями угол при расчете объемов фигур и площадей их поверхностей. При этом, если в случае прямой призмы можно не использовать эти формулы для определения указанных величин, то для любого вида пирамиды их применение оказывается неизбежным.
Ниже рассмотрим пример использования изложенной теории для определения углов пирамиды с квадратным основанием.
Видео:Уравнение плоскости. 11 класс.Скачать

Пирамида и ее углы
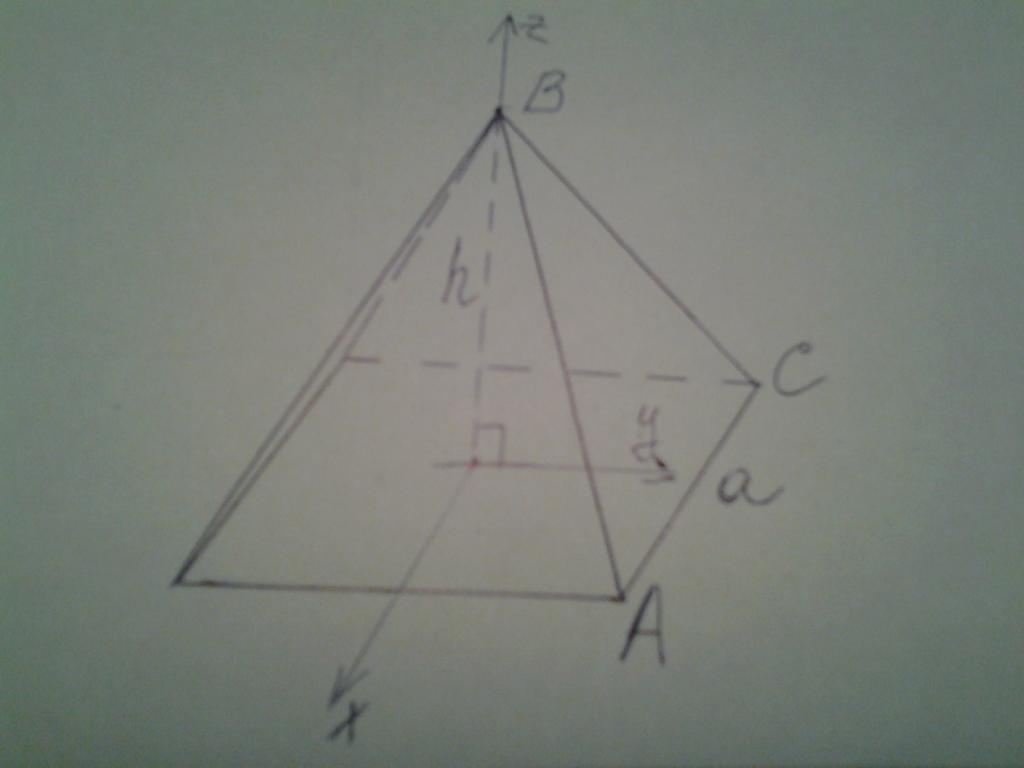
Ниже рисунок демонстрирует пирамиду, в основании которой лежит квадрат со стороной а. Высота фигуры составляет h. Нужно найти два угла:
- между боковой поверхностью и основанием;
- между боковым ребром и основанием.
Чтобы решить поставленную задачу, сначала следует ввести систему координат и определить параметры соответствующих вершин. На рисунке показано, что начало координат совпадает с точкой в центре квадратного основания. В этом случае плоскость основания описывается уравнением:
То есть для любых x и y значение третьей координаты всегда равно нулю. Боковая плоскость ABC пересекает ось z в точке B(0; 0; h), а ось y в точке с координатами (0; a/2; 0). Ось x она не пересекает. Это означает, что уравнение плоскости ABC можно записать в виде:
y / (a / 2) + z / h = 1 или
2 * h * y + a * z — a * h = 0
Вектор AB¯ является боковым ребром. Координаты его начала и конца равны: A(a/2; a/2; 0) и B(0; 0; h). Тогда координаты самого вектора:
Мы нашли все необходимые уравнения и вектора. Теперь остается воспользоваться рассмотренными формулами.
Рассчитаем сначала в пирамиде угол между плоскостями основания и боковой стороны. Соответствующие нормальные вектора равны: n1¯(0; 0; 1) и n2¯(0; 2*h; a). Тогда угол составит:
α = arccos(a / √(4 * h2 + a2 ))
Угол между плоскостью и ребром AB будет равен:
β = arcsin(h / √(a2 / 2 + h2 ))
Остается подставить конкретные значения стороны основания a и высоты h, чтобы получить необходимые углы.
📸 Видео
11 класс, 7 урок, Вычисление углов между прямыми и плоскостямиСкачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Уравнение плоскости. Практика. Урок 5. Геометрия 11 классСкачать

3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

найти уравнения биссектрис углов между прямымиСкачать