Уравнения пьезопроводности при неустановившихся режимах (6 видео)

УРАВНЕНИЕ ПЬЕЗОПРОВОДНОСТИ

ГИДРОДИНАМИЧЕСКИЕ ИССЛЕДОВАНИЯ СКВАЖИН

Курс лекций

Томск 2007

ВВЕДЕНИЕ

ГДИС — система мероприятий, проводимых на скважинах по специальным программам, т.е. замер с помощью глубинных приборов ряда величин (изменения забойных давлений, дебитов, температур во времени и др), последующая обработка замеряемых данных, анализ и интерпретация полученной информации о продуктивных характеристиках — параметрах пластов и скважин.

Цели ГДИС:

Стадия промышленной разведки месторождения

получение возможно полной информации о строении и свойствах пластов, необходимой для подсчета запасов и составления проекта разработки, т.е. выявление общей картины неоднородностей пласта по площади.

Стадии пробной эксплуатации и промышленной разработки месторождения:

· уточнение данных о гидродинамических свойствах разрабатываемого объекта, необходимых для дальнейшего проектирования;

· получение информации о динамике процесса разработки, необходимой для его регулирования;

· определение технологической эффективности мероприятий, направленных на интенсификацию добычи нефти (обработка призабойных зон скважин, гидроразрыв и т.д.).

Методология интерпретации данных ГДИС заключается в определении параметров системы по известным входным и выходным сигналам. При воздействии возмущающим сигналом (постоянный дебит) на систему (скважина и пласт) измеряется реакция системы (изменение забойного давления).

Цель интерпретации ГДИС — определить и охарактеризовать систему по известным входным и выходным сигналам — ОБРАТНАЯ ЗАДАЧА (рис, 1.1.2 Б).

При интерпретации ГДИС исследуются различные теоретические модели системы, которые связывают изменение давления с изменением дебита. Модель и её параметры подбираются таким образом, чтобы по известному входному сигналу (соответствующему «предыстории» работы скважины) получить отклик системы, идентичный реальным испытаниям скважины, тогда параметры модели будут соответствовать параметрам системы — ПРЯМАЯ ЗАДАЧА (рис. 1.1.2 А).

В процессе интерпретации ГДИС можно столкнуться с определенными трудностями, то есть модель может вести себя так же, как реальный пласт, но физические допущения могут быть изначально неверными. Однако реальная опасность ошибки может быть снижена более тщательным проектированием ГДИС. В большинстве случаев проектирование и интерпретация ГДИС зависят от задач, которые при этом необходимо решить.

ТИПЫ ГДИС

Гидродинамические исследования падения давления в добывающей скважине на неустановившемся режиме фильтрации (КПД) — в момент времени t = .0 скважина мгновенно пускается в эксплуатацию (после продолжительного периода простоя) с постоянным дебитом q (рис. 1.2.1).

Определение параметров пласта и скважины при данном методе исследования скважин предполагает:

постоянный дебит q = const;

к моменту времени t = 0 пласт находится в статическом состоянии, т.е. давление по всему пласту постоянно и равно p_j.

Однако на практике очень трудно достичь желаемых условий вследствие ряда причин:

· сложно поддерживать постоянный дебит, даже после того, как приток более или менее стабилизировался;

· скважина не обязательно находится в статическом состоянии, особенно если она была недавно пробурена или эксплуатировалась определенный период перед проведением исследований.

С другой стороны, снятие КПД — хороший метод для определения размеров блока/пласта. Время, необходимое для того, чтобы перераспределение давления достигло границ пласта, достаточно большое, следовательно, эксплуатационные колебания дебита становятся менее существенными. К тому же нет необходимости на долгое время останавливать скважину, что очень важно с экономической точки зрения.

Гидродинамические исследования восстановления давления в добывающей скважинена неустановившемся режиме фильтрации (КВД) — скважина, работавшая определенный период времени t_p с постоянным дебитом q, останавливается и измеряется восстановление давления на забое (рис, 1.2.2).

Определение параметров пласта и скважины приданном методе исследования скважин предполагает:

· постоянный дебит q=const перед закрытием скважины

· скважина должна работать достаточный период времени t_p перед остановкой, чтобы распределение давление в пласте стабилизировалось.

Недостатки данного метода:

· сложно поддерживать постоянный дебит перед закрытием скважины;

· иногда требуется остановить скважину на короткий период, чтобы установить датчики в скважине;

· потеря добычи из-за простоя скважины при снятии КВД.

Основное преимущество — технически проще обеспечить постоянство дебита при снятии КВД после остановки (закрытия) добывающей скважины (q=0).

Исследования приемистости нагнетательной скважины— в момент времени

t = 0 скважина пускается в эксплуатацию с постоянным расходом флюида, нагнетаемого в пласт (рис. 1.2.3).

Исследование спада давления в нагнетательных скважинах

замер снижения давления после прекращения нагнетания жидкости в скважину (рис. 1.2.4).

Основное преимущество перед ГДИС в добывающих скважинах — скорость закачки жидкости легче контролировать, чем дебиты в добывающих скважинах.

Недостаток— анализ испытаний усложняется из-за:

· эффекта многофазного течения при закачке жидкости, отличной от пластового флюида;

· возможного образования трещин в призабойной зоне.

Исследования пластов по взаимодействию скважин:

· гидропрослушивание — при однократном возмущении;

· импульсный тест — при многократном циклическом возмущении.

Исследование взаимодействия скважин проводят с целью определения фильтрационных свойств продуктивных пластов. Для этого оборудуют несколько скважин одного блока/пласта глубинными манометрами с высокой чувствительностью. Перед проведением исследования все скважины данного блока продолжительное время должны эксплуатироваться с неизменным режимом. На одной из скважин (возбуждающей) производят смену режима эксплуатации (например, остановку скважины) (рис. 1.2.5).

Данный тип ГДИС позволяют определить:

· наличие гидродинамической связи между скважинами (участками пласта);

· фильтрационные характеристики продуктивного пласта в окрестности возмущающей и реагирующих скважин;

Наблюдательные скважины находятся в отдалении от возбуждающей скважины. Процесс перераспределения давления займет значительный период времени, прежде чем достигнет наблюдательной скважины.

Пластоиспытания— исследования, при которых используется устройство (пакер, клапан и манометр), опускаемое на забой скважины с помощью колонны буровых труб или НКТ. При помощи клапана, расположенного у основания колонны труб, вызывается приток флюида из пласта в скважину и замеряется давление (рис. 1.2.6).

Обычно этот вид исследований проводят на только что пробуренных поисковых или оценочных скважинах (обсаженных или необсаженных) с целью:

· определения природы пластового флюида;

· измерения продуктивности скважины;

· измерения пластового давления и температуры;

· получения образцов пластового флюида для РУТ анализа;

· получения информации о характеристиках коллектора;

· оценки эффективности завершения скважины (скин-фактор).

Период испытания очень короткий, т.к. скважина открывается и закрывается на забое

· снижается эффект ВСС. Дебит измеряется на поверхности — пластовый флюид проходит через сепаратор и определяются объемы добытых нефти, воды и газа.

В случае, если дебит замеряется на поверхности, интерпретация результатов испытаний пласта требует специальной методики, т.к. по мере повышения уровня жидкости в колонне труб изменяется дебит. Качество выполнения бурильных работ и операций по завершению скважины также могут влиять на результаты анализа.

Гидродинамические исследования скважины можно провести с помощью прибора, спускаемого в скважину на канате. Устройство (RFT — Repeat Formation Tester или MDT — Modular Dynamic Tester) спускается на нужную глубину и с помощью электрогидравлической системы прижимается пробоотборником к открытому стволу скважины. Если исследования проводятся в обсаженной скважине, то для установления сообщения между пластом и скважиной используются перфорационные заряды. Происходит отбор небольшого количества пластовой жидкости и замеряется давление (рис. 1.2.7).

RFT и MDT устройства применяются:

· для получения вертикального профиля давления;

· для отбора образцов пластового флюида;

· для оценки проницаемости.

В некоторых необсаженных скважинах бывает рискованно проводить данный тип исследований, существует опасность застревания и потери устройства.

Интерпретация результатов усложняется из-за наличия:

· радиально-сферического фильтрационного потока;

· короткого периода притока

ЗАКОН ДАРСИ

Эмпирический закон Дарси — первая попытка применить классические принципы гидродинамики к решению задачи течения жидкости в пористой среде:

где у = р — ρgD — потенциал; D — истинная вертикальная глубина; ρ — плотность жидкости. Потенциал у позволяет учесть гравитационные эффекты. При отсутствии гравитационных эффектов (линейный горизонтальный поток) уравнение

упрощается (рис. 1.3.1

Закон Дарси используется для определения проницаемости k, которая остается постоянной при условии:

· линейно-ламинарного и однофазного (насыщенность — 100%) течения;

· отсутствия химического взаимодействия между породой и пластовым флюидом;

Упражнение 1

Через два однородных образца пористой среды (рис. 1.3.2), содержащих глинистые частицы, с целью определения проницаемости k пропускали:

а) пресную воду при t = 20°С (вязкость = 1 спз) при перепаде давления р = 0.68 атм.с расходом Q = 2.88 х 10 -3 м 3 /сут,

б) соленую воду с вязкостью = 1.1 спз при той же разности давления, что и в случае (а) и с расходом Q = 10.468 х 10 -3 м 3 /сут.

Размеры образцов: длина L = 0.05 м, площадь поперечного сечения А = 5 х 10 -4 м 2 . Найти отношение проницаемостей для случаев (а) и (б).

Рассмотрим практическое использование закона Дарси на примере упрощенной модели нефтяного коллектора.

Допустим, коллектор представляет собой круговой однородный пласт, толщиной h и проницаемостью k, ограниченный сверху и снизу горизонтальными непроницаемыми барьерами. Давление на границе пласта (на расстоянии г_е от скважины) р_е, давление на забое p_w. Поровый объем заполнен нефтью (вязкость μ), за исключением того объема, который занимает связанная вода (в пластовых условиях — неподвижна) . Давление в пласте выше давления насыщения (нет свободной газовой фазы). Если скважина проперфорирована на весь продуктивный интервал h и пущена в эксплуатацию с постоянным дебитом q (в пластовых условиях), то в результате в пласте возникнет горизонтальный радиальный приток, направленный к скважине (рис. 1,3.3).

В результате получаем очень важное соотношение дебита q, депрессии p_e-p_w и свойств пласта;

(1.3.2)

Данное выражение известно как простейшая модель притока к скважине. Следует еще раз отметить, что дебит q и вязкость μ соответствуют пластовым условиям.

Упражнение 2

Определить давление на расстоянии 10 и 100 м от скважины при плоско-радиальном установившемся движении несжимаемой жидкости по линейному закону фильтрации, считая, что проницаемость пласта k = 0.5 дарси, мощность пласта h = 10 м, давление на забое скважины p_w = 80 атм, радиус скважины r_w = 12.4 см, коэффициент вязкости нефти μ₀ = 4 спз, объемный дебит скважины в пластовых условиях q= 229.885 м З /сут.

СЖИМАЕМОСТЬ

Сжимаемость с — относительное изменение объема флюида на единицу изменения давления (1.4.1). Единица измерения сжимаемости — величина обратная давлению (1/атм).

Изотермическая сжимаемость нефти выше давления насыщения. с_а всегда величина положительная, т.к. объем недонасыщенной жидкости уменьшается при увеличении давления. с₀ ределяется в лаборатории по экспериментальным данным или с помощью корреляции Трубэ. Для жидкости приблизительно можно считать постоянной, т.е. она не зависит от давления.

Общая сжимаемость системы с/(1.4.3), кроме изменения объема нефти, учитывает расширение пластовой воды и свободного газа, а также уменьшение объема пор (за счет сжатия породы).

Типичные величины сжимаемости для трех фазовых компонент, при среднем давлении p=136 атм.:

Сжимаемость газа на порядок выше, чем сжимаемость жидкости или породы. В газовых залежах принято считать, что –

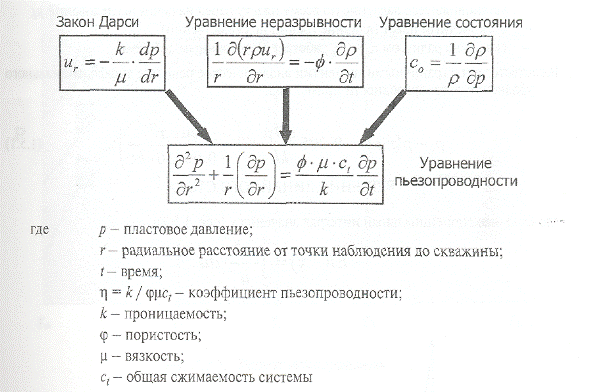
УРАВНЕНИЕ ПЬЕЗОПРОВОДНОСТИ

Математической основой для анализа ГДИС на неустановившихся режимах фильтрации является уравнение пьезопроводности в радиальных координатах, описывающее неустановившееся, однофазное, одномерное течение флюида в пористой среде.

Вывод уравнения пьезопроводности основывается на трех законах (рис. 1.5.1): Уравнение неразрывности (закон сохранения массы);

Рис. 1.5.1. Вывод уравнения пьезопроводности

Условные допущения, используемые при выводе уравнения:

· радиальный режим притока по всей эффективной толщине пласта;

· эффективная толщина пласта постоянна;

· q и k — постоянны (не зависят от давления);

· сжимаемость жидкости мала и постоянна;

· вязкость постоянна;

· маленький градиент давления

· гравитационные силы пренебрежимо малы.

Уравнение пьезопроводности выражает связь между пластовым давлением, временем и расстоянием от скважины до точки наблюдения. Если наложить граничные условия—

то можно решить уравнение и получить модель, характеризующую перераспределение давления в пласте.

При решении уравнения пьезопроводности обычно накладываются следующие граничные условия:

· установившееся давление по всему пласту перед началом исследований

· бесконечный пласт (влияние границ не существенно)

· скважина радиусом r_w « r_e работает с постоянным дебитом.

В соответствии с граничными условиями аналитическое решение дифференциального уравнения пьезопроводности примет вид:

РАДИУС ИССЛЕДОВАНИЙ

Решение уравнения пьезопроводности показывает, что перераспределение давления мгновенно распространяется по всему пласту. Но, с физической и практической точки зрения, существует какое-то расстояние r_inv от скважины, на котором изменение давления столь незначительно, что не может быть измерено.

r_inv — радиус исследований, определяет размер области вокруг скважины, которая влияет на результаты ГДИС (рис. 1.6.1).

Определение величины радиуса исследований зависит от того, что мы подразумеваем под минимальным измеримым сигналом ( р):

— Jones: r_inv — расстояние от скважины до определенной точки пласта, в которой изменение давления составляет 1% от изменения давления в скважине;

Poettmann: r_inv — расстояние от скважины до определенной точки пласта, в которой поток составляет 1% от потока в скважине;

— J. Lee и Muskat: r_inv — расстояние от скважины до определенной точки пласта, в которой скорость изменения давления максимальна (1.6.1).

(1.6.1)

Уравнения пьезопроводности при неустановившихся режимах

РЕЖИМЫ ТЕЧЕНИЯ

Радиальный режим течения — наиболее значимый режим с точки зрения интерпретации данных ГДИС. При радиальном режиме течения линии тока направлены к круговому цилиндру радиусом r (рис. 1.7.1 А).

Для скважины, вскрывающей пласт на всю продуктивную толщину, радиус цилиндра равен радиусу скважины r_w. Для скважины, вскрывающей только часть продуктивной толщины, радиальный приток относится только к начальному периоду исследования и только для той части пласта, в которой линии тока направлены горизонтально к скважине (рис. 1.7.1 Б).

Для скважин с ГРП и горизонтальных скважин эффективный радиус для радиального притока значительно больше, чем r_w. Приток к горизонтальной скважине в начальный период теста также является радиальным в вертикальной плоскости, перпендикулярной к стволу скважины (рис. 1.7.1 В, Г).

Сферический режим течения — линии тока сходятся в одной точке (рис. 1.7.2 А).

Сферический или полусферический режим притока случается в скважинах, несовершенных по степени вскрытия:

· частичное вскрытие (рис. 1.7.2 В);

· частичное проникновение (рис. 1.7.2 Б).

Скважины с трещиной ГРП могут иногда выходить на билинейный режим течения дополнительно к линейному режиму притока или вместо него (рис. 1.7.4 А).

Билинейный режим притока возникает в результате того, что:

· из-за перепада давления в самой трещине возникают параллельные линии тока в трещине, направленные к скважине;

· из-за перепада давления в пласте возникают параллельные линии тока, направленные из пласта к трещине.

Термин «билинейный режим течения» относится к случаю, когда существует одновременно два взаимно-перпендикулярных линейных притока (рис. 1.7.4 Б).

РЕЖИМЫ ПРИТОКА

Установившийся — распределение давления и дебита постоянно во времени. Данный тип притока возможен только при поддержке постоянного давления на границе пласта, т.е. при наличии большой газовой шапки, активной законтурной области или в случае проведения мероприятий по поддержанию пластового давления:

Неустановившийся — давление и/или дебит изменяются во времени, т.е. случай, когда перераспределение давления еще не достигло границ пласта и/или пока не проявляется влияние соседних скважин (рис. 1.8.1):

Псевдоустановившийся — профиль давления постоянен во времени. Давление на границе снижается. Данный режим притока характерен для изолированных пластов с непроницаемыми границами (рис. 1.8.2):

ГДИС почти всегда выполняются на неустановившемся режиме притока, даже если и начинает проявляться влияние границ пласта.

Этапы снижения давления при вводе скважины в эксплуатацию (рис. 1.8.3):

Переходный — давление на границе не влияет на распределение забойного давления.

Послепереходный — границы начинает влиять на распределение давления. Например, в условиях когда скважина работает в пласте нерегулярной формы (границы несимметричны).

Псевдоустановившийся — профиль давления не изменяется с течением времени.

MTR — средний период (бесконечный пласт).

LTR — поздний период (воздействие границ пласта).

Содержание

УРАВНЕНИЕ ПЬЕЗОПРОВОДНОСТИ
Добыча нефти и газа
Изучаем тонкости нефтегазового дела ВМЕСТЕ!
Понятия об упругом режиме пласта
🎦 Видео

Видео:Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

УРАВНЕНИЕ ПЬЕЗОПРОВОДНОСТИ

Рис. 1.5.1. Вывод уравнения пьезопроводности

Условные допущения, используемые при выводе уравнения:

· радиальный режим притока по всей эффективной толщине пласта;

· эффективная толщина пласта постоянна;

· q и k — постоянны (не зависят от давления);

· сжимаемость жидкости мала и постоянна;

· вязкость 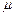постоянна;

· маленький градиент давления

· гравитационные силы пренебрежимо малы.

то можно решить уравнение и получить модель, характеризующую перераспределение давления в пласте.

При решении уравнения пьезопроводности обычно накладываются следующие граничные условия:

· установившееся давление по всему пласту перед началом исследований

· бесконечный пласт (влияние границ не существенно)

· скважина радиусом r_w « r_e работает с постоянным дебитом.

Видео:Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Добыча нефти и газа

Видео:Теория механизмов и машин. Лекция: динамика неустановившихся режимов работыСкачать

Изучаем тонкости нефтегазового дела ВМЕСТЕ!

Видео:Газодинамические исследованияСкачать

Понятия об упругом режиме пласта

При разработке нефтегазовых месторождений часто возникают неустановившиеся процессы, связанные с пуском или остановкой скважин, с изменением темпов отбора флюидов из скважин. Характер этих процессов проявляется в перераспределении пластового давления, в изменениях во времени скоростей фильтрации, дебитов скважин и т.д. Особенности данных процессов зависят от упругих свойств пластов и жидкостей, т.е. основная форма пластовой энергии — энергия упругой деформации жидкостей и материала пласта.

Упругий режим характеризуется двумя особенностями:

* неустановившимися процессами перераспределения давления в пласте;

* изменением упругого запаса жидкости в пласте.

При упругом режиме движение возникает в призабойной зоне в начале эксплуатации скважины за счет использования потенциальной энергии упругой деформации пласта и жидкости и только через некоторое время оно распространяется на более отдалённые области.

При снижении пластового давления объём сжатой жидкости увеличивается, а объём порового пространства сокращается за счет расширения материала пласта. Всё это способствует вытеснению жидкости из пласта в скважину.

В ряде случаев приток жидкости поддерживается за счет напора воды, поступающей извне. Такой режим называется упруговодонапорным.

Если залежи нефти ограничены либо зонами выклинивания, либо экранами, то режим называется замкнуто-упругим. В начальной стадии разработки такой залежи до тех пор, пока пластовое давление не снизилось ниже давления насыщения, имеет место замкнуто-упругий режим фильтрации.

Если вытеснение жидкости из пласта происходит не под действием преобладающего влияния упругости пласта и жидкости, то упруговодонапорный режим переходит в жестко-водонапорный режим. При этом режиме влияние упругости пласта и жидкости на фильтрационный поток хотя и не прекращается, но заметно не проявляется.

Неустановившиеся процессы протекают тем быстрее, чем больше коэффициент проницаемости пласта k, и тем медленнее, чем больше вязкость жидкости m и коэффициенты объёмной упругости жидкости и пласта.

4.1.2. Основные параметры теории упругого режима

Важнейшими параметрами теории упругого режима являются коэффициенты объёмной упругости жидкости и пласта.

Коэффициент объёмной упругости жидкости bж характеризует податливость жидкости изменению её объёма и показывает, на какую часть первоначального объёма изменяется объём жидкости при изменении давления на единицу

, (4.1)

где tж — объём жидкости; знак минус указывает на то, что объём tж увеличивается с уменьшением давления; bж нефти находится в пределах (7-30)10-10м2/н; bж воды находится в пределах (2,7-5)10-10м2/н.

Коэффициент объёмной упругости пласта определяется по формуле

, (4.2)

где tп — объём пласта; m — пористость; bС слабо и сильно сцементированных горных пород находится в пределах (0,3-2)10-10м2/н.

Большое значение в практике добычи нефти и подсчета её запасов имеет величина упругого запаса выделенной области пласта, соответствующая заданному падению давления. По Щелкачеву упругий запас — это количество жидкости, высвобождающейся в процессе отбора из некоторой области пласта при снижении пластового давления до заданной величины, если высвобождение происходит за счет объёмного расширения жидкости и уменьшения порового пространства пласта.

Обозначая упругий запас через Dtз , получаем по определению

Dtз = bжt0жDр + bсt0Dр, (4.3)

где t0ж — объём жидкости, насыщающей элемент объёма пласта t0 при начальном давлении р0; Dр — изменение давления.

Так как t0ж = mt0, то

Здесь b* = mbж + bс — коэффициент упругоёмкости пласта, показывающий долю объема жидкости от выделенного элемента объема пласта, высвобождающейся из элемента пласта при снижении давления на единицу.

Вскрытие пласта и изменение режима работы скважины вызывает возмущение в пласте. От источника возмущения оно передаётся во все стороны пласта с какой-то скоростью. Скорость распространения изменения пластового давления характеризуется коэффициентом пьезопроводности пласта

. (4.5)

Здесь L, T –размерности длины и времени.

В коллекторах – 1000см2/с £ k £ 50000см2/c или 0.1м2/с £k £5м2/c.

Степень нестационарности процессов определяется безразмерными параметрами Фурье:

для призабойной зоны — ; (4.6)

для всего пласта , (4.7)

4.1.3. Дифференциальное уравнение неустановившейся фильтрации упругой жидкости (уравнение пьезопроводности)

Считаем, что течение происходит по закону Дарси, и уравнение состояния упругой жидкости в линеаризованной постановке, которое получим из соотношения (2.27) разложением экспоненты в ряд Тейлора, имеет вид

, (4.8)

а также изменение пористости в зависимости от давления, полученное линеаризацией соотношения (2.34), описывается зависимостью

. (4.9)

Из (4.9) и очевидного соотношения имеем следующее дифференциальное уравнение для пористости, при пренебрежении членом, содержащим произведение bжbс

. (4.10)

В то же время из общего уравнения фильтрации (2.8) .

Приравнивая правые части, с учетом выражения для потенциала , и пренебрегая членом, содержащим (р-р0)2, получим

. (4.11)

Уравнение типа (4.11) известно под названием уравнения теплопроводности, а в теории фильтрации называется уравнением пьезопроводности. По аналогии с уравнением теплопроводности коэффициент k характеризует быстроту распределения давления в пласте и носит название коэффициент пьезопроводности. Само уравнение (4.11) позволяет определить поле давления при нестационарных процессах в пласте с упругим режимом.

4.1.4. Приток к скважине в пласте неограниченных размеров

4.1.4.1. Вывод основного уравнения упругого режима

Считаем пласт упругим, горизонтальным и большой протяженности и в нём имеется одна скважина, тогда движение жидкости в пласте можно считать плоскорадиальным к точечному стоку (эксплуатационная скважина) или от точечного источника (нагнетательная скважина).

Рассмотрим процесс перераспределения давления при неустановившемся, плоском радиальном движении жидкости. Для этого запишем уравнение пьезопроводности в цилиндрической системе координат

. (4.12)

Предположим, что возмущение вызвано мгновенным стоком, существовавшим в момент t = t/ . Для этого случая решение уравнения (4.12) имеет вид

, (4.13)

где А и С — некоторые постоянные.

Найдём значения постоянных. Для этого будем считать, что в момент времени t = t/ давление в пласте было р = рк = const. Тогда при r > 0 и при t = t/ второй член правой части обращается в неопределённость типа ¥/¥ и определяется по правилу Лопиталя, что даёт С = рк. Таким образом,

. (4.14)

Для определения коэффициента А воспользуемся соотношением (4.4) для определения объёма высвобождающейся жидкости для случая кольцевого элемента пласта с внутренним радиусом r, толщиной h и шириной dr, а также учтем падение давления Dр = p0 — p по (4.14):

dtз = b*Dрdt0 = . (4.15)

После интегрирования (4.15) в пределах от 0 до ¥ получим объём жидкости t2 , выделившейся из всего пласта и, следовательно, определим коэффициент А:

. (4.16)

Таким образом в случае скважины, введенной в неограниченный пласт в некоторый (начальный) момент времени и действующей мгновенно, изменение давления во времени определяется соотношением:

. (4.17)

Если скважина была введена в некоторый момент времени и действовала непрерывно с постоянным дебитом Q = Q0 в течение времени dt/, то за этот промежуток времени через сток выделяется из пласта объём

dt2 = Qdt/ и, следовательно, из (4.17) следует

. (4.18)

Интеграл правой части носит название интегрально-показательной функции

и с учетом данного обозначения решение для изменения давления запишется в виде

. (4.19)

Формула (4.19) является основной формулой теории упругого режима пласта.

Рис. 4.1. График интегрально — показательной функции

Интегрально-показательная функция имеет вид (рис.4.1) и обладает следующими свойствами:

* -Ei(-u) изменяется от 0 до ¥ при изменении аргумента от 0 до ¥;

* функция -Ei(-u) представляется в виде сходящегося ряда

(4.20)

Для малых значений u

, (4.21)

с погрешностью, не превышающей 0,25% при u

. (4.22)

С учетом соотношения (4.21) основное уравнение (4.19) перепишется в виде, которое более известно под названием уравнение кривой восстановления давления (КВД)

. (4.23)

Рис. 4.2. Пьезометрические кривые при пуске скважины в бесконечном пласте с постоянным дебитом

Полученную зависимость можно использовать при числе Фурье с погрешностью, не превышающей 0,6%. Практически это означает, что уже через 1 с после пуска скважины расчеты забойного давления, выполненные по формуле (4.23), будут иметь погрешность не превышающую 0,6%. Формулу (4.23) можно использовать и для расчета падения давления в конечном пласте, а именно, погрешность расчета давления при этом не превышает 1%, если rк > 1000rc и fo

Рассмотрим пьезометрические кривые для бесконечного пласта, который эксплуатируется скважиной радиуса rc c постоянным дебитом Q0 (рис.4.2). Для точек вблизи забоя можно пользоваться формулой (4.23), а дифференцируя её по координате r, найдём градиент давления

Из этой формулы следует, что градиент давления для значений r, удовлетворяющих неравенству r2

4.1.4.2. Анализ основной формулы теории упругого режима

Основная формула (4.19) или (4.23) строго говоря справедлива лишь для точечного стока, т.е. при rс=0. Практические расчеты показывают, что ей можно пользоваться даже для укрупнённых скважин (rс

1км) и нельзя использовать только в первые доли секунды после пуска скважины. Если скважина укрупнённая, то формула (4.23) может дать большую погрешность лишь вблизи от её стенки (контура). Чем дальше отстоит от этого контура точка, в которой определяется давление, и чем больше времени прошло с момента пуска укрупнённой скважины, тем меньше погрешность.

Анализ формулы (4.23) показывает, что вскоре после пуска скважины вокруг неё начинает непрерывно увеличиваться область пласта (рис.4.2), в которой для каждого момента времени давление распределяется так, как и при установившемся движении, т.е. давление оказывается квазиустановившимся и пьезометрические кривые будут кривыми логарифмического типа.

Из (4.23) следует, что градиент давления, расход жидкости через любую цилиндрическую поверхность радиусом r и скорость фильтрации определяются соотношениями:

(4.24)

Из данных соотношений следует, что стационарная скорость достигается очень быстро на небольших расстояниях от скважины, так как значение коэффициента пьезопроводности велико.

4.1.4.3. Приток к скважине в пласте конечных размеров в условиях упруго-водонапорного и замкнуто- упругого режима

Круглый горизонтальный пласт с открытой внешней границей

Рис. 4.3. . Пьезометрические кривые при пуске скважины в конечном пласте

с открытой внешней границей:

а — с постоянным дебитом;

b — с постоянным забойным давлением рс

Постоянный дебит. Пусть пласт имеет внешнюю границу радиусом rк, через которую может поступать вода при истощении упругого запаса. В центре пласта имеется скважина радиусом rс, которая мгновенно запускается в эксплуатацию с постоянным дебитом Q0. Перед пуском скважины давление в пласте было рк.

Для определения давления используем полученную ранее зависимость

, (4.19)

для неограниченного пласта и формулу Дюпюи

(4.25)

для установившегося плоскорадиального потока. В результате совместного решения данных зависимостей получим следующую приближённую формулу

, (4.26)

Рис. 4.4. Изменение дебита скважины с течением времени при постоянном забойном давлении рс

где ру — установившееся давление в любой точке пласта или в реагирующей бездействующей скважине (давление ру соответствует времени t = ¥ или Fo = ¥ ).

Изменение пьезометрической кривой в различные моменты времени после пуска скважины с постоянным дебитом в пласте с круговым контуром питания показано на рис.4.3а.

Постоянное забойное давление. На рис 4.3b изображена в различные моменты времени пьезометрическая кривая после пуска возмущающей скважины с постоянным забойным давлением, на рис.4.4 — изменение дебита скважины с течением времени.

Круглый горизонтальный пласт с закрытой внешней границей

Рис. 4.4. Пьезометрические кривые при пуске скважины в конечном пласте с закрытой внешней границей при

Постоянный дебит. Будем считать дебит скважины постоянным. Пьезометрические кривые падения давления для разных моментов времени показаны на рис. 4.4. С некоторого момента смещение во времени пьезометрической кривой для закрытого пласта происходит так, что все точки её опускаются на одно и тоже расстояние d, т.е. во всех точках пласта давление падает с одной скоростью.

Из рассмотрения рис. 4.3, 4.4. видно, что в условиях упругого режима процесс перераспределения давления, а значит, и процесс взаимодействия скважин развивается постепенно, если же и наблюдается аномально быстрое взаимодействие скважин, то это можно объяснить неоднородностью пластов и их анизотропией.

Кроме того, при пуске или остановке скважины давление вначале меняется быстро, а затем темп изменения давления замедляется.

Если скважина действовала с постоянным дебитом при установившимся потоке и в некоторый момент времени она останавливается, то начинается процесс восстановления давления. Уровень жидкости в скважине начинает подыматься.

Для расчета используются полученные выше формулы для возмущающей скважины, но вместо данных понижения давления в пласте надо подставить данные повышения давления после остановки скважины.

Рис. 4.6. Пьезометрические кривые при пуске скважины в конечном пласте с закрытой внешней границей при постоянном забойном давлении

Рис. 4.7. Изменение дебита Q (кр.1) скважины и суммар-ной добычи Qcp (кр.2) с течением времени t

Постоянное забойное давление. Объемный дебит возмущающей скважины определяется по формуле

(4.27)

а объем жидкости tж, добытой из скважины (в пластовых условиях) за время t с момента пуска скважины равен

При больших параметрах Фурье fo объем Qж оказывается равным упругому запасу жидкости в закрытом пласте

На рис. 4.6 показана пьезометрическая кривая для нескольких моментов времени в закрытом пласте, а на рис. 4.7 изображены две кривые: одна из них характеризует падение дебита скважины с постоянным забойным давлением (кр. 1); другая — рост суммарной добычи жидкости tж (кр.2).

4.1.4.4. Определение коллекторских свойств пласта по данным исследования скважин нестационарными методами

Различают две группы гидродинамических методов: при установившихся и неустановившихся режимах. Первые связаны с теорией одномерного потенциального течения, а вторые — с теорией упругого режима. После пуска или остановки скважины происходит перераспределение давления, которое можно снять и получить кривую восстановления (КВД) или стабилизации (КСД) давления. На форму данных кривых влияют коллекторские свойства, что дает возможность определения таких параметров как проницаемость и пьезопроводность.

Наиболее распространен метод определения коллекторских свойств по данным о восстановлении забойного давления (КВД) в остановленных скважинах в полулогарифмических координатах (Dр, lnt) на основе зависимости (4.30), записанной относительно забоя скважины в виде

(4.34)

Уравнение (4.34) можно рассматривать как уравнение изменения забойного давления после остановки скважины, работающей до этого с постоянным дебитом Q.

Рис. 4.8. Кривая КВД

Уравнение (4.34) представляет собой прямую (рис. 4.8) в координатах Dрс-lnt, а коэффициент i определяется как тангенс угла её наклона j к оси времени и коэффициент А — как отрезок оси давления, отсекаемый продолжением прямой.

По известным коэффициентам можно определить коллекторские свойства пласта:

· по коэффициенту i определяют гидропроводность пласта

. (4.35)

· Если известна вязкость жидкости в пластовых условиях m и толщина пласта h, то из последней формулы находится коэффициент проницаемости пласта:

. (4.36)

· По известному угловому коэффициенту i = tgj и радиусу rc скважины из коэффициента А можно определить коэффициент пьезопроводности пласта.

Область применения указанных приемов интерпретации результатов исследования нефтяных скважин ограничивается условиями, при которых справедлива формула (4.34), а именно: скважина рассматривается как сток постоянной интенсивности в бесконечном однородном пласте , и возможна мгновенная остановка притока флюида в скважину.

В случае ограниченого пласта, когда изменение давления, вызванное закрытием скважины, доходит до его границы, КВД начинает искажаться, а через достаточно большое время выходит на горизонтальную асимптоту, соответствующую стационарному распределению давления. Поэтому длина прямолинейного участка на кривой КВД ограничена.

Кроме того, в реальных условиях скважину нельзя остановить мгновенно. После её закрытия на устье приток флюида из пласта продолжается ещё некоторое время из-за упругости жидкостей и газов, заполняющих скважину. Время выхода на асимптоту должно, очевидно, превышать время дополнительного притока. Поэтому возможны условия, при которых прямолинейный участок на КВД появляется через значительный промежуток времени, либо даже вообще отсутствует.

На форму КВД сказывается также несовершенство скважины и возможное нарушение закона Дарси у стенок скважины. В этом случае необходимо решение более сложного уравнения пьезопроводности с нелинейными членами и использование приближенных методов расчета коллекторских свойств.

Твердотопливные котлы в Украине котлы в Украине

Полное описание первых признаков и выраженных симптомов при гепатите В здесь