Уравнения переходных токов и напряжений (2 видео)

Уравнения переходных токов и напряжений

При всех изменениях в электрической цепи: включении, выключении, коротком замыкании, колебаниях величины какого-либо параметра и т.п. – в ней возникают переходные процессы, которые не могут протекать мгновенно, так как невозможно мгновенное изменение энергии, запасенной в электромагнитном поле цепи. Таким образом, переходный процесс обусловлен несоответствием величины запасенной энергии в магнитном поле катушки и электрическом поле конденсатора ее значению для нового состояния цепи.

При переходных процессах могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания, которые могут нарушить работу устройства вплоть до выхода его из строя. С другой стороны, переходные процессы находят полезное практическое применение, например, в различного рода электронных генераторах. Все это обусловливает необходимость изучения методов анализа нестационарных режимов работы цепи.

Основные методы анализа переходных процессов в линейных цепях:

Классический метод, заключающийся в непосредственном интегрировании дифференциальных уравнений, описывающих электромагнитное состояние цепи.
Операторный метод, заключающийся в решении системы алгебраических уравнений относительно изображений искомых переменных с последующим переходом от найденных изображений к оригиналам.
Частотный метод, основанный на преобразовании Фурье и находящий широкое применение при решении задач синтеза.
Метод расчета с помощью интеграла Дюамеля, используемый при сложной форме кривой возмущающего воздействия.
Метод переменных состояния, представляющий собой упорядоченный способ определения электромагнитного состояния цепи на основе решения системы дифференциальных уравнений первого прядка, записанных в нормальной форме (форме Коши).

Классический метод расчета

Классический метод расчета переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений, описывающих изменения токов и напряжений на участках цепи в переходном процессе.

В общем случае при использовании классического метода расчета составляются уравнения электромагнитного состояния цепи по законам Ома и Кирхгофа для мгновенных значений напряжений и токов, связанных между собой на отдельных элементах цепи соотношениями, приведенными в табл. 1.

Таблица 1. Связь мгновенных значений напряжений и токов на элементах электрической цепи

;

при наличии магнитной связи с катушкой, обтекаемой током ,

;

Для последовательной цепи, содержащей линейные резистор R, катушку индуктивности L и конденсатор С, при ее подключении к источнику с напряжением u (см. рис. 1) можно записать

Резистор (идеальное активное сопротивление)

Катушка индуктивности (идеальная индуктивность)

Конденсатор (идеальная емкость)

(1)

Подставив в (1) значение тока через конденсатор

получим линейное дифференциальное уравнение второго порядка относительно

В общем случае уравнение, описывающее переходный процесс в цепи с n независимыми накопителями энергии, имеет вид:

(2)

где х – искомая функция времени (напряжение, ток, потокосцепление и т.п.); — известное возмущающее воздействие (напряжение и (или) ток источника электрической энергии); — к-й постоянный коэффициент, определяемый параметрами цепи.

Порядок данного уравнения равен числу независимых накопителей энергии в цепи, под которыми понимаются катушки индуктивности и конденсаторы в упрощенной схеме, получаемой из исходной путем объединения индуктивностей и соответственно емкостей элементов, соединения между которыми являются последовательными или параллельными.

В общем случае порядок дифференциального уравнения определяется соотношением

(3)

где и — соответственно число катушек индуктивности и конденсаторов после указанного упрощения исходной схемы; — число узлов, в которых сходятся только ветви, содержащие катушки индуктивности (в соответствии с первым законом Кирхгофа ток через любую катушку индуктивности в этом случае определяется токами через остальные катушки); — число контуров схемы, ветви которых содержат только конденсаторы (в соответствии со вторым законом Кирхгофа напряжение на любом из конденсаторов в этом случае определяется напряжениями на других).

Наличие индуктивных связей на порядок дифференциального уравнения не влияет.

Как известно из математики, общее решение уравнения (2) представляет собой сумму частного решения исходного неоднородного уравнения и общего решения однородного уравнения, получаемого из исходного путем приравнивания его левой части к нулю. Поскольку с математической стороны не накладывается каких-либо ограничений на выбор частного решения (2), применительно к электротехнике в качестве последнего удобно принять решение , соответствующее искомой переменной х в установившемся послекоммутационном режиме (теоретически для ).

Частное решение уравнения (2) определяется видом функции , стоящей в его правой части, и поэтому называется принужденной составляющей. Для цепей с заданными постоянными или периодическими напряжениями (токами) источников принужденная составляющая определяется путем расчета стационарного режима работы схемы после коммутации любым из рассмотренных ранее методов расчета линейных электрических цепей.

Вторая составляющая общего решения х уравнения (2) – решение (2) с нулевой правой частью – соответствует режиму, когда внешние (принуждающие) силы (источники энергии) на цепь непосредственно не воздействуют. Влияние источников проявляется здесь через энергию, запасенную в полях катушек индуктивности и конденсаторов. Данный режим работы схемы называется свободным, а переменная — свободной составляющей.

В соответствии с вышесказанным, общее решение уравнения (2) имеет вид

(4)

Соотношение (4) показывает, что при классическом методе расчета послекоммутационный процесс рассматривается как наложение друг на друга двух режимов – принужденного, наступающего как бы сразу после коммутации, и свободного, имеющего место только в течение переходного процесса.

Необходимо подчеркнуть, что, поскольку принцип наложения справедлив только для линейных систем, метод решения, основанный на указанном разложении искомой переменной х, справедлив только для линейных цепей.

Начальные условия. Законы коммутации

В соответствии с определением свободной составляющей в ее выражении имеют место постоянные интегрирования , число которых равно порядку дифференциального уравнения. Постоянные интегрирования находятся из начальных условий, которые принято делить на независимые и зависимые. К независимым начальным условиям относятся потокосцепление (ток) для катушки индуктивности и заряд (напряжение) на конденсаторе в момент времени (момент коммутации). Независимые начальные условия определяются на основании законов коммутации (см. табл. 2).

Таблица 2. Законы коммутации

Первый закон коммутации (закон сохранения потокосцепления)

Магнитный поток, сцепленный с катушками индуктивности контура, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: .

Второй закон коммутации (закон сохранения заряда)

Электрический заряд на конденсаторах, присоединенных к любому узлу, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: .

Доказать законы коммутации можно от противного: если допустить обратное, то получаются бесконечно большие значения и , что приводит к нарушению законов Кирхгофа.

На практике, за исключением особых случаев (некорректные коммутации), допустимо использование указанных законов в другой формулировке, а именно:

первый закон коммутации – в ветви с катушкой индуктивности ток в момент

коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: .

второй закон коммутации – напряжение на конденсаторе в момент

коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: .

Необходимо подчеркнуть, что более общей формулировкой законов коммутации является положение о невозможности скачкообразного изменения в момент коммутации для схем с катушкой индуктивности – потокосцеплений, а для схем с конденсаторами – зарядов на них. В качестве иллюстрации сказанному могут служить схемы на рис. 2, переходные процессы в которых относятся к так называемым некорректным коммутациям (название произошло от пренебрежения в подобных схемах малыми параметрами, корректный учет которых может привести к существенному усложнению задачи).

Действительно, при переводе в схеме на рис. 2,а ключа из положения 1 в положение 2 трактование второго закона коммутации как невозможность скачкообразного изменения напряжения на конденсаторе приводит к невыполнению второго закона Кирхгофа . Аналогично при размыкании ключа в схеме на рис. 2,б трактование первого закона коммутации как невозможность скачкообразного изменения тока через катушку индуктивности приводит к невыполнению первого закона Кирхгофа . Для данных схем, исходя из сохранения заряда и соответственно потокосцепления, можно записать:

Зависимыми начальными условиями называются значения остальных токов и напряжений, а также производных от искомой функции в момент коммутации, определяемые по независимым начальным условиям при помощи уравнений, составляемых по законам Кирхгофа для . Необходимое число начальных условий равно числу постоянных интегрирования. Поскольку уравнение вида (2) рационально записывать для переменной, начальное значение которой относится к независимым начальным условиям, задача нахождения начальных условий обычно сводится к нахождению значений этой переменной и ее производных до (n-1) порядка включительно при .

Пример. Определить токи и производные и в момент коммутации в схеме на рис. 3, если до коммутации конденсатор был не заряжен.

В соответствии с законами коммутации

и .

На основании второго закона Кирхгофа для момента коммутации имеет место

и .

Для известных значений и из уравнения

определяется .

Значение производной от напряжения на конденсаторе в момент коммутации (см. табл. 1)

Корни характеристического уравнения. Постоянная времени

Выражение свободной составляющей общего решения х дифференциального уравнения (2) определяется видом корней характеристического уравнения (см. табл. 3).

Таблица 3. Выражения свободных составляющих общего решения

Вид корней характеристического уравнения

Выражение свободной составляющей

Корни вещественные и различные

Корни вещественные и

Пары комплексно-сопряженных корней

Необходимо помнить, что, поскольку в линейной цепи с течением времени свободная составляющая затухает, вещественные части корней характеристического уравнения не могут быть положительными.

При вещественных корнях монотонно затухает, и имеет место апериодический переходный процесс. Наличие пары комплексно сопряженных корней обусловливает появление затухающих синусоидальных колебаний (колебательный переходный процесс).

Поскольку физически колебательный процесс связан с периодическим обменом энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, комплексно-сопряженные корни могут иметь место только для цепей, содержащих оба типа накопителей. Быстроту затухания колебаний принято характеризовать отношением

которое называется декрементом колебания, или натуральным логарифмом этого отношения

называемым логарифмическим декрементом колебания, где .

Важной характеристикой при исследовании переходных процессов является постоянная времени t , определяемая для цепей первого порядка, как:

где р – корень характеристического уравнения.

Постоянную времени можно интерпретировать как временной интервал, в течение которого свободная составляющая уменьшится в е раз по сравнению со своим начальным значением. Теоретически переходный процесс длится бесконечно долго. Однако на практике считается, что он заканчивается при

Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.

Содержание

Расчеты переходных процессов в электрических сетях
Оглавление
Зачем вообще что-то рассчитывать в энергетике?
Переходные процессы – это…
Переходные процессы и режим реального времени
Нельзя просто так взять и рассчитать переходный процесс
Куда и как запустить модель?
Управление по управлению всеми управлениями
Все уже сделано до нас
Переходный, принужденный и свободный режим в электрической цепи
🔥 Видео

Видео:Расчет переходного процесса через ДИФФЕРЕНЦИАЛЬНОЕ уравнение по законам Кирхгофа│Классический методСкачать

Расчеты переходных процессов в электрических сетях

Энергетика – обширная сфера деятельности, и расчеты в ней производятся разные: расчет рентабельности строительства новых станций, расчет перенапряжений, расчет оставшегося времени до конца рабочего дня в пятницу вечером. Все эти темы в одной статье не уместить, поэтому сконцентрируюсь на той, которой занимался в течение последних лет, – расчеты переходных процессов в электрических сетях. Кому интересно, что это такое и как оно происходит в современном мире, – прошу под кат.

Зачем вообще что-то рассчитывать в энергетике?

Причины довольно стандартны для любой технической/инженерной сферы: экономия, безопасность, нормативы и прочие банальности. Несколько примеров:

Чем точнее мы знаем, какие перенапряжения могут возникнуть, тем меньше денег можно затратить на изоляционный материал, имеющий достаточный запас прочности.
Чем больше информации имеется о резонансных частотах в сети, тем точнее можно настроить систему управления и эффективнее справляться с воздействием внешних факторов.
Чем детальнее изучено поведение оборудования в тех или иных режимах, тем проще соблюсти нормативы, пройти сертификацию или приёмку.
И т. д.
И т. п.

Что объединяет приведенные выше примеры? То, каким образом можно получить всю эту интересующую нас информацию. Те, кто помнит название статьи, уже догадались: это можно сделать, рассчитав переходные процессы.

Впрочем, если у вас есть деньги и время для проведения экспериментов, то можно одними расчетами не ограничиваться, ведь теория – это хорошо, а теория, подкрепленная экспериментами, – еще лучше. Правда это может быть долго, дорого и не всегда возможно, ведь ставить эксперименты на работающей энергосистеме – это, выражаясь местным сленгом, сродни запуску тестов на продакшн сервере – если что-то пойдет не так, то мало не покажется.

Видео:Пример 7 | Классический метод расчета цепи 1-го порядка с конденсаторомСкачать

Переходные процессы – это…

Если по-простому, переходный процесс – это когда токи и напряжения в электрической сети изменяются во времени вследствие различных событий, таких как короткие замыкания, отключения выключателей, удары молнии и проч. и проч. Переходные процессы – явления чаще всего временные. В электроэнергетике они могут длиться как нано- и микросекунды (переключение транзисторов, удары молнии), так и несколько минут или часов (межсистемные колебания, электромагнитные бури).

Рассчитать переходный процесс – значит узнать, как именно изменяются токи и напряжения.

Переходные процессы обычно плавно перетекают в установившиеся. В установившемся процессе, если опять же по-простому, величины токов и напряжений постоянны. «А как же напряжение в розетке, которое меняется 50 раз в секунду?» – спросите вы. В принципе, это тоже можно рассматривать как непрекращающийся переходный процесс, но если амплитуда, частота и фаза синусоидального сигнала постоянны, то гораздо удобнее рассматривать как установившийся. Для этого существуют свои методы, но об этом как-нибудь в другой раз.

Вот, например, напряжения на конденсаторе при подключении его к трехфазной сети 10 кВ (если что, конденсаторов на самом деле три – по одному на каждую фазу):

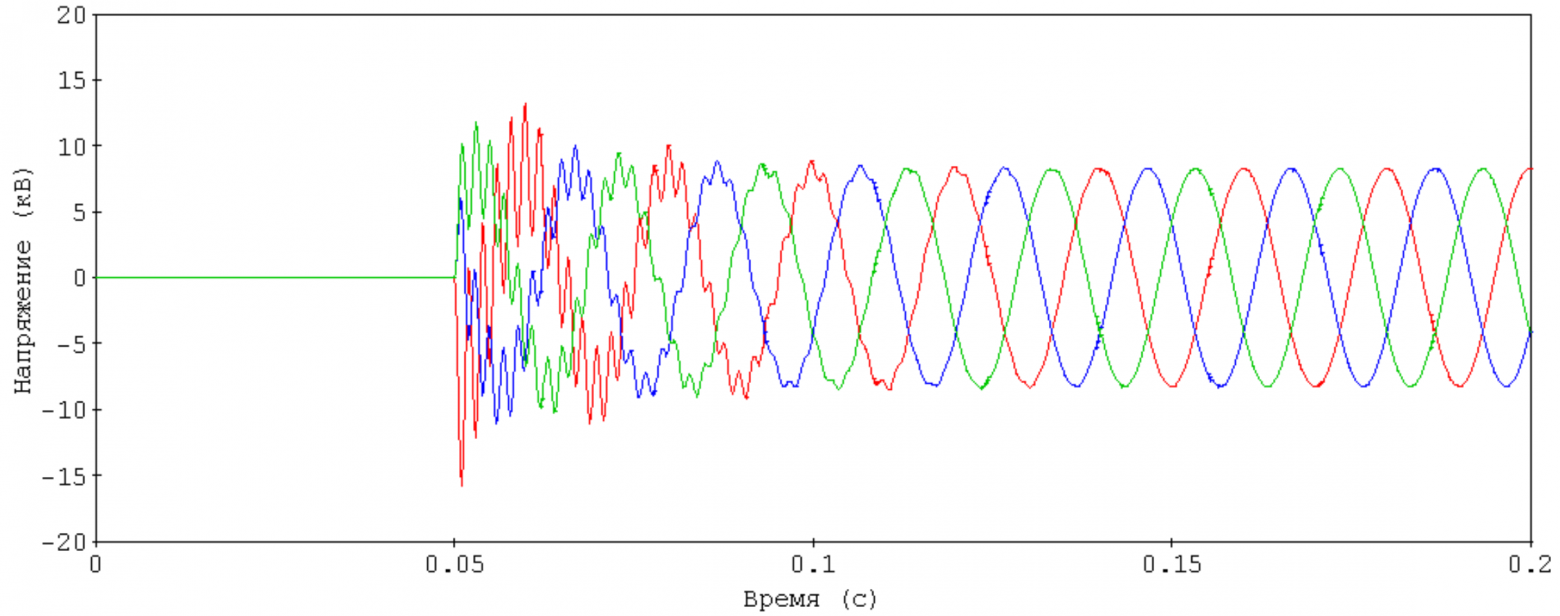
Где-то сейчас замигали лампочки

Вопрос: когда начинается переходный процесс?

Вопрос со звездочкой: когда заканчивается переходный процесс и начинается установившийся?

Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Переходные процессы и режим реального времени

Есть еще одна область применения расчетов переходных процессов – это расчеты в реальном времени. Если обычно все гонятся за уменьшением времени расчетов, то здесь, наоборот, очень важно, чтобы расчет одной секунды проходил ровно за одну секунду. Это применяется, например, для прототипирования, тестирования и отладки устройств, предназначенных для взаимодействия с реальным миром: систем управления, защиты и т.д.

Поясню на примере: система управления электростанцией знает, что для реакции на событие X электростанции понадобится две секунды, а на событие Y – три. Чтобы дебажить эту систему управления, её подключают не к реальной электростанции, а к так называемому симулятору, имитирующему поведение электростанции. Симулятор в реальном времени рассчитывает переходные процессы, которые происходили бы в электростанции, и ведет себя соответствующе: отвечает на событие X за две секунды, а на Y – за три вне зависимости от количества ядер процессора и тактовой частоты. Система управления при этом думает, что работает с реальной электростанцией.

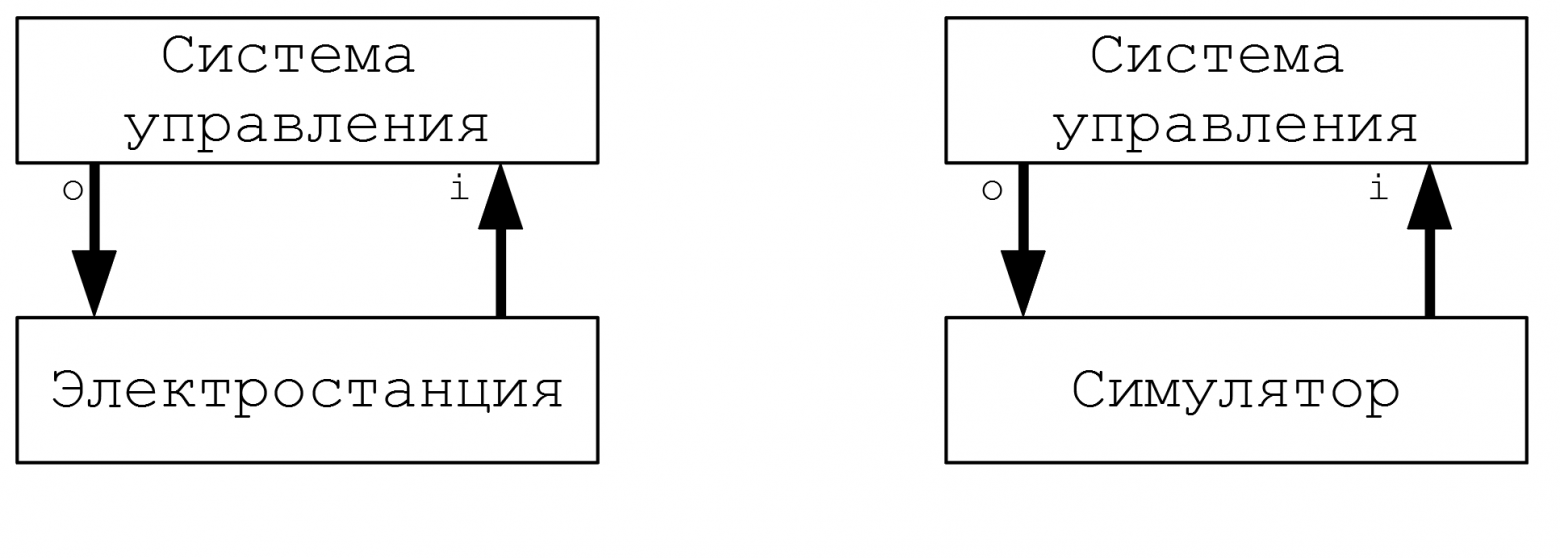
Слева: система управления и электростанция дружно работают на благо родины.
Справа: ничего не подозревающая система управления коварно обманута и подключена к симулятору

Видео:Пример 6 | Классический метод расчета цепи первого порядка с конденсаторомСкачать

Нельзя просто так взять и рассчитать переходный процесс

В рассчитываемой электрической сети могут иметься тысячи различных компонентов, поэтому ручной расчет переходных процессов практически неприменим к реальным задачам в электроэнергетике – все считается на компьютере. Расчеты переходных процессов в реальном времени производить вручную еще сложнее, ведь вам понадобится еще и секундомер.

В начале расчета стоит определиться, какая от него требуется информация. Например, нам нужно узнать перенапряжения, возникающие при коротком замыкании в преобразователе постоянного тока на морской ветроэлектростанции. С типом расчетов всё и так понятно из названия статьи – нужно рассчитывать переходные процессы.

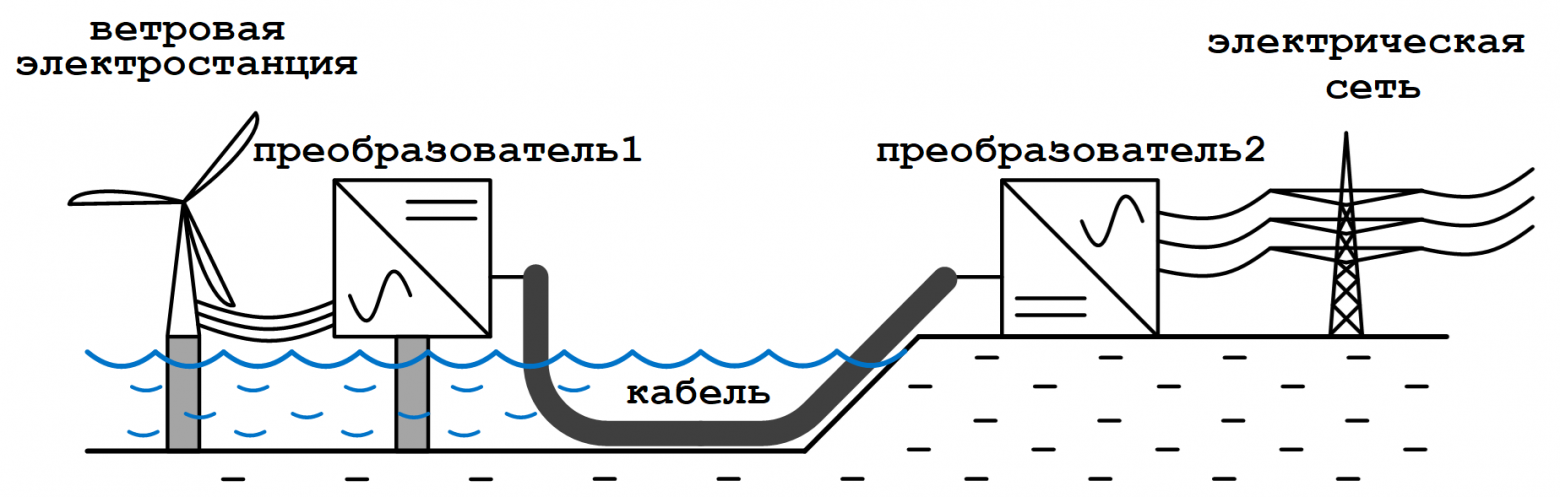
Вот так схематично эта система может выглядеть

Затем нужно разработать математическую модель рассчитываемой системы: ветровой электростанции, преобразователей, кабеля и прилегающей электрической сети. Этот этап может быть довольно сложным, ведь не всегда сразу ясно, насколько детальны должны быть модели. Чем больше деталей, тем точнее результат, но тем больше времени надо потратить на расчеты. Никто не любит долго ждать, поэтому приходится искать компромисс. Часто для удовлетворительной точности требуются многие десятки дифференциальных и не очень уравнений для каждого устройства.

Как только модель системы у нас появилась, можно запустить её в солвер (об этом чуть дальше), задать начальные условия и все рассчитать. Как происходит типичный расчет:

Интересующий период времени разбивается на отрезки с шагом интегрирования ∆t. Чем меньше шаг интегрирования, тем медленнее процесс расчета и точнее результаты. Часто используются величины ∆t от единиц до десятков микросекунд.
Величины токов и напряжений в момент времени (t-∆t) используются для расчета величин на следующем моменте времени (t).
Начальные условия, т. е. начальные величины токов и напряжений, находятся из предположения, что в момент времени t=0 был установившийся режим.

Когда расчет закончен, можно использовать результаты по назначению (ну или обнаружить перенапряжения в миллиарды вольт и понять, что кто-то перепутал плюс с минусом).

Видео:Резонансы токов и напряженийСкачать

Куда и как запустить модель?

Основу ПО для расчета переходных процессов составляет солвер – программа, решающая систему уравнений. Особую популярность в области переходных процессов имеют солверы, основанные либо на методе узловых потенциалов, либо на методе пространства состояний. Метод пространства состояний подходит для практически любых систем дифференциальных уравнений, а в методе узловых потенциалов используются законы Ома и Кирхгофа, что делает его удобным именно для электрических систем.

Дифференциальные уравнения математических моделей нужно привести к удобоваримому для солвера виду, т. е. к превратить их в систему линейных алгебраических уравнений. Для этого применяется численное интегрирование. Часто используется метод трапеций, его и рассмотрим. Все уравнения ветровой электростанции из предыдущей главы здесь писать не буду, ограничусь одним скромным конденсатором. Ток и напряжение на нем связывает дифференциальное уравнение вида

Применим суть метода трапеций на двух последовательных моментах времени (t-∆t) и (t):

А теперь вынесем величины для момента времени (t-∆t) в отдельное слагаемое:

Тем, кому хочется попробовать свои силы самостоятельно, предлагаю разделаться таким же образом с уравнением для индуктивности.

Величины для момента времени (t-∆t) вынесены в отдельное слагаемое, т. к. известны из расчета предыдущего момента времени. Теперь вместо дифференциального у нас есть обычное линейное алгебраическое уравнение. Если подключить фантазию, то можно заметить, что финальное уравнение очень похоже на резистор, подключенный параллельно с источником тока.

Аналогичным образом уравнения других элементов приводятся к комбинациям резисторов и источников тока. А такие электрические схемы умеет решать каждый уважающий себя солвер, основанный на методе узловых потенциалов.

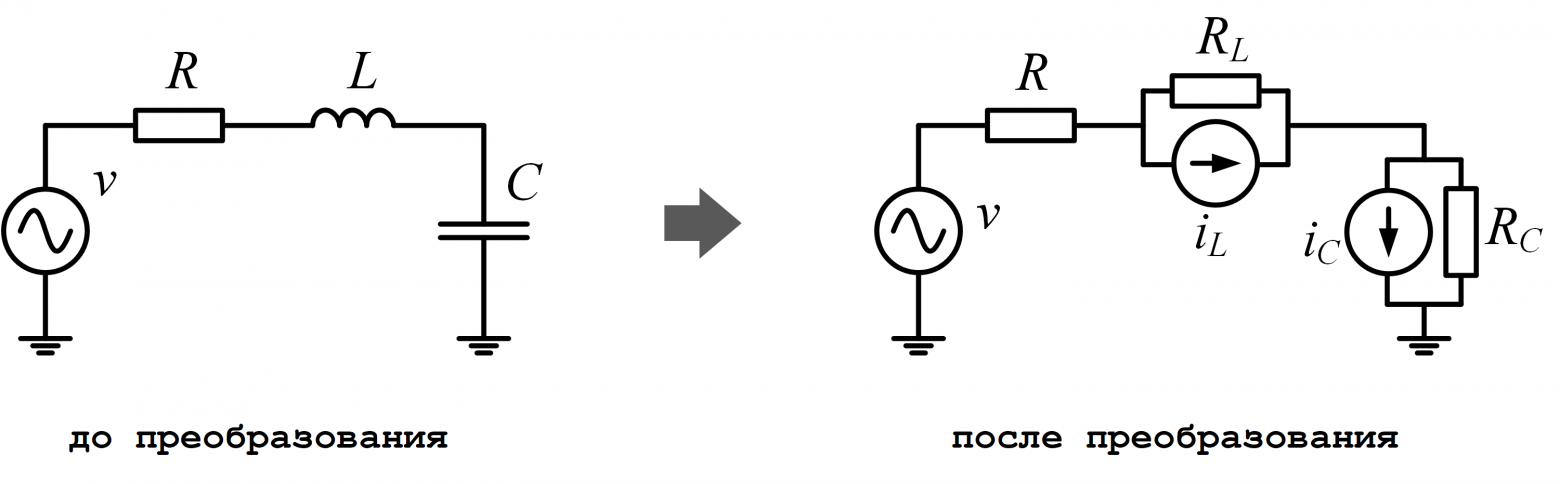
Легким движением руки схема превращается…

Не все элементы в электрических сетях представляются в виде резисторов и источников тока, но все в итоге представляются в виде линейных алгебраических уравнений, которые можно скормить солверу. А если не представляются в виде линейных, то можно линеаризовать, рассчитать якобиан, применить метод Ньютона, но все равно решить, пусть и с итерациями. Но не будем сильно углубляться, об этом тоже как-нибудь в другой раз.

Видео:Пример 7 | Операторный метод расчета цепи 1-го порядка с конденсаторомСкачать

Управление по управлению всеми управлениями

В реальных электрических сетях очень часто используются системы управления: в электроприводе, в ветровых генераторах, в преобразователях постоянного/переменного тока и т. д. Они оказывают сильное влияние на переходные процессы, поэтому их тоже приходится учитывать в расчетах.

Сложность уравнений в системах управления теоретически ограничена лишь фантазией инженеров: дискретные передаточные функции пятого порядка? Пожалуйста. Синус от логарифма? Дайте два, один гиперболический. Из-за этого солвер для систем управления часто приходится использовать отдельный, посложнее.

Впрочем, часто системы управления «однонаправлены», т. е. сигналы приходят с датчиков, проходят обработку и отправляются в управляющие устройства (типа транзисторов) без каких-либо самозацикливаний. Расчет такой системы управления относительно прост, ведь можно последовательно применять всякие алгебраические операции и горя не знать.

Два сложения, два умножения и один интеграл. Легкотня!

Видео:Цепи переменного тока. Комплексные значения сопротивлений, токов и напряжений в цепи. Задача 1Скачать

Все уже сделано до нас

Ну а если не хочется самому разрабатывать модели и солверы, можно воспользоваться уже существующими программными продуктами. Приведу лишь широко известные в узких кругах энергетиков программы, ибо составить исчерпывающий список – задача не из простых. У меня бэкграунд скорее энергетика, чем электронщика, поэтому некоторые популярные программы со схожим функционалом из области электроники наверняка пропустил. Если знаете что-то похожее – поделитесь в комментариях.

EMTP: специализированное ПО для расчета переходных процессов в электрических сетях. Может использоваться и для расчета установившихся процессов
ATP: то же самое
PSCAD: то же самое
PowerFactory: то же самое
Simulink: популярен, знаменит, много методов интегрирования. Но для электрических сетей с большим количеством элементов подходит с трудом. А для прототипирования – очень даже.
SimPowerSystems: надстройка над Simulink’ом специально для электрических систем.
Hypersim: расчеты в реальном времени
RTDS: тоже расчеты в реальном времени
PSS/E: может как и в установившиеся, так и в переходные процессы
LTspice: с упором на электронику

Половина этих продуктов из Канады: EMTP, PSCAD, SimPowerSystems, Hypersim, RTDS. Не скажу, с чем связан такой интерес канадцев к переходным процессам, но разбираются они в них не хуже, чем в хоккее.

Видео:Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Переходный, принужденный и свободный режим в электрической цепи

Давайте рассмотрим некоторые общие вопросы расчета переходных процессов (режимов) на примере включения электрической неразветвленной цепи с емкостью, сопротивлением и индуктивностью (последовательный контур) к источнику напряжений u, которое во времени изменяется по непрерывному произвольному закону, заданному каким-либо аналитическим выражением.

Давайте запишем второй закон Кирхгофа для любого момента времени:

Где i – ток переходного режима, который, как правило, называют переходным током или просто током.

Переходный режим – это состояние электрической цепи, наблюдающееся в течении некоторого (теоретически бесконечно большого) времени после коммутации.

При наступлении принужденного режима электрической цепи уравнение 1 примет вид:

Где: i_пр – ток принужденного режима или просто принужденный ток.

Принужденный режим – это состояние электрической цепи, когда с переходным процессом можно уже не считаться. Принужденный режим, который создается источником произвольного периодически изменяющегося напряжения (или тока), также называют установившийся режим.

Например, изменяющийся по экспоненциальному закону источник напряжения создает принужденный режим, а источник постоянного или изменяющегося по гармоническому закону напряжения, создает установившийся режим. При этом постоянную величину стоит рассматривать как периодическую переменную величину, принимающую в процессе своего изменения одни и те же значения.

Вычитая почленно уравнение 2 из уравнения 1 и обозначая:

Разность напряжений и токов принужденного и переходного режимов называют напряжением или током свободного режима или просто свободным напряжением и током.

Полученные выше уравнения показывают нам, что в свободном режиме, возникающем в цепи при переходе от одного ее состояния к другому, напряжения на всех элементах, создаваемые свободными составляющими токов, взаимно уравновешиваются, но величины свободных напряжений, конечно же, зависят от напряжения источника.

Процесс, происходящий в электрической цепи (согласно уравнению 3), можно рассматривать как бы состоящий из двух накладывающийся друг на друга процессов – свободного, имеющего место исключительно во время переходного режима и принужденного, который как бы наступает сразу. Благодаря свободному процессу и достигается непрерывное приближение к принужденному режиму в переходном режиме. Из чего следует, что в переходном режиме токи и напряжения можно разложить на слагающие свободного и принужденного режимов:

Поскольку принцип наложения может быть применен только к линейным цепям, то приведенное выше разложение допустимо только для линейных цепей. Как вы, наверное, уже догадались, физически существуют только переходные напряжения и токи, а разложения их на свободные и принужденные составляющие является лишь математическим приемом, облегчающим расчет переходных процессов в линейных цепях.

Разложение переходных напряжений и токов соответствует правилу решения неоднородных линейных дифференциальных уравнений, согласно которому общее решение таких уравнений равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения.

Уравнение 4 наглядно показывает, что свободный ток является общим решением однородного дифференциального уравнения и, следовательно, в своем выражении должен содержать постоянные интегрирования, число которых будет равно порядку дифференциального уравнения.

Уравнение 2, в свою очередь, показывает, что принужденный ток представляет собой частное решение неоднородного дифференциального уравнения, а именно то, что получается из общего решения неоднородного дифференциального уравнения при постоянных интегрирования равных нулю. Говоря другими словами, не должно быть в составе принужденного тока слагающих свободного тока. Тогда из первого равенства (формула 6) делаем вывод, что переходный ток i, равный сумме i_св и i_пр, является общим решением того же самого неоднородного дифференциального уравнения.

Начальные значения свободного тока в ветви с индуктивностью i_L_св(0) и свободного напряжения на емкости u_C_св(0) не трудно найти исходя из законов коммутации. Данные манипуляции необходимы для нахождения постоянных интегрирования.

Для удобства расчетов предположим, что электрическая цепь находилась в переходном (произвольном) режиме до коммутации. Ток и напряжения данного режима обозначим i_L_—(t) и u_C_—(t). Напряжение u_C_—(0) и ток i_L_—(0) в момент коммутации (t = 0), а их значения до коммутации будем считать неизвестными.

Поскольку переходное напряжение емкости и переходной ток на индуктивности не могут быть изменены скачкообразно, то на основании уравнения (6) получим:

В случае же когда цепь находилась в принужденном режиме до коммутации, то, обозначив напряжение u_{C пр —} (t) и ток i_{L пр —} (t) для u_{C св —} (0) и i_{L св —} (0) получим:

Если до начала коммутации цепь была отключена и на емкости не было заряда, то есть i_L_пр-(0) = 0 и u_C_пр-(0) = 0:

В простейших цепях переходные процессы, как правило, исследуют классическим методом, который заключается в интегрировании дифференциальных уравнений, которые связывают напряжения и токи электрической цепи в переходном процессе. В результате интегрирования появляются постоянные, значение которых определяют из начальных условий.

Начальными условиями называют значения переходных напряжений и токов на емкостях и индуктивностях, то есть те величины, которые не изменяются скачкообразно в момент коммутации (это следует из законов коммутации).

Так же иногда эти условия могут называть независимые начальные условия. В отличие от них начальные условия всех остальных напряжений и токов называют зависимыми начальными условиями. Зависимые начальные условия определяют из независимых начальных условий и по значениям ЭДС источников питания. Для этого применяются первый и второй законы Кирхгофа.

Важно помнить, что главной трудностью классического метода определения переходных процессов в сложных электрических цепях является вычисление постоянных интегрирования из начальных условий.