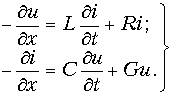Уравнения передачи линии с потерями

Видео:Основы радиочастотной электроники. Лекция 1. Теория длинных линийСкачать

Уравнения передачи линии с потерями

Теория электрических цепей

ГЛАВА 13. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

13.1. Общие положения

До сих пор рассматривались R L С электрические цепи в пред­положении, что параметры сосредоточены в определенных элемен­тах цепи: индуктивность сосредоточена в катушке (энергия маг­нитного поля катушки локализована в ее магнитопроводе), емкость сосредоточена в конденсаторе (энергия электрического поля лока­лизована между обкладками конденсатора); резистивное сопротив­ление сосредоточено в резисторе (преобразование электрической энергии в резисторе в тепловую осуществляется в токопроводящем слое резистора). Такие цепи получили название цепей с сосредо­точенными параметрами

Однако представление электрических цепей в виде цепей с со­средоточенными параметрами не всегда возможно. Например, рас­сматривая передачу электромагнитной энергии в линии связи, фи­дере, антенне, волноводе и т. д., следует учитывать, что магнитное и электрическое поля распределены по всей длине этих устройств и превращение электромагнитной энергии в тепло также происхо­дит по всей длине устройств. В таких цепях приходится сталки­ваться с распределенными по длине нндуктивностями, емкостями, резистивными сопротивлениями, поэтому они называются цепями с распределенными параметрами

Ток и напряжение на выходе сколь угодно малого участка (от­резка) цепи с распределенными параметрами не равны соответ­ственно току и напряжению на его входе и отличаются как по величине, так и по фазе. Таким образом, ток и напряжение в лю­бой точке цепи являются функциями не только времени t, но и пространственных координат (например, расстояния от одного из концов цепи).

Заметим, что деление цепей на два класса – с сосредоточенными и распреде­ленными параметрами, достаточно условно. Одну и ту же цепь следует рассмат­ривать как систему с сосредоточенными или распределенными параметрами в за­висимости от частоты, на которой она работает. Действительно, если на входе цепи действует гармонический сигнал, то в силу конечной скорости распростране­ния электромагнитных колебаний (близкой к скорости света) возмущение от ис­точника за время, равное периоду колебания T, пройдет расстояние, равное дли­не волны электромагнитного колебания: l = cT= c/f, где с – скорость света; f – частота колебания.

При длине цепи, совпадающей с длиной волны колебания, изменение мгновен­ного значения напряжения в конце цепи запаздывает на целый период по срав­нению с изменением мгновенного значения напряжения источника. В цепях, дли­на которых l > l, запаздывание может составлять большое число периодов. Сле­довательно, если длина цепи соизмерима или значительно превышает длину вол­ны распространяющегося в ней электромагнитного колебания, то напряжение (ток) является функцией времени и расстояния от начала цепи. Цепь является системой с распределенными параметрами.

Если длина цепи намного меньше длины волны, то изменения напряжения в любой точке и в конце цепи происходят одновременно с изменением мгновенного значения напряжения источника. Никакого запаздывания в такой цепи нет: напряжение (ток) является только функцией времени. Эту цепь можно считать си­стемой с сосредоточенными параметрами. Например, отрезок коаксиального кабе­ля длиной 30 см при передаче по нему телевизионных сигналов (с наивысшей частотой 8,5 мГц) может считаться цепью с сосредоточенными параметрами, по­скольку l = c/fmax = 3×108/(8,5×106) = 35 м >> 0,3 м. Наоборот, в области дециметро­вых волн (l — десятки сантиметров) этот же отрезок кабеля должен рассматри­ваться как цепь с распределенными параметрами. Отрезок же коаксиального ка­беля длиной, например, в 1 км является цепью с распределенными параметрами и для телевизионного сигнала.

В дальнейшем из обширного класса цепей с распределенными параметрами будем изучать так называемые длинные линии, пред­назначенные для передачи электромагнитной энергии на расстоя­ние и имеющие длину, превышающую длину волны электромагнит­ных колебаний. К ним относятся двухпроводные воздушные линии связи, симметричные и коаксиальные кабельные линии проводных систем связи, фидеры, связывающие радиопередатчики с антеннами и т. д. При этом будем полагать, что конструктивные данные длин­ной линии (материал и диаметр ее проводов, их взаимное распо­ложение) и ее параметры сохраняются неизменными по длине линии. Такие длинные линии называются однородными

Целью изучения однородных длинных линий является анализ распределений напряжений и токов вдоль линии. В основе анализа лежит представление о длинной линии как о цепи с бесконечно большим числом бесконечно малых по величине пассивных элемен­тов, распределенных равномерно по ее длине.

13.2. Уравнения передачи однородной линии

Первичные параметры. Длинные линии могут иметь самую различную конструкцию. Так, двухпроводная воздушная линия (рис. 13.1, а) состоит из параллельных неизолированных проводов, укрепленных с помощью изоляторов на специальных опорах. Сим­метричная кабельная цепь представляет собой два изолированных скрученных друг с другом провода, образующих так называемую пару (рис. 13.1, б). Скрученные между собой пары (или четверки), заключенные в металлическую или пластмассовую защитную обо­лочку, образуют симметричный кабель.

Коаксиальная пара является основой коаксиального кабеля и состоит из внутреннего цилиндра – провода сплошного сечения, помещенного в полый цилиндр (рис. 13.1, в).

Сопротивление R – это сопротивление проводов линии единич­ной длины. Например, для двухпроводной линии сопротивление (Ом/км) где r – удельное сопротивление материала проводов при темпера­туре 20° С, Ом×мм2/м; l – длина линии, м; S – площадь попереч­ного сечения провода, мм2; r – радиус провода, мм.

При температурах, отличных от 20° С, сопротивление проводов вычисляется по формуле где sT – температурный коэффициент, 1/град; Т – температура, ° С. Так, сопротивление двухпроводной медной линии длиной 1 км (километрическое сопротивление) из проводов диаметром 4 мм при температуре Т= 20° С для частоты f = 0 составляет 2,84 Ом/км.

Наличие поверхностного эффекта (вытеснение тока из внутрен­них слоев проводника на его поверхность при увеличении частоты) приводит к увеличению сопротивления R с ростом частоты (см. § 1.2).

Индуктивность L определяется отношением магнитного потока, сцепляющегося с контуром единичной длины, к току, вызываю­щему этот поток. Индуктивность линии складывается из внешней и внутренней индуктивностей. Первая определяется геометриче­скими размерами линии и не зависит от частоты; вторая зависит от материала проводов, их диаметра и частоты.

Поверхностный эффект уменьшает внутреннюю индуктивность при возрастании частоты. Например, километрическая индуктив­ность двухпроводной медной цепи (Гн/км) с диаметром проводов 2r = 4 мм и расстоянием между прово­дами lпр = 200 мм составляет на частоте f = 10 кГц (с учетом маг­нитной проводимости m = 1 и коэффициента действия поверхност­ного эффекта kпэ = 1,8) 1,89 мГн/км.

Емкость С определяется отношением заряда, приходящегося на единицу длины линии, к напряжению между проводами линии.

Для двухпроводной линии емкость (Ф/км) где e – диэлектрическая проницаемость вещества в пространстве между проводами. Например, километрическая емкость воздушной двух­­проводной медной цепи (для воздуха e= 1) из проводов диамет­ром 2r = 4 мм и расстоянием между проводами lпр= 200мм состав­ляет 7,4 нФ/км.

Проводимость G обусловлена несовершенством изоляции и представляет собой активную составляющую проводимости изоля­ции между проводами, отнесенную к единице длины линии. Для воздушной линии проводимость изоляции зависит от климатиче­ских условий (влажности, температуры и др.), чистоты поверхно­стей изоляторов и т. д.

Проводимость изоляции возрастает с ростом частоты (особен­но для кабельных цепей) за счет увеличения потерь в диэлектрике. Для воздушных цепей проводимость (См/км) G = G0 +kпf, где G0 – проводимость изоляции на постоянном токе; kп – коэффициент, учитывающий потери в диэлектрике при переменном токе; f –ча­стота.

Для кабельных цепей G =G0 +wCtgd, где tgd – тангенс угла диэлектрических потерь

После введения первичных параметров можно уточнить поня­тие однородной длинной линии. Однородной называется такая ли­ния, первичные параметры которой неизменны на всей ее длине.

Уравнения передачи однородной линии. Найдем распределения напряжения и тока в линии по ее длине и во времени.

Выделим элементарный участок линии длиной Dx, находящийся на расстоянии х от начала линии (рис. 13.2). Его эквивалентную схему можно приближенно представить в виде последовательно включенных сопротивления RDx и индуктивности LDx и парал­лельно включенных активной проводимости GDx и емкости СDх

Таким образом, линия рассматривается как цепь с бесконечно большим числом звеньев, электрические параметры которых беско­нечно малы. При стремлении Dх к нулю точность такого представ­ления возрастает.

Здесь и далее используются частные производные, так как на­пряжение и ток являются функциями переменных t и х

Уменьшение тока на участке Dх происходит за счет ответвле­ния тока через емкость СDх и проводимость изоляции GDx. Пренебрегая изменением напряжения как величиной второго порядка малости, можно написать (13.1 б)

Разделив обе части уравнений (13.1 а и б) на Dх и перейдя к пределу при Dх ® 0, получим дифференциальные уравнения линии:

Эти уравнения называются телеграфными так как впервые были получены для линии телеграфной связи.

Будем считать, что в линии имеет место режим установившихся гармонических колебаний. Поскольку закон изменения напряже­ний и токов во времени известен, то из дифференциальных урав­нений (13.2) остается найти лишь законы изменения амплитуд и фаз напряжений и токов с расстоянием х

Используя символический метод анализа гармонических коле­баний, в котором

преобразуем уравнения (13.2) к виду

Так как комплексные действующие значения U и I являются функциями только х, уравнения записываются не в частных, а в полных производных.

Продифференцировав первое уравнение из (13.3) по х и под­ставив в него второе уравнение,получим

Введя обозначение перепишем это уравнение в виде

Корни характеристического уравнения p2– 2 =0 равны p1,2 = = ± . поэтому общее решение дифференциального уравнения (13.5) для напряжения в точке х ищем в виде

Из первого уравнения системы (13.3) имеем (13.6 б)

Введя еще одно обозначение запишем решение для тока в точке х в форме (13.7 б)

Постоянные интегрирования A1 и A2 можно найти из начальных условий: при х = 0 Ux = U1 и Ix = I1, где U1 и I1 – напряжение и ток в начале линии. Тогда из (13.6 а и б) для х = 0:

Откуда

Подстановка полученных значений постоянных интегрирования в (13.6) дает следующие уравнения для определения напряже­ния Ux и тока Ix в произвольной точке х длинной линии

Это есть уравнения передачи однородной длинной линии* Параметры и Zв получили название коэффициента распростра­нения и волнового сопротивления линии. Их физический смысл бу­дет рассмотрен позже.

Если учесть, что

то уравнения передачи (13.8) можно переписать в более компакт­ной форме:

В конце линии x = l и Ux = U2 Ix = I2. Уравнения (13.9 а) примут вид (13.9 б)

Разрешая эту систему уравнений относительно напряжения U1 и тока I1 в начале линии, получаем (13.9 в)

Эти уравнения совпадают с известными нам уравнениями пе­редачи (12.35) для симметричного четырехполюсника при l = Гс и Zв = Zс, что вполне понятно, так как линия связи представляет собой симметричный четырехполюсник.

13.3. Падающие и отраженные волны

Обозначим в уравнениях передачи (13.8) Uп = (U1 + I1Zв)/2 и U0 = (U1 – I1Zв)/2. С учетом этих обозначений запись уравнений передачи однородной длинной линии упростится и будет иметь вид где

Напряжение и ток состоят из сумм двух слагаемых. Первые слагаемые уменьшаются с увеличением расстояния от начала ли­нии х, вторые – возрастают. Создается впечатление о существова­нии в линии двух типов волн: падающей и отраженной. Чтобы убе­диться в этом, рассмотрим мгновенные значения напряжения и тока.

Помня, что в (13.10) все величины в общем случае комплексные можно по известным правилам (см. § 3.2) перейти от (13.10) для комплексных значений к уравнениям передачи для мгновенных значений напряжений и токов. Для простоты положим jп = j0 = 0. Тогда

Проанализируем сначала первые слагаемые этих уравнений, которые обозначим

В каждом сечении линии (т. е. в каждой точке х) колебания напряжения и тока являются гармоническими. Амплитуда этих колебаний уменьшается по мере удаления от начала линии по за­кону е–aх. В каждой последующей точке линии колебания отстают по фазе от колебаний в предыдущей точке (на это указывает знак «минус» перед bх).

Если в момент времени t1 сделать фотографию распределения, например, напряжения uxпад вдоль линии, то она будет иметь вид кривой 1 (рис. 13.3). В следующий момент t2 фаза напряжения в каждой точке линии изменится на величину w(t2 – t1), и вся кар­тина как бы сместится вдоль оси х вправо (кривая 2 на рис. 13.3). Аналогичная ситуация будет наблюдаться и в момент времени t3 > t2 (кривая 3 на рис. 13.3).

Если сделать последовательно ряд мгновенных фотографий и затем их проецировать на экран, то создается впечатление движу­щейся волны напряжения вдоль цепи. Фактически же вдоль цепи распространяется состояние равной фазы. Например, можно взять точку цепи х1, соответствующую максимуму напряжения в момент времени t1 (точка А на рис. 13.3) и определить скорость ее пере­мещения. Скорость распространения вдоль цепи состояния равной фазы называется фазовой скоростью распространения

В момент времени t1 в точке х1 имеется определенное фазовое состояние wt1 – bх1. Это же фазовое состояние будет наблюдаться в точке х2, но уже в момент времени t2 wt2 – bх2. Приравнивая их получаем wt1– bх1= wt2– bх2

Фазовую скорость распространения (км/с) найдем как отно­ше­ние расстояния х2– х1, пройденного точкой A, ко времени t2 – t1

Таким образом, уравнения (13.12) описывают волны напряже­ния и тока, распространяющиеся от начала к концу линии. Такие волны называются падающими

Обратимся ко вторым слагаемым выражений (13.11), которые обозначим

Эти слагаемые описывают волны точно такого же характера, как и падающие, но распространяющиеся в обратном направлении, т. е. от конца линии к началу. Эти волны называются отражен­ными волнами напряжения и тока. Амплитуды отраженных волн убывают от конца линии к началу, наибольшая амплитуда наблю­дается в конце линии.

В соответствии с рассмотренной картиной можно сказать, что в установившемся режиме гармонических колебаний напряжение и ток в любой точке линии складываются из падающих и отражен­ных волн напряжения и тока, т. е. ux = uxпад + uxотр; ix = ixпад + + ixотр. Отраженные волны возникают в конце линии.

Складывая эти равенства и вычитая из первого второе, имеем:

Отношение комплексной амплитуды отраженной волны к ком­плексной амплитуде падающей волны называется коэффициентом отражения по напряжению Отсюда

Коэффициент отражения по напряжению показывает, какую часть амплитуды падающей волны в конце линии составляет ампли­туда отраженной волны. Амплитуда отраженной волны тока

В то же время I2отр = siI2пад, где si – коэффициент отражения по току. Отсюда видно, что si = —su, т. е. коэффициент отражения по току равен по значению и противоположен по знаку коэффициенту отражения по напряжению.

Рассмотрим некоторые частные режимы работы линии. Если линия замкнута накоротко на конце (короткое замыкание (КЗ)), т. е. Zн = 0, то коэффициент su= —1, а коэффициент si= 1. Падаю­щая и отраженная волны напряжения в конце линии имеют рав­ные амплитуды и сдвинуты по отношению друг к другу на 180°. Амплитуда результирующей волны напряжения в конце линии бу­дет равна нулю. В то же время падающая и отраженная волны тока будут иметь равные амплитуды, что приведет к увеличению тока в конце короткозамкнутой линии.

При холостом ходе (XX) в конце линии Zн = ¥ коэффициент su = 1 и si=—1, т. е. картина изменится на противоположную: ток в нагрузке будет равен нулю, а напряжение увеличится вдвое. Случай, когда Zн = Zв, рассмотрен ниже.

13.4. Вторичные параметры однородной линии

Волновое сопротивление. Одним из вторичных параметров одно­родной линии является волновое сопротивление линии, определяе­мое через первичные параметры формулой (13.7)

При w= 0 и jв = 0, т. е. волновое сопротивление чисто активное. Точно такой же характер имеет Zв при w=бесконечность;

Для всех реально существующих цепей R/G > L/C, поэтому мо­дуль волнового сопротивления с увеличением частоты уменьшается, стремясь к величине Угол jв изменяется от нулевого значе­ния при w = 0 до нулевого значения при w=бесконечность;. Следовательно, на какой-то частоте он будет иметь максимум. Можно показать, что угол jв на всех частотах является отрицательным. На рис. 13.4 по­казаны графики частотных зависимостей модуля и угла волнового сопротивления однородной линии.

Чтобы выяснить физический смысл волнового сопротивления, воспользуемся выражениями для комплексных амплитуд падаю­щих волн напряжения и тока из (13.10): и откуда

Аналогичным образом можно сказать, что Волновое сопротивление не зависит от длины линии – оно по­стоянно в любой точке линии.

Пример. Определим волновое сопротивление воздушной медной линии из про­водов диаметром 2r = 4 мм и расстоянием между проводами lпр = 20 см и кабель­ной линии с бумажной изоляцией жил диаметром 2r = 0,5 мм на частотах f = 0; 0,8 и 10 кГц для воздушной цепи и f = 0 и 0,8 кГц для кабельной цепи.

Для воздушной линии первичные параметры, взятые из справочника: R = = 2,84 Ом/км; С = 6,3 нФ/км; L = l,93 мГн/км; G = 0,57×10 См/км.

При f = 0 =2,38 кОм. При f = 800 Гц (w= 2p 800рад/с)

На частоте f = 10кГц wL R и wC G, поэтому = 548 Ом.

Для кабельной линии: R = 190 Ом/км, С = 50 нФ/км, L = 0,7 мГн/км, G = 5×10–4 мкСм/км. На частоте f = 0 = 615 кОм. Для частоты f = 800 Гц справедливо соотношение R wL и wC G. Следовательно, Ом.

Согласованное включение линии. Рассмотрим режим работы линии, когда Zн = Zв. В этом случае коэффициенты отражения su = si = 0 и отраженные волны напряжения и тока будут отсут­ствовать (Uxотр = 0 и Ixотр = 0).

Напряжение и ток в любой точке линии, в том числе и на входе (x = 0), будут определяться только падающими волнами. Со­гласно (13.14) , т. е. входное сопротивление такой линии равно ее волновому сопротивлению. Таким об­разом, волновое сопротивление линии является аналогом характе­ристического сопротивления симметричного четырехполюсника

Указанный режим работы линии является режимом согласо­ванного включения. При этом вся энергия поглощается в конце линии нагрузочным сопротивлением. Этот режим работы наиболее выгоден для передачи сигналов связи, так как отражение энергии от нагрузки приводит помимо увеличения рабочего ослабления линии к появлению так называемых эхо-сигналов, накладываю­щихся на основной сигнал и искажающих его.

Уравнения передачи однородной линии в режиме согласован­ного включения могут быть легко получены из (13.9 б и в), если учесть, что при согласованном включении а так­же что

Для любой точки линии (13.15 б)

Коэффициент распространения. Ко вторичным параметрам ли­нии относится также коэффициент распространения, введенный в рассмотрение формулой (13.4):

В режиме согласованного включения линии из (13.15) имеем: или

Отсюда

Для отрезка линии единичной длины (1 км, 1 м и т. д.) можно записать:

Вещественная часть коэффициента распространения a характе­ризует изменение напряжения и тока по абсолютной величине при распространении энергии на расстояние, равное единице длины линии. Она называется коэффициентом ослабления линии и изме­ряется в неперах, отнесенных к единице длины линии (в проводной связи – Нп/км, в радиосвязи – Нп/м). При использовании деся­тичного логарифма вместо натурального

измеряется в дБ/км или дБ/м.

Мнимая часть коэффициента распространения b характери­зуется изменением напряжения и тока по фазе. Она называется коэффициентом фазы линии и измеряется в рад/км или рад/м. Вместо радиан могут использоваться градусы.

Процесс изменения напряжения (тока) вдоль согласованно на­груженной линии можно проиллюстрировать векторной диаграм­мой, показанной на рис. 13.5, а или так называемой спиральной диаграммой, приведенной на рис. 13.5, б

Численные значения коэффициентов a и b можно найти по первичным пара­метрам из общей формулы (13.4). Однако в ряде случаев можно получить бо­лее простые выражения. Так, на высоких частотах (для электрической цепи из меди, например, это частоты 10 кГц), где выполняются условия wL > R и wC > G пользуются упрощенными формулами:

Вывод этих формул дан в специальной литературе и здесь не приводится. Для кабельных цепей в области низких частот (например, от 0 до 800 Гц) вы­полняются соотношения R wL и wC G. В этом случае можно показать, что a = b = . Вторичные параметры a и b зависят от частоты сложным образом. На рис. 13.6, а и б даны графики, качественно отражающие эту зависимость.

Пример. Определим коэффициент распространения воздушной медной линии c параметрами 2r = 4 мм и lпр = 20 см на частоте f = 800 Гц.

Значение коэффициента найдем по полной формуле (13.4), взяв первичные параметры из предыдущего примера:

Отсюда коэффициент ослабления a = 2,86×10–3 Нп/км = 2,86 мНп/км. Перевод непер в децибелы дает a (дБ) = a (Нп)´8,7 = 24,9×10–3 дБ/км. Коэффициент фа­зы b = 17,6×10–3 рад/км.

Постоянная передачи длинной линии. При распространении энергии по линии на расстояние l напряжение и ток уменьшаются в e^(al) раз, а фазы напряжения и тока изменятся на величину bl

Величина al описывает ослабление напряжения и тока при распространении энергии по всей длине линии и называется характеристической (собственной) по­стоянной ослабления линии: Ас = al

Из формул (13.15 а) следует, что

где S1 и S2 – полные мощности на входе и выходе линии. Поэтому

Величина Bс = al = ju1 – ju2 = ji1 – ji2 называется характеристической (собст­венной) постоянной фазы линии

По аналогии с теорией четырехполюсников величина Гс = Ас + jВс является характеристической (собственной) постоянной передачи линии

Заметим, что при отсутствии согласования, т. е. при Zн ¹ Zв условия передачи энергии по линии следует оценивать величиной рабочей постоянной передачи Гp = Аp + jВp по формулам, полученным в общей теории четырехполюсников (см. гл. 12).

13.5. Входное сопротивление линии

Входное сопротивление линии определяется отношением напря­жения и тока в начале линии. Найдем выражение для Zвх, исполь­зуя уравнения передачи линии в форме (13.9 в):

Рассмотрим некоторые частные режимы работы линии.

При согласованном включении линии (Zн = Zв) из (13.16) получим, что Zвх = Zв как и было установлено ранее.

Если выходные зажимы линии замкнуты накоротко (Zн = 0), формула (13.16) упрощается и принимает вид (13.17 а)

В случае разомкнутых выходных зажимов (Zн = бесконечность)

Когда линия нагружена на произвольное сопротивление, не рав­ное волновому (Zн Zв), можно пользоваться для расчетов общей формулой (13.16). Однако иногда удобно выразить Zвх через пара­метры XX и КЗ. Для этого разделим числитель и знаменатель (13.16) на

Данная формула позволяет по измеренным значениям сопротивле­ний XX и КЗ рассчитать входное сопротивление линии.

Существует еще одна форма представления входного сопротивления. Для получения ее перепишем выражение (13.16) после деления на в другом виде:

Обозначим . Тогда

Эта формула дает возможность по заданным параметрам Zв и Zн определить

и затем найти входное сопротивление линии.

Во всех случаях, когда нагрузка на конце линии не равна ее волновому сопротивлению, входное сопротивление определяется гиперболическим тангенсом комплексного аргумента. Чтобы дать представление о характере изменения входного сопротивления ли­нии, на рис. 13.7, а показаны зависимости модулей сопротивле­ний XX и КЗ от длины линии, построенные в соответствии с фор­мулами (13.17), а на рис. 13.7, б изображена зависимость мо­дуля Zвх от частоты из (13.18) при несогласованной нагрузке линии.

13.6. Линия без потерь

Вторичные параметры и уравнения передачи. Реальная линия всегда обладает потерями. Однако в ряде случаев удобно считать линию идеальной, т. е. не имеющей потерь. Линия без потерь – это линия, у которой рассеяние энергии отсутствует, что имеет место при значениях первичных параметров R = 0 и G =0.

Такая идеализация оправдана для коротких по длине линий, работающих на сверхвысоких частотах (фидеров, элементов радио­технических устройств, полосковых линий, измерительных линий, согласующих СВЧ устройств и др.), где выполняются условия R wL и g wC и поэтому резистивными сопротивлением прово­дов и проводимостью изоляции можно пренебречь по сравнению с индуктивным сопротивлением и емкостной проводимостью линии.

Коэффициент распространения линии без потерь

Отсюда коэффициент ослабления a = 0, а коэффициент фазы b = w линейно зависит от частоты.

Волновое сопротивление линии без потерь является чисто активным (резистивным).

Коэффициент фазы b связан с длиной волны электромагнит­ного колебания. Длиной волны l называется расстояние между двумя точками, взятыми в направлении распространения волны, фазы в которых отличаются на 2p. Следовательно, bl = 2p и l = 2p/b

Уравнения передачи линии без потерь получаются из (13.9 в), если учесть, что

При анализе процессов, происходящих в линии без потерь, об­щепринято расположение той или иной точки на линии характе­ризовать ее удалением не от начала линии, как это делали прежде, а от конца линии (рис. 13.8). В этом случае уравнения передачи линии без потерь, выражающие комплексные действующие значе­ния напряжения и тока в произвольной точке линии х, отсчитанной от ее конца, записываются в виде:

Рассмотрим различные режимы работы линии без потерь.

Заменяя комплексные амплитуды их модулями и фазами, т. е. и и полагая для упрощения ju2 = = ji2 = 0, перейдем к уравнениям передачи для мгновенных значе­ний напряжений и токов. Тогда

Эти уравнения описывают падающие волны, распространяю­щиеся в линии слева направо, т. е. от начала к концу линии (рис. 13.9, а). На направление распространения волн указывает знак «плюс» перед bx (напомним, что расстояние х отсчитывается от конца линии).

Таким образом, при согласованном включении линии без по­терь в ней существуют только падающие, или бегущие, волны напряжения и тока. При этом амплитуды колебаний постоянны по всей длине линии (рис. 13.9, б). Данный режим работы линии на­зывают также режимом бегущей волны. Сдвиг фаз между напря­жением их и током ix равен нулю, поэтому энергия бегущей волны носит активный характер.

Короткое замыкание линии. При Zн = 0 напряжение в конце линии U2 = 0. Уравнения передачи (13.19) для данного режима ра­боты линии принимают вид:

Если положить для простоты начальную фазу ji2 тока в конце линии равной нулю, то мгновенные значения напряжения и тока в любой точке линии описываются выражениями:

Амплитуды напряжения и тока явля­ются функциями координаты х. В линии есть точки, в которых амплитуда напряжения (тока) в любой момент времени равна нулю. Это так называемые узлы напряжения (тока). Имеются также точки, в которых амплитуда напряжения (тока) приобре­тает максимальное значение – пучности напряжения (тока).

Узлы напряжения и пучности тока образуются в точках, в ко­торых bx = 0, p, 2p, . так как при этом sin bx = 0 и ux = 0, a cos bx = ±1 и ток ix имеет максимальную амплитуду. Пучности напря­жения и узлы тока возникают в тех точках линии, где

При этих значениях bх sin bх = ±1, в этом случае амплитуда на­пряжения ux оказывается максимальной, a cos bх = 0 и амплитуда тока ix равной нулю. Рассмотрим причины появления узлов и пуч-ностей напряжения и тока.

При КЗ линии коэффициенты отражения имеют значения

т. е. происходит полное отражение энергии, в результате чего в любой точке цепи результирующее напряжение (ток) оказывается равным сумме падающих и отраженных волн. Действительно, из уравнений в комплексной форме (13.20) следует:

Поскольку потерь в линии нет, амплитуды падающих и отражен­ных волн во всех точках линии одинаковы.

Сдвиг фаз между падающей и отраженной волнами напряже­ния в точке х

а между падающей и отраженной волнами тока

Удобно рассматривать в линии без потерь точки х, отстоящие от конца линии на расстояния, кратные четверти длины волны, т. е. кратные l/4. В конце линии (х = 0) ju = —p и ji = 0. Следова­тельно, падающая и отраженная волны напряжения находятся в противофазе, а падающая и отраженная волны тока – в фазе. Поэтому в конце линии наблюдается узел напряжения и пучность тока.

В промежуточных точках между узлами и пучностями фазовые соотношения отличны от 0, p 2p и т. д. В них амплитуды напряжения и тока принимают промежуточные значения между нулем и максимальным значением.

Векторная диаграмма, приведенная на рис. 13.10, иллюстрирует соотношение фаз между падающей и отраженной волнами тока в различных точках КЗ линии.

Распределение модулей комплексных амплитуд напряжения |Ux| и тока |Ix| по длине линии представлено на рис. 13.11. Рас­стояние между соседними узлами (пучностями) равно l/2.

Таким образом, в КЗ линии возникают волны напряжения и тока, которые не распространя­ются вдоль линии, находятся на одном месте. Такие волны называ­ются стоячими а уравнения пере­дачи (13.20) и (13.21) – уравне­ни­ями стоячих волн. Описываемый режим работы линии получил также название режима стоячих волн

Определим входное сопротивление КЗ линии в произвольной точке х. Из (13.20) следует, что

При x = 0, l/2, l, 3l/2, . величина и вход­ное сопротивление = 0. При х = l/4, 3l/4, 5l/4, . вели­чина и входное сопротивление = = ±j¥

На рис. 13.13 приведена зависимость от длины линии (расстояния х от конца линии).

Меняя длину КЗ линии без потерь, можем получить вход­ное сопротивление, имеющее индуктивный характер (в диапазоне x = = 0 . l/4), емкостный характер (х = l/4 . l/2), затем опять индук­тивный (х = l/2 . 3l/4) и т. д.

При длинах, кратных l/4, входное сопротивление короткозамкнутой линии без потерь эквивалентно входному сопротивлению параллельного колебательного контура, а при длинах, кратных l/2 – входному сопротивлению последовательного колебательного контура.

Учитывая, что в линиях, без потерь и, следовательно, частота w и длина линии l (или расстояние от конца линии х) вхо­дят в выражение симметричным образом, приходим к вы­воду, что частотная зависимость аналогична зависимости от длины линии (рис. 13.14). На тех частотах, где bl кратно p/2, , а где bl кратно p, = 0. При фиксированной длине КЗ линия представляет собой двухполюсник с бесконечным числом резонансов.

Размыкание линии. В режиме XX Zн = ¥ и I2 = 0. Уравнения пе­редачи получим из (13.19):

Для мгновенных значений имеем (при начальной фазе напря­жения ju2 = 0):

Сравнивая уравнения передачи (13.22) и (13.23) с уравнениями КЗ линии (13.20) и (13.21), видим, что полученные уравнения так­же являются уравнениями стоячих волн. Разница состоит в том, что узлы и пучности напряжения при XX совпадают с узлами и пучностями тока при коротком замыкании, а узлы и пучности тока разомкнутой линии – с узлами и пучностями напряжения КЗ ли­нии. В конце разомкнутой линии образуется пучность напряжения и узел тока.

Данный режим работы линии по аналогии с предыдущим назы­вается режимом стоячих волн. Входное сопротивление разомкну­той линии без потерь определяется из (13.22):

Его график, отражающий зависимость от х, дан на рис. 13.15.

Включение линии на реактивное сопротивление. Пусть линия нагружена на индуктивность Lн (рис. 13.16, а). При заданной частоте w сопротивление нагруз­ки Zн = jwLн

Из рис. 13.13 видно, что отрезок закороченной линии длиной меньше l/4 име­ет входное сопротивление индуктивного характера. Поэтому всегда можно подо­брать такую длину отрезка l¢, при которой его входное сопротивление равнялось бы заданному сопротивлению Zн. Заменим индуктивность Lн отрезком КЗ линии (рис. 13,16, б). Эта замена позволяет применить теорию КЗ линии и сразу же построить кривые распределения напряжения и тока в линии, нагруженной на ин­дуктивность (рис. 13.16, в). В рассматриваемой линии возникают стоячие волны. Этот режим отличается от режима КЗ замыкания тем, что ближайший узел и пучность сдвинуты от конца линии на некоторое расстояние.

В случае, когда линия нагружена на емкость Cн с сопротивлением Zн = = 1/(jwCн), можно заменить эту емкость отрезком разомкнутой линии длиной l Zв = rв, и рассмотрим распространение по линии волны напря­жения.

Падающая волна не вся поглощается нагрузкой, часть ее отра­жается обратно в линию. Амплитуда отраженной волны меньше амплитуды падающей волны, поэтому падающую волну можно представить в виде суммы двух волн. Одна из них, равная по амплитуде отраженной волне, взаимодействуя с ней, образует стоя­чую волну. Отставшаяся падающая волна является бегущей. Та­ким образом, в линии возникает смешанная волна, состоящая из бегущей и падающей волн. Данный режим работы называется режимом смешанных волн

На рис. 13.17 показано распределение по длине линии модуля комплексной амплитуды напряжения. В линии будут отсутствовать узлы и пучности, а будут наблюдаться минимумы и максимумы амплитуды волн.

Чтобы оценить близость данного режима к режиму бегущей волны, вводят коэффициент бегущей волны

Величина kбв изменяется в пределах от 0 представляет собой амплитуду бегущей волны , т. е. той волны, которая поглощается частью сопротивления нагрузки, рав­ной волновому сопротивлению. Поэтому

Максимальное значение амплитуды смешанной волны

где |Ucв| – максимальная амплитуда стоячей волны. Отсюда на­ходим

Часто используют обратную величину kcв = 1/kбв которую на­зывают коэффициентом стоячей волны

Из общих уравнений передачи линии без потерь (13.19) рассмотрим сначала уравнение для напряжения:

Воспользуемся подстановкой в виде тождества

Тогда после несложных преобразований получим

Уравнение передачи для мгновенных значений напряжения находим как обычно (полагая при этом ju2 = 0):

Первое слагаемое этого уравнения является бегущей волной, второе слагае­мое – стоячей волной. При kбв = 0 первое слагаемое обращается в нуль и в урав­нении присутствует только стоячая волна. При kбв = 1 обращается в нуль второе слагаемое и уравнение содержит только бегущую волну.

Рассматривая аналогичным образом уравнение для тока ix(t), имеем:

Можно сделать некоторые выводы:

если переносимая вдоль линии энергия полностью рассеивается на ее конце (линия нагружена на резистивное сопротивление, рав­ное волновому), то отражение энергии отсутствует и в линии суще­ствуют только бегущие волны;

если энергия в конце линии не рассеивается (короткое замы­кание, холостой ход, реактивная нагрузка), то происходит полное отражение волн, и, как следствие этого, в линии образуются только стоячие волны;

когда переносимая вдоль линии энергия лишь частично рассеи­вается на ее конце (линия замкнута на резистивное сопротивле­ние, не равное волновому), в линии одновременно присутствуют как бегущие, так и стоячие волны.

13.7. Применение отрезков линий с пренебрежимо малыми потерями

Колебательный контур. В технике сверхвысоких частот вместо колебательных контуров на сосредоточенных реактивных элемен­тах используют отрезки короткозамкнутых или разомкнутых линий с малыми потерями. Частотные характеристики входных сопротив­лений таких отрезков (см. рис. 13.14) в области частот, при­легающих к резонансной, достаточно хорошо воспроизводят харак­теристики колебательных контуров. Значения добротностей отрез­ков линий достаточно велики и могут достигать, например, для короткозамкнутых четвертьволновых отрезков нескольких тысяч единиц. Это позволяет успешно использовать их для селекции ко­лебаний весьма высоких частот.

Линейный вольтметр. Непосредственное включение в цепь обыч­ного измерительного прибора при очень высокой частоте на­рушает режим работы цепи, так как вносит в нее добавочное реактивное и резистивное сопротивления. Измерительный прибор с малым входным сопротивлением, включенный через чет­верть­вол­­но­вый отрезок линии, называют линейным вольтметром (рис. 13.19). Подключение измерительного прибора к отрезку ли­нии практически создает КЗ. Входное сопротивление линейного вольтметра оказывается очень большим, и он не оказывает замет­ного влияния на цепь, в которой измеряется напряжение. Измеряе­мое действующее значение напряжения связано с действующим значением тока, протекающего через измерительный прибор, зави­симостью U = rвI, что следует из уравнения (13.20) при х = l/4.

Полосовой фильтр. На сверхвысоких частотах, где потери в ли­нии пренебрежимо малы, КЗ отрезки линии могут быть использо­ваны для построения фильтров. В качестве примера на рис. 13.20, а показана схема полосового фильтра, построенного на двух КЗ от­резках линии. В продольное плечо схемы включен полуволновый отрезок, в поперечное плечо – четвертьволновый. Первый отрезок имеет входное сопротивление, аналогичное входному сопротивлению последовательного колебательного контура. Второй, четверть­волновый, отрезок играет роль параллельного колебательного кон­тура. Эквивалентная электрическая схема фильтра дана на рис. 13.20, б

Четвертьволновой трансформатор сопротивлений. При длине отрезка х = l/4 уравнения передачи (13.19) упрощаются и прини­мают вид:

Такой отрезок можно использовать в качестве согласующего трансформатора сопротивлений. Если включаемые каскадно линии имеют разные волновые сопротивления Zв1 и Zв2, то у четвертьвол­нового согласующего трансформатора в качестве сопротивления нагрузки выступает волновое сопротивление Zв2. Входное сопротивление согласующего трансформатора должно быть равно Zв1. Для выполнения этого условия достаточно выбрать Zв трансформатора равным Тогда

Такой согласующий трансформатор приведен на рис. 13.21.

Пример. На входе отрезка линии без потерь длиной l/2, нагруженного на резистивное сопротивление Rн = 37,5 Ом, включен источник с Uг = 10 В. Волновое сопротивление отрезка Zв = rв = 75 Ом. На расстоянии l/4 от конца отрезка к нему подключен короткозамкнутый шлейф длиной lш = l/8 и волновым сопротивлением Zв = rв = 75 Ом. Определим входное сопротивление отрезка и ток на его входе.

Отрезок линии с короткозамкнутым шлейфом изображен на рис. 13.22. Найдем сначала входное сопротивление части отрезка длиной l/4 от сопротивления Rн до точек а—б, рассматривая эту часть как трансформатор сопротивления: = 150 Ом.

Входное сопротивление КЗ шлейфа длиной l/8, определяется по формуле где

Таким образом, левая часть отрезка длиной l/4 оказалась нагруженной на параллельное соединение сопротивлений и т. е. на сопротивление

Входное сопротивление всего отрезка определим, рассматривая первую поло­вину отрезка как трансформатор сопротивления. Поэтому Ток на входе отрезка линии

Вопросы и задания для самопроверки

1. Привести примеры применения длинных линий.

2. Как рассчитывается длина волны, излучаемой радиовещательной станцией?

3. Рассчитать и построить графики первичных параметров коаксиального кабеля 2,6/9,4 мм в диапазоне частот 812 . 17569 кГц. При расчетах принять e = 1,1; tg d = 0,6×10–4, длина кабеля l = 1 км.

Ответ: L = 2,57×10–4 Гн/км, С = 47,5 нФ/км,

R = 4,1×10–2 Ом/км, G = 1,8×10–14 См/км.

4. Используя данные задачи 3, рассчитать волновое сопротивление кабеля , длину волны l

Ответ: Zв = 73,5 Ом, l = 0,286×109/f

5. Первичные параметры линии на частоте w = 104 с–1 имеют значения: R = 10 Ом/км, L = 0,5 мГн/км, С = 4×10–8 Ф/км, G = = 10–6 См/км. Рассчитать волновое сопротивление, коэффициент распространения и длину волны.

Ответ: Zв = 167,2 Ом, jв = –0,552 рад, a = 0,0157, b = –0,065 (для l = 1 км).

6. Почему кабельные линии связи работают в режиме согласованной нагрузки? Что произойдет, если волновое сопротивление антенного фидера не будет согласовано с входным сопротивлением телевизионного приемника?

7. Запишите уравнения передачи линии без потерь. Чем они отличаются от уравнений передачи линии с потерями?

8. Чем отличаются напряжения и токи в различных сечениях согласованно нагруженной линии без потерь?

9. Укажите различия между следующими понятиями: падающие и отраженные волны; бегущие, стоячие и смешанные волны.

10. Линия без потерь с волновым сопротивлением r = 90 Ом нагружена на сопротивление Rн. Коэффициент бегущей волны равен 0,6. Определить сопротивление нагрузки Rн

11.Какой минимальной длины необходимо взять отрезок линии без потерь с параметрами L = 0,49 мкГн, С = 25 мФ/м, чтобы на частоте f = 108 Гц получить из него индуктивность 0,223 мкГн.

Ответ: короткозамкнутый отрезок длиной 0,347 м.

*При анализе работы длинной линии под U и I в дальнейшем будем пони­мать их комплексные амплитуды (без введения индекса: Um и Im).

Видео:Длинные линии │Цепи с распределенными параметрами │Теория, часть 1Скачать

Длинная линия

Видео:Длинные линии с потерями. Согласование линий.Скачать

Длинная линия

Видео:Лекция 185. Уравнения для длинных линийСкачать

Содержание

1 Дифференциальные уравнения длинной линии
1.1 Погонные параметры 1.2 Эквивалентная схема участка длинной линии 1.3 Телеграфные уравнения 1.4 Условие регулярности линии 1.5 Однородные волновые уравнения длинной линии 1.6 Распределение поля падающей волны

2 Комплексный коэффициент отражения по напряжению 3 Коэффициенты бегущей и стоячей волны 4 Входное сопротивление длинной линии 5 Режимы работы длинной линии

5.1 Режим бегущей волны 5.2 Режим стоячей волны 5.3 Режим смешанных волн

6 Линия без потерь

6.1 Разомкнутая линия 6.2 Замкнутая линия 6.3 Ёмкостная нагрузка 6.4 Индуктивная нагрузка 6.5 Активная нагрузка 6.6 Комплексная нагрузка

7 КПД линии с потерями 8 Пределы применимости теории длинной линии 9 См. также 10 Примечания

Длинная линия — регулярная линия передачи[1], длина которой превышает длину волны (λ) колебаний, распространяющихся в линии.

Характерной особенностью длинных линий является проявление интерференции двух волн, распространяющихся навстречу друг другу. Одна из этих волн создается генератором электромагнитных колебаний, подключенным к линии, и называется падающей. Другая волна может возникать из-за отражения падающей волны от нагрузки, подключенной к противоположному концу линии, и называется отраженной. Отраженная волна распространяется в направлении, обратном падающей волне. Все разнообразие процессов, происходящих в длинной линии, определяется амплитудно-фазовыми соотношениями между падающей и отраженной волнами.

Видео:Длинные линии │Линии без искажений и потерь │Теория, часть 2Скачать

Дифференциальные уравнения длинной линии

Рассмотрим двухпроводную длинную линию, представленную на рисунке 1. На рисунке обозначено: ZН = RН + iXН — комплексное сопротивление нагрузки; z — продольная координата линии, отсчитываемая от места подключения нагрузки.

Погонные параметры

Рис.1 — К выводу дифференциальных уравнений длинной линии

Из электродинамики известно, что линия передачи может быть охарактеризована ее погонными параметрами:

R1 — погонное сопротивление, Ом/м; G1 — погонная проводимость, 1/Ом м; L1 — погонная индуктивность Гн/м; C1 — погонная ёмкость Ф/м;

Погонные сопротивление R1 и проводимость G1 зависят от проводимости материала проводов и качества диэлектрика, окружающего эти провода, соответственно. Чем меньше тепловые потери в металле проводов[2] и в диэлектрике, тем меньше соответственно, R1[3] и G1[4]. Погонные индуктивность L1 и емкость C1 определяются формой и размерами поперечного сечения проводов, а также расстоянием между ними.

Эквивалентная схема участка длинной линии

Рис.2 — Эквивалентная схема участка длинной линии

Выделим из линии элементарный участок бесконечно малой длины dz и рассмотрим его эквивалентную схему, покзанную на рисунке 2. На этой схеме стрелками обозначены направления отсчета напряжения U и тока I в линии; dU и dI — приращения напряжения и тока в линии на элементе длины dz. Значения параметров схемы определяются соотношениями:

Используя эквивалентную схему, запишем выражения для приращений напряжения и тока:

Подставляя сюда значения параметров схемы из (1), получаем:

,

где Z1 = R1 + iωL1, Y1 = G1 + iωC1 — погонные комплексные сопротивление и проводимость линии. Из последних соотношений находим дифференциальные уравнения линии:

Телеграфные уравнения

Основная статья: Телеграфное уравнение

Эти соотношения называются телеграфными уравнениями длинной линии. Они определяют связь между током и напряжением в любом сечении линии. Решим телеграфные уравнения относительно напряжения и тока. Для этого продифференцируем их по z:

При этом учтем, что:

Условие регулярности линии

Данные соотношения являются математическим определением регулярности длинной линии. Смысл соотношения (4) состоит в неизменности вдоль линии ее погонных параметров.

Подставляя в (3) значения производных напряжения и тока из (2), после преобразований получаем:

Однородные волновые уравнения длинной линии

,

где γ — коэффициент распространения волны в линии: .

Соотношения (5) называются однородными волновыми уравнениями длинной линии. Их решения известны и могут быть записаны в виде:

,

где AU, BU и AI, BI — коэффициенты, имеющие единицы измерения напряжения и тока соответственно, смысл которых будет ясен ниже.

Решения волновых уравнений в виде (3.6) имеют весьма характерный вид: первое слагаемое в этих решениях представляет собой падающую волну напряжения или тока, распространяющуюся от генератора к нагрузке, второе слагаемое — отраженную волну, распространяющуюся от нагрузки к генератору. Таким образом, коэффициенты AU, AI представляют собой комплексные амплитуды падающих волн напряжения и тока соответственно, а коэффициенты BU, BI — комплексные амплитуды отраженных волн напряжения и тока соответственно. Так как часть мощности, передаваемой по линии, может поглощаться в нагрузке, то амплитуды отраженных волн не должны превышать амплитуды падающих:

Направление распространения волн в (6) определяется знаком в показателях степени экспонент: плюс — волна распространяется в отрицательном направлении оси z; минус — в положительном направлении оси z (см. рис. 1).Так, например, для падающих волн напряжения и тока можно записать:

,

Коэффициент распространения волны в линии γ в общем случае является комплексной величиной и может быть представлен в виде:

,

где α — коэффициент затухания волны[5] в линии; β — коэффициент фазы[6]. Тогда соотношение (7) можно переписать в виде:

.

Так как при распространении падающей волны на длину волны в линии λЛ фаза волны изменяется на 2π , то коэффициент фазы можно связать с длиной волны λЛ соотношением

.

При этом фазовая скорость волны в линии VФ определяется через коэффициент фазы:

.

Определим коэффициенты A и B , входящие в решения (6) волновых уравнений, через значения напряжения UН и тока IН на нагрузке. Это является оправданным, так как напряжение и ток на нагрузке практически всегда можно измерить с помощью измерительных приборов. Воспользуемся первым из телеграфных уравнений (2) и подставим в него напряжение и ток из (6). Тогда получим:

Сравнив коэффициенты при экспонентах с одинаковыми показателями степеней, получим:

,

где — волновое сопротивление линии[7].

Перепишем (6) с учетом (12):

.

Для определения коэффициентов A и B в этих уравнениях воспользуемся условиями в конце линии z = 0:

.

Тогда из (13) при z = 0 найдем

,

Подставив полученные значения коэффициентов из (14) в (13), после преобразований получим:

.

При выводе (15) учтены определения гиперболических синуса и косинуса[8].

Соотношения для напряжения и тока (15) так же, как и (6), являются решениями однородных волновых уравнений. Их отличие состоит в том, что напряжение и ток в линии в соотношении (6) определены через амплитуды падающей и отраженной волн, а в (15) — через напряжение и ток на нагрузке.

Рассмотрим простейший случай, когда напряжение и ток в линии определяются только падающей волной, а отраженная волна отсутствует[9]. Тогда в (6) следует положить BU = 0, BI = 0:

.

Распределение поля падающей волны

Рис.3. Эпюры напряжений падающей волны в длинной линии. а) амплитуда; б) фаза

На рис.3. представлены эпюры изменения амплитуды |U| и фазы φU апряжения вдоль линии. Эпюры изменения амплитуды и фазы тока имеют такой же вид. Из рассмотрения эпюр следует, что при отсутствии в линии потерь (α[5] = 0) амплитуда напряжения в любом сечении линии остается одной и той же. При наличии потерь в линии (α[5] > 0) часть переносимой мощности преобразуется в тепло (нагревание проводов линии и окружающего их диэлектрика). По этой причине амплитуда напряжения падающей волны экспоненциально убывает в направлении распространения.

Фаза напряжения падающей волны φU = β z изменяется по линейному закону и уменьшается по мере удаления от генератора.

Рассмотрим изменение амплитуды и фазы, например, напряжения при наличии падающей и отраженной волн. Для упрощения положим, что потери в линии отсутствуют, то есть α[5] = 0. Тогда напряжение в линии можно представить в виде:

,

где Γ = BU / AU — комплексный коэффициент отражения по напряжению.

Видео:Урок 261. Потери энергии в ЛЭП. Условие согласования источника тока с нагрузкойСкачать

Комплексный коэффициент отражения по напряжению

Характеризует степень согласования линии передачи с нагрузкой. Модуль коэффициента отражения изменяется в пределах:

| Г | = 0, если отражения от нагрузки отсутствуют и BU = 0[9]; | Г | = 1, если волна полностью отражается от нагрузки, то есть | AU | = | BU | ;

Соотношение (16) представляет собой сумму падающей и отраженной волн.

Рис.4. Векторная диаграмма напряжений в линии с отраженной волной

Отобразим напряжение на комплексной плоскости в виде векторной диаграммы, каждый из векторов которой определяет падающую, отраженную волны и результирующее напряжение (рис. 4). Из диаграммы видно, что существуют такие поперечные сечения линии, в которых падающая и отраженная волны складываются в фазе. Напряжение в этих сечениях достигает максимума, величина которого равна сумме амплитуд падающей и отраженной волн:

.

Кроме того, существуют такие поперечные сечения линии, в которых падающая и отраженная волны складываются в противофазе. При этом напряжение достигает минимума:

.

Если линия нагружена на сопротивление, для которого |Г| = 1 , т. е. амплитуда падающей и отраженной волн равны |BU| = |AU|, то в этом случае Umax = 2|AU|, а Umin = 0.

Рис.5. Эпюры распределения напряжения вдоль линии с отражённой волной. а) Модуль напряжения; б) фаза напряжения.

Напряжение в такой линии изменяется от нуля до удвоенной амплитуды падающей волны. На рис. 5 представлены эпюры изменения амплитуды и фазы напряжения вдоль линии при наличии отраженной волны.

Видео:Длинная линия. Что там внутри?Скачать

Коэффициенты бегущей и стоячей волны

По эпюре напряжения судят о степени согласования линии с нагрузкой. Для этого вводятся понятия коэффициента бегущей волны — kБВ и коэффициента стоячей волны kСВ:

Эти коэффициенты, судя по определению, изменяются в пределах:

,

.

На практике наиболее часто используется понятие коэффициента стоячей волны, так как современные измерительные приборы (панорамные измерители kСВ) на индикаторных устройствах отображают изменение именно этой величины в определенной полосе частот.

Видео:Лекция 193. Сопротивление длинной линии без потерьСкачать

Входное сопротивление длинной линии

Входное сопротивление линии — является важной характеристикой, которое определяется в каждом сечении линии как отношение напряжения к току в этом сечении:

Так как напряжение и ток в линии изменяются от сечения к сечению, то и входное сопротивление линии изменяется относительно ее продольной координаты z. При этом говорят о трансформирующих свойствах линии, а саму линию рассматривают как трансформатор сопротивлений. Подробнее свойство линии трансформировать сопротивления будет рассмотрено ниже.

Видео:Электрические цепи и электротехнические устройства (длинные линии)Скачать

Режимы работы длинной линии

Различают три режима работы линии:

режим бегущей волны; [10] режим стоячей волны; [10] режим смешанных волн.

Режим бегущей волны

Режим бегущей волны характеризуется наличием только падающей волны, распространяющейся от генератора к нагрузке. Отраженная волна отсутствует. Мощность, переносимая падающей волной, полностью выделяется в нагрузке. В этом режиме BU = 0, | Г | = 0, kбв =kсв = 1[10].

Режим стоячей волны

Режим стоячей волны характеризуется тем, что амплитуда отраженной волны равна амплитуде падающей BU = AU т. е. энергия падающей волны полностью отражается от нагрузки и возвращается обратно в генератор. В этом режиме, | Г | = 1, kсв = , kбв = 0[10].

Режим смешанных волн

В режиме смешанных волн амплитуда отраженной волны удовлетворяет условию 0 W Сопротивление нагрузки меньше волнового сопротивления линии RН

Видео:7. Телеграфные уравненияСкачать

Потери в рассогласованной линии

В литературе описаны приблизительные формулы для расчета дополнительных тепловых потерь в несогласованных линиях передачи (кабелях, волноводах) из-за стоячих волн. Ограничение таких формул — собственные потери согласованного кабеля должны быть до 2 дБ. Сегодня всё чаще для СВЧ на частотах выше 1 ГГц используют кабели с высокими потерями. Широкополосные антенны часто имеют КСВ >> 1. Чтобы найти компромисс между длиной линии (например высота подвеса антенны), её стоимостью, оценить потери в заведомо рассогласованной линии (например 75 Ом кабель в системах на 50 Ом) — желательно иметь прикидку потерь в такой линии.

Для оценки потерь в линии с произвольным затуханием и произвольным КСВ — выведем формулу и создадим Excel-калькулятор.

Отраженное напряжение равно (КСВ-1)/(КСВ+1)
Отраженная мощность равна r=((КСВ-1)/(КСВ+1))^2
Коэффициент передачи линии в разах равен d=10^(-loss/10), где loss — паспортное затухание согласованной в линии выраженное в децибелах.

Когда волна доходит до конца линии (например антенны), в антенну уходит d*(1-r).
r отбивается назад и доходит до генератора d*r. Обратно отбивается и доходит до нагрузки d*d*r

После бесконечного количества отражений, коэффициент передачи такой линии (остаток нерассеянной энергии) составит сумму ряда:

Сумма такого ряда имеет решение:

Остаток энергии составит:

p/d это дополнительные потери сверх d связанные именно с наличием стоячих волн в линии

Чтобы всё это мгновенно просчитать для любых d и КСВ, наберем эти формулы в Excel:

Видео:Design of Experiments. Решение задачи согласования линии передачи с нагрузкойСкачать

https://goo.gl/HNCZvE Google Docs

В желтые ячейки подставляем вводные данные, в синих получаем ответ

UPD:
Чтобы понять природу этих повышенных тепловых потерь — продемонстрируем напряженность электрического поля вдоль линии передачи для двух случаев: КСВ=1 (идеально согласованная линия) и КСВ=6 (очень плохо согласованная линия), в одинаковом масштабе Вольт/метр:

Красные пятна максимальной напряженности в рассогласованной линии имеют выше как площадь так и длительность. Эты зоны повышенной напряженности действуют на диэлектрик и вызывают его разогрев, который пропорционален тангенсу угла потерь материала.

🎦 Видео

Лекция 101-1. Линии с распределенными параметрами. Первичные параметры и основные уравненияСкачать

Урок 262. Задачи на потери энергии в ЛЭПСкачать

Лекция 186 Гармонические сигналы в длинных линияхСкачать

Лекция №22 "Передача энергии по линии"Скачать

Как работает ЛЭП. Передача энергии на большие расстояния. Анимационный обучающий ролик. / Урок 3Скачать

Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Длинные линии без потерь.Скачать

Галилео. Эксперимент. Закон БернуллиСкачать

Закон БернуллиСкачать