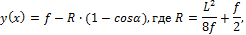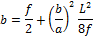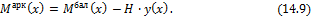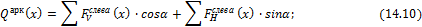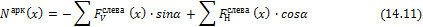Уравнения оси арки при различных очертаниях (6 видео)

Глава 4. Трехшарнирные стержневые системы (арки и рамы).

Элементы трехшарнирных арок, очертание их оси и характеристики оси в сечениях арки.

Трехшарнирной аркой называют стержневую систему, состоящую из двух криволинейных дисков, объединенных между собой ключевым шарниром, и закрепленных на концах шарнирно неподвижными опорами.

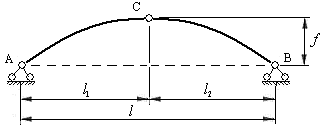
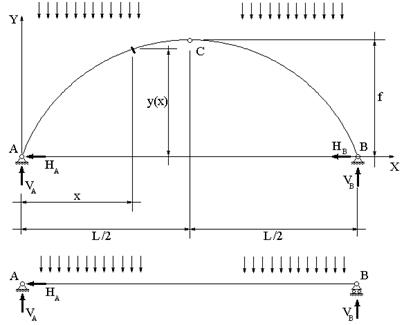
На рис.4.1 показана трехшарнирная арка. Её элементами являются:

— криволинейные диски АС и ВС, которые называют полуарками;

— ключевой шарнир С и опорные (пятовые) шарниры А и В;

— опорная прямая АВ, которая проходит через центры опорных шарниров;

— пролет арки и горизонтальные проекции полуарок и , называемые полупролетами арки;

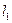
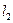
стрела подъема арки 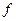, равная расстоянию от ключевого шарнира до опорной прямой.

Опорные шарниры арки, как правило, располагаются в одном уровне, т.е. опорная прямая является горизонтальной прямой. С этой прямой совмещается горизонтальная ось системы координат. Начало системы координат принимается в центре левого опорного шарнира.

Очертание оси арки может быть задано уравнением квадратичной параболы или уравнением окружности. В первом случае арку называют параболической, а во втором – циркульной.

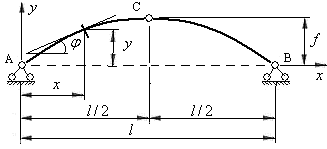
Рассмотрим трехшарнирную арку, отнесенную к системе осей 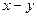(рис.4.2).

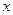
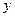
Любое сечение оси арки, взятое на расстоянии от начала координат будет иметь ординату , определяемую из уравнения, принятого для очертания оси арки.

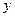
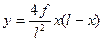
При параболическом очертании арки ордината вычисляется из уравнения:

(4.1)

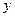
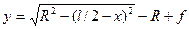
При циркульном очертании арки ордината вычисляется из уравнения:

, (4.2)

где 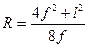(4.3)

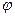
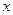
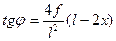
Проведем касательную к оси арки в заданном сечении и обозначим через угол её наклона к горизонтальной оси . Тогда при параболическом очертании оси арки тангенс этого угла будет определяться по формуле:

(4.4)

Синус и косинус того же угла находят по известным формулам тригонометрии:

, (4.5)

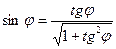
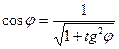
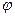
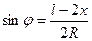
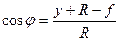
При очертании оси арки по окружности тригонометрические функции угла вычисляются по формулам:

, (4.6)

Опоры трехшарнирных арок могут располагаться в разных уровнях (рис.4.3).

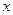
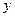
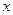
Для таких арок ось совмещается с опорной прямой АВ , а ось направляется перпендикулярно к оси . Характеристики сечений оси арки определяются по приведенным выше формулам, при замене в них длины пролета арки длиной опорной прямой, т.е величиной .

Расчет таких арок сложнее, чем арок с опорами в одном уровне и в данном пособии не приводится.

Видео:Трехшарнирная арка. Определение усилий M,Q,N в обозначенных сечениях аналитическим методомСкачать

Уравнения оси арки при различных очертаниях

14. Расчет трехшарнирных арок

Из прошлого к нам в строительство пришли ряд конструкций, целесообразность которых была проверена Веками Н ашей Цивилизации. Одна из них Распорная система. С учетом работы распорной системы строились Замки, Крепости и Храмы. Так строились и простые дома, в которых проемы и окна – тоже были распорными.

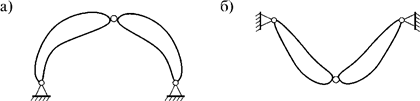
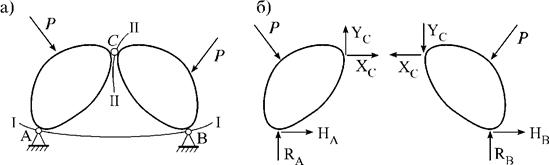
Трехшарнирная система – это система из двух дисков, связанных между собой и основанием тремя шарнирами. Есть трехшарнирные системы двух видов: арочные (рис. 14.1, а) и подвесные системы (рис. 14,1, б).

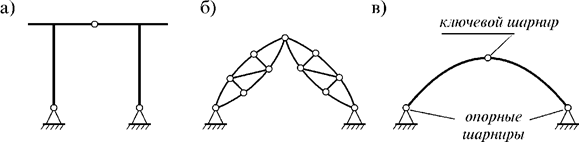
Их расчет мало отличается друг от друга. Поэтому остановимся на арочных системах, которые бывают трех типов: трехшарнирные рамы (рис. 14.2, а), трехшарнирные арочные фермы (рис. 14.2, б) и трехшарнирные арки (рис. 14.2, в).

1. Если в трехшарнирной системе два диска являются прямолинейными или ломанными стержнями, то такая конструкция называется трехшарнирной рамой.

2. Если в трехшарнирной системе два диска являются сквозными решетчатыми конструкциями, то такая система называется трехшарнирной арочной фермой.

3. Арки – сооружения, у которых два диска представляют собой криволинейные стержни, оси которых описаны аналитически или заданы таблично.

Неизменяемая и неподвижная относительно земли трехшарнирная стержневая система статически определима, т. е. ее опорные реакции и внутренние усилия могут быть найдены из уравнений статического равновесия.

W = 3 D–2 Ш– С_оп = 3 ∙ 2 – 2 ∙ 1 – 4 = 0.

Особенность трехшарнирных систем состоит в том, что в них возникает распор (боковое давление) даже от вертикальной нагрузки. Опорные реакции таких систем (рис. 14.3, а) можно определять методом совместных сечений. В результате появляются независимые две части с шестью неизвестными (четыре опорные реакции R_A, R_B, H_A, H_B и две междисковые реакции X_C, Y_C (рис. 14.3, б).

Составив для каждого диска по три уравнения равновесия (всего шесть уравнений), можно определить все эти реакции. Далее каждый диск рассчитывается самостоятельно.

В способах определения опорных реакций и усилий в трехшарнирных арках и рамах принципиального различия нет. Трехшарнирные фермы, после определения их опорных реакций также как и для арок, рассчитывают далее как обычные фермы.

Различные типы трехшарнирных систем нашли широкое применение в мостостроении, сельском строительстве, при перекрытии больших пролетов промышленных цехов, зрелищных сооружений, где они являются экономичными и надежными.

14.1. Общие определения арки

Арка — система криволинейных стержней. К статически определимым системам относятся трехшарнирные арки, имеющие шарнирные опоры на краях и один промежуточный шарнир, чаще всего — центральный (рис.14.4).

Если относительно вертикали, проведенной через шарнир С , трехшарнирная система обладает упругой симметрией, она называется симметричной.

Пролет арки — расстояние между ее опорами L. Опору арки принято также называть пятой арки , центральный шарнир — замком арки, а расстояние f от прямой, соединяющей опорные шарниры до замка арки, — стрелой арки или стрелой подъема арки.

Арки относятся к распорным системам, т.е. таким системам, в опорах которых, в отличие от безраспорных систем, при действии только вертикальной нагрузки возникает ненулевое горизонтальное усилие, называемое распором.

Инженер-строитель может столкнуться с необходимостью выбора между безраспорной системой (балкой) и распорной системой (аркой) для выполнения перекрытия некоторого пролета, например, мостового. При этом арку сопоставляют с соответствующей балкой, т.е. простой балкой на двух опорах, перекрывающей такой же пролет и находящейся под действием такой же вертикальной нагрузки, что и арка.

Ключ арки – место, в котором сечение, перпендикулярное к оси арки, является осью симметрии.

Ось арки – средняя линия, проходящая через центры тяжести сечений арки.

Равномерно распределенная нагрузка на единицу длины – нагрузка постоянной интенсивности, измеряемая на единицу длины оси арки.

Равномерно распределенная нагрузка на единицу проекции – нагрузка постоянной интенсивности, измеряемая на единицу проекции оси арки на какую-либо ось координат .

Продольная сила – направленная по касательной к оси арки проекция главного вектора системы сил, заменяющего в данном поперечном сечении действие отброшенной части арки на ее оставшуюся часть. Положительное направление продольной силы совпадает с направлением нормали к сечению арки и соответствует растяжению.

Поперечная сила – направленная вдоль оси, перпендикулярной к оси арки составляющая главного вектора системы сил, заменяющего в данном поперечном сечении действие отброшенной части арки, на ее оставшуюся часть. Положительное направление поперечной силы совпадает с направлением нормали к сечению, повернутой по часовой стрелке на прямой угол.

Изгибающий момент – в зятый относительно оси поперечного сечения арки момент системы сил, заменяющий в данном поперечном сечении действие отброшенной части арки на ее оставшуюся часть. Положительный изгибающий момент растягивает нижние волокна в арке.

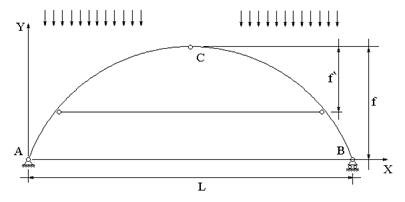
Частным случаем трехшарнирной арки является трехшарнирная арка с затяжкой (рис.14.5).

Затяжка — горизонтальный стержень, предназначенный для полного или частичного восприятия горизонтального распора. Для того , чтобы система при наличии затяжки осталась статически определимой, одну опору арки делают катковой. В этом случае, при отсутствии горизонтальной составляющей нагрузки горизонтальные реакции в опорах будут равными нулю, а затяжка будет воспринимать распор полностью.

При нагрузке определенного вида очертание арки можно задать таким, чтобы в ней не возникало изгибающих моментов. Такие арки называют арками рационального очертания.

14.2. Задание геометрии арки

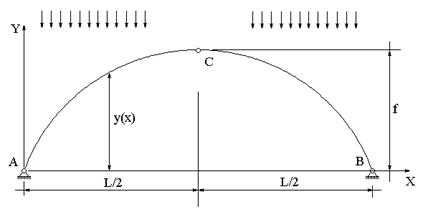
При задании геометрии арки необходимо определить величины пролета L, стрелы f, и функцию y(x), описывающую очертание оси арки (рис.14.4). Для арки с затяжкой, кроме того, необходимо задать высоту над затяжкой f’ (рис.14.5).

Задав значения L и f, мы определяем положение трех точек — опор и замка арки. Если дополнительно потребовать, чтобы ось арки была очерчена по окружности или по параболе, то положение этих трех точек однозначно определит функцию y(x), поскольку через три точки можно провести только одну окружность и только одну параболу.

При круговом очертании арки:

y x = f — R ∙ (1- cosα ), где R = L 2 8 f + f 2 ,

и α = arcsin L 2 R — x R . (14.1)

При параболическом очертании арки:

y x = 4 ∙ f ∙ x ∙ ( L — x ) L 2 ,

α = arctg 4 f L 2 ∙ L — 2 ∙ x . (14.2)

Угол α 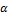в (14.1) и (14.2) — угол наклона касательной к оси арки в данной точке (рис. 14.1). На левой половине арки α >0 , на правой — α . Справедливость формул (14.1) и (14.2) читателю предлагается проверить самостоятельно.

При гиперболическом очертании арки:

y =- b a a 2 + L 2 — x 2 + b + f

b = b a 2 L 2 8 f — f 2

y ‘ = tg α = b a 2 L — 2 x 2( b + f — y ) ,

b a =0,8 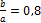– отношение полуосей.

При очертании арки в виде эллипса:

y =- b a a 2 — L 2 — x 2 — b + f

b = f 2 + b a 2 L 2 8 f

y ‘ = tg α = b a 2 L — 2 x 2( y + b — f )

b a =0,8 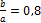– отношение полуосей.

14.3. Статический расчет трехшарнирной арки

В принципиальном отношении расчет трехшарнирной арки не отличается от расчета других статически определимых систем: вначале определяются опорные реакции, затем строятся эпюры изгибающего момента, продольного и перерезывающего усилия, после чего выполняются проверки и, при необходимости, определяются перемещения. Единственная особенность, с которой приходится сталкиваться, — появление чисто вычислительных трудностей, связанных с криволинейностью очертания оси арки.

Как в любой статически определимой системе, реакции в опорах трехшарнирной арки находятся исключительно из статических уравнений (уравнений равновесия). Примем положительные направления реакций в опорах арки в соответствии с рис.14.6.

Из условия равенства нулю суммы проекций всех действующих на систему сил на вертикальную ось имеем:

F V = F V BH — V A — V B =0, (14.3)

где F V BH 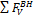— сумма проекций всех действующих на арку внешних сил на вертикальную ось. В (14.3) внешняя сила считается положительной, если она направлена вниз.

Далее, составим уравнение моментов всех действующих на систему сил относительно произвольной точки. Здесь в качестве точки, относительно которой будут вычисляться моменты, выберем точку А. Поскольку линии действия трех опорных реакций из четырех проходят через эту точку, в уравнении останется только одна неизвестная реакция — V_B:

M A = M A BH — V B ∙ L =0, (14.4)

где M A BH 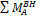— суммарный момент действующих на систему внешних сил относительно точки А. В (14.4) он считается положительным, если направлен по часовой стрелке.

Уравнений (14.3) и (14.4) достаточно, чтобы найти вертикальные реакции в опорах арки. Составив аналогичные уравнения для балки, соответствующей арке (рис. 14.6), легко убедиться, что при отсутствии горизонтальной составляющей нагрузки эти уравнения совпадут с (14.3) и (14.4), а значит вертикальные реакции V_A и V_B в опорах арки и соответствующей ей балки будут одинаковыми.

Из условия равенства суммы проекций всех действующих на систему сил на горизонтальную ось имеем:

F H = F H BH — H A — H B =0, (14.5)

где F H BH 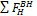— сумма проекций действующих на арку внешних сил на горизонтальную ось. В (14.5) внешняя сила считается положительной, если она направлена вправо.

Четвертое уравнение — условие равенства нулю суммы моментов всех сил, действующих на систему с одной (любой — левой или правой) стороны от промежуточного шарнира относительно этого шарнира. Рассмотрим, например, равновесие левой половины арки:

M C слева = H A ∙ f + V A ∙ L 2 — M C BH слева =0, (14.6)

где M C BH слева 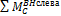— суммарный момент действующих на левую часть арки внешних сил относительно точки С. В (14.6) в качестве его положительного направления принято направление против часовой стрелки.

При отсутствии горизонтальной составляющей внешней нагрузки горизонтальные реакции в опорах арки будут равны и направлены противоположно друг другу, что следует из уравнения (14.5):

— H A = H B = H , (14.7)

Горизонтальное усилие H, возникающее в опорах, называется распором.

Из уравнений (14.3)-(14.6) можно найти четыре неизвестные опорные реакции H_A , H_B , V_A и V_B , после чего приступить к определению изгибающих моментов в сечениях арки.

Рассмотрим сечение, находящееся на произвольном расстоянии x от левой опоры арки (рис. 14.6). Рассматривая равновесие части арки с одной стороны от данного сечения, найдем в нем изгибающий момент. Будем рассматривать часть арки слева от сечения. Тогда

M арк x = V A ∙ x + M BH x + H A ∙ y x , (14.8)

где M BH x 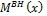— изгибающий момент в рассматриваемом сечении, вызванный исключительно внешними силами, действующими слева от рассматриваемого сечения.

Как мы уже выяснили, при отсутствии горизонтальной составляющей нагрузки вертикальные опорные реакции V_A и V_B в арке и в соответствующей ей балке будут одинаковыми, а горизонтальные реакции в опорах арки равны и противоположно направлены. Изгибающий момент в балке определяется по формуле M бал x = V A ∙ x + M BH x 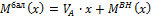. Сопоставляя эту формулу с (14.8), с учетом (14.7) получим:

M арк x = M бал x — H ∙ y x . (14.9)

Величину распора H определяют из дополнительного условия – равенства нулю изгибающего момента в ключевом шарнире C , что приводит к выражению

H = M c бал f ,

где M c бал 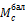– балочный изгибающий момент в сечении C балки от сил, взятых слева или справа от этого сечения; f – стрела арки (рис. 14.6).

Таким образом, при условии отсутствия горизонтальной составляющей нагрузки, зная распор в арке и изгибающий момент в любом сечении балки, соответствующей рассматриваемой арке, момент в этом же сечении арки можно найти и по формуле (14.9).

Для определения продольного и перерезывающего усилий рассмотрим сечение в арке, отстоящее от левой опоры на произвольное расстояние x (рис. 14.6).

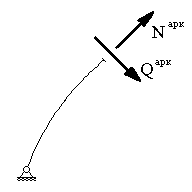
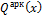
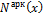
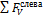
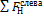
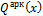
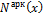
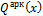
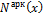
Перерезывающее усилие в арке Q арк x действует перпендикулярно ее оси в данном сечении, а продольное N арк x — вдоль ее оси в данном сечении (рис.14.7). Обозначим сумму проекций всех внешних сил и реакций опор, действующих на рассматриваемую часть сечения, на вертикальную и горизонтальную оси F V слева и F Н слева соответственно. Положительными направлениями этих сил будем считать такие направления, которые будут уравновешиваться положительными Q арк x и N арк x на оси арки (рис.14.8). Составив уравнения равновесия сил, действующих на рассматриваемую часть сечения в осях, совпадающих с направлением действия Q арк x и N арк x (рис.14.9) получим выражения для определения перерезывающего и продольного усилия:

Q арк x = F V слева x ∙ cos α + F Н слева x ∙ sin α ; (14.10)

N арк x =- F V слева x ∙ sinα + F Н слева x ∙ cosα (14.11)

где α – угол наклона касательной к оси арки в сечении К. Особо отметим, что для сечений левой полуарки угол α > 0, s in α > 0, α > 0, а для сечений правой полуарки угол α s in α с os α > 0.

Видео:Арки Виды арок, усилия в арках / строительная механикаСкачать

Цели и задачи курсовых, контрольных работ

Рациональное очертание оси арки

Рациональной осью трёхшарнирной арки заданного пролёта и заданной стрелы подъёма называется такая ось, при которой требуемые условиями прочности поперечные сечения арки будут наименьшими. Очевидно, что наименьшая величина нормального напряжения, согласно выражению (3.11), будет в том случае, когда значение изгибающего момента в сечении будет равно нулю. Последнее же возможно в том случае, когда равнодействующая внутренних проходит через центр тяжести поперечного сечения арки. Этому условию должны удовлетворять все сечения арки.

Рассмотрим типичный случай загружения, когда арка находится под действием равномерно распределённой нагрузки (рис. 3.17).

Исходя из определения рациональной оси арки приравняем к нулю выражение (3.5).

Из этого выражения следует

Рассмотрим частный случай, когда замковый шарнир С расположен в середине пролёта арки. Величина балочного изгибающего момента, как известно, может быть определена из выражения

Распор для симметричного расположения замкового шарнира будет соответственно равен

Подставляя (3.21) и (3.22) в выражение (3.20), получим выражение, описывающее рациональное очертание оси арки, загруженной равномерно распределённой нагрузкой интенсивностью , при расположении замкового шарнира в середине пролёта арок

После арифметических преобразований выражения (3.23) получим выражение, описывающее рациональное очертание оси арки.

Анализ выражения (3.24) свидетельствует о том, что в данном частном случае нагружения трёхшарнирной арки рациональной оказалась ось, описанная по квадратной параболе.

Аналогичным методом можно вывести любую формулу, описывающую рациональное её очертание в зависимости от характера внешнего нагружения. Однако, как показывает опыт, технологически осуществить такие конструкции практически невозможно.

Расчет распорных систем Распорной называется такая система, в результате действия на которую вертикальных внешних нагрузок в ней возникают наклонные опорные реакции.

Расчёт трёхшарнирной арки на статическую нагрузку Как и любой расчёт, расчёт трёхшарнирной арки начинают с определения опорных реакций

Расчёт трёхшарнирной арки на подвижную нагрузку Расчёт на подвижную нагрузку предполагает построение линий влияния всех искомых параметров, определяющих напряжённо-деформированное состояние рассчитываемой конструкции.

Определение напряжений в сечениях арки Нормальные напряжения в поперечных сечениях арки, испытывающих деформацию внецентренного сжатия, определяют по формуле, известной из курса сопротивления материалов