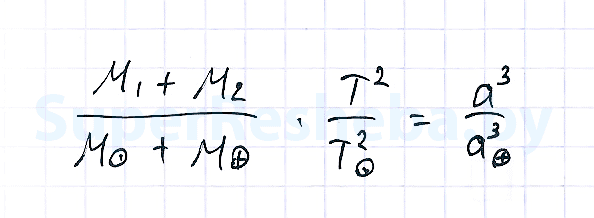Уравнения определения массы звезды 2 уравнения (4 видео)

Уравнения определения массы звезды 2 уравнения

§ 23. М ассы и размеры звёзд

1. Двойные звёзды. Определение массы звёзд

С реди звёзд, которые видны на небе рядом, различают оптические двойные и физические двойные звёзды. В первом случае такие две звезды хотя и видны вблизи, но находятся в пространстве далеко друг от друга. Если же в результате наблюдений выясняется, что они образуют единую систему и обращаются вокруг общего центра масс под действием взаимного тяготения, то они называются физическими двойными звёздами .

Первым, кто доказал, что такие звёзды действительно существуют, был известный английский астроном Вильям Гершель (1738—1822). Множество двойных звёзд открыл и исследовал В. Я. Струве. В настоящее время известно уже более 70 тыс. этих объектов. Когда число звёзд в системе, связанной взаимным тяготением, оказывается более двух, то их называют кратными . В настоящее время считается, что большинство звёзд (более 70%) образуют системы большей или меньшей кратности. В зависимости от того, каким способом можно обнаружить двойственность звезды, их называют по-разному. Если она заметна при непосредственных наблюдениях в телескоп, то это визуально-двойная звезда. Если же об этом можно судить только по спектру, то это спектрально-двойная звезда.

Редким примером двойной звезды, оба компонента которой различимы даже невооружённым глазом, являются Мицар и Алькор в созвездии Большой Медведицы. Среди ярчайших звёзд также были обнаружены двойные: Сириус, Капелла, Кастор и др. Более того, оказалось, что во многих случаях каждая из звёзд такой пары сама состоит из нескольких звёзд. Так, Мицар и Капелла имеют в своём составе четыре компонента, а Кастор — шесть. Выяснилось, что α Центавра является тройной звездой, одна из которых расположена ближе всего к нам и получила название Проксима (в переводе с греческого «ближайшая»).

У двойных звёзд, каждый компонент которых можно наблюдать в отдельности, периоды обращения вокруг общего центра масс обычно бывают от нескольких лет до нескольких сотен или даже тысяч лет. Их орбиты сравнимы по размерам с орбитами планет-гигантов. Большинство спектрально-двойных звёзд имеют периоды обращения порядка нескольких суток, располагаясь друг от друга на расстоянии 5—7 млн км. Самый короткий из известных периодов составляет всего 2,6 ч.

Несмотря на многочисленность двойных звёзд, достаточно надёжно определены орбиты лишь примерно для сотни из них. При известном расстоянии до этих систем использование третьего закона Кеплера позволяет определить их массу. Сравнивая движение спутника звезды с движением Земли вокруг Солнца, можно написать:

= ,

где m 1 и m 2 — массы компонентов звёздной пары; M 1 и M 2 — массы Солнца и Земли; T 1 — период обращения звёзд; T 2 — период обращения Земли; A — большая полуось орбиты двойной звезды; a — большая полуось земной орбиты. Выражая период обращения в двойной системе T в годах (периодах обращения Земли), большую полуось орбиты A в а. е. (расстояниях между Солнцем и Землёй), получаем суммарную массу системы в массах Солнца:

m 1 + m 2 = A 3 : .

Чтобы определить массу каждой звезды, надо изучить движение каждой из них и вычислить их расстояния A 1 и A 2 ( A = A 1 + A 2 ) от общего центра масс. Тогда мы получим второе уравнение:

m 1 : m 2 = A 2 : A 1 .

Решая систему двух уравнений, можно вычислить массу каждой звезды.

У спектрально-двойных звёзд наблюдается смещение (или раздвоение) линий в спектре, которое происходит вследствие эффекта Доплера Напомним, что, согласно этому эффекту, при увеличении расстояния между звездой и наблюдателем длина волны принимаемого излучения увеличивается, поэтому спектральные линии смещаются к красному концу спектра. При уменьшении расстояния длина волны уменьшается, а линии смещаются к фиолетовому концу спектра. . Оно меняется с периодом, равным периоду обращения пары. Если яркости и спектры звёзд, составляющих пару, сходны, то в спектре наблюдается периодическое раздвоение линий (рис. 5.16, а ). Пусть компоненты A и B занимают положения A 2 или B 2 , когда один движется по направлению к наблюдателю, а другой — от него. Спектральные линии приближающейся звезды сместятся к фиолетовому концу спектра, а удаляющейся — к красному. Линии в спектре будут раздвоены. В положениях A 1 и B 1 оба компонента движутся перпендикулярно лучу зрения, и раздвоения линий не наблюдается. Если одна из звёзд настолько слаба, что её линии не видны, то будет наблюдаться периодическое смещение линий более яркой звезды (рис. 5.16, б ).

Рис. 5.16. Раздвоение линий в спектре двойной звезды

Для наблюдателя, который находится в плоскости орбиты спектрально-двойной звезды, её компоненты будут поочерёдно загораживать, «затмевать» друг друга. Такие звёзды называют затменно-двойными или алголями — по названию наиболее известной звезды этого типа β Персея. Её арабское название «эль гуль» (дьявол) постепенно превратилось в Алголь. Возможно, что ещё древние арабы заметили странное поведение этой звезды: в течение 2 суток 11 часов её яркость остаётся постоянной, но затем за 5 часов она ослабевает от 2,3 до 3,5 звёздной величины, а за следующие 5 часов её прежняя яркость восстанавливается (рис. 5.17).

Рис. 5.17. Схема затмений и кривая блеска Алголя

В настоящее время известно более 5 тыс. затменно-двойных звёзд. Их изучение позволяет определить не только характеристики орбиты, но также получить некоторые сведения о самих звёздах. Продолжительность затмения даёт возможность судить о размерах звезды. Рекордсменом здесь является ε Возничего, в системе которой при периоде 27 лет затмение продолжается 2 года. Когда во время затмения свет одной звезды проходит через атмосферу другой, можно детально исследовать строение и состав этой атмосферы. Форма кривой блеска некоторых звёзд свидетельствует о том, что их форма существенно отличается от сферической (рис. 5.18). Близкое расположение компонентов приводит к тому, что газы из атмосферы одной звезды перетекают на другую. Иногда эти процессы принимают катастрофический характер, и наблюдается вспышка новой звезды .

Рис. 5.18. Кривая блеска несферической двойной звезды

Определение масс звёзд на основе исследований двойных звёзд показало, что они заключены в пределах от 0,03 до 60 масс Солнца. При этом большинство из них имеют массу от 0,3 до 3 масс Солнца. Очень большие массы встречаются крайне редко.

Методы изучения спектрально-двойных и затменно-переменных звёзд в настоящее время используются также для поиска планет, обращающихся вокруг других звёзд (экзопланет). К концу 2009 г. было подтверждено открытие около 400 экзопланет, которые составили 340 планетных систем. В их числе было 42 системы, содержавшие не менее двух планет, а одна — не менее 5. Большинство этих планет оказались газовыми гигантами типа Юпитера и Сатурна.

Теперь усилия учёных направлены на поиски планет, которые по своим размерам и массе похожи на Землю и находятся недалеко от звёзд, что обеспечило бы на поверхности планеты условия, необходимые для существования жизни. С этой целью был запущен КА «Кеплер», на котором установлен фотометр, чувствительность которого составляет 10 –5 . Он позволяет заметить ослабление потока света от звезды, вызванное прохождением планет по её диску, всего лишь на одну стотысячную его долю. «Кеплер» исследовал свыше 52 тыс. звёзд в небольшой области неба между созвездиями Лебедя и Лиры. За 2 года работы было найдено более 2300 звёзд, у которых подозревается наличие планет. В 246 случаях это могут быть планеты, которые по размерам сравнимы с Землёй. Ещё не для всех заподозренных случаев получено окончательное подтверждение наличия планет. Однако даже эти предварительные результаты позволяют надеяться, что число экзопланет в нашей Галактике окажется больше, чем считалось ранее. Об этом говорит и открытие 2016 г.: планета с массой всего в 1,3 массы Земли была открыта у ближайшей к Солнцу звезды — Проксимы Центавра.

2. Размеры звёзд. Плотность их вещества

Рис. 5.19. Пятна на диске Бетельгейзе

К сожалению, звёзды расположены так далеко от нас, что за редким исключением они даже в самые мощные телескопы видны как точки. Лишь в последние годы для некоторых самых крупных из них удалось получить изображение в виде диска, на котором обнаруживаются пятна (рис. 5.19).

В большинстве случаев размеры звёзд приходится рассчитывать на основе данных об их светимости и температуре. Светимость звезды рассчитывается по той же формуле, что и светимость Солнца:

L = 4 π R 2 σ T 4 .

Отношение светимостей звезды и Солнца будет равно:

= .

Приняв, что R ☉ = 1 и L ☉ = 1, получаем выражение для вычисления радиуса звезды (в радиусах Солнца):

R = .

Результаты этих вычислений достаточно хорошо согласуются с данными непосредственных измерений с помощью интерферометра размеров наиболее крупных звёзд, расстояния до которых невелики.

Рис. 5.20. Солнце в сравнении с гигантами и сверхгигантами

Рис. 5.21. Размеры звёзд-карликов

Звёзды самой большой светимости (сверхгиганты) действительно оказались очень большими. Красные сверхгиганты Антарес и Бетельгейзе в сотни раз больше Солнца по диаметру (рис. 5.20). Зато диаметр красных карликов, относящихся к главной последовательности, в несколько раз меньше солнечного. Самыми маленькими звёздами являются белые карлики, диаметр которых составляет несколько тысяч километров (рис. 5.21).

Расчёты средней плотности звёзд различных типов, проведённые на основе имеющихся данных об их массе и размерах, показывают, что она может значительно отличаться от средней плотности Солнца. Так, средняя плотность некоторых сверхгигантов составляет всего 10 –3 кг/м 3 , что в 1000 раз меньше плотности воздуха при нормальных условиях. Другой крайностью является плотность белых карликов — около 10 9 кг/м 3 .

В зависимости от массы и размеров звёзды различаются по внутреннему строению, хотя все имеют примерно одинаковый химический состав (95—98% их массы составляют водород и гелий).

Звёзды главной последовательности, температура которых такая же, как у Солнца, или ниже, похожи на него по внутреннему строению. Среди множества звёзд этого типа есть и такие, которые по многим своим характеристикам являются «двойниками» Солнца. Наиболее яркой из них является β Гончих Псов. У более горячих звёзд главной последовательности внешняя конвективная зона отсутствует. В этих звёздах конвекция происходит в ядре протяжённостью до 1 / 4 их радиуса, окружённом лучистой оболочкой (рис. 5.22).

Рис. 5.22. Внутреннее строение звёзд различных классов

Гиганты и сверхгиганты имеют очень маленькое ядро (его радиус около 0,001 доли радиуса звезды). Термоядерные реакции происходят в окружающем его тонком слое; далее на протяжении около 0,1 радиуса звезды происходит передача энергии излучением. Практически весь остальной объём ( 9 / 10 радиуса) составляет протяжённая конвективная зона. Белые карлики состоят из вырожденного газа, давление которого определяется лишь его плотностью и не зависит от температуры. Равновесие такой «экзотической» звезды, масса которой равна солнечной, наступает лишь тогда, когда она сожмётся до размеров, примерно равных размерам Земли. Внутри белого карлика температура достигает 10 млн К и практически не меняется; только в тонкой оболочке из «обычного» вещества она резко падает до 10 000 К.

В 1996 г. были открыты космические тела, которые являются промежуточным звеном между звёздами и планетами. Они получили название «коричневые карлики», поскольку излучают слабо и только в инфракрасном диапазоне. Именно это излучение было обнаружено приборами, установленными на борту искусственных спутников. Коричневые карлики обладают слишком малой массой, что не обеспечивает температуры, необходимой для протекания термоядерной реакции превращения водорода в гелий. Гравитационное сжатие их массы достаточно лишь для того, чтобы достигнутая температура обеспечила в течение короткого (по космическим меркам) времени превращение дейтерия (тяжёлого изотопа водорода) в гелий. Масса коричневых карликов составляет всего лишь 0,01—0,07 массы Солнца. Про них можно сказать, что они ещё не звёзды, но уже не планеты.

Понять, как связаны между собой различные типы звёзд, как они возникают и как происходит их эволюция, оказалось возможным только на основе изучения всей совокупности звёзд, образующих огромные звёздные системы — галактики .

П РимеР РешениЯ задаЧи

1. Период обращения двойной звезды 100 лет. Большая полуось видимой орбиты a = 2,0 ʺ , а параллакс p = 0,05 ʺ . Определите сумму масс и массы звёзд в отдельности, если они отстоят от центра масс на расстояниях, относящихся как 1 : 4.

Так как A 1 : A 2 = m 2 : m 1 , то = и m 1 = 4 m 2 .

По третьему закону Кеплера

m 1 + m 2 = A 3 : T 2 или 4 m 2 + m 2 = A 3 : T 2 ,

т. е. 5 m 2 = A 3 : T 2 .

A = ,

A = = 40 а. е.;

m 2 = = 1,28; m 1 = 4 • 1,28 = 5,12.

Ответ : m 1 = 5,12 массы Солнца, m 2 = 1,28 массы Солнца.

2. Во сколько раз Арктур больше Солнца, если светимость Арктура равна 100, а температура 4500 К?

= • = 10 • = 18.

— ?

Ответ : радиус Арктура больше радиуса Солнца в 18 раз.

В опросы 1. Чем объясняется изменение яркости некоторых двойных звёзд? 2. Во сколько раз отличаются размеры и плотности звёзд-сверхгигантов и карликов? 3. Каковы размеры самых маленьких звёзд?

У пражнение 19 1. Определите сумму масс двойной звезды Капелла, если большая полуось её орбиты равна 0,85 а. е., а период обращения 0,285 года. 2. Во сколько раз светимость Ригеля больше светимости Солнца, если его параллакс равен 0,003 ʺ , а видимая звёздная величина 0,34? 3. Какова средняя плотность красного сверхгиганта, если его диаметр в 300 раз больше солнечного, а масса в 30 раз больше массы Солнца?

Видео:Нейтронные звезды. Массы и радиусы. Часть 2.Скачать

Решебник по астрономии 11 класс на урок №24 (рабочая тетрадь) — Двойные звёзды. Массы звёзд

вкл. 28 Ноябрь 2016 .

Решебник по астрономии 11 класс на урок №24 (рабочая тетрадь) — Двойные звёзды. Массы звёзд

1. Для каждого из определений подберите правильные ответы из общего перечня:

а) визуально-двойные звёзды;
б) спектрально-двойные звёзды;
в) оптические двойные звёзды;
г) физические двойные звёзды;
д) затменно-двойные звёзды.

Две звезды, движущиеся вокруг общего центра масс под действием сил тяготения, — г.

Неразрешимые в телескоп пары звезд, видимая звездная величина которых меняется, так как плоскость их орбит совпадает с лучом зрения наблюдателя, — д.

Двойные звезды, двойственность которых обнаруживается в телескоп, — а.

Две звезды, случайно спроецированные в близкие точки на небесной сфере, — в.

Тесные пары звезд в спектре которых наблюдается периодическое смещение или раздвоение спектральных линий, — б.

2. Закончите предложения.

Примером оптической двойной звезды является Мицар и Алькор.

Разность звездных величин в минимуме и максимуме блеска называется амплитудой блеска.

Промежуток времени между двумя последовательными максимумами или минимумами блеска называется периодом переменности.

Изменение вида кривой блеска затменно-переменной звезды позволяет определить следующие характеристики орбит ее компонентов: период обращения, эксцентриситет орбиты; наклонение плоскости орбиты.

3. Исходя из третьего закона Кеплера, обобщенного Ньютоном, выведите формулу для определения суммы масс компонентов физической двойной звезды.

Сумму масс визуально-двойных звёзд определяют с использованием третьего закона Кеплера в формулировке Ньютона:

4. У двойной звезды годичный параллакс составляет 0,05″, большая полуось видимой орбиты равна 2,0″, а период обращения компонентов 100 лет. Найдите сумму масс звезд, а также массу каждой звезды в отдельности, если звезды отстоят от центра масс на расстояниях, относящихся как 4:1.

5. Закончите предложения.

Изменение линий спектров спектрально-двойных звезд происходит следующим образом:

а) если яркости и спектры звезд, составляющих пару, сходны, то в спектре двойной звезды наблюдается периодическое раздвоение линий;
б) у приближающейся звезды спектральные линии сместятся к фиолетовому концу спектра;
в) у удаляющейся звезды спектральные линии сместятся к красному концу спектра.

6. Каким положениям на кривой видимой яркости затменно-двойной звезды соответствуют взаимные расположения ее компонентов в пространстве (рис. 24.1)?

Видео:Тема 18. Двойные звёзды. Масса звёздСкачать

Лекция на тему: «Массы и размеры звезд».

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Массы и размеры звезд

1. Двойные звезды

Массы звезд. Как мы убедились на примере Солнца, масса звезды является той важнейшей характеристикой, от которой зависят физические условия в ее недрах. Прямое определение массы возможно лишь для двойных звезд.

Двойные звезды называются визуально-двойными, если их двойственность может быть замечена при непосредственных наблюдениях в телескоп.

Примером визуально-двойной звезды, видимой даже невооруженным глазом, является с, Большой Медведицы, вторая звезда с конца «ручки» ее «ковша». При нормальном зрении совсем близко от нее видна вторая слабая звездочка. Ее заметили еще древние арабы и назвали Алькор (Всадник). Яркой звезде они дали название Мицар . Мицар и Алькор отстоят друг от друга на небе на 11′. В бинокль таких звездных пар можно найти немало.

Системы с числом звезд n≥З называются кратными . Так, в бинокль видно, что ε Лиры состоит из двух одинаковых звезд 4-й звездной величины с расстоянием между ними 3′. При наблюдении в телескоп ε Лиры — визуально-четверная звезда. Однако некоторые звезды оказываются лишь оптически-двойными , т. е. близость, таких двух звезд является результатом случайной проекции их на небо. На самом деле в пространстве они далеки друг от друга. Если же при наблюдении звезд выясняется, что они образуют единую систему и обращаются под действием сил взаимного притяжения вокруг общего центра масс, то их называют физическими двойными .

Множество двойных звезд открыл и изучил известный русский ученый В. Я. Струве. Самые короткие из известных периодов обращения визуально-двойных звезд — несколько лет. Изучены пары с периодами обращения в десятки лет, а пары с периодами в сотни лет изучат в будущем. Ближайшая к нам звезда а Центавра является двойной. Период обращения ее составляющих (компонентов) 70 лет. Обе звезды в этой паре по массе и температуре сходны с Солнцем.

Рис. 73 Орбита спутника двойной вокруг главной звезды, расстояние которой от нас составляет 10 пк. (Точки отмечают измеренные положения спутника в указанные годы. Их отклонения от эллипса вызваны погрешностями наблюдений.)

Главная звезда обычно не находится в фокусе видимого эллипса, описываемого спутником, потому что мы видим его орбиту в проекции искаженной (рис. 73). Но знание геометрии позволяет восстановить истинную форму орбиты и измерить ее большую полуось а в секундах дуги. Если известно расстояние D до двойной звезды в парсеках и большая полуось орбиты звезды-спутника в секундах дуги, равная а», то в астрономических единицах она будет равна:

Сравнивая движение спутника звезды с движением Земли вокруг Солнца (для которой период обращения Т =1 год, а большая полуось орбиты а =1 а. е.), мы по III зэкону Кеплера можем написать:

где m ₁ и m ₂ — массы компонентов в паре звезд, М и М — массы Солнца и Земли, а T — период обращения пары в годах. Пренебрегая массой Земли в сравнении с массой Солнца, мы получаем сумму масс звезд, составляющих пару, в массах Солнца:

Чтобы определить массу каждой звезды, надо изучить движение компонентов относительно окружающих звезд и вычислить их расстояния А ₁ и А ₂ от общего центра масс. Тогда получим второе уравнение m ₁ :m ₂ =А ₂ :А ₁ и из системы двух уравнений найдем обе массы отдельно.

Двойные звезды в телескоп нередко представляют собой красивое зрелище: главная звезда желтая или оранжевая, а спутник белый или голубой.

Если компоненты двойной звезды при взаимном обращении подходят близко друг к другу, то даже в самый сильный телескоп их нельзя видеть раздельно. В этом случае двойственность может быть определена по спектру. Такие звезды будут называться спектрально-двойными . Из-за эффекта Доплера линии в спектрах звезд будут смещаться в противоположные стороны (когда одна звезда удаляется от нас, другая приближается). Смещение линий меняется с периодом, равным периоду обращения пары. Если яркости и спектры звезд, составляющих пару, сходны, то в спектре двойной звезды наблюдается периодически повторяющееся раздвоение спектральных линий (рис. 74). Пусть компоненты занимают положения А ₁ и В ₁ или A ₃ и В ₃ , тогда один из них движется к наблюдателю, а другой — от него (рис. 74, I, III). В этом случае наблюдается раздвоение спектральных линий. У приближающейся звезды спектральные линии сместятся к синему концу спектра, а у удаляющейся — к красному. Когда же компоненты двойной звезды занимают положения А ₂ и В ₂ или A ₄ и В ₄ (рис. 74, II, IV), то оба они движутся под прямым углом к лучу зрения и раздвоения спектральных линий не получится.

Рис. 74. Объяснение раздвоения, или колебания, линий в спектрах спектрально-двойных звезд

Если одна из звезд светится слабо, то будут видны линии только другой звезды, смещающиеся периодически.

Компоненты спектрально-двойной звезды могут при взаимном обращении поочередно загораживать друг друга. Такие звезды называются затменно-двойными или алголями, по названию своего типичного представителя β Персея. Во время затмений общая яркость пары, компонентов которой мы по отдельности не видим, будет ослабевать (положения В и D рис. 75.) В остальное же время в промежутках между затмениями она почти постоянна (положения А и С) и тем дольше, чем короче длительность затмений и чем больше радиус орбиты. Если спутник большой, но сам дает мало света, то когда яркая звезда затмевает его, суммарная яркость системы будет уменьшаться лишь ненамного.

Рис. 75. Изменения видимой яркости р Лиры и схема движения ее спутника. (Форма звезд, близко расположенных друг к другу, вследствие их приливного воздействия может сильно отличаться от сферической.)

Древние арабы назвали β Персея Алголем (испорченное эль гуль), что означает «дьявол». Возможно, что они заметили ее странное поведение: в течение 2 дней 11 ч яркость Алголя постоянна, затем за 5 ч она ослабевает от 2,3 до 3,5 звездной величины, а затем за 5 ч яркость ее возвращается к прежнему значению.

Анализ кривой изменения видимой звездной величины в функции времени позволяет установить размеры и яркость звезд, размеры орбиты, ее форму и наклон к лучу зрения, а также массы звезд. Таким образом, затменно-двойные звезды, наблюдаемые также и в качестве спектрально-двойных, являются наиболее хорошо изученными системами. К сожалению, таких систем известно пока сравнительно мало.

Периоды известных спектрально-двойных звезд и алголей в основном короткие — около нескольких суток.

В общей сложности двойственность звезд очень распространенное явление. Статистика показывает, что до 30% всех звезд, вероятно, являются двойными.

Определенные описанными методами массы звезд различаются гораздо меньше, чем их светимости: примерно от 0,1 до 100 масс Солнца. Очень большие массы встречаются крайне редко. Обычно звезды обладают массой меньше пяти масс Солнца.

Именно масса звезд обусловливает их существование и природу как особого типа небесных тел, для которых характерна высокая температура недр (свыше 10 7 К) — Происходящие при такой температуре ядерные реакции превращения водорода в гелий являются у большинства звезд источником излучаемой ими энергии. При меньшей массе температура внутри небесных тел не достигает тех значений, которые необходимы для протекания термоядерных реакций.

Эволюция химического состава вещества во Вселенной происходила и происходит в настоящее время главным образом благодаря звездам. Именно в их недрах идет необратимый процесс синтеза более тяжелых химических элементов из водорода.

Пример решения задачи

Задача. У двойной звезды период обращения 100 лет. Большая полуось видимой орбиты а = 2,0″, а параллакс ρ = 0,05″. Определите сумму масс и массы звезд в отдельности, если звезды отстоят от центра масс на расстояниях, относящихся как 1:4.

1. Определите сумму масс двойной звезды Капеллы, если большая полуось ее орбиты равна 0,85 а. е., а период обращения составляет 0,285 года.

2. Если бы по орбите Земли двигалась звезда с такой же массой, как у Солнца, каков был бы период ее обращения?

3. По рисунку 73 оцените период обращения спутника, большую полуось орбиты и вычислите сумму масс компонентов. Считать, что большая полуось орбиты лежит в плоскости рисунка.

2. Размеры звезд. Плотность их вещества

Покажем на простом примере, как можно сравнить размеры звезд одинаковой температуры, например Солнца и Капеллы (α Возничего). Эти звезды имеют одинаковые спектры, цвет и температуру, но светимость Капеллы в 120 раз превышает светимость Солнца. Так как при одинаковой температуре яркость единицы поверхности звезд тоже одинакова, то, значит, поверхность Капеллы больше, чем поверхность Солнца, в 120 раз, а диаметр и радиус ее больше солнечных в раз.

Определить размеры других звезд позволяет знание законов излучения.

Так, в физике установлено, что полная энергия, излучаемая в единицу времени с 1 м 2 поверхности нагретого тела, равна: i = σТ 4 , где σ — коэффициент пропорциональности, а T — абсолютная температура * . Относительный линейный диаметр звезд, имеющих известную температуру Т, находят из формулы

* ( Закон Стефана — Болыдмана установлен австрийскими физиками Й. Стефаном (экспериментально) и Л. Больцманом. )

где r — радиус звезды, i — излучение единицы поверхности звезды, r , i , T относятся к Солнцу, a L = l. Отсюда

в радиусах Солнца.

Результаты таких вычислений размеров светил полностью подтвердились, когда стало возможным измерять угловые диаметры звезд при помощи особого оптического прибора (звездного интерферометра).

Звезды очень большой светимости называются сверхгигантами. Красные сверхгиганты оказываются такими и по размера (рис. 76). Бетельгейзе и Антарес в сотни раз больше Солнца по диаметру. Более далекая от нас VV Цефея настолько велика, что внутри нее поместилась бы Солнечная система с орбитами планет до орбиты Юпитера включительно! Между тем массы сверхгигантов больше солнечной всего лишь в 30-40 раз. В результате даже средняя плотность красных сверхгигантов в тысячи раз меньше, чем плотность комнатного воздуха.

Рис. 76. Сравнительные размеры Солнца и звезд разных типов (масштабы в двух частях рисунка различны)

При одинаковой светимости размеры звезд тем меньше, чем эти звезды горячее. Самыми малыми среди обычных звезд являются красные карлики. Массы их и радиусы — десятые доли солнечных, а средние плотности в 10-100 раз выше, чем плотность воды. Еще меньше красных белые карлики — но это уже необычные звезды.

У близкого к нам и яркого Сириуса (имеющего радиус примерно вдвое больше солнечного) есть спутник, обращающийся вокруг него с периодом 50 лет. Для этой двойной звезды расстояние, орбита и массы хорошо известны. Обе звезды белые, почти одинаково горячие. Следовательно, поверхности одинаковой площади излучают у этих звезд одинаковое количество энергии, но по светимости спутник в 10 000 раз слабее, чем Сириус. Значит, его радиус меньше в √10000= 100 раз, т. е. он почти такой же, как Земля. Между тем масса у него почти как у Солнца! Следовательно, белый карлик имеет громадную плотность — около 10 9 кг/м 3 . Существование газа такой плотности было объяснено следующим образом: обычно предел плотности ставит размер атомов, являющихся системами, состоящими из ядра и электронной оболочки. При очень высокой температуре в недрах звезд и при полной ионизации атомов их ядра и электроны становятся независимыми друг от друга. При колоссальном давлении вышележащих слоев это «крошево» из частиц может быть сжато гораздо сильнее, чем нейтральный газ. Теоретически допускается возможность существования при некоторых условиях звезд с плотностью, равной плотности атомных ядер.

Мы еще раз видим на примере белых карликов, как астрофизические исследования расширяют представления о строении вещества; пока создать в лаборатории такие условия, какие есть внутри звезд, еще нельзя. Поэтому астрономические наблюдения помогают развитию важнейших физических представлений. Например, для физики громадное значение имеет теория относительности Эйнштейна. Из нее вытекает несколько следствий, которые можно проверить по астрономическим данным. Одно из следствий теории состоит в том, что в очень сильном поле тяготения световые колебания должны замедляться и линии спектра смещаться к красному концу, причем это смещение тем больше, чем сильнее поле тяготения звезды. Красное смещение было обнаружено в спектре спутника Сириуса. Оно вызвано действием сильного поля тяготения на его поверхности. Наблюдения подтвердили это и ряд других следствий теории относительности. Подобные примеры тесной взаимосвязи физики и астрономии характерны для современной науки.

Пример решения задачи

Задача. Во сколько раз Арктур больше Солнца, если светимость Арктура 100, а температура 4500 К?