Давайте сначала вспомним понятие плоской волны. Что это такое? Это вид волны, характерным свойством которой является плоская форма волновой поверхности. Волновая поверхность — это набор точек в среде или пространстве (в случае электромагнитных волн), в которых волна имеет одинаковую фазу колебаний.
Таким образом: при распространении плоской волны в двумерной среде волновые поверхности образуют прямые линии, параллельные друг другу; при распространении в трехмерном пространстве — плоскости (рис. 1).

Здесь мы будем рассматривать второй случай — (электромагнитную) волну, распространяющуюся в трехмерном пространстве.
Как создать такую абстрактную волну? Возможно ли это вообще? Об этом и других вопросах, связанных с электромагнитной плоской гармонической волной, вы прочитаете далее.
Прежде чем мы разберемся с плоской волной, давайте объясним понятие гармонической волны. По-другому ее называют синусоидальной волной. Хорошим примером этого является акустическая волна, источником которой является яркий камертон. График, показанный на рис. 2, показывает изменение давления воздуха в зависимости от положения x для определенного момента времени. Волна распространяется вдоль оси x, т.е. кривая движется во времени вправо со скоростью звука.

Гармоническая волна создается источником, который вибрирует гармонически. Мы уже знаем, что когда речь идет об электромагнитной волне, источником, совершающим гармоничные колебания, являются заряды в LC-контуре. Таким образом, радиоволна — это гармоническая волна. Как и любая гармоническая волна, радиоволна имеет определенную длину и частоту, которые связаны следующим образом: λ = v / f , где где λ — длина волны, v — скорость распространения волны в среде, f — частота волны.
На рис. 3. схематически показана конфигурация электрического поля (синие линии) и магнитного поля (красные линии) вокруг дипольной антенны, расположенной вертикально. Поля демонстрируют осевую симметрию. Волна распространяется приблизительно в радиальном направлении. Поля «идут одинаковым фронтом», они согласованы по фазе. Обратите внимание, что линии электрического и магнитного поля перпендикулярны друг другу в каждой точке пространства.

Вернемся к плоской волне и зададим вопрос: можно ли получить электромагнитную волну такую, что везде на бесконечной плоскости электрическое поле имеет одинаковое значение, направление и отдачу?
Теоретически это возможно. Достаточно представить себе бесконечную пластину (см. рис. 4), в которой электрические заряды гармонично колеблются в вертикальном направлении. Они создают электромагнитные волны по обе стороны пластины, идущие от нее в противоположных направлениях. Их направление перпендикулярно пластине. (Она не может быть другой из-за симметрии системы).

На любой прямой, перпендикулярной плоскости с токами, мы будем иметь электрическое и магнитное поле со структурой, показанной на рис. 5.

Волна распространяется в направлении оси z. Векторы напряженности электрического поля E направлены вдоль оси x, а векторы магнитной индукции B — вдоль оси y.
Обратим внимание на характерную особенность электромагнитной волны, хорошо заметную в структуре плоской волны. А именно, векторы напряженности электрического поля и магнитной индукции всегда перпендикулярны друг другу, что мы будем записывать символически следующим образом: E ⟂ B .
Векторы E и B также направлены друг к другу и к направлению распространения (размножения) волн характерным образом — векторы E , B , c образуют правостороннюю систему координат (см. рисунок 6). Если мы «прикрутим» вектор E к B , как в правиле буравчика, то большой палец покажет нам направление вектора скорости волны v , или в вакууме c — то есть направление распространения.

А также стоит знать, что для любой электромагнитной волны, «бегущей» в вакууме, значения векторов напряженности электрического поля и магнитной индукции тесно связаны соотношением: E = B * c . Это не означает, что электрическое поле является каким-то привилегированным. Оба поля одинаково важны, поскольку энергия, переносимая волной, делится поровну между электрическим и магнитным полем.
Важным свойством плоской волны является постоянство ее амплитуды ( Emax, Bmax = const ) и, следовательно, постоянство интенсивности волны. Почему это происходит? Плоская волна «ходит ровным фронтом», она не рассеивается. Энергия, переносимая волной, все время падает на одну и ту же поверхность, в отличие от сферической волны, где энергия, излучаемая источником, падает на поверхность, которая увеличивается с расстоянием r от источника как r 2 .
С другой стороны, идея бесконечной поверхности по многим причинам совершенно нереальна. Можем ли мы тогда действительно иметь плоскую волну? Да, но только приблизительно. Если мы находимся далеко от передающей антенны, то волновые поверхности, создаваемые антенной, которые вблизи антенны напоминают тороидальные поверхности, становятся более плоскими по мере удаления. В конечном итоге, на большом расстоянии мы считаем поверхности плоскими, особенно когда рассматриваем небольшой участок поверхности. Тогда можно считать, что в небольшом диапазоне изменения расстояния от антенны амплитуда волны постоянна.
Вторым примером плоской (почти) электромагнитной волны может служить лазерное излучение. Луч лазерного света имеет очень небольшую расходимость.
Для справки. Лазерный луч имеет очень малое расхождение. Из всех доступных лазеров — зеленый лазер имеет самый «компактный» луч. Угол расхождения тем меньше, чем меньше длина волны лазерного излучения. Кроме того, лазерный свет монохроматичен, то есть имеет одну длину волны. Кроме того, в поперечном сечении пучка лучей лазера электрическое поле колеблется в той же фазе. Можно успешно представить, что это плоская электромагнитная волна с малой площадью волны.
Видео:Электромагнитные волны. 11 класс.Скачать

Плоская электромагнитная волна
Рассмотрим плоскую монохроматическую электромагнитную волну, распространяющуюся в направлении оси х в нейтральной (р = 0) непроводящей (/ = 0 ) среде с постоянной диэлектрической в и магнитной р проницаемостями. Другими словами, ось х перпендикулярна к волновым поверхностям, тогда значения векторов Ё и Я, а значит и их составляющие по координатным осям, не будут зависеть от координату и z.
Поэтому уравнения Максвелла в дифференциальной форме упрощаются определенным образом. Каждое из векторных уравнений (3.13.12-3.13.15) эквивалентно трем скалярным уравнениям, которые связывают компоненты векторов Ё и Н.
Например, для векторного уравнения (3.13.12) эквивалентные скалярные уравнения запишутся в виде:
С учетом заданных условий распространения волны, приведенные уравнения упрощаются:
Аналогично для векторных уравнений (3.13.13-3.13.15) получим: 
Из уравнений (4.4.11) и (4.4.12) следует, что Ех не зависит от х и от t; аналогичный результат получим из (4.4.10) и (4.4.13) для Нх. Следовательно, само поле волны не имеет составляющих вдоль оси х, т. е. векторы Ей Н перпендикулярны к направлению распространения волны, и электромагнитные волны поперечны. Предполагаем, что постоянные поля, которые могут накладываться на электромагнитное поле волны, отсутствуют и Ех = Нх = 0.
Выделим из записанных уравнений два уравнения, связывающих компоненты Еу и Hz, и два уравнения, связывающих компоненты Ez и Ну:
Можно показать, что для описания плоской электромагнитной волны можно использовать одну из систем уравнений (например, 4.4.15), положив компоненты, фигурирующие в другой системе уравнений (4.4.14), равными нулю.
Полагая Еу и Н2 равными нулю, продифференцируем первое уравнение в (4.4.15) по х:
Проведем перестановку порядка дифференцирования по координате и по времени в правой части записанного выражения и подставим
выражение, определяющее —- из второго уравнения в (4.4.15), чтобы
получить волновое уравнение для компоненты Ez:
Или, используя замену г0р0 = 4т-, запишем:
После подобных преобразований для второго уравнения в (4.4.15) получаем волновое уравнение для компоненты Ну:
Принимая во внимание принятые условия, запишем:
Решения уравнений (4.4.16) и (4.4.17) имеют вид:
Здесь со — частота, к — волновое число, к = —, cpi, ср2 — начальные
фазы колебаний Ez и Ну соответственно при значении координаты х = 0.
Подставив (4.4.18) в уравнение (4.4.15), получим:
Данные уравнения удовлетворяются при выполнении следующих условий:
Перемножив два последних равенства, запишем г0г • Е 2 т = р0рЯ^, откуда получим соотношение, связывающее амплитуды векторов Ё и Я:
Принимая cpi = ф2 = 0 и умножив уравнения (4.4.18), соответственно на единичный орт оси z и единичный орт оси у, получим уравнения плоской электромагнитной волны в векторном виде:
На рис. 4.4.1 представлена «моментальная фотография» плоской электромагнитной волны. Векторы Е и Я образуют с направлением распространения волны правовинтовую систему.
В каждой точке пространства векторы Е и Н изменяются со временем по гармоническому закону, и такие изменения векторов Е и Н происходят во всех точках пространства, но со сдвигом по фазе, который зависит от расстояния между точками, отсчитанного вдоль оси х.
Экспериментальное исследование электромагнитных волн можно проводить, используя вибратор, состоящий из двух стержней, разделенных искровым промежутком (впервые осуществлено Г. Герцем в 1888 г.). За время горения искры при подаче на вибратор высокого напряжения совершается большое число колебаний, порождающих цуг электромагнитных волн.
Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Уравнения описывающие плоскую электромагнитную волну распространяющуюся вдоль оси x
| Уравнения плоской и сферической волн |   |
Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t.
Эта функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно периодически повторяющееся движение). Кроме того, точки, отстоящие друг от друга на расстоянии l, колеблются одинаковым образом. Уравнение плоской волны Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер. Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t:
Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости
– это уравнение плоской волны. Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z. В общем виде уравнение плоской волны записывается так:
Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны. Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x. Волна, распространяющаяся в противоположном направлении, имеет вид: Уравнение волны можно записать и в другом виде. Введем волновое число
где Так как
Уравнение сферической волны В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической. Предположим, что фаза колебаний источника равна wt (т.е.
где А равна амплитуде на расстоянии от источника равном единице. Уравнение (5.2.7) неприменимо для малых r, т.к. при 🔥 ВидеоПолучение уравнения плоской бегущей волны.Скачать  Билеты № 35, 39 "Плоская волна, ее отражение. Давление излучения"Скачать  Урок 384. Излучение электромагнитных волн.Скачать  Раскрытие тайн электромагнитной волныСкачать  Билет №34 "Электромагнитные волны"Скачать  *** Лекция. Волновое уравнение электромагнитной волны ******Скачать  Вывод уравнения электромагнитной волныСкачать  Урок №45. Электромагнитные волны. Радиоволны.Скачать  Лекция 2 ВолныСкачать  Урок 370. Механические волны. Математическое описание бегущей волныСкачать  10й класс; Физика; "Уравнение плоской волны"Скачать  Электромагнитные волны в 4K (Ultra HD) 60 FPS. Как выглядит электромагнитная волнаСкачать  Парадокс электромагнитной волныСкачать  4.3 Плоские электромагнитные волны в идеальных диэлектрических средахСкачать 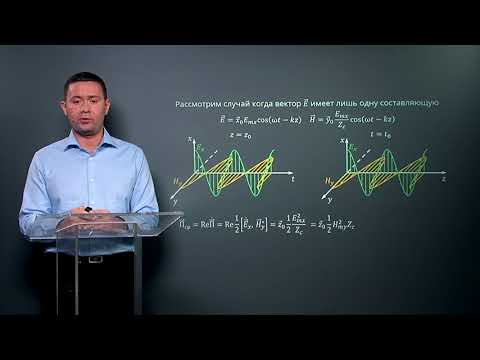 4.9 Поляризация электромагнитных волнСкачать  Электромагнитные волны и уравнения Максвелла — Эмиль АхмедовСкачать  Электромагнитные волны Лекция 10-2Скачать  Билет №41 "Отражение и преломление волн"Скачать  |















 .
. . Пусть колебание точек, лежащих в плоскости
. Пусть колебание точек, лежащих в плоскости  , имеет вид (при начальной фазе
, имеет вид (при начальной фазе  )
)

 .
. ,
, . Это будет, если энергия волны не поглощается средой.
. Это будет, если энергия волны не поглощается средой. , или
, или  .
. .
. , или в векторной форме:
, или в векторной форме: ,
, – волновой вектор,
– волновой вектор,  – нормаль к волновой поверхности.
– нормаль к волновой поверхности. , то
, то  . Отсюда
. Отсюда  . Тогда уравнение плоской волны запишется так:
. Тогда уравнение плоской волны запишется так: .
. ). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу
). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу  . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону
. Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону  . Следовательно, уравнение сферической волны:
. Следовательно, уравнение сферической волны: , или
, или  ,
, , амплитуда стремится к бесконечности. То, что амплитуда колебаний
, амплитуда стремится к бесконечности. То, что амплитуда колебаний  , следует из рассмотрения энергии, переносимой волной.
, следует из рассмотрения энергии, переносимой волной.