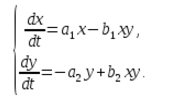Уравнения описывающие изменение численности популяции хищник y жертва x (3 видео)

Анализ модели Вольтерра «Хищник-жертва»

Южный федеральный университет

NovaInfo29
Опубликовано 21 декабря 2014
Раздел: Физико-математические науки
Просмотров за месяц: 76
CC BY-NC

Содержание

Аннотация
Ключевые слова
Текст научной работы
Модель «хищник-жертва»
Постановка задачи
Готовые работы на аналогичную тему
Решение задачи
∀ x, y, z
Экспоненциальный рост и отношения хищник—жертва
🔥 Видео

Видео:САМЫЕ ОПАСНЫЕ ОБЬЕКТЫ КОТОРЫЕ ПОХИЩАЮТ ЛЮДЕЙСкачать

Аннотация

В данной статье производится анализ системы «Хищник-жертва» при различных значениях параметров на основе компьютерного моделирования в программной среде Mathcad14.

Видео:Биология. 8 класс. Взаимоотношения «хищник-жертва». Изменение численности популяций /11.05.2021/Скачать

Ключевые слова

Видео:Модель "Хищник-жертва" в экономикеСкачать

Текст научной работы

Популяционная динамика — один из разделов математического моделирования. Интересен он тем, что имеет конкретные приложения в биологии, экологии, демографии, экономике. В данном разделе имеется несколько базовых моделей, одна из которых — модель «Хищник — жертва» — рассматривается в данной статье.

Первым примером модели в математической экологии стала модель, предложенная В.Вольтеррой. Именно он впервые рассмотрел модель взаимоотношения между хищником и жертвой.

Рассмотрим постановку задачи. Пусть имеется два вида животных, один из которых пожирает другой (хищники и жертвы). При этом принимаются следующие предположения: пищевые ресурсы жертвы не ограничены и в связи с этим в отсутствии хищника популяция жертвы возрастает по экспоненциальному закону, в то время как хищники, отделенные от своих жертв, постепенно умирают с голоду так же по экспоненциальному закону. Как только хищники и жертвы начинают обитать в непосредственной близости друг от друга, изменения численности их популяций становятся взаимосвязанными. В этом случае, очевидно, относительный прирост численности жертв будет зависеть от размеров популяции хищников, и наоборот.

В данной модели считается, что все хищники (и все жертвы) находятся в одинаковых условиях. При этом пищевые ресурсы жертв неограниченны, а хищники питаются исключительно жертвами. Обе популяции живут на ограниченной территории и не взаимодействуют с любыми другими популяциями, также отсутствуют любые другие факторы, способные повлиять на численность популяций.

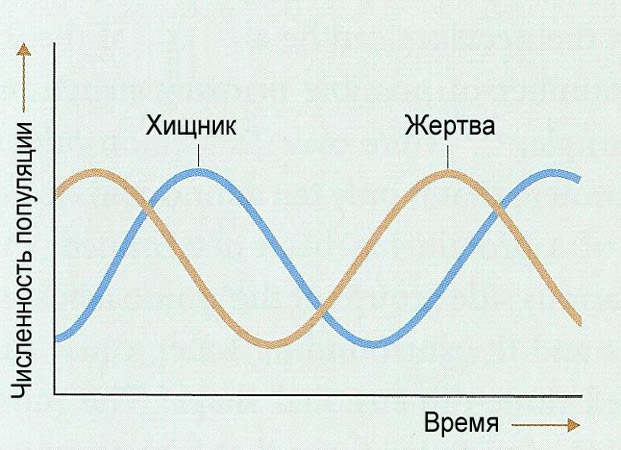
Сама математическая модель «хищник — жертва» состоит из пары дифференциальных уравнений, которые описывают динамику популяций хищников и жертв в её простейшем случае, когда имеется одна популяция хищников и одна — жертв. Модель характеризуется колебаниями в размерах обеих популяций, причём пик количества хищников немного отстаёт от пика количества жертв. С данной моделью можно ознакомиться во многих трудах по популяционной динамике или математическому моделированию. Она достаточно широко освещена и проанализирована математическими методами. Однако формулы не всегда могут дать очевидное представление о происходящем процессе.

Интересно узнать, как именно в данной модели зависит динамика популяций от начальных параметров и насколько это соответствует действительности и здравому смыслу, причём увидеть это графически, не прибегая к сложным расчётам. Для этой цели на основе модели Вольтерра была создана программа в среде Mathcad14.

Для начала проверим модель на соответствие реальным условиям. Для этого рассмотрим вырожденные случаи, когда в данных условиях обитает только одна из популяций. Теоретически было показано, что при отсутствии хищников популяция жертвы неограниченно возрастает во времени, а популяция хищника в отсутствии жертвы вымирает, что вообще говоря соответствует модели и реальной ситуации (при указанной постановке задачи).

Полученные результаты отражают теоретические: хищники постепенно вымирают(Рис.1), а численность жертвы неограниченно возрастает(Рис.2).

Рисунок 1. Зависимость числа хищников от времени при отсутствии жертвы

Рисунок 2. Зависимость числа жертв от времени при отсутствии хищников

Как видно, в данных случаях система соответствует математической модели.

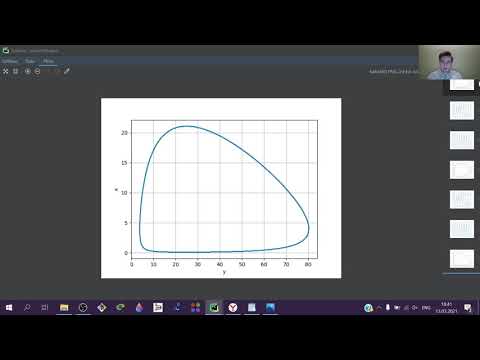
Рассмотрим, как ведёт себя система при различных начальных параметрах. Пусть имеются две популяции — львы и антилопы — хищники и жертвы соответственно, и заданы начальные показатели. Тогда получаем следующие результаты(Рис.3):

Видео:Общая биология. Взаимоотношения "хищник - жертва"Скачать

Модель «хищник-жертва»

Вы будете перенаправлены на Автор24

Часто представители одного вида (популяции) питаются представителями другого вида.

Модель Лотки – Вольтерры – модель взаимного существования двух популяций типа «хищник – жертва».

Названа в честь авторов модели – Лотка и Вольтерра, которые представили уравнения модели независимо друг от друга. Довольно распространенным является неправильное название – модель Лотки – Вольтерра.

Впервые модель «хищник – жертва» была получена А. Лоткой в 1925 году, который использовал ее для описания динамики взаимодействующих биологических популяций. В 1926 году независимо от Лотки аналогичные (к тому же более сложные) модели были разработаны итальянским математиком В. Вольтерра, глубокие исследования которого в области экологических проблем заложили фундамент математической теории биологических сообществ или т. н. математической экологии.

В математической форме предложенная система уравнений имеет вид:

где x – количество жертв, y – количество хищников, t – время, α, β, γ, δ – коэффициенты, которые отражают взаимодействия между популяциями.

Уравнения используются для моделирования системы «хищник – жертва», «паразит – хозяин», конкуренции и других видов взаимодействия между двумя видами.

Видео:Динамика биологических популяций 2Скачать

Постановка задачи

Рассмотрим закрытое пространство, в котором существуют две популяции – травоядные («жертвы») и хищники. Считается, что животных не ввозят и не вывозят и что еды для травоядных животных достаточно. Тогда уравнение изменения числа жертв (только жертв) примет вид:

Готовые работы на аналогичную тему

где $α$ – коэффициент рождаемости жертв,

$x$– размер популяции жертв,

$frac

$ – скорость прироста популяции жертв.

Когда хищники не охотятся, они могут вымирать, значит, уравнение для количества хищников (только хищников) примет вид:

, где $γ$ – коэффициент убыли хищников,

$y$ – размер популяции хищников,

$frac

$ – скорость прироста популяции хищников.

При встрече хищников и жертв (частота встреч прямо пропорциональна произведению ) хищники уничтожают жертв с коэффициентом , сытые хищники могут воспроизводить потомство с коэффициентом . Таким образом, система уравнений модели примет вид:

Видео:Факторы изменения генофонда популяции. 11 классСкачать

Решение задачи

Построим математическую модель совместного существования двух биологических популяций типа «хищник – жертва».

Пусть две биологические популяции совместно обитают в изолированной среде. Среда является стационарной и обеспечивает в неограниченном количестве всем необходимым для жизни один из видов – жертвы. Другой вид – хищник – также обитает в стационарных условиях, но питается только жертвами. В роли хищников могут выступать коты, волки, щуки, лисы, а в роли жертв – куры, зайцы, караси, мыши соответственно.

Для определенности рассмотрим в роли хищников – котов, а в роли жертв – кур.

Итак, куры и коты живут в некотором изолированном пространстве – хозяйственном дворе. Среда предоставляет курам питание в неограниченном количестве, а коты питаются только курами. Обозначим через

$х$ – количество кур,

$у$ – количество котов.

Со временем количество кур и котов меняется, но будем считать $х$ и $у$ непрерывными функциями от времени t. Назовем пару чисел $х, у)$ состоянием модели.

Найдем каким образом изменяется состояние модели $(х, у).$

Рассмотрим $frac

$ – скорость изменения количества кур.

Если котов нет, то количество кур возрастает и тем быстрее, чем больше кур. Будем считать зависимость линейной:

$a_1$ – коэффициент, который зависит только от условий жизни кур, их естественной смертности и рождаемости.

$frac

$ – скорость изменения количества котов (если нет кур), зависит от количества котов y.

Если кур нет, то количество котов уменьшается (у них нет пищи) и они вымирают. Будем считать зависимость линейной:

В экосистеме скорость изменения количества каждого вида также будем считать пропорциональным его количеству, но только с коэффициентом, зависящим от количества особей другого вида. Так, для кур этот коэффициент уменьшается с увеличением количества котов, а для котов возрастает с увеличением количества кур. Будем считать зависимость также линейной. Тогда получим систему дифференциальных уравнений:

Данная система уравнений называется моделью Вольтерра-Лотки.

a1, a2, b1, b2 – числовые коэффициенты, которые называют параметрами модели.

Как видно, характер изменения состояния модели (x, y) определяется значениями параметров. Изменяя данные параметры и решая систему уравнений модели, можно исследовать закономерности изменения состояния экологической системы.

С помощью программы MATLAB система уравнений Лотки-Вольтерра решается следующим образом:

На рис. 1 представлено решение системы. В зависимости от начальных условий решения разные, чему отвечают разные цвета траекторий.

На рис. 2 представлены те же решения, но с учетом оси времени t (т.е. наблюдается зависимость от времени).

Видео:УРОК 24-25. Моделирование в биологии (11 класс)Скачать

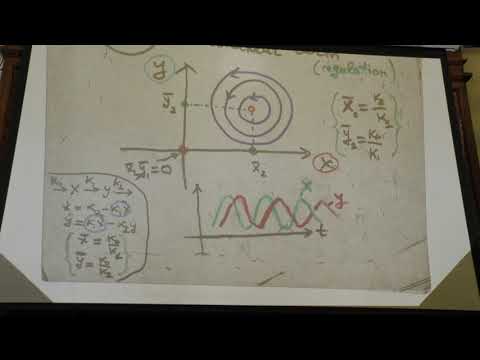
∀ x, y, z

Главная ≫ Инфотека ≫ Математика ≫ Экспоненциальный рост и отношения хищник—жертва

Видео:Рубин А. Б. - Биофизика I - Базовая модель «Хищник-жертва»Скачать

Экспоненциальный рост и отношения хищник—жертва

Комментарии: 0

Если прирост численности популяции пропорционален количеству особей, численность популяции будет расти экспоненциально.

Выражение «экспоненциальный рост» вошло в наш лексикон для обозначения быстрого, как правило безудержного увеличения. Оно часто используется, например, при описании стремительного роста числа городов или увеличения численности населения. Однако в математике этот термин имеет точный смысл и обозначает определенный вид роста.

Экспоненциальный рост имеет место в тех популяциях, в которых прирост численности (число рождений минус число смертей) пропорционален числу особей популяции. Для популяции человека, например, коэффициент рождаемости примерно пропорционален количеству репродуктивных пар, а коэффициент смертности примерно пропорционален количеству людей в популяции (обозначим его ) . Тогда, в разумном приближении,

(Здесь — так называемый коэффициент пропорциональности, который позволяет нам записать выражение пропорциональности в виде уравнения.)

Пусть — число особей, добавившихся к популяции за время , тогда если в популяции в общей сложности особей, то условия для экспоненциального роста будут удовлетворены, если

После того как в XVII веке Исаак Ньютон изобрел дифференциальное исчисление, мы знаем, как решать это уравнение для — численности популяции в любое заданное время. (Для справки: такое уравнение называется дифференциальным.) Вот его решение:

где — число особей в популяции на начало отсчета, а — время, прошедшее с этого момента. Символ обозначает такое специальное число, оно называется основание натурального логарифма (и приблизительно равно 2,7), и вся правая часть уравнения называется экспоненциальная функция.

Уравнения описывающие изменение численности популяции хищник y жертва x

Чтобы лучше понять, что такое экспоненциальный рост, представьте себе популяцию, состоящую изначально из одной бактерии. Через определенное время (через несколько часов или минут) бактерия делится надвое, тем самым удваивая размер популяции. Через следующий промежуток времени каждая из этих двух бактерий снова разделится надвое, и размер популяции вновь удвоится — теперь будет уже четыре бактерии. После десяти таких удвоений будет уже более тысячи бактерий, после двадцати — более миллиона, и так далее. Если с каждым делением популяция будет удваиваться, ее рост будет продолжаться до бесконечности.

Существует легенда (скорее всего, не соответствующая действительности), будто бы человек, который изобрел шахматы, доставил этим такое удовольствие своему султану, что тот пообещал исполнить любую его просьбу. Человек попросил, чтобы султан положил на первую клетку шахматной доски одно зерно пшеницы, на вторую — два, на третью — четыре и так далее. Султан, посчитав это требование ничтожным по сравнению с оказанной им услугой, попросил своего поданного придумать другую просьбу, но тот отказался. Естественно, к 64-му удвоению число зерен стало таким, что во всем мире не нашлось бы нужного количества пшеницы, чтобы удовлетворить эту просьбу. В той версии легенды, которая известна мне, султан в этот момент приказал отрубить голову изобретателю. Мораль, как я говорю моим студентам, такова: иногда не следует быть чересчур умным!

Пример с шахматной доской (как и с воображаемыми бактериями) показывает нам, что никакая популяция не может расти вечно. Рано или поздно она попросту исчерпает ресурсы — пространство, энергию, воду, что угодно. Поэтому популяции могут расти по экспоненциальному закону лишь некоторое время, и рано или поздно их рост должен замедлиться. Для этого нужно изменить уравнение так, чтобы при приближении численности популяции к максимально возможной (которая может поддерживаться внешней средой) скорость роста замедлялась. Назовем эту максимальную численность популяции . Тогда видоизмененное уравнение будет выглядеть так:

Когда намного меньше , членом можно пренебречь, и мы возвращаемся к первоначальному уравнению обычного экспоненциального роста. Однако когда приближается к своему максимальному значению , значение стремится к нулю, соответственно стремится к нулю и прирост численности популяции. Общая численность популяции в этом случае стабилизируется и остается на уровне . Кривая, описываемая этим уравнением, а также само уравнение, имеют несколько названий — S-кривая , логистическое уравнение, уравнение Вольтерры, уравнение Лотки—Вольтерры. (Вито Вольтерра, 1860–1940 — выдающийся итальянский математик и преподаватель; Альфред Лотка, 1880–1949 — американский математик и страховой аналитик.) Как бы она ни называлась, это — достаточно простое выражение численности популяции, резко возрастающей экспоненциально, а затем замедляющейся при приближении к некоему пределу. И она гораздо лучше отражает рост численности реальных популяций, чем обычная экспоненциальная функция.

Отношения между хищниками и их жертвами развиваются циклически, являясь иллюстрацией нейтрального равновесия.

Иногда простая математическая модель хорошо описывает сложную биологическую систему. Примером этого служат долговременные отношения между видами хищника и жертвы в какой-либо экосистеме. Математические расчеты роста популяции отдельно взятого вида (см. выше) показывают, что пределы плотности популяции можно описать простыми уравнениями, которые на выходе дают характерную S-образную кривую. Это — кривая численности популяции, которая растет экспоненциально, пока она небольшая, а затем выравнивается, когда она достигает пределов возможности экосистемы поддерживать ее. Простое продолжение этой концепции позволяет нам понять экосистему, в которой взаимодействуют два вида — хищник и жертва.

Итак, если число растительноядных жертв , а число плотоядных хищников , то вероятность, что хищник встретится с травоядным, пропорциональна произведению . Другими словами, чем выше численность одного из видов, тем выше вероятность таких встреч. В отсутствие хищников популяция жертвы будет расти экспоненциально (по крайне мере вначале), а в отсутствие жертв популяция хищника сократится до нуля — либо из-за голода, либо в результате миграции. Теперь, если — изменение популяции растительноядных за время , а изменение популяции плотоядных за тот же интервал времени, то две популяции описываются уравнениями:

Здесь — скорость роста численности травоядных в отсутствие хищников, а — скорость сокращения численности плотоядных в отсутствие травоядных. Постоянные и — скорость, с которой встречи хищников с жертвами удаляют травоядных из популяции, и скорость, с которой эти встречи позволяют хищникам прибавлять численность своей популяции. Знак минус в первом уравнении показывает, что встречи сокращают популяцию жертвы, а знак плюс во втором говорит о том, что встречи увеличивают популяцию хищника. Как видите, любое изменение численности травоядных влияет на численность плотоядных, и наоборот. Две популяции необходимо рассматривать вместе.

Решение этих уравнений показывает, что обе популяции развиваются циклически. Если популяция травоядных увеличивается, вероятность встреч хищник—жертва возрастает, и, соответственно (после некоторой временной задержки), растет популяция хищников. Но рост популяции хищников приводит к сокращению популяции травоядных (также после некоторой задержки), что ведет к снижению численности потомства хищников, а это повышает число травоядных и так далее. Эти две популяции как бы танцуют вальс во времени — когда изменяется одна из них, за ней следом изменяется и другая.

Энциклопедия Джеймса Трефила «Природа науки. 200 законов мироздания».
Джеймс Трефил — профессор физики университета Джорджа Мэйсона (США), один из наиболее известных западных авторов научно-популярных книг.