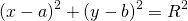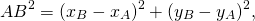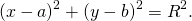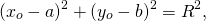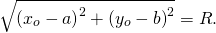Уравнение окружности с центром в точке (a;b) и радиусом R в прямоугольной системе координат имеет вид
1. Пусть в прямоугольной системе координат задана окружность с центром в точке A (a;b) и радиусом R (R>0).
Чтобы составить уравнение этой окружности, выберем на окружности произвольную точку B (x;y).
По определению окружности, расстояние от центра до любой точки окружности равно радиусу R, то есть AB=R.
Так как B (x;y) — произвольная точка окружности, координаты любой точки окружности удовлетворяют этому уравнению.
2. Если пара чисел (xo;yo) удовлетворяет данному уравнению, то
А это значит, что расстояние между точками C(xo;yo) и A(a;b) равно R. Значит, точка C(xo;yo) принадлежит окружности с центром в точке A(a;b) и радиусом R.
Следовательно, данное уравнение фигуры является уравнением окружности.
Видео:Уравнение окружности (1)Скачать
Уравнение окружности.
Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.
В формулировке окружности упоминается расстояние между точкой окружности и центром.
Формула расстояния между двумя точками М1(х1; у1) и М2(х2; у2) имеет вид:
,
Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х0; у0) и радиусом r.
Отметим произвольную точку М(х; у) на этой окружности.
.
Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.
Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х0 ) 2 +(у – у0 ) 2 = r 2 .
Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х0; у0) и радиусом r имеет вид:
В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):
Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать
Уравнение с двумя переменными и его график. Уравнение окружности
п.1. Понятие уравнения с двумя переменными
Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, (mathrm) – гипербола.
Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.
Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x 2 + 2x – y – 1 = 0 – парабола
F(x; y) = (mathrm) – y = 0 – гипербола
F(x; y)=x 2 (x + y) + y – 1 = 0 – некоторая кривая (график — ниже).
п.2. Обобщенные правила преобразования графика уравнения
Пусть F(x; y) = 0 – исходный график некоторой функции
Симметричное отображение относительно оси OY
Симметричное отображение относительно оси OX
Центральная симметрия относительно начала координат
Параллельный перенос графика на a единиц вправо
Параллельный перенос графика на a единиц влево
Параллельный перенос графика на b единиц вниз
Параллельный перенос графика на b единиц вверх
Сжатие графика к оси OY в a раз
Сжатие графика к оси OX в b раз
F(x; by) = 0
0 Например:
Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ mathrm $$
п.4. Примеры
Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: ( mathrm<y=frac=-frac + 2 > ) – это прямая
б) xy + 4 = 0
Выразим y из уравнения: ( mathrm<y=frac> ) – это гипербола
в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом ( mathrm<R=sqrt=2> )
г) x 2 + 5y – 2 = 0
Выразим y из уравнения: ( mathrm<y=frac> ) – это парабола
Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
( mathrm<y=frac=-frac25|x|+2> )
Строим график для ( mathrm ), а затем отражаем его относительно оси OY в левую полуплоскость.
б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.
в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.
г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).
д) (mathrm<frac+2|y-2|=4>)
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.
Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.
📹 Видео
№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать
На окружности с центром O отмечены точки A и B так ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать
Составляем уравнение окружностиСкачать
9 класс, 6 урок, Уравнение окружностиСкачать
№966. Напишите уравнение окружности радиуса r с центром А, если: а) А(0;5), r= 3; б) А(-1;2), r = 2Скачать
ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать
№965. Напишите уравнения окружностей с центром в начале координат и радиусами r1=3, r2= √2 , r3=5/2.Скачать
Уравнение окружности с центром на оси абсцисс, ординат или в начале координат. Урок 3. Геометрия 8.Скачать
Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать
начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать
2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать
УРАВНЕНИЕ ОКРУЖНОСТИСкачать
Уравнение окружностиСкачать
2184 касательная в точках A и B к окружности с центром О пересекаютсяСкачать
№145. Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружностиСкачать
№969. Напишите уравнение окружности с диаметром MN, если: а) М (-3; 5),Скачать
ПРОСТОЙ СЕКРЕТ ДЛЯ НАЧИНАЮЩИХ! Реши алгебру за 12 минут — Уравнение ОкружностиСкачать
