Рассмотрим линейное пространство V, в котором каждому элементу x, в силу
некоторого закона поставлен элемент этого же пространства.


Каждому прообразу соответствует единственный образ.
Каждый образ имеет единственный прообраз.
Линейное преобразование пространства, при котором существует
Блективное преобразование – 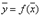
1.
2.
Рассмотрим n-мерное линейное пространство
Для того, чтобы задать линейные преобразования в этом пространстве достаточно
задать это преобразование для базисных векторов.

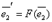

Матрица линейного преобразования.
Пусть F – линейное преобразование линейного пространства, переводящая базис
в базис 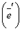
— базис, то верны соотношения
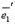
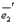

А – является матрицей линейного преобразования или линейным оператором
Связь между координатами образа и прообраза.
В базисе 

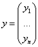

Линейное преобразование – матрица линейного оператора.
Каждому линейному преобразованию соответствует 1 матрица линейного оператора
Если имеется квадратная матрица 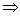
17. Связь между координатами одного и того же линейного оператора в
Разных базисах.

Т – матрица перехода от e к e’ , то:

Если линейный оператор имеет в базисе невырожденную матрицу Т, матрица этого
оператора в любом другом базисе не будет вырождена.
18. Характеристическое уравнение линейного оператора. Собственные
Векторы линейного оператора и их свойства.
Если в базисе 
) оператор имеет матрицу В
λ – произвольное число ≠0
Е – единичная матрица

характеристически многочлен линейного оператора прировнять к 0, получим
характеристическое уравнение линейного оператора.
Собственные векторы линейного оператора
Ненулевой вектор
называется собственным вектором линейного оператора, если
оператор к 
этот же 
умноженный на некоторое к.
к – собственное число оператора А=
Каждый собственный вектор имеет единственное собственное число.
19. Прямая в пространстве. Виды уравнений прямой. Угол между прямыми.
Векторное уравнение прямой.
Положение прямой можно задать по точке и направляющему вектору.
Пусть прямая L задана ее точкой M0(x0;y0;z
0) и направляющим вектором S(m;n;p). Возьмем на прямой L точку M(x;y;z).
Обозначим радиус-векторы точек M и M0 через r и r0.
Тогда уравнение прямой запишется в виде:
где t – скалярный множитель (параметр).
Параметрические уравнения прямой.
Канонические уравнения прямой.
;z0) – точка на прямой.
соединяет M0 с произвольной точкой М.
Уравнение прямой в пространстве, проходящей через две точки.
В качестве направляющего вектора можно задать вектор

Общее уравнение прямой.
Уравнение прямой как линию пересечения двух плоскостей. Рассмотрим:
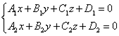
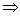
Т.к. прямая перпендикулярна векторам n1 и n2 то
направляющий вектор запишется как векторное произведение:
Угол между прямыми.
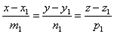
20. Плоскость в пространстве. Виды уравнения плоскостей. Угол между плоскостями.
Уравнение плоскости, проходящей через заданную точку, перпендикулярно данному
) и вектором 
перпендикулярной этой плоскости.
Возьмем произвольную точку M(x;y;z) и составим вектор
. При любом расположении точки М на плоскости Q
, поэтому 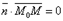
Общее уравнение плоскости.
· Если D=0, то данному уравнению удовлетворяет точка О (0;0;0)
· Если С=0 то вектор
. Следовательно, плоскость параллельна оси oz, если В=0 – то oy, если А=0 – то
· Если C=D=0, то плоскость проходит через О (0;0;0), параллельно оси oz.
Аналогично при A=D=0 и B=D=0.
· Если А=В=0 то уравнение примет вид 
· Если A=B=D=0, то уравнение имеет вид 
Уравнение плоскости, проходящей через три точки
Возьмем на плоскости точку P (x;y;z).
Эти векторы лежат в одной плоскости, следовательно они компланарны:
Уравнение плоскости в отрезках.
Пусть плоскость отсекает на осях отрезки, т.е. проходит через точки:
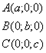
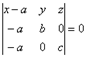
Нормальное уравнение плоскости.
21. Угол между прямой и плоскостью. Расстояние от точки до плоскости.
Прямая L:
Пусть φ – угол между плоскостью и прямой.
Тогда θ – угол между 

Найдем 

Расстояние от точки до плоскости.
Расстояние d от точки М0 до плоскости ∆ равно модулю проекции
вектора 
плоскости) на направление нормального вектора
. Если плоскость задана уравнением:
то расстояние до плоскости находится по формуле:
22. Прямая на плоскости. Виды уравнений прямой на плоскости. Угол между
Двумя прямыми.
Уравнение с угловым коэффициентом.
k= tg α – угловой коэффициент.
Если b=0 то прямая проходит через начало координат. Уравнение примет вид
Если α=0, то k = tg α = 0. То прямая пройдет параллельно оси ох.
Если α=π/2, то уравнение теряет смысл. В этом случае уравнение примет
вид 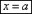
параллельно оси оу.
Общее уравнение прямой.
A, B, C – произвольные числа, причем А и В не равны нулю одновременно.
· Если В=0, то уравнение имеет вид
или 
прямой, параллельной оси оу. и проходящей через точку
· Если В≠0, то получаем уравнение с угловым коэффициентом 

· Если С=0, то уравнение проходит через т. О (0;0).
Уравнение прямой, проходящей через точку, в данном направлении.
Уравнение прямой записывается в виде 
Подставим в это уравнение точку М

Уравнение прямой, проходящей через 2 точки.
Уравнение прямой в отрезках.
Подставим точки в уравнение прямой:
Уравнение прямой, проходящей через данную точку, перпендикулярно данному
М0 (х0;у0).
Возьмем произвольную точку М (х;у).
Т.к. 
Нормальное уравнение прямой.
Уравнение прямой можно записать в виде:
Т.к. 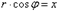
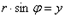
Угол между прямыми.
Дано: прямые L1 и L2 с угловыми коэффициентами
Требуется найти угол между прямыми:
23. Эллипс. Определение. Вывод канонического уравнения.

геометрическое место всех
точек плоскости, сумма
расстояний от которых до
до фокусов есть величина
постоянная, большая, чем расстояние между фокусами.
Пусть М (х;у) – произвольная точка эллипса.
Т.к.
То получаем
Или
24. Гипербола. Определение. Вывод канонического уравнения.
Гиперболой называется множество всех точек плоскости, модуль разности
расстояний от каждой из которых до фокусов есть величина постоянная.
Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению

25. Парабола. Определение. Вывод канонического уравнения.
Парабола – множество всех точек плоскости, каждая из которых одинаково
удалена от фокуса, и директрисы. Расстояние между фокусом и директрисой
называется параметром параболы и обозначается через р>0.

точка M с F. Проведем отрезок
26. Поверхности вращения.
Поверхность, образованная вращением некоторой плоской кривой вокруг оси,
лежащей в ее плоскости, называется поверхностью вращения. Пусть некоторая
кривая L лежит в плоскости Oyz. Уравнение этой кривой запишутся в виде:
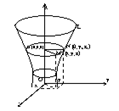
Возьмем на поверхности точку
M (x;y;z). Проведем через точку
М плоскость, перпендикулярную
оси oz, и обозначим точки
пересечения ее с осью oz
и кривой L соответственно O1 и N.
Обозначим координаты точки
являются радиусами одной и той же окружности. Поэтому O1M = O1
N. Но O1M = (x 2 +y 2 ) 0.5 , O1
Следовательно, |y1|=(x 2 +y 2 ) 0.5 или y1=±(x 2 +y 2 ) 0.5 . Кроме того, очевидно, z1=z.
Следовательно 
искомое уравнение поверхности вращения, ему удовлетворяют координаты любой
точка М этой поверхности и не удовлетворяет координаты точек, не лежащих на
27. Поверхности 2-го порядка. Эллипсоид, Гиперболоид.
Рассмотрим сечение поверхности с плоскостями, параллельными xOy. Уравнения
таких плоскостей z=h, где h – любое число. Линия, получаемая в сечении,
определяется двумя уравнениями:
Если |h|>c, c>0, то 
Если |h|=c, т.е. h=±c, то
. Линия пересечения вырождается в две точки (0;0;с) и (0;0;-с). Плоскости z=c и
z=–c касаются поверхности.
Если |h| 2 +y 2 +z 2 =R 2
Пересекая поверхность плоскостью z=h, получим линию пересечения, уравнения
которой имеют вид.

Полуоси достигают своего наименьшего значения при h=0, a1=a, b1
=b. При возрастании |h| полуоси будут увеличиваться.
Если пересекать поверхность плоскостями x=h или y=h, то в сечении получим
гиперболы. Найдем линию пересечения поверхности с плоскостью Oyx, уравнение
которой x=0. Эта линия пересечения описывается уравнениями:
Поверхность имеет форму бесконечно расширяющейся трубки и называется
однополостным гиперболоидом.
Если поверхность пересечь плоскостями z=h, то линия пересечение уравнениями
Если |h| c, то уравнения можно переписать в виде:
Эти уравнения определяют эллипс, полуоси которого возрастают с ростом |h|.
У обеих гипербол действительной осью является ось oz. Метод сечения позволяет
изобразить поверхность, состоящую из двух полостей, имеющих форму двух
неограниченных чаш. Поверхность называется двуполостным гиперболоидом.
28. Поверхности 2-го порядка. Параболоиды.
При пересечении поверхности координатами плоскостями Oxz и Oyz получается
соответственно параболы
и 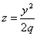
поверхность, определяемая уравнением, имеет вид выпуклой, бесконечно
Рассечем поверхность плоскостями z=h. Получим кривую
которая при всех h≠0 является гиперболой. При h>0 ее действительные оси
параллельны оси Ox, при h 2 +Cy 2 +2Dx+2Ey+F=0 всегда определяет либо
окружность (при А=С), либо эллипс (при А*С>0), либо гиперболу (при
А*С 2 +2Bxy+Cy 2 +2Dx+2Ey+F=0
Коэффициент В с произведением координат преобразовывает уравнение путем
поворота координатных осей.
31. Определение предела числовой функции. Односторонние пределы.
Свойства пределов.
Число А называется пределом функции y=f(x) в точке х0, если для любой
последовательности допустимых значений аргумента xn, n?N (xn
(т.е. 
последовательность соответствующих значений функции f(xn), n?N,
сходится к числу А, т.е.
. Геометрический смысл предела этой функции, что для всех точек х, достаточно
близких к точке х0, соответствующие значения функции как угодно мало
отличается от числа А.
Считается, что х стремится к х0 любым способом: оставаясь меньшим,
чем х0 (слева от х0), большим, чем х0 (справа
от х0), или колеблясь около точки х0.
Число А1 называется пределом функции y=f(x) слева в
точке х0, если для любого ε 0 такое, что при х?(x0-σ;x0
), выполняется неравенство |f(x)-A1|
- Решение задач с помощью аффинных преобразований
- Уравнение прямой, виды уравнения прямой на плоскости
- Определение уравнения прямой на плоскости
- Общее уравнение прямой линии
- Уравнение прямой в отрезках
- Уравнение прямой с угловым коэффициентом
- Каноническое уравнение прямой на плоскости
- Параметрические уравнения прямой на плоскости
- Нормальное уравнение прямой
- 🎬 Видео
Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Решение задач с помощью аффинных преобразований
Разделы: Математика
Для начала: на чем основывается метод решения с помощью аффинных преобразований?
Необходим некий краткий теоретический материал для учащихся.
Сообщаем, что система координат не обязательно должна быть прямоугольной. Если выбрать на плоскости 3 точки 



Сообщаем, что система координат не обязательно должна быть прямоугольной. Если выбрать на плоскости 3 точки 



Определение 1. Пусть в плоскостях 













Свойства аффинных преобразований:
1) По свойствам координат аффинное преобразование является взаимно однозначным отображением плоскости на плоскость:
— каждая точка имеет образ и притом только один;
— разные точки имеют разные образы;
— каждая точка области значений имеет прообраз.
2) Так как аффинное отображение сохраняет координаты точек, то оно сохраняет уравнения фигур. Отсюда следует, что прямая переходит в прямую.
3) Преобразование, обратное к аффинному, есть снова аффинное преобразование.
4) Точки, не лежащие на одной прямой, переходят в точки, не лежащие на одной прямой, а, значит, пересекающиеся прямые — в пересекающиеся прямые, а параллельные – в параллельные.
5) При аффинных преобразованиях сохраняются отношения длин отрезков, лежащих на одной или параллельных прямых.
6) Отношения площадей многоугольников также сохраняются.
7) Не обязательно сохраняются отношения длин отрезков непараллельных прямых, углы.
Замечание 1: Если А, В, С — три точки плоскости, не лежащие на одной прямой, а 

Замечание 2: Параллельное проектирование есть аффинное преобразование плоскости на плоскость. Кстати эта тема “Параллельное проектирование” присутствует в школьном учебнике геометрии 10-11(2000) Л. С. Атанасяна в приложении 1. В основном этот материал используется тогда, когда мы учим изображать пространственные фигуры на плоскости.
Чтобы представить, что могут аффинные преобразования, посмотрим картинки. Учащимся лучше всего именно наглядно показать применение аффинных преобразований на отвлеченном предмете и только потом переходить на геометрические фигуры.
Частным случаем аффинных преобразований являются преобразование подобия, гомотетия и движения. Движения — это параллельные переносы, повороты, различные симметрии и их комбинации. Другой важный случай аффинных преобразований — это растяжения и сжатия относительно прямой. На рисунке 2 показаны различные движения плоскости с нарисованным на ней домиком. А на рисунке 3 и 4 показаны различные аффинные преобразования этой плоскости (параллельное проектирование).
А вот на следующей картинке можно объяснить суть метода.
Если перед вами стоит задача о вычислении каких-то соотношений или пропорций на искаженном рисунке, например: найти отношение длины ушей к длине хвоста, то можно найти это отношение на более удобном рисунке (неискаженном), что намного проще, и найденное решение будет соответствовать и искаженному рисунку в том числе. Но нельзя искать отношение, например, длины ушей к толщине зайца, т.к. это отрезки непараллельных прямых.
Теперь перейдем к геометрическим фигурам. Как на них может работать этот метод?
Обычно, задачу можно решить методом аффинных преобразований, если нужно найти отношение длин, отношение площадей, доказать параллельность или принадлежность точек одной прямой. Причем в условии задачи не должны содержаться данные, не сохраняющиеся при аффинных преобразованиях.
Свойства фигур называются аффинными, если они сохраняются при аффинных отображениях. Например, быть медианой треугольника- это аффинное свойство (середина стороны переходит в середину при аффинном отображении), а быть биссектрисой – нет.
Суть метода при решении геометрических задач.
Часто бывает удобно при решении задач на аффинные свойства перейти с помощью аффинных преобразований к более простым фигурам, например, к правильному треугольнику. А затем с помощью обратного аффинного преобразования перенести полученный результат на искомую фигуру.
Для начала можно решить всем известную задачу о точке пересечения медиан треугольника.
Задача 1. Доказать, что медианы произвольного треугольника пересекаются в одной точке и делятся в отношении 2:1, считая от вершины.
Решение (по алгоритму).
Пусть дан треугольник ABC. 1) Проверим аффинные свойства фигуры. Треугольник (по замечанию 1) является аффинной фигурой, быть медианой — это тоже аффинное свойство и отношения длин отрезков также сохраняется при аффинном отображении.
2) Значит, можно перейти к более удобной фигуре — равностороннему треугольнику.
3) Возьмем равносторонний треугольник 






4) Зададим аффинное отображение, переводящее треугольник 

5) Утверждение для произвольного треугольника доказано.
Задача 2. Доказать, что в любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой.
Пусть дана трапеция ABCD, в которой M и N – середины оснований, Q – точка пересечения диагоналей, О – точка пересечения продолжений боковых сторон.
1) Проверим аффинные свойства фигуры. Трапеция — аффинная фигура (так как трапеция переходит в трапецию), принадлежность точек одной прямой является аффинным свойством. Таким образом, и условие, и вопрос задачи относятся к аффинному классу задач. Значит, можно применить метод аффинных преобразований.
2) Возьмем произвольный равнобедренный треугольник 








3) Доказать сформулированную задачу для равнобокой трапеции труда не составит (при чем не одним способом).
4) Таким образом, доказав, что точки 



5) Доказанный факт справедлив и для произвольной трапеции.
Примечание. Четырехугольники аффинно эквивалентны тогда и только тогда, когда точка пересечения диагоналей делит их в одном и том же отношении.
Задача 3 (из диагностической работы по подготовке к ЕГЭ-2010). Через точку О, лежащую в треугольнике АВС, проведены три прямые, параллельные всем сторонам треугольника. В результате треугольник разбился на 3 треугольника и 3 параллелограмма. Известно, что площади полученных треугольников равны соответственно 1; 2.25 и 4. Найдите сумму площадей полученных параллелограммов (задача из диагностической работы по подготовке к ЕГЭ — 2010)
Решение, предложенное авторами
Но эту задачу легко решить с помощью аффинных преобразований.
- Проверим аффинные свойства фигуры. Треугольник является аффинной фигурой, параллельность также относится к аффинным свойствам. Так как известны площади, можно найти их отношение, которое будет сохраняться при аффинных преобразованиях.
- Пусть даны два треугольника: произвольный и равносторонний. Решить задачу на равностороннем треугольнике намного проще. Возьмем аффинное отображение, переводящее произвольный треугольник в равносторонний.
- Решаем задачу на равностороннем.
Треугольники, получившиеся внутри нашего равностороннего, являются подобными (по 2 углам). Следовательно, их площади относятся как квадрат коэффициента подобия, обозначим 







По свойствам аффинных отображений решение справедливо и для произвольного треугольника.
Мы рассмотрели планиметрические задачи, но свойства аффинных преобразований работают и в пространстве. Например, образом тетраэдра может служить произвольный заранее выбранный тетраэдр. У любого параллелепипеда аффинным образом может быть куб.
Задача 4 (стереометрическая). Докажите, что диагональ 



Это №372 из учебника Атанасяна (11 класс). В учебнике дано ее решение векторным методом. Но можно применить метод аффинных преобразований, решив эту задачу на кубе уже в 10 классе.
В этой задаче с помощью аффинных преобразований докажем равенство трех отрезков.
1) Проверим аффинные свойства фигуры и условия задачи. Аффинным образом любого параллелепипеда может быть куб. Деление отрезка в заданном отношении – это аффинное свойство.
2) Рассмотрим одноименный куб 



3) Докажем, что диагональ делится этими точками на три равных отрезка.
1. Рассмотрим пирамиду 





















2. Аналогично найдем 


3. Из треугольника 


4. Вычислим 




5. Получили 





4) Существует аффинное отображение, переводящее куб в произвольный параллелепипед. Значит, эта задача будет верна и для произвольного параллелепипеда.
5) Обобщения. Какие свойства, доказанные на кубе, сохранятся для произвольного параллелепипеда, а какие нет (обсудить с учащимися).
Например: параллельность плоскостей и отношение сохранится, перпендикулярность диагонали плоскостям нет, правильные треугольники не сохранятся, так же как и центр правильного треугольника, он перейдет в точку пересечения медиан.
Таким образом, уже в 10 классе можно делать с учащимися обобщения для произвольных фигур, пользуясь свойствами аффинных отображений.
Мы рассмотрели задачи программного уровня, а теперь рассмотрим задачи продвинутого уровня.
Вот задача, предложенная учащимся 11-го класса на олимпиаде в этом году. Никто, к сожалению, с ней не справился. Посмотрим, как метод аффинных преобразований поможет нам ее решить.
Задача 5 (олимпиада 11 класс). Треугольная пирамида рассечена плоскостью так, что медианы боковых граней разбиты точками пересечения в отношении 2:1,3:1 и 4:1, считая от вершины пирамиды. В каком отношении, считая от вершины пирамиды, разбиты боковые рёбра? (Из материалов МГТУ им. Баумана). Ответ: 12:7 , 12:5, 12:1
Существует решение, предложенное авторами. В этом решении отсутствуют различные подробные вычисления, поэтому по объему решение недлинное, о сложности будете судить сами.
А решение с помощью аффинных преобразований мы рассмотрим.
1) В задаче фигурирует произвольная пирамида, в которой проведены медианы (а быть медианой — это аффинное свойство), на медианах взяты пропорциональные отрезки ( при аффинном преобразовании сохраняются отношения длин отрезков, лежащих на одной прямой). Значит, эту задачу можно решить для “удобной” пирамиды, а затем с помощью аффинного преобразования перенести результат на произвольную.
2) Решим задачу для пирамиды, у которой три плоских угла при вершине прямые. Поместим новую пирамиду в прямоугольную систему координат OXYZ.
3) Проведем медиану 
















Итак: К


N 
Анализируя, выберем сами удобные числовые координаты для точек А(40;0;0), В(0;15;0), С(0;0;24).
Плоскость (MNK) пересекает ребра пирамиды в неких точках 
















Нам надо найти отношение 

Решив задачу на “удобной” пирамиде, учитывая, что существует аффинное преобразование, переводящее эту пирамиду в произвольную, переносим результат на произвольную пирамиду.
Если бы в условии данной задачи была предложена “удобная” пирамида, наверное, кто-то из учеников сделал хотя бы попытки решить задачу.Метод аффинных преобразований позволяет трудные факты свести к легкому доказательству.
Например, доказать следующую задачу 6: Пусть заданы два треугольника АВС и 
Любой четырехугольник может рассматриваться, как образ тетраэдра при параллельной проекции на плоскость. Рассмотрим четырехугольник SABС.
Существует аффинное преобразование f, переводящее его в четырехугольник 








Построение.1) 

В пересечении плоскостей три точки, следовательно, они лежат на одной прямой. Эта задача (теорема Дезарга) доказана.
В продолжение такого применения аффинных преобразований (решение пространственной задачи как планиметрической) можно рассмотреть еще одну интересную задачу.
Задача (Соросовская олимпиада)
Даны три луча 
То есть картинка должна быть примерно такая.
Будем рассматривать эту картинку как аффинный образ (при некотором аффинном отображении) пирамиды XOYZ на плоскость. Вершины пирамиды лежат на осях координат, а точки А, В, С — точки в координатных плоскостях. Тогда задача сводится к тому, чтобы построить линии пересечения плоскости (АВС) с координатными плоскостями. Существует, конечно, способ построения с помощью циркуля и линейки, но нам он не нужен. Итак, без циркуля.
- Возьмем произвольную точку S на луче
.
- Проведем прямые
и
.
,
.
, такая, что Р и С лежат в одной плоскости.
,
- ZY,
- XYZ — искомый треугольник.
Выводы.
Итак, вам был представлен метод решения задач с помощью аффинных преобразований. Подведем итоги.
- Метод позволяет перейти от более сложного к более простому для осуществления процесса решения.
- Носит обобщающий характер.
- Имеет широкую область применения, в том числе в смежных областях.
- Позволяет интегрировать разные разделы математики.
- Осмысление и применение данного метода формирует у учащихся конструктивный подход к решению задач и критичность мышления.
Видео:УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Уравнение прямой, виды уравнения прямой на плоскости
В прошлом материале мы рассмотрели основные моменты, касающиеся темы прямой на плоскости. Теперь же перейдем к изучению уравнения прямой: рассмотрим, какое уравнение может называться уравнением прямой, а также то, какой вид имеет уравнение прямой на плоскости.
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Определение уравнения прямой на плоскости
Допустим, что есть прямая линия, которая задана в прямоугольной декартовой системе координат O х у .
Прямая линия – это геометрическая фигура, которая состоит из точек. Каждая точка имеет свои координаты по осям абсцисс и ординат. Уравнение, которое описывает зависимость координат каждой точки прямой в декартовой системе O x y , называется уравнением прямой на плоскости.
Фактически, уравнение прямой на плоскости – это уравнение с двумя переменными, которые обозначаются как x и y . Уравнение обращается в тождество при подстановке в него значений любой из точек прямой линии.
Давайте посмотрим, какой вид будет иметь уравнение прямой на плоскости. Этому будет посвящен весь следующий раздел нашей статьи. Отметим, что существует несколько вариантов записи уравнения прямой. Объясняется это наличием нескольких способов задания прямой линии на плоскости, и также различной спецификой задач.
Видео:Уравнение прямой на плоскостиСкачать

Общее уравнение прямой линии
Познакомимся с теоремой, которая задает вид уравнения прямой линии на плоскости в декартовой системе координат O x y .
Уравнение вида A x + B y + C = 0 , где x и y – переменные, а А , В и C – это некоторые действительные числа, из которых A и B не равны нулю, задает прямую линию в декартовой системе координат O x y . В свою очередь, любая прямая линия на плоскости может быть задана уравнением вида A x + B y + C = 0 .
Таким образом, общее уравнение прямой на плоскости имеет вид A x + B y + C = 0 .
Поясним некоторые важные аспекты темы.
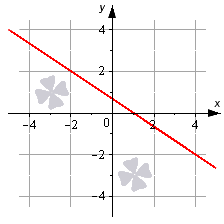
Посмотрите на рисунок.
Линия на чертеже определяется уравнением вида 2 x + 3 y — 2 = 0 , так как координаты любой точки, составляющей эту прямую, удовлетворяют приведенному уравнению. В то же время, определенное количество точек плоскости, определяемых уравнением 2 x + 3 y — 2 = 0 , дают нам прямую линию, которую мы видим на рисунке.
Общее уравнение прямой может быть полным и неполным. В полном уравнении все числа А , В и C отличны от нуля. Во всех остальных случаях уравнение считается неполным. Уравнение вида A x + B y = 0 определяет прямую линию, которая проходит через начало координат. Если A равно нулю, то уравнение A x + B y + C = 0 задает прямую, расположенную параллельно оси абсцисс O x . Если B равно нулю, то линия параллельна оси ординат O y .
Вывод: при некотором наборе значений чисел А , В и C с помощью общего уравнения прямой можно записать любую прямую линию на плоскости в прямоугольной системе координат O х у .
Прямая, заданная уравнением вида A x + B y + C = 0 , имеет нормальный вектор прямой с координатами A , B .
Все приведенные уравнения прямых, которые мы рассмотрим ниже, могут быть получены из общего уравнения прямой. Также возможен и обратный процесс, когда любое из рассматриваемых уравнений может быть приведено к общему уравнению прямой.
Разобраться во всех нюансах темы можно в статье «Общее уравнение прямой». В материале мы приводим доказательство теоремы с графическими иллюстрациями и подробным разбором примеров. Особое внимание в статье уделяется переходам от общего уравнения прямой к уравнениям других видов и обратно.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Уравнение прямой в отрезках
Уравнение прямой в отрезках имеет вид x a + y b = 1 , где a и b – это некоторые действительные числа, которые не равны нулю. Абсолютные величины чисел a и b равны длине отрезков, которые отсекаются прямой линией на осях координат. Длина отрезков отсчитывается от начала координат.
Благодаря уравнению можно легко построить прямую линию на чертеже. Для этого необходимо отметить в прямоугольной системе координат точки a , 0 и 0 , b , а затем соединить их прямой линией.
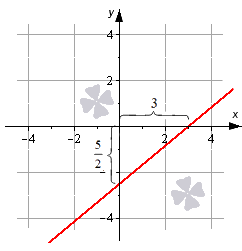
Построим прямую, которая задана формулой x 3 + y — 5 2 = 1 . Отмечаем на графике две точки 3 , 0 , 0 , — 5 2 , соединяем их между собой.
Дополнительно рекомендуем ознакомиться с материалом, изложенным в статье «Уравнение прямой в отрезках».
Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать

Уравнение прямой с угловым коэффициентом
Эти уравнения, имеющие вид y = k · x + b должны быть нам хорошо известны из курса алгебры. Здесь x и y – это переменные, k и b – это некоторые действительные числа, из которых k представляет собой угловой коэффициент. В этих уравнениях переменная у является функцией аргумента x .
Дадим определение углового коэффициента через определение угла наклона прямой к положительному направлению оси O x .
Для обозначения угла наклона прямой к положительному направлению оси O x в декартовой системе координат введем величину угла α . Угол отсчитывается от положительного направления оси абсцисс до прямой линии против хода часовой стрелки. Угол α считается равным нулю в том случае, если линия параллельна оси O x или совпадает с ней.
Угловой коэффициент прямой – это тангенс угла наклона этой прямой. Записывается это следующим образом k = t g α . Для прямой, которая располагается параллельно оси O y или совпадает с ней, записать уравнение прямой с угловым коэффициентом не представляется возможным, так как угловой коэффициент в этом случае превращается в бесконечность (не существует).
Прямая, которая задана уравнением y = k · x + b , проходит через точку 0 , b на оси ординат. Это значит, что уравнение прямой с угловым коэффициентом y = k · x + b , задает на плоскости прямую линию, которая проходит через точку 0 , b и образует угол α с положительным направлением оси O x , причем k = t g α .
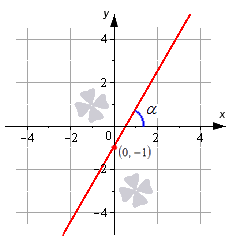
Изобразим прямую линию, которая определяется уравнением вида y = 3 · x — 1 .
Эта линия должна пройти через точку ( 0 , — 1 ) . Угол наклона α = a r c t g 3 = π 3 равен 60 градусов к положительному направлению оси O x . Угловой коэффициент равен 3
Обращаем ваше внимание, что с помощью уравнения прямой с угловым коэффициентом очень удобно искать уравнение касательной к графику функции в точке.
Больше материала по теме можно найти в статье «Уравнение прямой с угловым коэффициентом». Помимо теории там размещено большое количество графических примеров и подробный разбор задач.
Видео:Уравнения прямой на плоскости | Векторная алгебраСкачать

Каноническое уравнение прямой на плоскости
Данный вид уравнения имеет вид x — x 1 a x = y — y 1 a y , где x 1 , y 1 , a x , a y — это некоторые действительные числа, из которых a x и a y не равны нулю.
Прямая линия, заданная каноническим уравнением прямой, проходит через точку M 1 ( x 1 , y 1 ) . Числа a x и a y в знаменателях дробей представляют собой координаты направляющего вектора прямой линии. Это значит, что каноническое уравнение прямой линии x — x 1 a x = y — y 1 a y в декартовой системе координат O x y соответствует линии, проходящей через точку M 1 ( x 1 , y 1 ) и имеющей направляющий вектор a → = ( a x , a y ) .
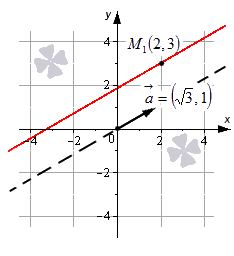
Изобразим в системе координат O x y прямую линию, которая задается уравнением x — 2 3 = y — 3 1 . Точка M 1 ( 2 , 3 ) принадлежит прямой, вектор a → ( 3 , 1 ) является направляющим вектором этой прямой линии.
Каноническое уравнение прямой линии вида x — x 1 a x = y — y 1 a y может быть использовано в случаях, когда a x или a y равно нулю. Наличие ноля в знаменателе делает запись x — x 1 a x = y — y 1 a y условной. Уравнение можно записать следующим образом a y ( x — x 1 ) = a x ( y — y 1 ) .
В том случае, когда a x = 0 , каноническое уравнение прямой принимает вид x — x 1 0 = y — y 1 a y и задает прямую линию, которая расположена параллельно оси ординат или совпадает с этой осью.
Каноническое уравнение прямой при условии, что a y = 0 , принимает вид x — x 1 a x = y — y 1 0 . Такое уравнение задает прямую линию, расположенную параллельно оси абсцисс или совпадающую с ней.
Больше материала на тему канонического уравнения прямой смотрите здесь. В статье мы приводим целый ряд решений задач, а также многочисленные примеры, которые позволяют лучше овладеть темой.
Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Параметрические уравнения прямой на плоскости
Данные уравнения имеют вид x = x 1 + a x · λ y = y 1 + a y · λ , где x 1 , y 1 , a x , a y — это некоторые действительные числа, из которых a x и a y не могут быть одновременно равны нулю. В формулу вводится дополнительный параметр λ , который может принимать любые действительные значения.
Назначение параметрического уравнения в том, чтобы установить неявную зависимости между координатами точек прямой линии. Для этого и вводится параметр λ .
Числа x , y представляют собой координаты некоторой точки прямой. Они вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра λ .
Предположим, что λ = 0 .
Тогда x = x 1 + a x · 0 y = y 1 + a y · 0 ⇔ x = x 1 y = y 1 , т. е. точка с координатами ( x 1 , y 1 ) принадлежит прямой.
Обращаем ваше внимание на то, что коэффициенты a x и a y при параметре λ в данном виде уравнений представляют собой координаты направляющего вектора прямой линии.
Рассмотрим параметрические уравнения прямой линии вида x = 2 + 3 · λ y = 3 + λ . Прямая, заданная уравнениями, в декартовой системе координат проходит через точку ( x 1 , y 1 ) и имеет направляющий вектор a → = ( 3 , 1 ) .
Больше информации ищите в статье «Параметрические уравнения прямой на плоскости».
Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Нормальное уравнение прямой
Нормальное уравнение прямой имеет вид , A x + B y + C = 0 , где числа А , В , и C таковы, что длина вектора n → = ( A , B ) равна единице, а C ≤ 0 .
Нормальным вектором линии, заданной нормальным уравнением прямой в прямоугольной системе координат O х у , является вектор n → = ( A , B ) . Эта прямая проходит на расстоянии C от начала координат в направлении вектора n → = ( A , B ) .
Еще одним вариантом записи нормального уравнения прямой линии является cos α · x + cos β · y — p = 0 , где cos α и cos β — это два действительных числа, которые представляют собой направляющие косинусы нормального вектора прямой единичной длины. Это значит, что n → = ( cos α , cos β ) , справедливо равенство n → = cos 2 α + cos 2 β = 1 , величина p ≥ 0 и равна расстоянию от начала координат до прямой.
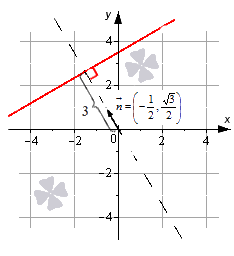
Рассмотрим общее уравнение прямой — 1 2 · x + 3 2 · y — 3 = 0 . Это общее уравнение прямой является нормальным уравнением прямой, так как n → = A 2 + B 2 = — 1 2 2 + 3 2 = 1 и C = — 3 ≤ 0 .
Уравнение задает в декартовой системе координат 0ху прямую линию, нормальный вектор которой имеет координаты — 1 2 , 3 2 . Линия удалена от начала координат на 3 единицы в направлении нормального вектора n → = — 1 2 , 3 2 .
Обращаем ваше внимание на то, что нормальное уравнение прямой на плоскости позволяет находить расстояние от точки до прямой на плоскости.
Если в общем уравнении прямой A x + B y + C = 0 числа А , В и С таковы, что уравнение A x + B y + C = 0 не является нормальным уравнением прямой, то его можно привести к нормальному виду. Подробнее об этом читайте в статье «Нормальное уравнение прямой».
🎬 Видео
11. Прямая в пространстве и ее уравненияСкачать

Уравнение прямой в пространстве. 11 класс.Скачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Видеоурок "Общие уравнения прямой"Скачать

Уравнение прямой по рисунку. #математика #уравнение #прямая #алгебра #наклон #точка #simplemathСкачать

Лекция 28. Виды уравнения прямой в пространстве.Скачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Геометрия. 9 класс. Уравнение прямой. Направляющий вектор и вектор нормали прямой /22.10.2020/Скачать

УРАВНЕНИЕ ПРЯМОЙСкачать
Параметрические уравнения прямойСкачать









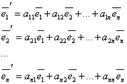


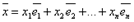

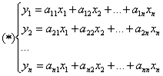





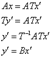
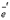




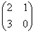


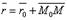


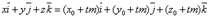

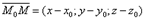

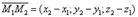




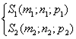


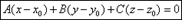


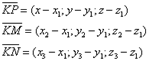




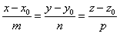

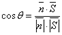

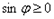



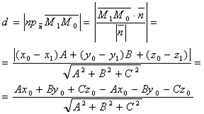
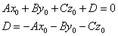




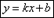
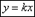
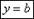








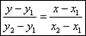







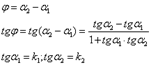

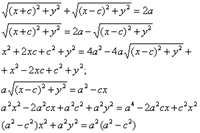










































 .
. и
и  .
. ,
,  .
. , такая, что Р и С лежат в одной плоскости.
, такая, что Р и С лежат в одной плоскости. ,
,