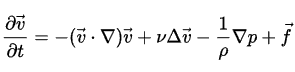Уравнения ньютона для вязкости газов

Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Основные законы движения жидкостей и газов

Для расчета движения воды в трубопроводе нужно знать не так уж и много. Для этого не надо глубоко изучать физику, но всё же некоторое основные понятия изучить придется.

В этой статье я приведу самые основные формулы, которые вам пригодятся не только для расчетов, но и для общего понимания, что может влиять в вашем водопроводе на его течение. Иногда общее понимание процессов поможет вам избежать ошибок при монтаже системы.

Например, не все знают, что в части водопровода с трубами меньшего диаметра давление на стенки меньше, чем на участке с трубами большего диаметра. Почему возникает кавитация и вообще, что это такое. А это надо знать.

Статья будет обновляться и дополняться.

Видео:Вязкость и течение Пуазёйля (видео 14) | Жидкости | ФизикаСкачать

Уравнение неразрывности

Для жидкости, текущей в трубе, этот закон используют в такой форме (называемой уравнением неразрывности):

Где v — скорость жидкости S — площадь сечения трубы, по которой течёт жидкость. Сформулировать этот закон можно и так:

Сколько вливается жидкости в ёмкость, в данном случае в трубу, столько должно и выливаться, если условия течения не изменяются.

Скорость в узких участках трубы должна быть выше, чем в широких.

Видео:Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Уравнение Бернулли стационарного движения

Одно из важнейших уравнений гидромеханики было получено в 1738 г. швейцарским учёным Даниилом Бернулли (1700 — 1782). Ему впервые удалось описать движение идеальной жидкости, выраженной в формуле Бернулли.

Идеальная жидкость — жидкость, в которой отсутствуют силы трения между элементами идеальной жидкости, а также между идеальной жидкостью и стенками сосуда.

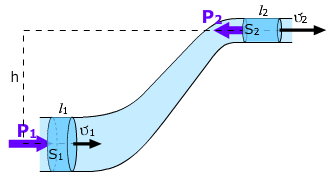
Уравнение стационарного движения, носящее его имя, имеет вид:

где P — давление жидкости, ρ − её плотность, v — скорость движения, g — ускорение свободного падения, h — высота, на которой находится элемент жидкости.

Смысл уравнения Бернулли в том, что внутри системы заполненной жидкостью (участка трубопровода) общая энергия каждой точками всегда неизменна.

В уравнении Бернулли есть три слагаемых:

• ρ⋅v 2 /2 — динамическое давление — кинетическая энергия единицы объёма движущей жидкости;
• ρ⋅g⋅h — весовое давление — потенциальная энергия единицы объёма жидкости;
• P — статическое давление, по своему происхождению является работой сил давления и не представляет собой запаса какого-либо специального вида энергии («энергии давления»).

Это уравнение объясняет почему в узких участках трубы растёт скорость потока и падает давление на стенки трубы. Максимальное давление в трубах устанавливается именно в месте, где труба имеет наибольшее сечение. Узкие части трубы в этом отношении безопасны, но в них давление может упасть настолько, что жидкость закипит, что может привести к кавитации и разрушению материала трубы.

Видео:Урок 137. Движение тела в жидкости и газе.Скачать

Явление кавитации

Кавитация (от латинского cavitas — «углубление», «полость») — процесс образования полостей (пузырьков) в движущейся жидкости вследствие понижения давления.

Явление кавитации также объясняется уравнением Бернулли. Если скорость течения жидкости значительно возрастает, то давление сильно понизится — настолько, что жидкость закипит. Такую скорость можно получить, если пропускать жидкость через очень узкий участок трубы или при быстром обращении лопатки в водяном насосе.

Пузырьки по ходу движения жидкости попадают в области жидкости с нормальным давлением и там схлопываются. Это схлопывание сопровождается гидродинамическими эффектами, способными привести к разрушению трубы или стенок насоса.

Видео:Движение тел в жидкостях и газах. Лобовое сопротивление и подъемная сила. Формула Стокса. 10 класс.Скачать

Гидродинамика Эйлера и Навье-Стокса

Уравнение Бернулли позволяет объяснить очень много интересных гидродинамических явлений, но гораздо больше явлений, происходящих в движущихся жидкостях и газах, с его помощью объяснить нельзя, потому что этот закон для идеальной жидкости, т.е для жидкости, которая не обладает внутренним трением, а значит не создает гидравлическое сопротивление..

Реальная жидкость отличается от идеальной и обладает внутренним трением, или по другому называют вязкостью. Два соприкасающиеся элемента жидкости, двигающиеся в одном и том же направлении, но с разными скоростями, воздействуют друг на друга. Сила взаимодействия ускоряет медленно движущийся элемент жидкости и замедляет более быстрый.

Видео:Определение коэффициента вязкости жидкости. Проверка закона СтоксаСкачать

Закон вязкого трения Ньютона

Ньютон предположил, что величина этой силы (называемой силой внутреннего трения) пропорциональна разности скоростей элементов жидкости. Следовательно, сила внутреннего трения F пропорциональна изменению скорости жидкости v в направлении, перпендикулярном движению, и зависит от площади S соприкосновения элементов жидкости:

η − коэффициент динамической вязкости.

Жидкости, в которых внутреннее трение подобным образом зависит от изменения скорости, называются ньютоновскими, или жидкостями с линейной вязкостью.

Величину коэффициента динамической вязкости (и справедливость данного закона) Ньютон определил с помощью несложного опыта: он передвигал по поверхности жидкости пластинку с той или иной скоростью. Для того чтобы поддерживать эту скорость постоянной, требовалась сила, которая при небольшой глубине жидкости оказалась прямо пропорциональна площади S и скорости пластинки v и обратно пропорциональна глубине жидкости h:

И хотя при увеличении глубины жидкости h сила вязкого трения пластинки не становится исчезающе малой, эта формула довольно точно описывает взаимодействие между соприкасающимися элементами жидкости.

Чем больше разность скоростей, тем больше сила, с которой они воздействуют друг на друга, заставляя притормаживать слишком быстро движущиеся элементы и разгоняя слишком медленные.

В результате относительное движение в жидкости прекращается (но иногда это может произойти не очень скоро).

Видео:Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Уравнение Навье — Стокса для вязких жидкостей

В более строгой формулировке линейная зависимость вязкого трения от изменения скорости движения жидкости называется уравнением Навье — Стокса. Оно учитывает сжимаемость жидкостей и газов и, в отличие от закона Ньютона, справедливо не только вблизи поверхности твёрдого тела, но и в каждой точке жидкости (у поверхности твёрдого тела в случае несжимаемой жидкости уравнение Навье — Стокса и закон Ньютона совпадают).

Любые газы, для которых выполняется условие сплошной среды, подчиняются и уравнению Навье — Стокса, т.е. являются ньютоновскими жидкостями.

Вязкость жидкости и газа обычно существенна при относительно малых скоростях, потому иногда говорят, что гидродинамика Эйлера — это частный (предельный) случай больших скоростей гидродинамики Навье — Стокса.

При малых скоростях в соответствии с законом вязкого трения Ньютона сила сопротивления тела пропорциональна скорости. При больших скоростях, когда вязкость перестаёт играть существенную роль, сопротивление тела пропорционально квадрату скорости (что впервые обнаружил и обосновал Ньютон).

Видео:Вязкость газов.Скачать

Критерий Рейнольдса

Такую зависимость вывел английский физик и инженер Осборн Рейнольдс (1842 — 1912).

Критерий, который помогает ответить на вопрос, есть ли необходимость учитывать вязкость, является число Рейнольдса Re. Оно равно отношению энергии движения элемента текущей жидкости к работе сил внутреннего трения.

Рассмотрим кубический элемент жидкости с длиной ребра n. Кинетическая энергия элемента равна:

Согласно закону Ньютона, сила трения, действующая на элемент жидкости, определяется так:

Работа этой силы при перемещении элемента жидкости на расстояние n составляет

а отношение кинетической энергии элемента жидкости к работе силы трения равно

Сокращаем и получаем:

Re — называется числом Рейнольдса.

Таким образом, Re — это безразмерная величина, которая характеризует относительную роль сил вязкости.

Например, если размеры тела, с которым соприкасаются жидкость или газ, очень малы, то даже при небольшой вязкости Re будет незначительно и силы трения играют преобладающую роль. Наоборот, если размеры тела и скорость велики, то Re >> 1 и даже большая вязкость почти не будет влиять на характер движения.

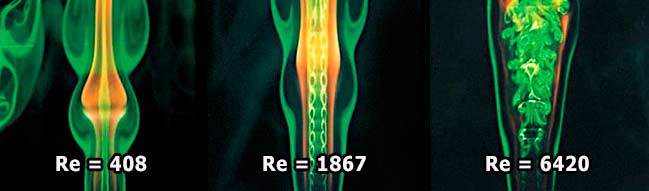
Однако не всегда большие числа Рейнольдса означают, что вязкость не играет никакой роли. Так, при достижении очень большого (несколько десятков или сотен тысяч) значения числа Re плавное ламинарное (от латинского lamina — «пластинка») течение превращается в турбулентное (от латинского turbulentus — «бурный», «беспорядочный»), сопровождающееся хаотическими, нестационарными движениями жидкости. Этот эффект можно наблюдать, если постепенно открывать водопроводный кран: тонкая струйка течёт обычно плавно, но с увеличением скорости воды плавность течения нарушается. В струе, вытекающей под большим напором, частицы жидкости перемещаются беспорядочно, колеблясь, всё движение сопровождается сильным перемешиванием.

Появление турбулентности весьма существенно увеличивает лобовое сопротивление. В трубопроводе скорость турбулентного потока меньше скорости ламинарного потока при одинаковых перепадах давления. Но не всегда турбулентность плоха. В силу того что перемешивание при турбулентности очень значительно, теплообмен — охлаждение или нагревание агрегатов — происходит существенно интенсивнее; быстрее идёт распространение химических реакций.

Формула Бернулли закон по которому течет жидкость на любом отрезке трубы, что значительно помогает при проектировании трубопроводов, особенно с естественной циркуляцией.

Все материалы, представленные на сайте, носят исключительно справочный и ознакомительный характер и не могут считаться прямой инструкцией к применению. Каждая ситуация является индивидуальной и требует своих расчетов, после которых нужно выбирать нужные технологии.

Не принимайте необдуманных решений. Имейте ввиду, что то что сработало у других, в ваших условиях может не сработать.

Администрация сайта и авторы статей не несут ответственности за любые убытки и последствия, которые могут возникнуть при использовании материалов сайта.

Сайт может содержать контент, запрещенный для просмотра лицам до 18 лет.

Видео:Урок 134. Применения уравнения Бернулли (ч.1)Скачать

Вязкость (внутреннее трение). Закон Ньютона. Коэффициент вязкости

Вязкость (внутреннее трение) связано с возникновением сил трения между слоями газа (жидкости), перемешивающимися друг с другом с различными по модулю скоростями.

Со стороны слоя движущегося быстрее, на более медленно движущийся слой действует ускоряющая сила и наоборот, медленно перемещающийся слой тормозит более быстро движущиеся слои газа (жидкости). Силы трения которые при этом возникают, направлены по касательной к поверхности соприкосновения слоев. С молекулярно-кинетической точки зрения причиной вязкости является упорядоченное движение слоев с различными скоростями u и хаотичного движения молекул υ.

Согласно закону Ньютона сила трения между двумя слоями газа или жидкости равна.

Эмпирическое уравнение вязкости, закон Ньютона:

где η – коэффициент вязкости; — величина показывающая, как быстро изменяется

скорость течения жидкости или газа в направлении z, перпендикулярном к направлению движения слоев (градиент скорости u), S – площадь лежащей на границе между слоями поверхности, по которой действует сила F.

Согласно 2-му закону Ньютона:

или, , тогда

Уравнение Ньютона для внутреннего трения можно представить в виде:

где Δр_им – импульс, передаваемый от слоя к слою за секунду (Δt=1 с), т.е. поток импульса через поверхность S. Знак «минус» в формуле обусловлен тем, что импульс «течет» в направлении убывания скорости u. Поэтому знаки импульса и градиента скорости u противоположны.

В формуле Ньютона минус писать нельзя, потому что она определяет одинаковый модуль двух противоположно направленных сил, с которыми слои действуют друг на друга. Кроме того нужно брать модуль градиента скорости, так как производная может иметь любой знак, а модуль силы – положительная величина.

Рассмотрим происхождение силы внутреннего трения.

Рассмотрим два соприкасающихся слоя газа толщиной Δz. Слои движутся с различными скоростями u₁ и u₂. Каждая молекула газа участвует в двух движениях: хаотическом тепловом, средняя скорость которого равна , и упорядоченном движении со скоростью потока u. Скорость потока намного меньше, чем скорость теплового движения. В неподвижном газе средний импульс молекулы равен нулю. Молекула в потоке газа обладает средним импульсом mu. При рассмотрении внутреннего трениянас будет интересовать этот импульс.

Пусть в некоторый момент времени слои обладают импульсами р_им1 и р_им2. При отсутствии внешнего воздействия на слои, их импульсы не могут оставаться неизменными, так как вследствие теплового движения происходит непрерывный переход молекул из одного слоя в другой. Попав в другой слой, молекула претерпевает столкновения с молекулами этого слоя, в результате чего она отдает избыток своего импульса другим молекулам ( если она прилетела из слоя, движущегося быстрее), либо увеличивает свой импульс за счет других молекул (если она прилетела из слоя, движущегося медленнее). В итоге импульс слоя, движущегося быстрее, убывает, а слоя, движущегося медленнее, возрастает. Следовательно, слои ведут себя так, как если бы к слою, скорость которого больше, была приложена сила, тормозящая его движение, а к слою, скорость которого меньшая, — такая же по модулю сила, ускоряющая его движение. Таков механизм возникновения сил внутреннего трения.

Через поверхность S, лежащую на границе раздела слоев, переходит в единицу времени из одного слоя в другой количество молекул, определяемое выражением:

на среднюю скорость молекул в направлении, перпендикулярном к слоям, движение слоев со скоростью u не оказывает влияния). В результате возникает в направлении от более быстрого слоя к более медленному поток импульса через поверхность S, равный:

В реальном потоке газа скорость при переходе через воображаемую границу двух слоев изменяется не скачком, а непрерывно по закону u=u(z). Будем считать, что каждая молекула, пролетающая через поверхность S, несет с собой импульс mu, определяемый скоростью u в том месте, где произошло столкновение молекулы. Это столкновение происходит на различных расстояниях от S. В среднем последнее столкновение происходит на расстоянии, равном длине свободного пробега λ. Поэтому молекулам, летящим в направлении оси z, припишем значение скорости u₁=u(z–λ), а молекулам, летящим в противоположном направлении, – значение скорости u₂=u(z+λ). Подстановка этих значений в формулу для потока импульса через поверхность S в направлении оси z дает выражение:

Произведение nm равно плотности газа ρ. Поэтому полученное уравнение можно записать в виде:

Сравнение полученного уравнения с эмпирической формулой Ньютона дает для вязкости выражение:

Размерность вязкости [η] = 1 (кг/(м∙с)) = 1 (Па∙с).

Видео:Алгоритм решения задач на второй закон Ньютона часть 1| Физика TutorOnlineСкачать

Основные понятия

Вязкость (внутреннее трение) — одно из трёх явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.

Различают динамическую вязкость(первая) [еденици измерения: пуаз, Па*с], вторая, вязкость жидкостей, вязкость полимера, разряжённых газов, и кинематическую вязкость [единицы измерения: стокс, м²/с, внесистемная единица — градус Энглера].Вторая вязкость (оэффециент второй вязкости) ζ, подобно динамической (первой) вязкости η, является положительной величиной и зависит от химической природы вещества, давления и температуры. Вязкость в жидкостях подчиняется тем же дифференциальным уравнениям, что и соответствующие явления в газах. Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества и своим происхождением обязана классическим методам измерения вязкости, таким как измерение времени вытекания заданного объема через калиброванное отверстие под действием силы тяжести. Вязкость полимерных растворах характеризуется следующими величинами: относительной вязкостью, или вязкостным отношением. Внутреннее трение разряжённых газовотсутствует и существует лишь внешнее трние движущегося газа. Прибор для измерения вязкости называется вискозиметром.

Ньютоновскими называют жидкости, для которых вязкость не зависит от скорости деформации. Если вязкость падает при увеличении скорости, жидкость называется тиксотропной. Для неньютоновских жидкостей методика измерения вязкости получает первостепенное значение.

Вязкость газов (внутреннее трение)

Явление внутреннего трения (вязкости) связано с возникновением сил трения между двумя слоями газа перемещающимся паралельно друг другу с различными по величине скоростями. Причинной внутреннего трения является перенос молекулами количества движения из одного слоя газа в другой, тоесть выравниваются скорости движения различных слоёв газа.

По этому свойству мы обязаны, например, тем, что ветер или буря с течением времени утихают. Выравнивание скоростей, соседних слоёв газа, если эти скорости различны, происходит потому, что из слоя газа с большей скоростью движения переносится импульс к слою, движущемуся с меньшей скоростью.

Если внешними силами поддерживается постоянной разность скоростей движения различных слоёв газа, то и поток импульса от слоя к слою будет постоянным, причём этот поток будет направлен вдоль падения скорости. С таким случаем мы, например, встречаемся при медленном течении газа (или жидкости) между двумя пластинами или в трубе под действием постоянной внешней разности давлений, направленной вдоль движения.

Известно, что при течение газа вдоль трубы скорости разных слоёв распределены так, как это показано на рисунке (б) где стрелки представляют векторы скорости движения газа. Наибольшая скорость наблюдается в средней, прилегающей к оси части трубы; по мере приближения к стенкам скорость уменьшается, а слой прилегающий непосредственно к стенкам трубы, покоится.

При таком течении происходит перенос импульса от центрального слоя газа, где скорость наибольшая, к слоям, движущимся с меньшей скоростью. Так как этот процесс связан с изменением количества движения, то газ ведёт себя так, как если бы на него действовала некоторая сила (сила внутреннего трения).

Количественно перенос импульса может быть описан так же, как мы описали перенос энергии в процессе теплопроводности. Пусть изменение скорости движения газа происходит в направлении оси Х, которое в данном случае перпендикулярно к направлению самой скорости движения газа (см. рисунок)

В направлении, перпендикуляр-ном к оси Х, скорость движения во всех точках одинакова. Это значит, что скорость υ является функцией только х. Тогда, как показывает опыт, количество движения L, переносимое за 1 с. через 1 сечения, перпендикулярного оси Х, определяется уравнением.

L=-η (1)

Где dν/dx — градиент скорости вдоль оси Х, характеризующий быстроту изменения скорости вдоль этой оси (изменение скорости на каждую единицу длинны). Знак минус означает, что импульс переносится в направлении уменьшения скорости.

Коэффициент η называется коэффициентом вязкости или коэффициентом внутреннего трения газа и так же, как коэффициенты диффузии и теплопроводности, зависит от свойств газа. Иногда коэффициент η, определённый уравнением (1), называют коэффициентом динамической вязкости, в отличие от коэффициента кинематической вязкости, равного отношению η/ρ, где ρ-рлотность газа. Физический смысл коэффициента вязкости заключается в том, в единицу времени (1с.) через площадку в 1 при градиенте скорости (в направлении перпендикулярном к площадке), равном единице (1м/с на 1см длинны). За единицу вязкости в системе единиц СИ принимается коэффициент вязкости такого вещества, в котором при градиенте скорости, равном единице (1 с), через площадку 1 м переносится количество движения 1 кг·м/с за 1с. Значит, коэффициент вязкости измеряется в единицах [кг/м·с]. В системе СГС коэффициент измеряется в единицах [г/см·с]. Эта единица называется пуаз.

При переносе импульса от слоя к слою происходит изменение импульса этих слоёв. Это значит, что на каждый из слоев действует сила, равная изменению импульса в единицу времени (второй закон Ньютона). Ведь L в уравнение (1) –это перенос импульса в единицу времен!! Следовательно, вязкость приводит к тому, что любой слой газа, движущийся относительно соседнего, испытывает действие некоторой силы. Сила это есть ничто иное, как сила трения между слоями газа, движущихся с различными скоростями. Отсюда и название внутреннее трение. Уравнение (1) можно поэтому записать и в виде.

F=-η (1а)

Где F –сила, действующая на единицу площади поверхности, разделяющих два соседних слоя газа. Коэффициент вязкости численно равен силе, действующей на единицу площади при градиенте скорости, равном единице.

Внутреннее трение является причиной того, что для протекания газа (или жидкости) через требуется некоторая разность давлений. Чтобы скорость течения имела некоторое данное значение, эта разность давлений должна быть тем больше, чем больше коэффициент внутреннего трения η.

Зависимость между объемом V протекающего в единицу времени через сечение трубы газа и требуемой для этого разностью давлений Δр устанавливается известной формулой Пуазейля:

V= (2)

Где l –длинна трубы и R –её радиус.

Пользуясь этой формулой, можно, измерив объём газа, протёкшего за некоторый промежуток времени через трубу, разность давлений на её концах и зная геометрические размеры трубы, определить коэффициент вязкости газа.

Вычисление коэффициентов вязкости газов. Если газ течет с некоторой скоростью υ, то значит, что все его молекулы обладают этой скоростью сверх скорости теплового движения, которое в текущем газе происходит совершенно так же, как и покоящемся. Каждая молекула имеет, следовательно, импульс mυ, направленный в одном для всех молекул направлении.

Рассмотрим площадку S, параллельную скорости течения газа и, следовательно, перпендикулярную к направлению переноса импульса (см. рис). Пусть скорость течения газа убывает в направлении оси Х. Благодаря обмену молекулами между обоими слоями газа (обмен происходит из-за движений) это различие уменьшается. Молекулы справа от S замещаются другими молекулами, пришедшими слева, имеющими большую скорость и, следовательно, больший импульс. При столкновении этих молекул с молекулами, находившихся до этого справа от S, большая скорость течения распределиться между всеми молекулами справа, после чего скорость течения этого слоя, а следовательно, и импульс, станут больше, в то время как скорость и импульс слоя газа слева от S уменьшается.

Величина потока импульса L, переносимого в единицу времени (1с.) через единицу площади S, определяется разностью импульсов L и L, переносимых молекулами, пресекающими площадку S слева и справа. Импульс L, переносимый молекулами слева направо, равен произведению импульса отдельной молекулы на число молекул, пересекающих единицу площади в единицу времени. Последнее, как было показано выше, равно nυ (n –число молекул в единице объёма, υ –средняя скорость теплового движения молекулы).

Если скорость течения газа на расстоянии λ (длинна свободного пробега) слева от S равна υ, то импульс молекулы, связанный с течением газа, равен m υ (m –масса молекулы). Таким образом,

L=nυmυ,

соответственно для молекул, пересекающих площадь S справа,

L=nυmυ,

где υ — скорость течения газа на расстоянии λ справа от S. Результирующий поток импульса L через единицу площади за 1 с. равен

L= L-L= nυm(υ— υ),

где υ— υ — разность скоростей течения газов в точках, отстоящих друг от друга на расстоянии 2 λ,

υ— υ= — 2 λ,

L= — nυm λ.

Сравнивая это выражение с (1) получаем выражение для коэффициента вязкости:

η=nυmλ=υλρ, (3)

Выражение (3), так же как и полученное ранее значении коэффициента теплопроводности, даёт оценку коэффициента вязкости с точностью до численного множителя, который только приблизительно равен 1/3. Из этого выражения видно, что коэффициент вязкости тоже не должен зависеть от давления, так как произведение λρ не зависит от давления. Опыты по измерению вязкости в широком диапазоне давлений подтверждают этот вывод.

χ= ηС

Это уравнение устанавливает связь чисто механическими и тепловыми явлениями в газе.

Коэффициент внутреннего трения должен, так же как и коэффициент теплопроводности и удельной теплоёмкости, зависеть от температуры, так как в выражении для η входит средняя скорость тепловых движений молекул, зависящей от температуры по закону . Значит, коэффициент вязкости тоже должен расти с повышением температуры пропорционально . В действительности вязкость растёт несколько быстрее, чем . Это связано с тем, что с повышением температуры не только растёт скорость молекул, но и уменьшается эффективное поперечное сечение молекул и потому растёт длинна свободного пробега; расстояние от места последнего перед данным слоем столкновения становятся большим, и, следовательно, увеличивается изменение импульса, которое молекула с собой принесёт. Так как в выражение для η входит средняя длинна свободного пробега, то изменение коэффициента вязкости, так же как и теплопроводности, позволяет определить (или, по крайней мере оценить) размер молекулы.

Измерение коэффициента вязкости (вискозометрия). Как уже упоминалось, коэффициент вязкости можно определить, если измерять скорость течения газа через трубу известных геометрических размеров. Пользуясь формулой Пуазейля (2), из таких измерений можно вычислить коэффициент вязкости. Следует, однако, иметь ввиду, что для такого опыта пригодна не всякая труба. Дело в том, что для измерения вязкости необходимо, чтобы течение газа было ламинарным. Этим термином обозначается такое течение газа (или жидкости), при котором скорость движения газа в направлении, перпендикулярном к оси трубы, во всех точках равна нулю, то есть при котором слои газа текут хотя и с различными скоростями, но параллельно друг к другу. Между тем при определённом значении скорости течения, зависящих от свойств газа и от радиуса трубы, в газе начинаются появляться вихри, нарушающие ламинарность течения. Для такого вихревого, или турбулентного, течения формула Пуазейля не справедлива. Чем меньше сечение трубы, тем большая скорость требуется для появления вихрей. Поэтому метод измерения вязкости, основанный на использовании формулы Пуазейля, часто называют методом капилляра, а соответствующие приборы –капиллярными вискозиметрами.

Из механики газов и жидкостей известно, что переход от ламинарного к вихревому (турбулентному) движению происходят не скачком, но при вполне определённых условиях, связанных со свойствами газа (жидкости), с размерами трубы и скоростью движения. Так, для течения в цилиндрической трубе переход к турбулентному движению происходит, когда безразмерная величина ur

Re=

становится больше некоторого критического значения, порядка 1000. Здесь ρ –плотность газа, u –средняя скорость течения, r –радиус трубы и η –вязкость газа. Называется эта величина числом Рейнольдса. Если число Рейнольдса меньше критического значения –движение ламинарное, если превышает –турбулентное.

Число Рейнольдса, характеризует соотношение между инерционными и вязкостными силами, действующими в движущейся жидкости или газе. Оно имеет, однако, и простой молекулярно-кинетический смысл. Подставив в выражение для Re вместо η его значение из (3) получим:

Re≈.

Значит, для того, чтобы течение газа стало турбулентным, нужно, чибо чтобы скорость течения газа была велика по сравнению со средней скоростью тепловых движений молекул, либо радиус трубы должен быть большим по сравнению с длинной свободного пробега. Очевидно, чтобы движение было ламинарным, скорость движения газа u должна быть небольшой. Только в этом случае Re может быть меньше критического значения (порядка 1000)

Метод затухания колебаний. Для измерения коэффициента вязкости не требуется, чтобы непрерывно газ двигался относительно покоящихся стенок сосуда. Можно использовать и движение твёрдой стенки относительно газа. Так именно обстоит дело в вискозиметрах, в которых коэффициент вязкости определяется по затуханию колебаний диска, среды или цилиндра, подвешенных в исследуемом газе и совершающих колебания в нём.

Измерение вязкости сводится к тому, что, вызвав внешним магнитом крутильные колебания диска, измеряют (по отражению в зеркальце освещённой шкалы) амплитуды следующих одно за другим колебаний, а так же время одного полного колебания (оно от амплитуде практически не зависит). Из этих данных можно вычислить коэффициент вязкости по следующей формуле:

η=

Здесь κ –логарифмический декремент затухания диска, κ-логарифмический декремент затухания подвеса без диска, τ –время одного полного колебания и с –константа, зависящая от свойств прибора, которая должна быть однажды определена. Проще всего это сделать, измерив на вискозиметре вязкость уже исследованного газа. Описанный прибор пригоден для измерения вязкости при низких температурах и при низких давлениях.

Вязкость в жидкостях

Внутреннее трение (вязкость) жидкостей, как и газов, возникает при движении жидкости из-за переноса импульса в направлении, перпендикулярном к направлению движения. Перенос импульса из одного слоя в другой осуществляется при скачках молекул, о которых говорилось ранее. Общий закон внутреннего трения –это закон Ньютона. Коэффициент же вязкости η может быть получен на основе тех же соображений о движениях молекул, которые мы уже приводили. Очевидно, что жидкость будет тем более текучей ( с тем меньшей вязкостью), чем меньше время t «оседлости» молекул и значит чем чаще происходят скачки. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля –Андраде:

η=Се

множитель С, входящий в это уравнение, зависит от дальности скачка δ, частоты колебаний ν и температуры. Однако температурный ход вязкости определяется множителем е. Как следует из этой формулы, с повышением температуры вязкость быстро уменьшается. Так, вязкость воды при изменении температуры от 0С до 100С уменьшается от 1,8·10 до 2,8·10 кг/м·с. О численных зачениях коэффициента вязкости жидкостей при комнатной температуре можно судить по данным таблицы.

Коэффициент вязкости некоторых жидкостей

Ньютоновская и неньютоновская жидкости

Вязкие тела отличаются от пластичных тем, что текут при любых напряжениях (τ=0). Течение идеально вязких тел (жидкостей) описывается известным законом Ньютона, который в случае сдвига выражается в следующей форме:

= τ =η, (1)

где f –сила вязкостного сопротивления; η –динамическая вязкость. Закн Ньютона является определением понятия η:

η= (2)

Понятия «жидкости» и «твёрдый» материал не являются абсолютными и связаны со скоростью деформации. Тем не менее многие структурированные системы низким содержанием дисперсной фазы, характеризующиеся малой прочностью, обладают текучестью, близкой к течению чистых жидкостей. Для изучения особенностей течения подобных систем, как и неструктурированных суспензий и золей, применяют обычный для жидкостей метод капиллярной вискозиметрии, основанный на измерении объёмной скорости течения через капилляр.

Применение закона Ньютона к ламинарному течению в цилиндрическом капилляре или трубке, характеризуемому условием Re τ структурную сетку можно рассматривать как сплошной статический твёрдообразный упругий каркас (матрицу).

Далее с ростом τ начинается постепенное разрушение временных контактов между элементами структуры и и образование других: возникает динамическое равновесие, резко возрастает, и для многих пластичных тел реологическая кривая выходит на линейный участок ВС, отражающий нарастающее разрушение структуры. Изучение реологических свойств пластичных тел было впервые проведено выдающимся русским учёным Шведовым (1889г.); закон течения в области разрушения структуры для этих тел (участок ВС)описывается уравнением Шведова –Бингама:

τ= τ+η*· . (6)

Величина τ (находимая путём экстраполяции прямой ВС на ось τ) называется предельным динамическим напряжением сдвига и характеризует сдвиговую прочность структуры. Постоянная η* носит название пластической вязкости; она учитывает (через η*· = τ — τ) ту часть сопротивления деформации, которая пропорциональна скорости сдвига. Другая часть сопротивления, не зависящая от , учитывается величиной сдвига прочности τ. Напряжение как бы разбивается на две составляющие: необходимые для разрушения структуры (τ) и осуществляющие течение (τ — τ); однако фактически оба процесса осуществляются во времени. Определение τ посредствам экстраполяции отрезка ВС на ось абсцисс количественно характеризует прочность структуры.

Участок ВС пластического течения, характеризующий равновесное состояние разрушения и восстановления структуры, может быть описан так же уравнением Ньютона (1) с переменной вязкостью. Из (1) и (6) следует:

η=η*+= η* (7)

Из (7) видно, что с ростом τ значение η уменьшается и в пределе при τ>> τ стремится к η*; кривая течения должна выходить на прямую для ньютоновской жидкости с полностью разрушенной структурой; однако практически ещё до полного разрушения течение становится турбулентным, и все закономерности, установленные для ламинарного течения, нарушаются.

Значения η при течении могут изменяться на несколько порядков от η, отвечающего полностью не разрушенной структуре, до η*, характерного для предельно разрушенной структуры. Так, для суспензий бентонитовых глин η≈10, η*≈10П. Следует отметить, что кривые течения могут иметь иной вид; так, для концентрированных систем, содержащих >30% дисперсной фазы в виде мелких твёрдых частиц, наблюдается иногда не уменьшение, а возрастание вязкости с ростом Р. Это явление, открытое Рейнольдсом (1885 г.), получило название дилатансии.Неньютоновское поведение жидкостей может иметь различные причины: в жидких дисперсных системах определяющую роль играет ориентация частиц дисперсной фазы, изменение их формы и степени агрегации, в коллоидных жидкостях-постепенно углубляющееся с ростом напряжений разрушение (или изменение) внутренней структуры; в полимерах-эффекты механической релаксации. В конкретных случаях может иметь место наложение различных механизмов; напр., неньютоновское поведение наполненных полимеров связано как со структурными перестройками, так и с релаксационными явлениями.

Для множества неньютоновских жидкостей характерны такие явления, как тиксотропия — обратимое уменьшение вязкости («разжижение») жидкости или структурир системы во времени, и дилатансия-рост вязкости предельно наполненных дисперсных систем с вязкой дисперсионной средой. Частный случай неньютоновского поведения жидкости-изменение вязкости с течением времени из-за протекающих в среде химических реакций. Если реакция идет в гомог. среде, изменение вязкости среды отражает изменение ее состава; при этом деформирование обычно не влияет на кинетические закономерности реакции. Однако для гетерог. реакций, например гетерог. полимеризации или отверждения олигомеров, деформирование (например, сдвиговое течение в реакторе или воздействие ультразвуковыми колебаниями) влияет на кинетику реакции.

Существование сплошного стационарного каркаса, обладающего упругостью, при τ ≤ τ>0 позволяет считать системы твёрдообразнвми, несмотря на то, что они могут, например, подобно жидкостям вытекатьиз наклонённого сосуда под действием силы тяжести (τ > τ). Таковы растворы желатины при с≥1%, если значения рН удалены от ИЭТ; они обнаруживают непрерывный переход от жидкости (τ=0; τ>0) к твёрдообразным (τ> τ>0) структкрам при увеличении концентрации желатины или уменьшении температуры. С ростом концентрации дисперсной фазы τувеличивается, образуется гель.

Примером неньютоновской жидкости является вода, смешанная с обыкновенной мукой. При должной концентрации муки это вещество будет повышать вязкость под действием удара так что человек может совершенно спокойно пробежаться по поверхности бассейна, наполненного неньютоновской жидкостью – она просто затвердевает под ногами бегущего. Но стоит экспериментатору на мгновение остановиться, как он сразу начнет тонуть. Инструкция по созданию подобной жидкости в домашних условиях довольно проста, а особенно интересные эффекты можно получить, поместив емкость с такой необыкновенной жидкостью на обыкновенный акустический динамик.

Ферромагнитные жидкости состоят из ферромагнитных частиц нанометровых размеров, находящихся во взвешенном состоянии в несущей жидкости, в качестве которой обычно выступает органический растворитель или вода. Для обеспечения устойчивости такой жидкости ферромагнитные наночастицы связываются с поверхностно-активным веществом, образующим защитную оболочку вокруг частицы и препятствующем их слиянию (из-за Ван-дер-Вальсоаских или магнитных сил).

Несмотря на название, ферромагнитные жидкости не проявляют ферромагнитных свойств, поскольку не сохраняют остаточной намагниченности после исчезновения внешнего магнитного поля. На самом деле ферромагнитные жидкости являются парамагнетиками и их часто называют «суперпарамагнетиками» из-за высокой магнитной восприимчивости. Действительно ферромагнитные жидкости в настоящее время создать сложно

ПУЗЫРЬ, ПОДНИМАЮЩИЙСЯ В НЬЮТОНОВСКОЙ И НЕНЬЮТОНОВСКОЙ ЖИДКОСТЯХ

1) Курс Коллоидной химии. для высшей школы; Санкт-Петербург «химия» 1995

2) и Справочник по Физике (для инженеров и сотрудников вузов); Издательство «НАУКА»; Москва 1965 г.

3) Курс общей физики, книга 3 молекулярная физика и термодинамика; Москва «НАУКА» 1998 г.

4) , Молекулярная физика; Издательство «НАУКА» Главная редакция Физико-Математической литературы Москва 1976 г.

5) Н. Б Урьев Физико-химические основы технологии дисперсных систем и материалов, Москва 1988 г.

💡 Видео

Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Три закона НьютонаСкачать

Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Измерение вязкостиСкачать

Газовые законы. Изопроцессы | Физика 10 класс #34 | ИнфоурокСкачать

7.1.5 Уравнения движения жидкости Эйлера и Навье-Стокса. Осреднение для турбулентного течения (RANS)Скачать

ЭТО ОБЯЗАТЕЛЬНО НУЖНО ЗНАТЬ — Второй Закон Ньютона или от чего зависит ускорение телаСкачать

Закон БернуллиСкачать

Физические основы гемодинамики. Определение вязкости жидкостей с помощью вискозиметра.Скачать

Урок 51. Первый закон Ньютона. Взаимодействие тел и их ускорение.Скачать