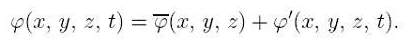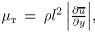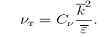Обычно принимается, что УНС достаточно хорошо описывают течения плотных «ньютоновских» газов и жидкостей, как ламинарные, так и турбулентные. Это будет верно в случае, когда масштаб мельчайшей структуры потока, все еще достаточен для справедливости гипотез о сплошности, ЛТР и «законов» Ньютона и Фурье.
Как следствие, можно считать УНС основой для построения моделей всех, в т. ч. турбулентных, течений. Течения можно пытаться моделировать (рассчитывать на ЭВМ) непосредственно по у. Н.-С, для чего
Видео:Уравнения Навье-Стокса - Numberphile на русском.Скачать
требуются размеры расчетных ячеек и величины шагов по времени для адекватного разрешения на сетке наиболее мелкомасштабной вихревой структуры (масштаб Колмогорова).Можно трактовать это как
практическое условие аппроксимации на сетке самих УНС. При невозможности проведения такого расчета остается возможность расчета крупномасштабных вихревых структур с моделированием влияния на этот «основной поток» мелкомасштабных турбулентных вихрей. Крупные вихри при этом по-прежнему могут быть выделены явно на расчетной сетке . Наконец, можно рассчитывать осредненное поле турбулентного течения, приближенно описывая турбулентный перенос моделями турбулентности, на этот раз для всего диапазона ее масштабов.
Во всех случаях, заметим, в основе моделирования лежат УНС
26.Методология расчета осредненного турбулентного течения. Осреднение уравнений Навье-Стокса по Рейнольдсу и по Фавру.
Видео:Science show. Выпуск 51. Уравнение Навье - СтоксаСкачать
Будем различать турбулентные течения статистически стационарные и статистически нестационарные. В первом случае ГУ в среднем (статистически) неизменны по времени, тогда к любому параметру
в любой точке области потока r можно с успехом применить осреднение по времени t, выбрав для этого достаточно большой временной интервал Δt — по следующему простому соотношению
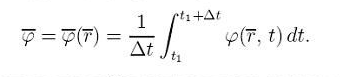
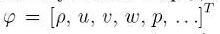
(63)
Поля осредненных величин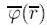 
для статистически стационарного турбулентного течения оказываются гладкими.
При данном подходе моделирование турбулентного течения сводится к расчету рассчитать именно среднестатистическое поле течения.
Модель для расчета осредненного течения получают, подвергая операции осреднения сами у. Н.-С. Осредненные таким способом у. Н.-С. называют уравнениями Рейнолъдса. Так, актуальное (действительное) турбулентное течение может быть представлено в виде суммы осредненной и пулътционной составляющих: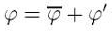 
т. е. 
Представляя искомые функции в у. Н.-С.в виде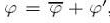 
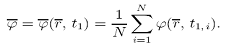
, приводят уравнений к виду, описывающему осредненное течение
Осредненные у. Н.-С. содержат производные по времени и могут использоваться для описания статистически нестационарных течений. Однако в этом случае неявно принимается, что результатом расчета по ним будет картина течения, осредненного не по времени , а по множеству независимых реализаций, т. е. подразумевается осреднение «по ансамблю»
Для течений с ρ=var применяют осреднение по Фавру, т. е. осреднение с использованием плотности в качестве весовой функции. При этом, для плотности используется простое осреднение (63)
а все прочие параметры потока — 
осредняются по Фавру
Вид осредненных но Фавру «сжимаемых» уравнений и дополнительных членов, появляющихся в них при осреднении получается аналогичным виду при простом осреднении течений с р = const.
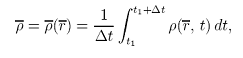
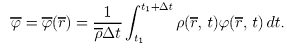
Видео:Уравнение Навье-Стокса на пальцах. МЛФ#2Скачать
Описанная методология именуется в англоязычной литературе как RANS
27. Модели замыкания для расчетов осредненных турбулентных течений: модель пути смешения Л. Прандтля, (к— ε)-модель турбулентной вязкости Классическим представлением о турбулентном переносе является «модель», которая была предложена Л. Прандтлем. В основе ее -модельное представление о турбулентном моле со среднестатистическими характеристиками, который преодолевает расстояние l и затем быстро теряет индивидуальность исчезает, или «диссипирует».
Рассмотрим простейшее плоское сдвиговое течение. По гипотезе Буссинеска превалирующее напряжение Рейнольдса выражается как
Но если выразить в нем, то это (касательное) напряжение запишется более наглядно как:
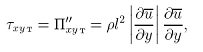
при этом задача «моделирования»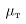 
сводится к заданию зависимости более наглядного параметра- l например, в функции координат точки 
или через обобщенные координаты
Очевидно, что «модель пути перемешивании» не добавляет ничего существенного к определению 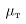, полагаясь на эмпирические данные по l с тем, чтобы расчетное поле осредненного течение близко соответствовало экспериментальным данным. Проблемой этой является не универсальность, когда успешно решаются лишь те задачи, для которых есть проверенные данные по l в поле течения
Модель(к— ε). Эта модель считается «классической» среди моделей, использующих уравнении переноса для характеристик турбулентности, по значениям которых в точках потока вычисляется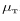 
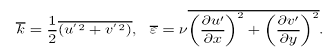
; так достигается большая универсальность в описании течений с различной геометрией. В (к— ε)-модели турбулентной вязкости искомыми в двух дополнительных уравнениях переноса являются осредненные турбулентная кинетическая энергия (ТКЭ) к и скорость диссипации ТКЭ ε. Наиболее простой вид имеет система уравнений с применением (к— ε) модели турбулентности для случая плоского сдвигового течения вдали от стенок в турбулентном потоке несжимаемой жидкости.
Для частного случая ТКЭ и скорость ее диссипации имеют достаточно простое определение
Для вычисления νт по к и ε применяется «связка» Прандтля-Колмогорова, основанная на локальной аналогии с однородной и изотропной турбулентностью: 
28.Методология моделирования крупномасштабных вихрей. «Отфильтрованные» уравнения Навье-Стокса. Если при численном интегрировании уравнений размеры расчетных ячеек не позволяют с достаточной точностью получить все особенности движения, говорят о расчете в приближении модели «крупномасштабных вихрей» (англ. Large Eddy Simulation, LES).
Видео:Вывод уравнений Навье-Стокса - Лекция 3Скачать
При этом для корректности модели па сетке нужна дополнительная модель- для представления не получаемых расчетом на сетке мелкомасштабных движений — «подсеточной» турбулентности. Модель «подсеточного» масштаба позволяет связать влияние мелкомасштабного движения на крупномасштабное. Эффект неизбежного «фильтрования» должен быть учтен априорно и приняты меры по «реконструкции» теряемой информации о мелкомасштабных движениях, т. е. их моделирование.
Моделью течения станут уравнения «отфильтрованные» и замкнутые моделями мелкомасштабных движений. Модифицированная система уравнений сохранит все особенности исходной, но с заменой плотностей потоков молекулярного переноса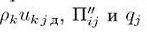 
на их «эффективные» значения.
В методологии LES, в отличие от методологии RANS, приближенно представляется («моделируется») лишь подынтервал наиболее мелких масштабов турбулентного течения. По технологии LES успешно рассчитываются течения весьма общего вида даже при использовании достаточно простых подсеточных моделей.
«Отфильтрованные» уравнения типа уравнений Навье-Стокса. Если же, далее, допустить, что дополнительный «подесточный» турбулентный перенос может быть описан законами, аналогичными законам молекулярного переноса, то эффективные (суммарные) потоки выразятся так:->>>>>>>>>>>>>>>>>>>
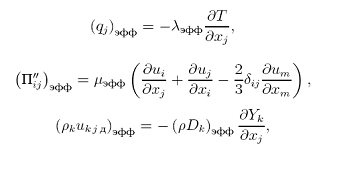
ВИД уравнений «отфильтрованных» уравнении сохранения, справедливых в общем случае для смеси газов:
Аналогичная система уравнений получается в частном случае одного компонента однородной сжимаемой жидкости или газа
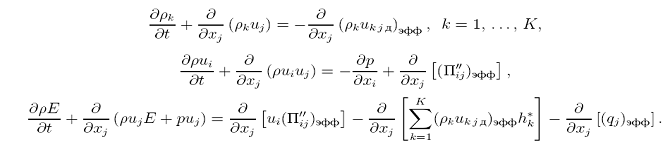
29.Модель подсеточного турбулентного переноса Смагоринского. В простейшем приближении можно считать, что мелкомасштабная «подсеточная турбулентность» еще дополнительно локально изотропна и равновесна. Эти допущения позволяют использовать понятие коэффициента вязкости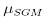 
и прочих обычного вида соотношений для описания переноса импульса, энергии и массы компонентов смеси турбулентностью на «подсеточном» масштабе.
Кроме того, само локальное и текущее значение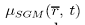 
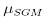
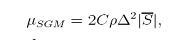
может определяться особенно просто. В самом деле, член обычного вида с «отфильтрованных» уравнениях типа у. Н.-С- обуславливает дополнительную вязкую диссипацию механической энергии крупномасштабного потока в тепловую. При условии локальной равновесности процесса передачи ТКЭ мелкомасштабной турбулентности, «подсеточные» процессы превращают в тепловую столько механической энергии, сколько получают от «надсеточного» движения в каждый момент времени.
Классическая модель Смагоринского получена именно в таком допущении. Согласно этой модели
где Δ— пространственная ширина фильтра, в нашем случае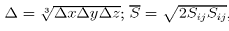 
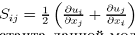
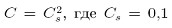
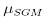
— постоянная Смагоринского, единственная константа данной модели «подесточной турбулентной вязкости». Данная модель дает относительно простую связь коэффициента с размером ячейки применяемой сетки (порядка Δ)
Можно показать, что 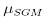по модели (68) становится много меньше μ, когда характерный размер ячейки сетки Δ становится много меньше колмогоровского масштаба, т. е. там и тогда, где «подсеточные» процессы уже не имеют места.
30.Методология моделирования течений непосредственного по уравнениям Навье-Стокса. Пример численного метода для пространственного нестационарного течения. Уравнений Навье – Стокса: это векторное уравнение
Видео:Гладкое решение уравнения Навье — СтоксаСкачать
которое есть уравнение движения (ЗС импульса) для «ньютоновских» жидкостей или газов в приближении μ = const (доказать самостоятельно). Уравнение (6.2) упрощается при ρ = const, тогда div v ≡ 0, и обозначая «кинематический» коэффициент вязкости, получим из (1): (2) Уравнения Навье –Стокса представляют собой систему связанных уравнений в частных производных (УЧП). Аналитическими методами возможно решить небольшое число сравнительно несложных задач. В общем же случае течения, описываемые УНС, должны рассчитываться численными методами на ЭВМ
Намного меньшие вычислительные затраты требуются для расчета по УНС двумерных, чем трехмерных задач, а также задач стационарных, по сравнению с нестационарными.
Уравнения Навье – Стокса, как система и дополненная уравнениями состояния e = e(ρ,T), p =p(ρ,T), μ = μ(ρ, T) и λ= λ(ρ,T), служат основой для описания произвольных — установившихся и нестационарных, ламинарных и турбулентных пространственных течений вязкой по (3.6) («ньютоновской»)
и теплопроводной по (3.15) жидкости. Данные уравнения были получены как следствия законов сохранения в интегральной форме, посредством замыкания указанных соотношений для сплошной среды гипотезами частного вида относительно характера процессов молекулярного переноса
Видео:Уравнение Навье — Стокса для чайниковСкачать
Обобщая модели описывающие взаимодействие потока со скачком сечения в ГВТ, на случай подвода энергии в форме механической работы, можно получить модели, описывающие нестационарное течение через компрессионную или расширительную машину <компрессор или турбину
Обобщение состоит в применении (для «замыкания» задачи) более сложной статической характеристики связующего элемента — уже не вида для МС, а универсальной характеристики компрессора или турбины
Так, для компрессора, в величинами расхода G4, параметров р * 4 и Т * 4, и числа оборотов в минуту ротораnопределяются π * к и η * к, по которым вычисляются
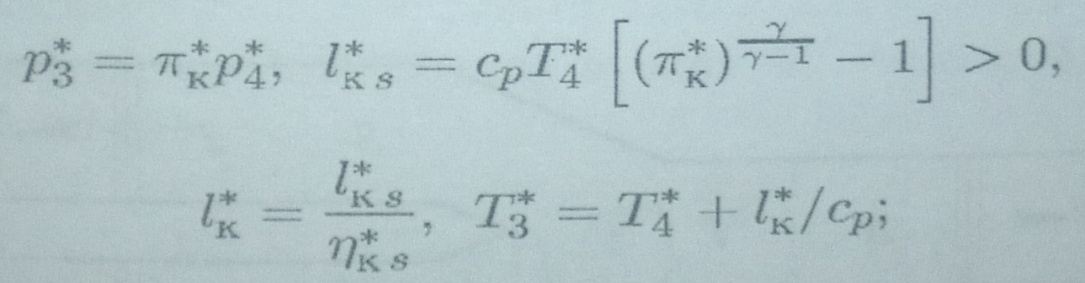
🎥 Видео
Вычислительная гидродинамика (ВГД). Уравнение Рейнольдса и метод конечных объемовСкачать
7.1.5 Уравнения движения жидкости Эйлера и Навье-Стокса. Осреднение для турбулентного течения (RANS)Скачать
Уравнение Рейнольдса-МКМРО3-14-лек-Ахметова А.У.Скачать
1. Определение числа РейнольдсаСкачать
Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать
Вывод уравнения неразрывности - Лекция 1Скачать
Турбулентность на высоких скоростях и число Рейнольдса ( видео 15) | Жидкости | ФизикаСкачать
лекция 7 гидромеханика веснаСкачать
Урок 7.1 (теория) Система дифференциальных уравнений теплообмена и гидродинамикиСкачать
Режимы течения жидкости, ламинарный и турбулентный режимыСкачать
Закон БернуллиСкачать
15-лекция-МКМРО3-Ахметова А.У.-Уравнения рейнольдсовых напряжений.Скачать
Моделирование турбулентности методом крупных вихрей LES в COMSOL MultiphysicsСкачать
Горбачев В. И. - Основы механики сплошных сред. Часть 2 - Течение ПуазейляСкачать
