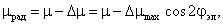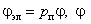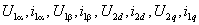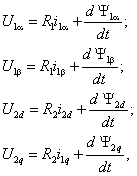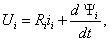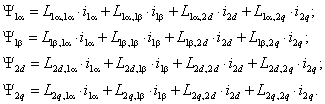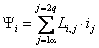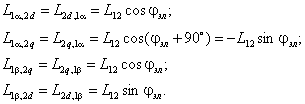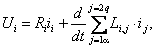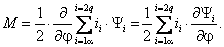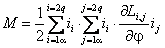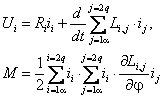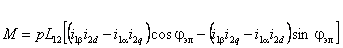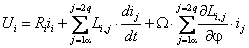Тема: «Краткие сведения из теории обобщенной электрической машины»
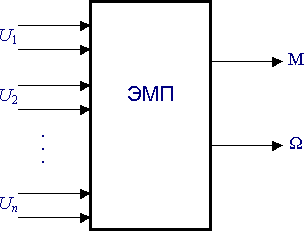
Рассматривая двигатель как элемент электромеханической системы, целесообразно механическую инерцию ротора и момент потерь на его валу отнести к механической части системы, считая механическими переменными электромагнитный момент двигателя М и скорость его ротора 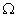
Рис. 2.1. Электромеханический многополюсник
Этому условию соответствует представление двигателя в виде электромеханического многополюсника [2] (рис. 2.1), имеющего пар электрических зажимов, соответствующих обмоткам двигателя, к которым подведены напряжения u1, u2, , un, и одну пару механических зажимов, представляющих безынерционный ротор двигателя, на котором при скорости 
Переменные М, 
Для построения математического описания динамических процессов в электродвигательных устройствах любого типа (постоянного и переменного тока) используются элементы теории обобщенной электрической машины [2]. Без ее использования практически невозможно построить модель электродвигателей переменного тока.
Известно [2], что любая многофазная электрическая машина с nфазной обмоткой статора и mфазной обмоткой ротора при условии равенства полных сопротивлений фаз статора (ротора) для изучения динамических процессов может быть представлена эквивалентной двухфазной машиной.
Понятие обобщенной электрической машины
Обобщенная машина является упрощенной моделью реальной машины. Ее отличительными признаками являются:
Сосредоточенные в пазах проводники стоком заменены синусоидальными токовыми слоями, эквивалентными по магнитодинамической силе (МДС) первым гармоникам МДС соответствующих реальных обмоток.
Не учитывается неравномерность воздушного зазора, обусловленная пазами.
Наличие явнополюсной структуры на статоре (роторе) учитывается введением первой гармоники переменной составляющей зазора.
Магнитная цепь имеет очень высокую магнитную проницаемость и не насыщается, то есть считается, что энергия магнитного поля сосредоточена в воздушном зазоре. Влияние явнополюсности учитывается введением переменной радиальной магнитной проницаемости [2]
— соответственно электрической и геометрический угол поворота ротора относительно статора; 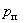
Полные сопротивления фаз статора и ротора равны.
Математическое описание процессов электромеханического преобразования энергии в обобщенной машине
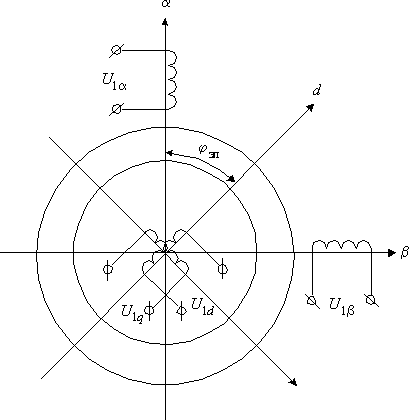
Обобщенная электрическая машина может быть представлена схемой приведенной на рис. 2.2. Две обмотки статора размещены в ортогональной системе координат 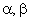
Рис. 2.2. Схема обобщенной машины
Для координат и параметров обобщенной машины будем использовать следующую систему индексов. Индексами 1 и 2 будем обозначать координаты и параметры, относящиеся соответственно к статору и ротору; индексы 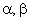
Динамика обобщенной электрической машины описывается четырьмя уравнениями электрического равновесия в цепях ее обмоток и уравнением электромеханического преобразования энергии. Уравнения электрического равновесия, выраженные через потокосцепления, и записанные относительно реальных напряжений и токов статора и ротора
где 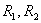
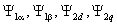
Уравнения (2.2) однотипны и их можно записать в компактной обобщающей форме:
где индекс i принимает значения 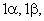
Потокосцепления обмоток в общем виде определяются результирующим действием токов всех обмоток машины:
Здесь для собственных и взаимных индуктивностей обмоток принято одинаковое обозначение с подстрочным индексом, первая часть которого i=

Однотипность записи уравнений (2.4) позволяет в дальнейшем прибегнуть к удобной обобщенной форме записи этой системы
При работе машины взаимное положение обмоток статора и ротора изменяется, поэтому собственные и взаимные индуктивности обмоток в общем случае являются функцией угла поворота ротора
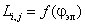
Для симметричной неянополюсной машины собственные индуктивности статора и ротора не зависят от положения ротора
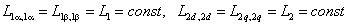
а взаимные индуктивности между обмотками статора или ротора равны нулю
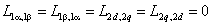
так как магнитные оси этих обмоток сдвинуты в пространстве на угол
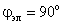
Взаимные индуктивности обмоток статора и ротора проходят полный цикл изменений при повороте ротора на угол
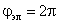
поэтому можно записать
С учетом выражения (2.5) уравнения электрического равновесия можно представить в обобщенной форме записи
где 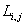
В результате взаимодействия токов, протекающих по обмоткам обобщенной машины, на ее роторе создается электромагнитный момент М, который может быть определен с помощью известных соотношений [2]:
С помощью выражения (2.5) электромагнитный момент может быть выражен через токи обмоток:
Уравнения электрического равновесия (2.7) в сочетании с уравнением электромагнитного момента (2.8) представляют собой математическое описание динамического процесса преобразования энергии, которое в дальнейшем будет конкретизировано для наиболее используемых разновидностей электродвигателей. В обобщенной форме это описание принимает следующий вид:
Уравнение электромагнитного момента можно упростить, подставив в (2.9) выражения для собственных и взаимных индуктивностей обмоток (2.6):
В электрическом двигателе осуществляется связь механического движения привода и приводимого им в движение механизма с электрическими процессами в системе автоматического управления и наоборот. Эта связь объединяет механическую и электрическую части в единую электромеханическую систему.
Так как 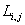
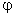
— угловая скорость вала двигателя.
Первый член каждого уравнения (2.12) представляет собой падение напряжения на активном сопротивлении цепи данной обмотки, второй результирующую ЭДС самоиндукции и взаимной индукции 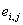
Следовательно, математическое описание процессов преобразования энергии в обобщенной электрической машине в общем виде имеет следующий вид:
Контрольные вопросы к лекции No 2.
Назовите основное условие возможности представления многофазной электрической машины с nфазной обмоткой статора и mфазной обмоткой ротора эквивалентной двухфазной машиной.
С какой скорость вращаются обмотки статора обобщенной электрической машины?
С какой скорость вращаются обмотки ротора обобщенной электрической машины?
Значения каких индуктивностей обмоток статора и ротора от угла поворота ротора 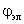
Поясните физический смысл полученных уравнений электрического равновесия напряжений в обмотках обобщенной электрической машины:
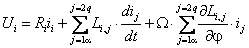
Полные сопротивления фаз статора и ротора должны быть соответственно равны.
Обмотки статора обобщенной электрической машины неподвижны в пространстве.
Обмотки ротора обобщенной электрической машины неподвижны относительно ротора и вращаются в пространстве со скоростью ротора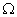
Взаимные индуктивности 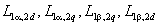
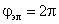
Первый член каждого уравнения представляет собой падение напряжения на активном сопротивлении цепи данной обмотки, второй результирующую ЭДС самоиндукции и взаимной индукции 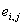
Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Лекция №4. Математическое описание процессов преобразования энергии
Цель лекции:
—ознакомить студентов ссистемой уравнений, описывающих процессы электромеханического преобразования энергии, дифференциальными уравнениями, описывающих переходные и установившиеся процессы в обобщенной машине, моделью обобщенного электромеханического преобразователя.
Содержание лекции:
— система уравнений, описывающих процессы электромеханического преобразования энергии;
— дифференциальные уравнения, описывающие переходные и установившиеся процессы в обобщенной машине;
— модель обобщенного электромеханического преобразователя.
Математическая модель электрической машины — это система уравнений, описывающих процессы электромеханического преобразования энергии с допущениями, обеспечивающими необходимую точность решения для рассматриваемой задачи. Математические модели электрических машин широко используются для исследования электромеханических систем благодаря применению аналоговых и цифровых вычислительных машин. В настоящее время созданы модели, позволяющие исследовать практически любые задачи, встречающиеся в электромашиностроении .
Несмотря на бесконечное конструктивное разнообразие индуктивных электрических машин все электрические машины с круговым полем в воздушном зазоре можно свести к обобщенной электрической машине. Обобщенная электрическая машина — это идеализированная двухполюсная машина с двумя парами обмоток на статоре и роторе. В ней энергия магнитного поля сосредоточена в воздушном зазоре и поле синусоидальное. В воздушном зазоре обобщенной машины вращающееся магнитное поле может создаваться обмотками статора и ротора. Напряжения статора или ротора создают сдвинутые во времени токи, а за счет пространственного сдвига обмоток в зазоре создается вращающееся поле.
Машины постоянного тока получаются из модели обобщенной электрической машины, если обмотки ротора или статора питать через преобразователь частоты.
В машинах постоянного тока преобразователем частоты является механический преобразователь частоты — коллектор. Постоянный ток преобразуется в многофазный переменный ток, который создает вращающееся поле, неподвижное относительно обмотки возбуждения, расположенной на статоре.
Как в машинах переменного, так и в машинах постоянного тока много фазная симметричная обмотка приводится к двухфазной, которая и рассматривается в обобщенной электрической машине. Процессы преобразования энергии в многополюсных машинах приводятся к процессам в двухполюсной машине.
Уравнения обобщенной электрической машины были предложены Г. Кроном в 30-х годах, и в последние десятилетия теория обобщенной машины получила дальнейшее развитие в работах советских и зарубежных ученых.
Рисунок 4.1 — Модель двухфазной машины в непреобразованной системе координат
Дифференциальные уравнения, описывающие переходные и установившиеся процессы в обобщенной машине в естественных или фазовых непреобразованных координатах (см. рисунок 4.1), имеют вид
ua s =ia s ra s +dψa s /dt;
В (4.1) потокосцепления обмоток
В (4.1) и (4.2) ua s , ub s , ua r , ub r — напряжения на обмотках статора и ротора ; ia s , ib s , i r , ib r — токи в обмотках статора и ротора; ra s , rb s , r r , rb r — активные сопротивления обмоток статора и ротора; La s , Lb s , L r , Lb r — индуктивности обмоток статора и ротора; М — взаимная индуктивность между обмотками статора и ротора; Ө — угол между осями обмоток статора и ротора.
Если подставить (4.2) в (4.1), получатся громоздкие уравнения с периодическими коэффициентами. Для упрощения уравнений электромеханического преобразования энергии рассматривается псевдонеподвижная машина, в которой в обмотки ротора вводится ЭДС вращения. При этом в неподвижной и вращающейся машинах токи, активная и реактивные мощности остаются неизменными.
В неподвижной системе координат α, δ уравнения обобщенной машины, выраженные через потокосцепления, выглядят следующим образом:
uα s = iα s rα s + 
uβ s = iβ s rβ s + 
uα s = iα s rα s + 
uβ s = iβ s rβ s + 
Подставляя в (4.4) значения потокосцеплений
получаем выраженные через токи уравнения напряжений для машины, которые удобно записывать в матричной форме:
| uα s |   0 0 0 0 | iα s | ||
| uα r uβ r | = |   Lβ r ωr Mωr — Mωr -Lα r ωr Lβ r ωr Mωr — Mωr -Lα r ωr   | X | iα r iβ r |
| uβ s | 0 0   | iβ s |
В (4.1)-(4.5) uα s , uβ s , uα r , uβ r , iα s , iβ s , iα r , iβ r , — соответственно напряжения и токи в обмотках статора и ротора по осям α и β; rα s , rβ s , rα r , rβ r , — активные сопротивления обмоток статора и ротора; М — взаимная индуктивность; Lα s , Lβ s , Lα r , Lβ r , — полные индуктивности обмоток статора и ротора по осям α и β ; ωr — угловая скорость ротора.
Индуктивности обмоток определяются по известным соотношениям
где lα s , lβ s , lα r , lβ r — индуктивности рассеяния обмоток статора и ротора по осям α и β.
Активные сопротивления и индуктивности в (4.4) относятся к фазе машины и определяются расчетным и опытным путем.
Применяя преобразования координат при инвариантной мощности, получают уравнения в других координатах.
Процессы преобразования энергии в переходных процессах описываются уравнениями напряжений (4.1) или (4.2) и уравнением движения
Mэ = 
где Мэ — электромагнитный вращающий момент — момент, создаваемый машиной; Мс — момент сопротивления с учетом момента трения; р — число пар полюсов; J — момент инерции.
Мэ 
где m — число фаз.
Вращающий момент может быть выражен:
через потокосцепления (4.5)
Мэ = 
через потокосцепления и токи статора:
Мэ = 
через потокосцепления и токи ротора:
Мэ = 
Справедливость (4.8) — (4.10) подтверждается, если в (4.9) подставить значения потокосцеплений и токов из (4.2). Вращающий момент после преобразований (4.9) — (4.10) может иметь и другой вид. Вращающий момент можно определить также через намагничивающие токи и через изменение энергии магнитного поля или из выражения вектора Пойнтинга.
При круговом поле в воздушном зазоре наращивание сложности уравнений происходит при учете нелинейностей параметров и учете нескольких контуров на статоре и роторе.
Уравнения электромеханического преобразования энергии усложняются при наличии двух полей в воздушном зазоре машины. При эллиптическом поле система уравнений электромеханического преобразования энергии состоит из восьми уравнений напряжения и уравнения электромагнитного момента с четырьмя парами произведений токов в обмотках статора и ротора. Число уравнений увеличивается при учете контуров с токами на статоре и роторе. Учет нескольких полей и контуров на статоре и роторе приводит к системе с несколькими десятками уравнений. Наиболее простая система уравнений — система уравнений третьего порядка — получается, если использовать описание процессов преобразования энергии через обобщенные векторы
U= 



Система уравнений (4.11) и уравнение движения (4.6) описывают динамические и статические характеристики электрической машины.
Уравнения установившегося режима получаются из дифференциальных уравнений путем замены в уравнениях электромеханического преобразования энергии оператора дифференцирования
d/dt 
В установившемся режиме уравнения напряжений и уравнение движения могут рассматриваться независимо друг от друга. Простейшие уравнения в установившемся режиме получаются из схем замещения электрических машин и упрощенных уравнений, на базе которых строятся векторные диаграммы. Круговое поле в воздушном зазоре может быть только в идеализированной машине. В воздушном зазоре реальной электрической машины имеется бесконечный произвольный спектр гармоник поля, состоящий из временных и пространственных гармоник. Высшие гармоники в воздушном зазоре машины появляются за счет несинусоидальности напряжений, несинусоидального распределения МДС, неравномерности зазора, насыщения и других причин.
Видео:Что такое РЕЗОНАНС НАПРЯЖЕНИЙ | САМОЕ ПОНЯТНОЕ объяснениеСкачать

Векторное управление асинхронными двигателями (стр. 2 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 |
Переход к неподвижной системе координат в уравнении ротора привел к разложению слагаемого, соответствующего ЭДС индукции, на две составляющие: первая составляющая d y 2 /dt связана с изменением потокосцепления во времени вследствие измерения во времени токов и называется ЭДС трансформации, по аналогии с процессами ее возбуждения в соответствующей электрической машине; вторая – w y 2 связана с изменением потокосцепления вследствие вращения ротора и называется ЭДС вращения. Разложение ЭДС индукции на составляющие является математической операцией, связанной с преобразованием системы координат при условии инвариантности мощности и в некоторых случаях это разложение можно истолковать, исходя из физических процессов в машине.
Уравнения (1.4.2) и (1.4.4) записаны для неподвижной системы координат и их можно объединить в общую систему для решения. Кроме того, оба этих уравнения можно представить в некоторой произвольной системе координат m-n, вращающейся с произвольной угловой частотой w (mn). Для этого с ними нужно проделать преобразования аналогичные выражениям (1.4.4) , в результате которых мы получим уравнения:

из которых уравнения для любых других систем координат получаются подстановкой в (1.4.5) соответствующей частоты вращения w (mn).
Выражения (1.4.5) показывают, что выбором системы координат можно упростить задачу, исключив ЭДС вращения, но только в одном из уравнений.
В дальнейшем мы будем использовать следующие индексы систем координат:
неподвижная система координат (
система координат, вращающаяся синхронно с ротором (
система координат, вращающаяся синхронно с потокосцеплением ротора (
произвольно ориентированная система координат, вращающаяся с произвольной скоростью 
В любой электрической машине угловая частота вращения магнитного поля статора W 1 связана с угловой частотой вращения магнитного поля ротора W 2 и угловой частотой вращения ротора W следующим соотношением – 


где 
1.5. Обобщенная электрическая машина.
Уравнения (1.4.3) и (1.4.4) , записанные в неподвижной системе координат a — b , можно разложить на составляющие, представив векторные величины в виде комплексных чисел
Уравнениям (1.5.1) соответствует электрическая машина с одной парой полюсов и двумя обмотками на статоре и роторе, расположенными на взаимно-перпендикулярных осях и неподвижными друг относительно друга (рис. 1.4). Такая электрическая машина называется обобщенной (ОЭМ).
При выводе уравнений (1.5.1) использовался ряд допущений, поэтому все они должны быть распространены и на модель обобщенной машины, т. е.:
1. машина симметрична и имеет равномерный воздушный зазор;
2. магнитопровод машины ненасыщен;
3. МДС обмоток имеет синусоидальное распределение по рабочему зазору.
Модель обобщенной электрической машины универсальна и при принятии определенных условий, из нее можно получить все типы электрических машин как частные случаи. Например, при питании обмоток статора от двух источников переменного синусоидального тока, смещенных по фазе на 90 ° , в рабочем зазоре создается круговое вращающееся магнитное поле. Если одну из обмоток ротора подключить к источнику постоянного тока, то мы получим модель синхронной машины. Если обе обмотки ротора замкнуть накоротко, то образуется модель асинхронной короткозамкнутой машины. Наконец, если одну из обмоток статора подключить к источнику постоянного тока, а обмотки ротора подключить к двум источникам переменного синусоидального тока с частотой, равной частоте вращения ротора, и фазовым смещением в 90 ° , таким образом, чтобы поле ротора вращалось в направлении противоположном направлению вращения его вала, то мы получим модель машины постоянного тока. В этой модели поле ротора формируется источниками питания переменного тока с управляемой частотой, роль которых в реальной машине играет источник постоянного тока и коллектор.
Уравнения (1.4.5) соответствуют модели обобщенной электрической машины в системе координат, вращающейся с произвольной угловой частой w (mn). Их также можно разложить на составляющие в виде

Уравнения (1.5.2) можно представить электрической схемой замещения рис. 1.5.
В короткозамкнутом АД 


При этом отсутствие внешнего источника электрической энергии, питающего ротор короткозамкнутого АД, определяет следующее соотношение частот статора и ротора в уравнениях (1.5.3) –

1.5.1. Электромагнитный момент АД.
Основной конечной величиной характеризующей электромеханическое преобразование является электромагнитный момент на валу. Он образуется в результате взаимодействия магнитного поля и тока, протекающего в обмотках статора или ротора, и может быть представлен как векторное произведение

где – zp число пар полюсов машины. Можно также, воспользовавшись выражениями (1.2.8) , представить его в виде –

В выражениях (1.5.5) и (1.5.6) физический смысл имеет только модуль вектора электромагнитного момента и его можно определить через проекции векторов сомножителей. Для произвольных векторов a и b модуль векторного произведения равен разности скалярных произведений проекций векторов на ортогональные оси координат, т. е. –
Поэтому любое из выражений (1.5.5) и (1.5.6) позволяет найти модуль электромагнитного момента |m|=m, выразив входящие в него векторы через их проекции на координатные оси m-n. Например, электромагнитный момент определяется через произведение потокосцепления ротора на ток ротора в виде

1.6. Модель короткозамкнутого АД при частотном управлении.
Асинхронный привод с частотным управлением является в настоящее время наиболее распространенным. Однако его динамика чаще всего исследуется с помощью упрощенных моделей с отклонениями в малом. Векторная модель АД позволяет получить точную структурную схему, которую затем можно исследовать современными средствами компьютерного моделирования. Рассмотрим на этом примере методику получения передаточных функций сложных объектов с помощью векторных уравнений ОЭМ.
Пусть система координат модели АД ориентирована по вектору напряжения статора. Тогда ее угловая частота вращения будет определяться частотой сети 



Для вычисления модуля электромагнитного момента АД m используем векторы потокосцепления статора 



где 
При указанном выборе векторов, определяющих электромагнитный момент, нужно с помощью выражений (1.2.8) исключить в уравнениях (1.6.2) и (1.6.3) векторы 


где: 


Вычитая из уравнения (1.6.4) уравнение (1.6.5), можно понизить порядок уравнения –
где: 

Разделим векторы в выражении (1.6.6) на вещественные и мнимые составляющие и выразим проекции тока ротора
Выражения (1.6.7) позволяют построить структурную схему преобразования напряжения 







Разделяя вещественную и мнимую составляющие, получим


Как следует из рисунка, структура АД нелинейна и имеет четыре перекрестных связи. Упростить ее для получения передаточных функций по каналам управления напряжением и частотой крайне затруднительно, но не представляет большого труда построить эту модель в системе MatLab/Simulink и получить требуемые характеристики привода при различных законах управления, связывающих какой-либо функцией U=F( w 1 ) входы управления частотой и напряжением статора.
2. ВЕКТОРНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМ ДВИГАТЕЛЕМ
2.1 Общий принцип векторного управления АД.
Как известно, полная управляемость электропривода обеспечивается, если обеспечивается управление электромагнитным моментом двигателя. В случае АД для построения системы управления можно использовать выражения (1.5.5) – (1.5.6) и другие производные от этих выражений. Для этого требуется независимо управлять координатами векторов, входящих в выбранное уравнение электромагнитного момента. Выбор уравнения для построения системы управления играет большую роль, т. к. многие величины, в особенности у короткозамкнутых АД, не могут быть измерены. Кроме того, этот выбор существенно влияет на сложность передаточных функций системы, иногда в несколько раз увеличивая порядок уравнений. Однако при любом выборе структура выражения электромагнитного момента будет аналогичной (1.5.7) и общий принцип моделирования и построения системы управления АД заключается в том, что для этого используется система координат, постоянно ориентированная по направлению какого-либо вектора, определяющего электромагнитный момент. Тогда проекция этого вектора на другую ось координат и соответствующее ей слагаемое в выражении для электромагнитного момента будут равны нулю, и формально оно принимает вид, идентичный выражению для электромагнитного момента двигателя постоянного тока, который пропорционален по величине току якоря и основному магнитному потоку.
Выбор вектора, по направлению которого ориентируется координатная система, произволен и определяется только простотой и возможностью реализации модели АД. Например, в случае ориентации по потокосцеплению ротора (


Очевидно, что первое выражение для управления короткозамкнутым АД не представляет интереса, т. к. включает практически неподдающийся измерению и управлению ток ротора, в то время как второе, позволяет при условии постоянства потокосцепления ротора управлять электромагнитным моментом изменением проекции тока статора на поперечную ось i1q.
Таким образом, для построения системы векторного управления АД нужно выбрать вектор, относительно которого будет ориентирована система координат, и соответствующее выражение для электромагнитного момента, а затем определить, входящие в него величины из уравнений (1.5.3) для цепи статора и/или ротора.
2.2. Модель АД, управляемого током статора, в системе координат, ориентированной по потокосцеплению ротора.
Если в качестве опорного вектора выбрать потокосцепление ротора и ориентировать по нему координатную систему так, чтобы ее вещественная ось совпадала с направлением y 2,то угловая частота вращения системы координат w (mn)= w (dq) будет равна угловой частоте питания статора w 1, т. к. векторы потокосцеплений статора и ротора вращаются с одинаковой частотой. Тогда из уравнения (1.5.3) для цепи ротора и с учетом того, что w 1 — w = w 2, уравнение ротора имеет вид

В это уравнение в качестве переменной входит неконтролируемый ток ротора. Поэтому из выражения (1.2.8 б) для потокосцепления y 2 найдем 

Преобразуем уравнение (2.2.2) по Лапласу и введем в него электромагнитную постоянную времени ротора 

Отсюда найдем проекции вектора тока статора с учетом того, что y 2q=0
а также потокосцепление и угловую частоту ротора
Таким образом, с помощью проекции тока статора i1d можно управлять потокосцеплением ротора и передаточная функция этого канала соответствует апериодическому звену с постоянной времени равной постоянной времени ротора; а с помощью проекции i1q можно независимо и безинерционно управлять частотой ротора w 2.
Подставляя i1q в выражение (2.1.1) , получим

т. е. частота токов ротора при заданном потокосцеплении определяет электромагнитный момент АД.

🎥 Видео
Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Электромагнитная индукция│ПРОСТЫМИ СЛОВАМИ в теории и на опытахСкачать

Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

Решение биквадратных уравнений. 8 класс.Скачать

Основное уравнение динамики вращательного движения. 10 класс.Скачать

Лабораторная работа №5 по физике для 8 класса "Измерение напряжения на различных участках цепи"Скачать

РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Резонанс напряжений в электрической цепи. 11 класс.Скачать

Активное и реактивное сопротивление в цепи переменного тока. 11 класс.Скачать

Физика. 11 класс. Резонанс напряжений в электрической цепи /15.10.2020/Скачать

Последовательное и Параллельное Соединение Проводников // Физика 8 классСкачать

Яковкина Т.Н. Проблема наведенных напряжений в электросетяхСкачать

Связь между напряженностью электростатического поля и напряжением | Физика 10 класс #51 | ИнфоурокСкачать

Урок 218. Напряженность электрического поляСкачать

2020 г. Дифференциальные уравнения для электрических цепей. Лекция и практикаСкачать

Резонанс напряжений в электрической цепиСкачать