Уравнения на возрастание и убывание функции

Видео:Свойства функции. Промежутки возрастания и убывания функции. 10 класс.Скачать

Интервалы возрастания и убывания функции

Видео:Возрастание функции | убывание функции | 9 класс МакарычевСкачать

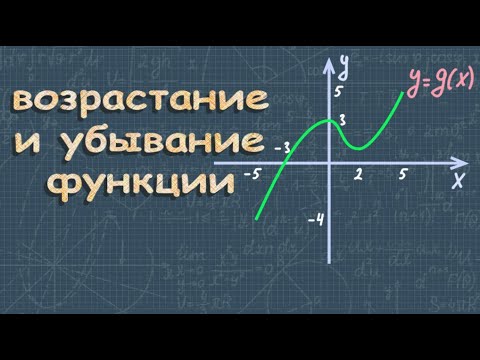
Исследование функции с помощью производной

Определение : Точка х₀ называется точкой локального минимума, если для любого х из окрестности точки х₀ выполняется неравенство: f(x₀) .
Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.
Точками экстремума могут служить только критические точки I рода, т.е. точки, принадлежащие области определения функции, в которых производная f′(x) обращается в нуль или терпит разрыв.

Правило нахождения экстремумов функции y=f(x) с помощью первой производной

1. Найти производную функции f′(x) .
2. Найти критические точки по первой производной, т.е. точки, в которых производная обращается в нуль или терпит разрыв.
3. Исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции f(x) . Если на промежутке f′(x) , то на этом промежутке функция убывает; если на промежутке f′(x)>0 , то на этом промежутке функция возрастает.
4. Если в окрестности критической точки f′(x) меняет знак с «+» на «-», то эта точка является точкой максимума, если с «-» на «+», то точкой минимума.
5. Вычислить значения функции в точках минимума и максимума.

С помощью приведенного алгоритма можно найти не только экстремумы функции, но и промежутки возрастания и убывания функции.

Пример №1 : Найти промежутки монотонности и экстремумы функции: f(x)=x 3 –3x 2 .
Решение: Найдем первую производную функции f′(x)=3x 2 –6x.
Найдем критические точки по первой производной, решив уравнение 3x 2 –6x=0; 3x(x-2)=0 ;x = 0, x = 2

Исследуем поведение первой производной в критических точках и на промежутках между ними.

f(0) = 0 3 – 3*0 2 = 0
f(2) = 2 3 – 3*2 2 = -4
Ответ: Функция возрастает при x∈(-∞ ; 0)∪(2; +∞); функция убывает при x∈(0;2);
точка минимума функции (2;-4); точка максимума функции (0;0).

Правило нахождения экстремумов функции y=f(x) с помощью второй производной

1. Найти производную f′(x) .
2. Найти стационарные точки данной функции, т.е. точки, в которых f′(x)=0 .
3. Найти вторую производную f″(x) .
4. Исследовать знак второй производной в каждой из стационарных точек. Если при этом вторая производная окажется отрицательной, то функция в такой точке имеет максимум, а если положительной, то – минимум. Если же вторая производная равна нулю, то экстремум функции надо искать с помощью первой производной.
5. Вычислить значения функции в точках экстремума.

Отсюда следует, что дважды дифференцируемая функция f(x) выпукла на отрезке [a, b], если вторая производная f»(x) ≥ 0 при всех х [a, b].

Все вычисления можно проделать в онлайн режиме.

Пример №2 . Исследовать на экстремум с помощью второй производной функцию: f(x) = x 2 – 2x — 3.
Решение: Находим производную: f′(x) = 2x — 2.
Решая уравнение f′(x) = 0, получим стационарную точку х =1. Найдем теперь вторую производную: f″(x) = 2.
Так как вторая производная в стационарной точке положительна, f″(1) = 2 > 0, то при x = 1 функция имеет минимум: f_min = f(1) = -4.
Ответ: Точка минимума имеет координаты (1; -4).

Видео:Промежутки возрастания и убывания функции. 10 класс.Скачать

Использование возрастания и убывания при решении уравнений

Одно из направлений функционально-графического метода решения уравнений связано с использованием возрастания и убывания функций, отвечающих частям уравнения. В этой статье мы подробно разберем соответствующий метод решения уравнений. Сначала скажем, для решения каких уравнений он предназначен, в чем он состоит, на чем базируется, и приведем его обоснование. Далее запишем алгоритм метода и дадим рекомендации к проведению его шагов. Наконец, рассмотрим решения характерных примеров.

Видео:Возрастание и убывание функций. Математика 9 класс.Скачать

Какие уравнения решаются через возрастание/убывание?

Для начала следует разобраться, какие уравнения могут быть решены посредством использования возрастания/убывания функций, отвечающих частям уравнения.

Во-первых, это уравнения f(x)=C , где f(x) – некоторое выражение с переменной x , а C – некоторое число, причем эти уравнения должны удовлетворять следующим критериям:

• Не видно альтернативных более простых методов решения уравнения.
• ОДЗ для уравнения есть некоторый числовой промежуток (позже в этом пункте мы скажем и про уравнения, ОДЗ для которых есть не отдельный числовой промежуток, а объединение нескольких промежутков).
• Есть возможность определить корень уравнения каким-либо способом, часто путем подбора.
• Есть возможность доказать возрастание или убывание функции f .

В качестве примера приведем уравнение . Это уравнение вида f(x)=C , где , C=4 . Сразу видно, что для решения этого уравнения может подойти разве что функционально-графический метод, так как переменная находится под знаками «разнородных» функций: функции извлечения корня и функции арктангенс. Причем строить график функции, отвечающей левой части уравнения, довольно сложно. Более простых привычных способов решения не видно. ОДЗ для этого уравнения определяется условием , откуда находим, что ОДЗ есть числовой промежуток . Учитывая рекомендации по определению корней уравнения, которые мы дадим в одном из следующих пунктов текущей статьи, несложно подобрать корень уравнения, им является число 1 . Рекомендации по обоснованию возрастания/убывания, которые мы также дадим чуть позже, позволяют показать возрастание функции, отвечающей левой части уравнения. То есть, выполняются все критерии, которым должно удовлетворять уравнение для его решения посредством использования возрастания/убывания.

Во-вторых, через возрастание/убывание решаются уравнения f(x)=g(x) , где f(x) и g(x) – это некоторые выражения с переменной x , удовлетворяющие следующим критериям:

• Не видно других более простых методов решения.
• ОДЗ для уравнения есть отдельный числовой промежуток (про уравнения, ОДЗ для которых есть объединение нескольких числовых промежутков, скажем чуть позже).
• Есть возможность определить корень уравнения.
• Есть возможность доказать возрастание одной из функций f или g и убывание другой.

Поясним на примере. Для этого подойдет уравнение . Это уравнение вида f(x)=g(x) , где и . Здесь переменная есть в показателе степени и под знаком натурального логарифма. Это сразу существенно ограничивает набор методов, подходящих для его решения, оставляя только функционально-графический или какие-либо специфические методы. Графики здесь мало что дают в плане нахождения корней. Остается опираться лишь на свойства функций. При этом легко определить область допустимых значений переменной x для уравнения, она представляет собой числовой промежуток . Также легко подбирается корень уравнения, им является число 3 , и легко обосновывается убывание функции, отвечающей левой части уравнения, и возрастание функции, отвечающей правой части уравнения. Значит, это уравнение может быть решено посредством использования возрастания/убывания.

Теперь про уравнения f(x)=C и f(x)=g(x) , ОДЗ для которых есть объединение нескольких числовых промежутков. Если они на отдельно взятом промежутке области допустимых значений удовлетворяют записанным выше критериям, то на этом промежутке можно получить их решение посредством использования возрастания/убывания. Если это сделать на каждом промежутке области допустимых значений, то будет получено решение уравнения в целом.

И вновь обратимся к конкретному примеру. Рассмотрим уравнение . Для него не просматривается простое решения привычными методами, отличными от направления функционально-графического метода, подразумевающего использование возрастания/убывания. ОДЗ для этого уравнения представляет собой не отдельно взятый числовой промежуток, а объединение двух числовых промежутков (−∞, 0) и (0, +∞) . На каждом из этих промежутков несложно подобрать корни уравнения. Корнем на первом промежутке является число −8 , а на втором – число 27 . Также на каждом промежутке легко обосновать убывание функции, отвечающей левой части уравнения, и возрастание функции, отвечающей правой части уравнения. Значит, это уравнение может быть решено через возрастание/убывание.

То есть, решение уравнений f(x)=C и f(x)=g(x) , ОДЗ для которых есть объединение нескольких числовых промежутков, сводится к решению этих уравнений на отдельно взятых промежутках. По этой причине метод решения можно постигать на уравнениях f(x)=C и f(x)=g(x) , ОДЗ для которых представляет отдельный числовой промежуток.

Видео:Возрастание и убывание функции от bezbotvyСкачать

В чем состоит метод и на чем он базируется

Метод состоит в нахождении корней решаемого уравнения любым доступным способом, часто подбором, и использовании возрастания/убывания для доказательства того, что других корней нет.

В основе метода лежат два следующих утверждения:

Если функция y=f(x) определена и возрастает или убывает на некотором промежутке X , и уравнение f(x)=C , где C – некоторое число, имеет корень на X , то этот корень единственный на X .

Если функции y=f(x) и y=g(x) определены на некотором промежутке X , причем одна из них убывает на этом промежутке, а другая – возрастает, и если уравнение f(x)=g(x) имеет на X корень, то этот корень единственный на X .

Видео:АЛГЕБРА 9 класс. Возрастающая и убывающая функцииСкачать

Обоснование метода

Начнем с доказательства первого утверждения.

Пусть функция y=f(x) определена и возрастает или убывает на промежутке X , и пусть x₀ – корень уравнения f(x)=C , где C – некоторое число, причем x₀∈X . Докажем, что x₀ – единственный корень уравнения f(x)=C на промежутке X .

Предположим, что уравнение имеет еще один корень на X , отличный от x₀ , обозначим его x₁ . Так как x₀ и x₁ — корни уравнения f(x)=C , то числовые равенства f(x₀)=C и f(x₁)=C – верные. Осуществив почленное вычитание этих числовых равенств, получим верное числовое равенство f(x₀)−f(x₁)=0 (см. свойства числовых равенств), откуда f(x₀)=f(x₁) . Но последнее равенство невозможно, так как функция f возрастающая или убывающая на X . Так методом от противного доказано, что x₀ – единственный корень.

Теперь докажем второе утверждение.

Пусть функции y=f(x) и y=g(x) определены на промежутке X , одна из них возрастает, пусть это будет функция f , а другая функция g – убывает, и пусть уравнение f(x)=g(x) имеет на X корень x₀ . Докажем, что x₀ – единственный корень указанного уравнения на X . (Можно считать, что f – убывающая функция, а g – возрастающая, доказательство при этом аналогично).

Предположим, что уравнение f(x)=g(x) имеет еще один корень на X , отличный от x₀ , обозначим его x₁ . Так как корни x₀ и x₁ – корни уравнения f(x)=g(x) , то f(x₀)=g(x₀) и f(x₁)=g(x₁) — верные числовые равенства. Так как корни x₀ и x₁ различные, то либо x₀ , либо x₀>x₁ . Разберем эти случаи по очереди.

Пусть x₀ . При этом, так как функция f — возрастающая, то f(x₀) , откуда f(x₁)>f(x₀) , а так как функция g – убывающая, то g(x₀)>g(x₁) . Из неравенства f(x₁)>f(x₀) и равенства f(x₀)=g(x₀) следует, что f(x₁)>g(x₀) , а из этого неравенства и неравенства g(x₀)>g(x₁) в силу свойства транзитивности (см. свойства числовых неравенств) следует, что f(x₁)>g(x₁) . Полученное неравенство означает, что x₁ не является корнем уравнения f(x)=g(x) , что противоречит нашему предположению.

Пусть x₀>x₁ . При этом, так как функция f — возрастающая, то f(x₀)>f(x₁ ), откуда f(x₁) , а так как функция g – убывающая, то g(x₀) . Из неравенства f(x₁) и равенства f(x₀)=g(x₀) следует, что f(x₁) , а из этого неравенства и неравенства g(x₀) в силу свойства транзитивности следует, что f(x₁) . Полученное неравенство означает, что x₁ не является корнем уравнения f(x)=g(x) , опять получили противоречие нашему предположению.

Так методом от противного доказано второе утверждение из предыдущего пункта.

Видео:АЛГЕБРА С НУЛЯ — Точки Экстремума ФункцииСкачать

Алгоритмы метода

Сначала запишем алгоритмы решения уравнений f(x)=C и f(x)=g(x) , ОДЗ для которых есть числовой промежуток. После этого запишем алгоритм для случаев, когда ОДЗ представляет собой объединение нескольких числовых промежутков. Разъяснения к проведению шагов будут даны в следующих пунктах этой статьи.

Алгоритм решения уравнения f(x)=C , для которого ОДЗ есть числовой промежуток, посредством использования возрастания/убывания:

• Находим ОДЗ, убеждаемся, что она представляет собой некоторый числовой промежуток.
• Определяем корень уравнения любым доступным способом.
• Доказываем возрастание или убывание функции f . Это позволит утверждать, что найденный на предыдущем шаге корень является единственным корнем решаемого уравнения.

Алгоритм решения уравнения f(x)=g(x) , для которого ОДЗ есть числовой промежуток, через использование возрастания/убывания:

• Определяем ОДЗ, убеждаемся, что она представляет собой некоторый числовой промежуток.
• Определяем корень уравнения любым доступным способом.
• Доказываем возрастание одной из функций, отвечающих частям решаемого уравнения, и убывание другой. После этого можно делать вывод, что найденный на предыдущем шаге корень является единственным.

Для решения уравнений f(x)=C и f(x)=g(x) , ОДЗ для которых есть объединение нескольких числовых промежутков, посредством использования возрастания/убывания, надо проделать шаги, аналогичные шагам записанных алгоритмов, но на каждом отдельно взятом промежутке, составляющем ОДЗ, после чего взять объединение всех найденных корней.

То есть, для решения уравнения f(x)=C через возрастание/убывание, надо

• Определить ОДЗ.
• На каждом промежутке, составляющем ОДЗ, определить корень любым доступным способом.
• На каждом промежутке доказать убывание или возрастание функции f .
• Взять объединение корней, найденных на втором шаге. Это и есть искомое решение.

А для решения уравнения f(x)=g(x) через возрастание/убывание, надо

• Определить ОДЗ.
• На каждом промежутке, составляющем ОДЗ, определить корень любым доступным способом.
• На каждом промежутке доказать убывание одной из функций f или g , и возрастание другой функции.
• Взять объединение корней, найденных на втором шаге. Это и есть искомое решение.

Видео:10 класс, 44 урок, Применение производной для исследования функций на монотонность и экстремумыСкачать

Рекомендации к определению корня

Корень характерных уравнений, которые решаются посредством использования возрастания/убывания, либо очевиден, либо довольно легко находится подбором. Дадим рекомендации, которые обычно позволяют справиться с подбором корня.

Первая рекомендация касается случаев, когда ОДЗ для уравнения представляет собой числовой отрезок, числовой полуинтервал или числовой интервал, содержащий некоторое небольшое количество целых чисел. В этих случаях корнем уравнения часто бывает одно из целых чисел области допустимых значений или одна из границ ОДЗ. Приведем пример.

В качестве примера возьмем уравнение . Его ОДЗ есть числовой отрезок [−1/3, 1] . Подбор корня стоит начинать с границ ОДЗ и целых чисел, входящих в ОДЗ. В нашем случае это числа −1/3 , 0 и 1 . Осуществив проверку подстановкой, выясняем, что 1 – корень уравнения.

Переходим ко второй рекомендации по подбору корня. Корнем уравнения часто служит число, при котором находятся точные значения составляющих это уравнение выражений (корней, степеней, логарифмов, тригонометрических функций и т.д.). Примеры возьмем из первого пункта текущей статьи.

Взглянем на первое уравнение . Мы знаем точные значения арктангенса лишь семи чисел . А при каком значении переменной из этих семи мы можем извлечь корень ? Лишь при x=1 . Значит, число 1 – лучший кандидат в корни уравнения. Проверка показывает, что это число действительно является корнем уравнения.

Теперь взглянем на второе уравнение . Для каких значений переменной мы можем вычислить и значение степени , и значение логарифма ? Очевидно, для x=3 . Проверка подстановкой показывает, что это число есть корень уравнения.

Еще мы приводили в пример уравнение . Напомним, что ОДЗ для этого уравнения состоит из двух промежутков (−∞, 0) и (0, +∞) . Здесь приходится подбирать по корню в каждом промежутке. Подбор корней целесообразно начинать с перебора целых чисел, из которых извлекается кубический корень. Это кубы целых чисел, то есть, числа ±1, ±8, ±27, ±64, … Дальше можно пробовать дроби ±1/8, ±1/27, … В нашем случае до дробей дело не доходит, так как корнем первого промежутка оказывается −8 , а корнем второго промежутка оказывается число 27 .

Две приведенные рекомендации позволяют подобрать корень уравнения в подавляющем большинстве случаев, когда этого вообще возможно сделать без обладания сверхспособностями.

Видео:Промежутки возрастания и убыванияСкачать

Рекомендации к обоснованию возрастания/убывания функций

Одним из путей доказательства возрастания или убывания функции является обращение к производной (см. нахождение промежутков возрастания/убывания функции). Например, через производную можно доказать, что на ОДЗ для уравнения функция, отвечающая левой части уравнения, возрастает, а функция, отвечающая правой части, — убывает.

Однако иногда можно обойтись без обращения к производной. Разберемся когда.

В первую очередь, не обязательно обращаться к производной для доказательства возрастания/убывания, когда мы имеем дело с хорошо изученными функциями, в частности, основными элементарными. Например, нам совсем не обязательно доказывать возрастание функции y=x 7 на промежутке (−7, 1) через производную, мы и так прекрасно знаем, что эта степенная функция возрастает на всей области определения, значит, она возрастает и на указанном промежутке.

Также для обоснования возрастания/убывания удобно привлекать свойства возрастающих и убывающих функций. Перечислим основные свойства, имеющие непосредственное отношение к нашей теме:

• Если функция y=f(x) возрастает (убывает) на некотором числовом промежутке X , то функция y=f(x)+C , где C – некоторое число, тоже возрастает (убывает) на X . Приведем пример использования записанного свойства. Допустим, нас интересует, как ведет себя функция y=arccosx−4 на интервале (−0,5, 0,1) . Мы знаем, что функция y=arccosx убывает на всей области своего определения [−1, 1] , значит, она убывает и на интервале (−0,5, 0,1) . Тогда, оперевшись на записанное свойство, мы можем утверждать, что функция y=arccosx−4 тоже убывает на (−0,5, 0,1) .
• Если функция y=f(x) возрастает на числовом промежутке X , то функция y=k·f(x) при k>0 возрастает на X , а при k убывает на X . Если функция y=f(x) убывает на числовом промежутке X , то функция y=k·f(x) при k>0 убывает на X , а при k возрастает на X . Приведем пример. Допустим, столкнувшись с задачей решить некоторое уравнение, мы пришли к выводу, что оно может быть решено посредством использования возрастания/убывания. Нашли ОДЗ для этого уравнения, ею оказался промежуток [0, +∞) . Подобрали корень – число 9 . Доказали, что функция, отвечающая левой части уравнения возрастает на множестве [0, +∞) . И осталось доказать, что функция , отвечающая правой части уравнения, убывает на [0, +∞) . Как это сделать с использованием записанного свойства? Очень просто. Мы знаем, что функция — возрастает на [0, +∞) . Значит, в силу записанного свойства, функция убывает на [0, +∞) .
  • Следствие. Если функция y=f(x) возрастает (убывает) на X , то функция y=−f(x) убывает (возрастает) на X . Например, степенная функция убывает на промежутке (0, +∞) , значит, функция возрастает на этом промежутке (0, +∞) .
• Если функции y=f₁(x) и y=f₂(x) возрастающие (убывающие) на промежутке X , то функция y=f₁(x)+f₂(x) – возрастающая (убывающая) на X . Это свойство естественным образом распространяется на три и большее количество функций. Для удобства запоминания условно можно считать, что сумма возрастающих функций есть возрастающая функция, а сумма убывающих – убывающая функция. Например, функция y=x+x 3 +x 7 – возрастающая на множестве R , так как каждая из функций y=x , y=x 3 , y=x 7 возрастает на R . Другой пример: — убывающая на промежутке (0, +∞) как сумма убывающей показательной функции и убывающей логарифмической функции .
• Следующее свойство относится к сложным функциям. Приведем его условную формулировку, так как она хорошо запоминается из-за схожести с правилами умножения чисел с разными знаками. Возрастающая от возрастающей и убывающая от убывающей есть функция возрастающая, а возрастающая от убывающей и убывающая от возрастающей есть функция убывающая. Здесь придется привести несколько примеров. Для начала рассмотрим функцию и определим ее поведение на промежутке [3, 9] . Мы имеем дело со сложной функцией. Внутренняя функция – это логарифмическая функция , внешняя функция – это степенная функция . Так как основание логарифмической функции меньше единицы, то она убывает на всей своей области определения. Так как показатель степенной функции равен −1/2 , то функция убывает на своей области определения. Тогда функция возрастает на своей области определения как убывающая от убывающей. В частности, она возрастает на интересующем нас промежутке [3, 9] . Другой пример. Как ведет себя функция ? Убывает как возрастающая от возрастающей от убывающей.
  • Следствие. Если функция y=f(x) возрастает (убывает) на некотором числовом промежутке X и не обращается на нем в нуль, то функция y=1/f(x) убывает (возрастает) на X . Например, функция y=1/arcctgx – возрастает на всей области определения, так как функция y=arcctgx на своей области определения убывает и не обращается в нуль.

Умелое использование перечисленных свойств в соответствующих случаях дает возможность чуть ли не с одного взгляда на функцию определять ее возрастание или убывание.

Наконец, иногда для обоснования возрастания или убывания функции удобно использовать не производную, а определение возрастающей и убывающей функции в купе со свойствами верных числовых неравенств. Для примера обоснуем, что функция — возрастает на промежутке . Нам хорошо известно поведение функций и y=tgx , и мы можем сразу сказать, что на указанном промежутке они возрастают. Пусть x₁ и x₂ два числа из промежутка , причем x₁ . Тогда, в силу возрастания функций и y=tgx , верны числовые неравенства и tgx₁ . Также мы знаем, что функции и y=tgx на промежутке принимают только положительные значения, значит , tgx₁>0 , tgx₂>0 . Все это позволяет нам опереться на свойство умножения верных числовых неравенств одинакового смысла (см. свойства числовых неравенств), почленно перемножить неравенства и tgx₁ , что дает верное числовое неравенство . Из этого неравенства и определения возрастающей функции следует, что функция возрастает на промежутке .

Видео:Алгебра 11 класс (Урок№15 - Возрастание и убывание функции.)Скачать

Решение примеров

На страницах школьных учебников алгебры, начиная с 9 класса, встречается немало уравнений, решенных посредством обращения к возрастанию/убыванию соответствующих функций. В 9 классе изучаются степенные функции с натуральным показателем, после чего, естественно, показывается применение степенных функций и их свойств к решению уравнений. В этом свете в учебнике Мордковича представлено решение уравнения x 5 =3−2·x сначала графическим методом, затем – методом, предполагающим использование возрастания/убывания, причем сначала приведено утверждение, на котором базируется метод, с доказательством [1, с.120-121]. С решением этого уравнения все просто: легко подбирается корень x=1 , очевидно возрастание степенной функции y=x 5 и убывание линейной функции y=3−2·x , откуда следует, что найденный корень является единственным.

В учебнике для 10 классов в рамках разговора про обратные тригонометрические функции приводится решение уравнения [2, с. 163]. Там к возрастанию и убыванию обращаются для строгого обоснования единственности корня x=1 , который находится графически. Позже изучается производная и ее применение к исследованию функций на монотонность. Под эту тему приходится кстати уравнение 5·cosx+sin(4·x)−10·x=x 3 +5 [2, с. 354]. Оно решается посредством использования возрастания/убывания: корень x=1 легко подбирается, возрастание функции, отвечающей правой части уравнения, очевидно, а убывание функции, отвечающей левой части уравнения, доказывается через производную, так доказывается единственность найденного корня. Решение более сложного уравнения , в котором для доказательства убывания/возрастания привлекается производная, можете посмотреть здесь.

В 11 классе в арсенал учащихся добавляются степенные функции с дробным показателем и иррациональным показателем, показательные и логарифмические функции. Естественно, там же встречаются соответствующие уравнения, решение которых завязано на использовании свойств этих функций, например, , и lgx=11−x [3, с. 62, 93, 111]. Они являются типичными представителями уравнений, которые решаются через подбор корня и доказательство его единственности через обоснование возрастания одной из функций, отвечающих его частям, и убывание другой.

Давайте покажем полное решение одного из уравнений, которые мы приводили в пример в первом пункте этой статьи.

Решите уравнение

Видео:13A.1 Найдите промежутки возрастания и убывния функции f(x), заданной графикомСкачать

Возрастание и убывание функции на интервале, экстремумы

Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.

Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.

Видео:Промежутки возрастания и убывания функции. Практическая часть. 10 класс.Скачать

Возрастание и убывание функции на интервале

Функция y = f ( x ) будет возрастать на интервале x , когда при любых x 1 ∈ X и x 2 ∈ X , x 2 > x 1 неравенство f ( x 2 ) > f ( x 1 ) будет выполнимо. Иначе говоря, большему значению аргумента соответствует большее значение функции.

Функция y = f ( x ) считается убывающей на интервале x , когда при любых x 1 ∈ X , x 2 ∈ X , x 2 > x 1 равенство f ( x 2 ) > f ( x 1 ) считается выполнимым. Иначе говоря, большему значению функции соответствует меньшее значение аргумента. Рассмотрим рисунок, приведенный ниже.

Замечание: Когда функция определенная и непрерывная в концах интервала возрастания и убывания, то есть ( a ; b ) , где х = а , х = b , точки включены в промежуток возрастания и убывания. Определению это не противоречит, значит, имеет место быть на промежутке x .

Основные свойства элементарных функций типа y = sin x – определенность и непрерывность при действительных значениях аргументах. Отсюда получаем, что возрастание синуса происходит на интервале — π 2 ; π 2 , тогда возрастание на отрезке имеет вид — π 2 ; π 2 .

Видео:Математика без Ху!ни. Исследование функции, график. Первая, вторая производная, асимптоты.Скачать

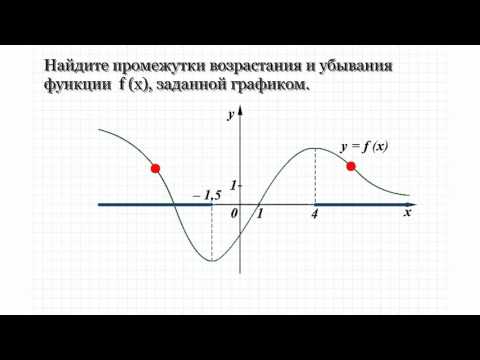
Точки экстремума, экстремумы функции

Точка х 0 называется точкой максимума для функции y = f ( x ) , когда для всех значений x неравенство f ( x 0 ) ≥ f ( x ) является справедливым. Максимум функции – это значение функции в точке, причем обозначается y m a x .

Точка х 0 называется точкой минимума для функции y = f ( x ) , когда для всех значений x неравенство f ( x 0 ) ≤ f ( x ) является справедливым. Минимум функции – это значение функции в точке, причем имеет обозначение вида y m i n .

Окрестностями точки х 0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.

Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.

Первый рисунок говорит о том, что необходимо найти наибольшее значение функции из отрезка [ a ; b ] . Оно находится при помощи точек максимума и равняется максимальному значению функции, а второй рисунок больше походит на поиск точки максимума при х = b .

Видео:Промежутки возрастания и убывания функции. Практическая часть. 10 класс.Скачать

Достаточные условия возрастания и убывания функции

Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.

Видео:§49 Возрастание и убывание функцииСкачать

Первое достаточное условие экстремума

Пусть задана функция y = f ( x ) , которая дифференцируема в ε окрестности точки x 0 , причем имеет непрерывность в заданной точке x 0 . Отсюда получаем, что

• когда f ‘ ( x ) > 0 с x ∈ ( x 0 — ε ; x 0 ) и f ‘ ( x ) 0 при x ∈ ( x 0 ; x 0 + ε ) , тогда x 0 является точкой максимума;
• когда f ‘ ( x ) 0 с x ∈ ( x 0 — ε ; x 0 ) и f ‘ ( x ) > 0 при x ∈ ( x 0 ; x 0 + ε ) , тогда x 0 является точкой минимума.

Иначе говоря, получим их условия постановки знака:

• когда функция непрерывна в точке x 0 , тогда имеет производную с меняющимся знаком, то есть с + на — , значит, точка называется максимумом;
• когда функция непрерывна в точке x 0 , тогда имеет производную с меняющимся знаком с — на + , значит, точка называется минимумом.

Видео:Возрастание. Убывание. Increasing and Decreasing FunctionsСкачать

Алгоритм для нахождения точек экстремума

Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:

• найти область определения;
• найти производную функции на этой области;
• определить нули и точки, где функция не существует;
• определение знака производной на интервалах;
• выбрать точки, где функция меняет знак.

Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.

Найти точки максимума и минимума заданной функции y = 2 ( x + 1 ) 2 x — 2 .

Область определения данной функции – это все действительные числа кроме х = 2 . Для начала найдем производную функции и получим:

y ‘ = 2 x + 1 2 x — 2 ‘ = 2 · x + 1 2 ‘ · ( x — 2 ) — ( x + 1 ) 2 · ( x — 2 ) ‘ ( x — 2 ) 2 = = 2 · 2 · ( x + 1 ) · ( x + 1 ) ‘ · ( x — 2 ) — ( x + 1 ) 2 · 1 ( x — 2 ) 2 = 2 · 2 · ( x + 1 ) · ( x — 2 ) — ( x + 2 ) 2 ( x — 2 ) 2 = = 2 · ( x + 1 ) · ( x — 5 ) ( x — 2 ) 2

Отсюда видим, что нули функции – это х = — 1 , х = 5 , х = 2 , то есть каждую скобку необходимо приравнять к нулю. Отметим на числовой оси и получим:

Теперь определим знаки производной из каждого интервала. Необходимо выбрать точку, входящую в интервал, подставить в выражение. Например, точки х = — 2 , х = 0 , х = 3 , х = 6 .

y ‘ ( — 2 ) = 2 · ( x + 1 ) · ( x — 5 ) ( x — 2 ) 2 x = — 2 = 2 · ( — 2 + 1 ) · ( — 2 — 5 ) ( — 2 — 2 ) 2 = 2 · 7 16 = 7 8 > 0 , значит, интервал — ∞ ; — 1 имеет положительную производную. Аналогичным образом получаем, что

y ‘ ( 0 ) = 2 · ( 0 + 1 ) · 0 — 5 0 — 2 2 = 2 · — 5 4 = — 5 2 0 y ‘ ( 3 ) = 2 · ( 3 + 1 ) · ( 3 — 5 ) ( 3 — 2 ) 2 = 2 · — 8 1 = — 16 0 y ‘ ( 6 ) = 2 · ( 6 + 1 ) · ( 6 — 5 ) ( 6 — 2 ) 2 = 2 · 7 16 = 7 8 > 0

Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.

Получим, что в точке х = — 1 функция будет непрерывна, значит, производная изменит знак с + на — . По первому признаку имеем, что х = — 1 является точкой максимума, значит получаем

y m a x = y ( — 1 ) = 2 · ( x + 1 ) 2 x — 2 x = — 1 = 2 · ( — 1 + 1 ) 2 — 1 — 2 = 0

Точка х = 5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид

y m i n = y ( 5 ) = 2 · ( x + 1 ) 2 x — 2 x = 5 = 2 · ( 5 + 1 ) 2 5 — 2 = 24

Ответ: y m a x = y ( — 1 ) = 0 , y m i n = y ( 5 ) = 24 .

Стоит обратить внимание на то, что использование первого достаточного признака экстремума не требует дифференцируемости функции с точке x 0 , этим и упрощает вычисление.

Найти точки максимума и минимума функции y = 1 6 x 3 = 2 x 2 + 22 3 x — 8 .

Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:

— 1 6 x 3 — 2 x 2 — 22 3 x — 8 , x 0 1 6 x 3 — 2 x 2 + 22 3 x — 8 , x ≥ 0

После чего необходимо найти производную:

y ‘ = 1 6 x 3 — 2 x 2 — 22 3 x — 8 ‘ , x 0 1 6 x 3 — 2 x 2 + 22 3 x — 8 ‘ , x > 0 y ‘ = — 1 2 x 2 — 4 x — 22 3 , x 0 1 2 x 2 — 4 x + 22 3 , x > 0

Точка х = 0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:

lim y ‘ x → 0 — 0 = lim y x → 0 — 0 — 1 2 x 2 — 4 x — 22 3 = — 1 2 · ( 0 — 0 ) 2 — 4 · ( 0 — 0 ) — 22 3 = — 22 3 lim y ‘ x → 0 + 0 = lim y x → 0 — 0 1 2 x 2 — 4 x + 22 3 = 1 2 · ( 0 + 0 ) 2 — 4 · ( 0 + 0 ) + 22 3 = + 22 3

Отсюда следует, что функция непрерывна в точке х = 0 , тогда вычисляем

lim y x → 0 — 0 = lim x → 0 — 0 — 1 6 x 3 — 2 x 2 — 22 3 x — 8 = = — 1 6 · ( 0 — 0 ) 3 — 2 · ( 0 — 0 ) 2 — 22 3 · ( 0 — 0 ) — 8 = — 8 lim y x → 0 + 0 = lim x → 0 — 0 1 6 x 3 — 2 x 2 + 22 3 x — 8 = = 1 6 · ( 0 + 0 ) 3 — 2 · ( 0 + 0 ) 2 + 22 3 · ( 0 + 0 ) — 8 = — 8 y ( 0 ) = 1 6 x 3 — 2 x 2 + 22 3 x — 8 x = 0 = 1 6 · 0 3 — 2 · 0 2 + 22 3 · 0 — 8 = — 8

Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:

— 1 2 x 2 — 4 x — 22 3 , x 0 D = ( — 4 ) 2 — 4 · — 1 2 · — 22 3 = 4 3 x 1 = 4 + 4 3 2 · — 1 2 = — 4 — 2 3 3 0 x 2 = 4 — 4 3 2 · — 1 2 = — 4 + 2 3 3 0

1 2 x 2 — 4 x + 22 3 , x > 0 D = ( — 4 ) 2 — 4 · 1 2 · 22 3 = 4 3 x 3 = 4 + 4 3 2 · 1 2 = 4 + 2 3 3 > 0 x 4 = 4 — 4 3 2 · 1 2 = 4 — 2 3 3 > 0

Все полученные точки нужно отметить на прямой для определения знака каждого интервала. Поэтому необходимо вычислить производную в произвольных точках у каждого интервала. Например, у нас можно взять точки со значениями x = — 6 , x = — 4 , x = — 1 , x = 1 , x = 4 , x = 6 . Получим, что

y ‘ ( — 6 ) = — 1 2 x 2 — 4 x — 22 3 x = — 6 = — 1 2 · — 6 2 — 4 · ( — 6 ) — 22 3 = — 4 3 0 y ‘ ( — 4 ) = — 1 2 x 2 — 4 x — 22 3 x = — 4 = — 1 2 · ( — 4 ) 2 — 4 · ( — 4 ) — 22 3 = 2 3 > 0 y ‘ ( — 1 ) = — 1 2 x 2 — 4 x — 22 3 x = — 1 = — 1 2 · ( — 1 ) 2 — 4 · ( — 1 ) — 22 3 = 23 6 0 y ‘ ( 1 ) = 1 2 x 2 — 4 x + 22 3 x = 1 = 1 2 · 1 2 — 4 · 1 + 22 3 = 23 6 > 0 y ‘ ( 4 ) = 1 2 x 2 — 4 x + 22 3 x = 4 = 1 2 · 4 2 — 4 · 4 + 22 3 = — 2 3 0 y ‘ ( 6 ) = 1 2 x 2 — 4 x + 22 3 x = 6 = 1 2 · 6 2 — 4 · 6 + 22 3 = 4 3 > 0

Изображение на прямой имеет вид

Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что

x = — 4 — 2 3 3 , x = 0 , x = 4 + 2 3 3 , тогда отсюда точки максимума имеют значени x = — 4 + 2 3 3 , x = 4 — 2 3 3

Перейдем к вычислению минимумов:

y m i n = y — 4 — 2 3 3 = 1 6 x 3 — 2 2 + 22 3 x — 8 x = — 4 — 2 3 3 = — 8 27 3 y m i n = y ( 0 ) = 1 6 x 3 — 2 2 + 22 3 x — 8 x = 0 = — 8 y m i n = y 4 + 2 3 3 = 1 6 x 3 — 2 2 + 22 3 x — 8 x = 4 + 2 3 3 = — 8 27 3

Произведем вычисления максимумов функции. Получим, что

y m a x = y — 4 + 2 3 3 = 1 6 x 3 — 2 2 + 22 3 x — 8 x = — 4 + 2 3 3 = 8 27 3 y m a x = y 4 — 2 3 3 = 1 6 x 3 — 2 2 + 22 3 x — 8 x = 4 — 2 3 3 = 8 27 3

y m i n = y — 4 — 2 3 3 = — 8 27 3 y m i n = y ( 0 ) = — 8 y m i n = y 4 + 2 3 3 = — 8 27 3 y m a x = y — 4 + 2 3 3 = 8 27 3 y m a x = y 4 — 2 3 3 = 8 27 3

Видео:Промежутки возрастания и убывания функции. Практическая часть. 10 класс.Скачать

Второй признак экстремума функции

Если задана функция f ‘ ( x 0 ) = 0 , тогда при ее f » ( x 0 ) > 0 получаем, что x 0 является точкой минимума, если f » ( x 0 ) 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .

Найти максимумы и минимумы функции y = 8 x x + 1 .

Для начала находим область определения. Получаем, что

D ( y ) : x ≥ 0 x ≠ — 1 ⇔ x ≥ 0

Необходимо продифференцировать функцию, после чего получим

y ‘ = 8 x x + 1 ‘ = 8 · x ‘ · ( x + 1 ) — x · ( x + 1 ) ‘ ( x + 1 ) 2 = = 8 · 1 2 x · ( x + 1 ) — x · 1 ( x + 1 ) 2 = 4 · x + 1 — 2 x ( x + 1 ) 2 · x = 4 · — x + 1 ( x + 1 ) 2 · x

При х = 1 производная становится равной нулю, значит, точка является возможным экстремумом. Для уточнения необходимо найти вторую производную и вычислить значение при х = 1 . Получаем:

y » = 4 · — x + 1 ( x + 1 ) 2 · x ‘ = = 4 · ( — x + 1 ) ‘ · ( x + 1 ) 2 · x — ( — x + 1 ) · x + 1 2 · x ‘ ( x + 1 ) 4 · x = = 4 · ( — 1 ) · ( x + 1 ) 2 · x — ( — x + 1 ) · x + 1 2 ‘ · x + ( x + 1 ) 2 · x ‘ ( x + 1 ) 4 · x = = 4 · — ( x + 1 ) 2 x — ( — x + 1 ) · 2 x + 1 ( x + 1 ) ‘ x + ( x + 1 ) 2 2 x ( x + 1 ) 4 · x = = — ( x + 1 ) 2 x — ( — x + 1 ) · x + 1 · 2 x + x + 1 2 x ( x + 1 ) 4 · x = = 2 · 3 x 2 — 6 x — 1 x + 1 3 · x 3 ⇒ y » ( 1 ) = 2 · 3 · 1 2 — 6 · 1 — 1 ( 1 + 1 ) 3 · ( 1 ) 3 = 2 · — 4 8 = — 1 0

Значит, использовав 2 достаточное условие экстремума, получаем, что х = 1 является точкой максимума. Иначе запись имеет вид y m a x = y ( 1 ) = 8 1 1 + 1 = 4 .

Ответ: y m a x = y ( 1 ) = 4 ..

Видео:Промежутки возрастания и убывания функции. Практическая часть. 10 класс.Скачать

Третье достаточное условие экстремума

Функция y = f ( x ) имеет ее производную до n -го порядка в ε окрестности заданной точки x 0 и производную до n + 1 -го порядка в точке x 0 . Тогда f ‘ ( x 0 ) = f » ( x 0 ) = f ‘ ‘ ‘ ( x 0 ) = . . . = f n ( x 0 ) = 0 .

Отсюда следует, что когда n является четным числом, то x 0 считается точкой перегиба, когда n является нечетным числом, то x 0 точка экстремума, причем f ( n + 1 ) ( x 0 ) > 0 , тогда x 0 является точкой минимума, f ( n + 1 ) ( x 0 ) 0 , тогда x 0 является точкой максимума.

Найти точки максимума и минимума функции y y = 1 16 ( x + 1 ) 3 ( x — 3 ) 4 .

Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что

y ‘ = 1 16 x + 1 3 ‘ ( x — 3 ) 4 + ( x + 1 ) 3 x — 3 4 ‘ = = 1 16 ( 3 ( x + 1 ) 2 ( x — 3 ) 4 + ( x + 1 ) 3 4 ( x — 3 ) 3 ) = = 1 16 ( x + 1 ) 2 ( x — 3 ) 3 ( 3 x — 9 + 4 x + 4 ) = 1 16 ( x + 1 ) 2 ( x — 3 ) 3 ( 7 x — 5 )

Данная производная обратится в ноль при x 1 = — 1 , x 2 = 5 7 , x 3 = 3 . То есть точки могут быть точками возможного экстремума. Необходимо применить третье достаточное условие экстремума. Нахождение второй производной позволяет в точности определить наличие максимума и минимума функции. Вычисление второй производной производится в точках ее возможного экстремума. Получаем, что

y » = 1 16 x + 1 2 ( x — 3 ) 3 ( 7 x — 5 ) ‘ = 1 8 ( x + 1 ) ( x — 3 ) 2 ( 21 x 2 — 30 x — 3 ) y » ( — 1 ) = 0 y » 5 7 = — 36864 2401 0 y » ( 3 ) = 0

Значит, что x 2 = 5 7 является точкой максимума. Применив 3 достаточный признак, получаем, что при n = 1 и f ( n + 1 ) 5 7 0 .

Необходимо определить характер точек x 1 = — 1 , x 3 = 3 . Для этого необходимо найти третью производную, вычислить значения в этих точках. Получаем, что

y ‘ ‘ ‘ = 1 8 ( x + 1 ) ( x — 3 ) 2 ( 21 x 2 — 30 x — 3 ) ‘ = = 1 8 ( x — 3 ) ( 105 x 3 — 225 x 2 — 45 x + 93 ) y ‘ ‘ ‘ ( — 1 ) = 96 ≠ 0 y ‘ ‘ ‘ ( 3 ) = 0

Значит, x 1 = — 1 является точкой перегиба функции, так как при n = 2 и f ( n + 1 ) ( — 1 ) ≠ 0 . Необходимо исследовать точку x 3 = 3 . Для этого находим 4 производную и производим вычисления в этой точке:

y ( 4 ) = 1 8 ( x — 3 ) ( 105 x 3 — 225 x 2 — 45 x + 93 ) ‘ = = 1 2 ( 105 x 3 — 405 x 2 + 315 x + 57 ) y ( 4 ) ( 3 ) = 96 > 0

Из выше решенного делаем вывод, что x 3 = 3 является точкой минимума функции.

Ответ: x 2 = 5 7 является точкой максимума, x 3 = 3 — точкой минимума заданной функции.

💡 Видео

Промежутки возрастания и убывания функции.Скачать

Урок 11. Возрастание и убывание функции. Алгебра 11 классСкачать