Уравнения на группировку 9 класс (5 видео)

Лекция по теме «Уравнения высших степеней. Методы их решения». 9-й класс

Разделы: Математика

Класс: 9

Закрепить понятие целого рационального уравнения -й степени.
Сформулировать основные методы решения уравнений высших степеней (n > 3).
Обучить основным методам решения уравнений высших степеней.
Научить по виду уравнения определять наиболее эффективный способ его решения.

Формы, методы и педагогические приемы, которые используются учителем на уроке:

Лекционно-семинарская система обучения (лекции – объяснение нового материала, семинары – решение задач).
Информационно-коммуникационные технологии (фронтальный опрос, устная работа с классом).
Дифференцированное обучение, групповые и индивидуальные формы.
Использование исследовательского метода в обучении, направленного на развитие математического аппарата и мыслительных способностей каждого конкретного ученика.
Печатный материал – индивидуальный краткий конспект урока (основные понятия, формулы, утверждения, материал лекций сжато в виде схем или таблиц).

Организационный момент.
Цель этапа: включить учащихся в учебную деятельность, определить содержательные рамки урока.
Актуализация знаний учащихся.
Цель этапа: актуализировать знания учащихся по изученным ранее смежным темам
Изучение новой темы (лекция). Цель этапа: сформулировать основные методы решения уравнений высших степеней (n > 3)
Подведение итогов.
Цель этапа: еще раз выделить ключевые моменты в материале, изученном на уроке.
Домашнее задание.
Цель этапа: сформулировать домашнее задание для учащихся.

1. Организационный момент.

Формулировка темы урока: “Уравнения высших степеней. Методы их решения”.

2. Актуализация знаний учащихся.

Теоретический опрос – беседа. Повторение некоторых ранее изученных сведений из теории. Учащиеся формулируют основные определения и дают формулировки необходимых теорем. Приводят примеры, демонстрируя уровень полученных ранее знаний.

Понятие уравнения с одной переменной.
Понятие корня уравнения, решения уравнения.
Понятие линейного уравнения с одной переменной, понятие квадратного уравнения с одной переменной.
Понятие равносильности уравнений, уравнения-следствия (понятие посторонних корней), переход не по следствию (случай потери корней).
Понятие целого рационального выражения с одной переменной.
Понятие целого рационального уравнения n-й степени. Стандартный вид целого рационального уравнения. Приведенное целое рациональное уравнение.
Переход к совокупности уравнений более низких степеней путем разложения исходного уравнения на множители.
Понятие многочлена n-й степени от x. Теорема Безу. Следствия из теоремы Безу. Теоремы о корнях (Z-корни и Q-корни) целого рационального уравнения с целыми коэффициентами (соответственно приведенного и неприведенного).
Схема Горнера.

3. Изучение новой темы.

Будем рассматривать целое рациональное уравнение n-й степени стандартного вида с одной неизвестной переменной x : P_n(x) = 0 , где P_n(x) = a_nx n + a_n-1x n-1 + a₁x + a₀ – многочлен n-й степени от x, a_n ≠ 0 . Если a_n = 1 то такое уравнение называют приведенным целым рациональным уравнением n-й степени. Рассмотрим такие уравнения при различных значениях n и перечислим основные методы их решения.

n = 1 – линейное уравнение.

n = 2 – квадратное уравнение. Формула дискриминанта. Формула для вычисления корней. Теорема Виета. Выделение полного квадрата.

n = 3 – кубическое уравнение.

Пример: x 3 – 4x 2 – x + 4 = 0 (x – 4)(x 2 – 1) = 0 x₁ = 4 , x₂ = 1, x₃ = -1.

Возвратное кубическое уравнение вида ax 3 + bx 2 + bx + a = 0. Решаем, объединяя члены с одинаковыми коэффициентами.

Пример: x 3 – 5x 2 – 5x + 1 = 0 (x + 1)(x 2 – 6x + 1) = 0 x₁ = -1, x₂ = 3 + 2, x₃ = 3 – 2.

Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы. Схема Горнера. При применении этого метода необходимо сделать акцент на том, что перебор в данном случае конечный, и корни мы подбираем по определенному алгоритму в соответствии с теоремой о Z-корнях приведенного целого рационального уравнения с целыми коэффициентами.

Пример: x 3 – 9x 2 + 23x – 15 = 0. Уравнение приведенное. Выпишем делители свободного члена <+1; +3; +5; +15>. Применим схему Горнера:

x 3	x 2	x 1	x 0	вывод
1	-9	23	-15
1	1	1 х 1 – 9 = -8	1 х (-8) + 23 = 15	1 х 15 – 15 = 0	1 – корень
x 2	x 1	x 0

Получаем (x – 1)(x 2 – 8x + 15) = 0 x₁ = 1, x₂ = 3, x₃ = 5.

Уравнение с целыми коэффициентами. Подбор Q-корней на основании теоремы. Схема Горнера. При применении этого метода необходимо сделать акцент на том, что перебор в данном случае конечный и корни мы подбираем по определенному алгоритму в соответствии с теоремой о Q-корнях неприведенного целого рационального уравнения с целыми коэффициентами.

Пример: 9x 3 + 27x 2 – x – 3 = 0. Уравнение неприведенное. Выпишем делители свободного члена <+1; +3>. Выпишем делители коэффициента при старшей степени неизвестного. <+1; +3; +9> Следовательно, корни будем искать среди значений <+1; +; +; +3>. Применим схему Горнера:

x 3	x 2	x 1	x 0	вывод
9	27	-1	-3
1	9	1 x 9 + 27 = 36	1 x 36 – 1 = 35	1 x 35 – 3 = 32 ≠ 0	1 – не корень
-1	9	-1 x 9 + 27 = 18	-1 x 18 – 1 = -19	-1 x (-19) – 3 = 16 ≠ 0	-1 – не корень
	9	x 9 + 27 = 30	x 30 – 1 = 9	x 9 – 3 = 0	корень
x 2	x 1	x 0

Получаем (x – )(9x 2 + 30x + 9) = 0 x₁ = , x₂ = — , x₃ = -3.

Для удобства подсчета при подборе Q-корней бывает удобно сделать замену переменной, перейти к приведенному уравнению и подбирать Z-корни.

Если можно воспользоваться заменой вида y = kx.

Формула Кардано. Существует универсальный метод решения кубических уравнений – это формула Кардано. Эту формулу связывают с именами итальянских математиков Джероламо Кардано (1501–1576), Николо Тарталья (1500–1557), Сципиона дель Ферро (1465–1526). Эта формула лежит за рамками нашего курса.

n = 4 – уравнение четвертой степени.

Пример: x 4 + 2x 3 + 5x 2 + 4x – 12 = 0 (x 4 + 2x 3 ) + (5x 2 + 10x) – (6x + 12 ) = 0 (x + 2)(x 3 + 5x – 6) = 0 (x + 2)(x – 1)(x 2 + x + 6) = 0 x₁ = -2, x₂ = 1.

Метод замены переменной.

Возвратное уравнение четвертой степени вида ax 4 + bx 3 + cx 2 + bx + a = 0.

Решаем, объединяя члены с одинаковыми коэффициентами, путем замены вида

Обобщенное возвратное уравнение четвертой степени вида ax 4 + bx 3 + cx 2 – bx + a = 0.

Обобщенное возвратное уравнение четвертой степени вида ax 4 + bx 3 + cx 2 + kbx + k 2 a = 0.

Замена общего вида. Некоторые стандартные замены.

Пример 3. Замена общего вида (вытекает из вида конкретного уравнения).

Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.

Уравнение с целыми коэффициентами. Подбор Q-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.

Формула общего вида. Существует универсальный метод решения уравнений четвертой степени. Эту формулу связывают с именем Людовико Феррари (1522–1565). Эта формула лежит за рамками нашего курса.

n > 5 – уравнения пятой и более высоких степеней.

Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.

Симметрические уравнения. Любое возвратное уравнение нечетной степени имеет корень x = -1 и после разложения его на множители получаем, что один сомножитель имеет вид (x + 1), а второй сомножитель – возвратное уравнение четной степени (его степень на единицу меньше, чем степень исходного уравнения). Любое возвратное уравнение четной степени вместе с корнем вида x = φ содержит и корень вида . Используя эти утверждения, решаем задачу, понижая степень исследуемого уравнения.

Метод замены переменной. Использование однородности.

Не существует формулы общего вида для решения целых уравнений пятой степени (это показали итальянский математик Паоло Руффини (1765–1822) и норвежский математик Нильс Хенрик Абель (1802–1829)) и более высоких степеней (это показал французский математик Эварист Галуа (1811–1832)).

Напомним еще раз, что на практике возможно использование комбинации перечисленных выше методов. Удобно переходить к совокупности уравнений более низких степеней путем разложения исходного уравнения на множители.
За рамками нашего сегодняшнего обсуждения остались широко используемые на практике графические методы решения уравнений и методы приближенного решения уравнений высших степеней.
Бывают ситуации, когда у уравнения нет R-корней. Тогда решение сводится к тому, чтобы показать, что уравнение корней не имеет. Для доказательства анализируем поведение рассматриваемых функций на промежутках монотонности. Пример: уравнение x 8 – x 3 + 1 = 0 не имеет корней.
Использование свойства монотонности функций. Бывают ситуации, когда использование различных свойств функций позволяет упростить поставленную задачу.
Пример 1: уравнение x 5 + 3x – 4 = 0 имеет один корень x = 1. По свойству монотонности анализируемых функций других корней нет.
Пример 2: уравнение x 4 + (x – 1) 4 = 97 имеет корни x₁ = -2 и x₂ = 3. Проанализировав поведение соответствующих функций на промежутках монотонности, заключаем, что других корней нет.

4. Подведение итогов.

Резюме: Теперь мы овладели основными методами решения различных уравнений высших степеней (для n > 3). Наша задача научиться эффективно использовать перечисленные выше алгоритмы. В зависимости от вида уравнения мы должны будем научиться определять, какой способ решения в данном случае является наиболее эффективным, а также правильно применять выбранный метод.

5. Домашнее задание.

[1]: п.7, стр. 164–174, №№ 33–36, 39–44, 46,47.

[4]: №№ 9.1–9.4, 9.6–9.8, 9.12, 9.14–9.16, 9.24–9.27.

Возможные темы докладов или рефератов по данной тематике:

Формула Кардано
Графический метод решения уравнений. Примеры решения.
Методы приближенного решения уравнений.

Анализ усвоения материала и интереса учащихся к теме:

Опыт показывает, что интерес учащихся в первую очередь вызывает возможность подбора Z-корней и Q-корней уравнений при помощи достаточно простого алгоритма с использованием схемы Горнера. Также учащиеся интересуются различными стандартными типами замены переменных, которые позволяют существенно упрощать вид задачи. Особый интерес обычно вызывают графические методы решения. В этом случае дополнительно можно разобрать задачи на графический метод решения уравнений; обсудить общий вид графика для многочлена 3, 4, 5 степени; проанализировать, как связано число корней уравнений 3, 4, 5 степени с видом соответствующего графика. Ниже приведен список книг, в которых можно найти дополнительную информацию по данной тематике.

Виленкин Н.Я. и др. “Алгебра. Учебник для учащихся 9 классов с углубленным изучением математики” – М., Просвещение, 2007 – 367 с.
Виленкин Н.Я., Шибасов Л.П., Шибасова З.Ф. “За страницами учебника математики. Арифметика. Алгебра. 10-11 класс” – М., Просвещение, 2008 – 192 с.
Выгодский М.Я. “Справочник по математике” – М., АСТ, 2010 – 1055 с.
Галицкий М.Л. “Сборник задач по алгебре. Учебное пособие для 8-9 классов с углубленным изучением математики” – М., Просвещение, 2008 – 301 с.
Звавич Л.И. и др. “Алгебра и начала анализа. 8–11 кл. Пособие для школ и классов с углубленным изучением математики” – М., Дрофа, 1999 – 352 с.
Звавич Л.И., Аверьянов Д.И., Пигарев Б.П., Трушанина Т.Н. “Задания по математике для подготовки к письменному экзамену в 9 классе” – М., Просвещение, 2007 – 112 с.
Иванов А.А., Иванов А.П. “Тематические тесты для систематизации знаний по математике” ч.1 – М., Физматкнига, 2006 – 176 с.
Иванов А.А., Иванов А.П. “Тематические тесты для систематизации знаний по математике” ч.2 – М., Физматкнига, 2006 – 176 с.
Иванов А.П. “Тесты и контрольные работы по математике. Учебное пособие”. – М., Физматкнига, 2008 – 304 с.
Лейбсон К.Л. “Сборник практических заданий по математике. Часть 2–9 класс” – М., МЦНМО, 2009 – 184 с.
Макарычев Ю.Н., Миндюк Н.Г. “Алгебра. Дополнительные главы к школьному учебнику 9 класса. Учебное пособие для учащихся школ и классов с углубленным изучением математики.” – М., Просвещение, 2006 – 224 с.
Мордкович А.Г. “Алгебра. Углубленное изучение. 8 класс. Учебник” – М., Мнемозина, 2006 – 296 с.
Савин А.П. “Энциклопедический словарь юного математика” – М., Педагогика, 1985 – 352 с.
Сурвилло Г.С., Симонов А.С. “Дидактические материалы по алгебре для 9 класса с углубленным изучением математики” – М., Просвещение, 2006 – 95 с.
Чулков П.В. “Уравнения и неравенства в школьном курсе математик. Лекции 1–4” – М., Первое сентября, 2006 – 88 с.
Чулков П.В. “Уравнения и неравенства в школьном курсе математик. Лекции 5–8” – М., Первое сентября, 2009 – 84 с.

Содержание

Презентация по алгебре»способ группировки»
Выберите документ из архива для просмотра:
Описание презентации по отдельным слайдам:
Решение уравнения методами группировки и замены переменной
Страницы работы
Содержание работы
📹 Видео

Видео:Задание №1 "Решите методом группировки" по теме "Целое уравнение и его корни". Алгебра 9 классСкачать

Презентация по алгебре»способ группировки»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Приложение 1.ppt

Описание презентации по отдельным слайдам:

Учитель математики Наталья Игоревна Касьянова МБОУ гимназия №5 г. Морозовск Ростовской обл.

УСТНО Что значит разложить многочлен на множители? Какие способы разложения многочлена на множители вы знаете? Сформулируйте алгоритм разложения многочлена на множители способом вынесения общего множителя за скобки.

УСТНО Вынести за скобки общий множитель: 1) 6а+9х; 2) ay–ax; 3) a2 –a³b; 4) 16mn – 4mn3 ; 5) 12(a+b) –x(a+b).

«Вынесение общего множителя за скобки»

Вынеси общий множитель за скобки: 15х + 10y; a2 – ab; n(7-m) + k(7–m); 8m2n – 4mn3 ; a(b-c)+3(c-b). 9n + 6m; b² — ab; b(a+5) – c(a+5); 20x³y² + 4x²y³; 6(m-n)+s(n-m).

ПРОВЕРКА 5(3х +2у); a(a-b); (7-m)(n+k); 4mn(2m-n²); (b-c)(a+3). 3(3n + 2m); b(b – a); (a+5)(b-c); 4xy(5x + y); (6–s)(m-n). 5 – «5»; 4 – «4»; 3 – «3».

РЕШИТЕ УРАВНЕНИЕ 1) x (x-11) = 0; 2) 6x² – 2x = 0; 3) x2 + 3x + 6 + 2x = 0. — Есть ли общий множитель у всех слагаемых? — Значит способ разложения на множители не подходит.

x2 + 3x + 6 + 2x = 0. РЕШЕНИЕ: Пристально посмотрим на левую часть уравнения…Что-нибудь вы видите? Попробуем объединить в группы: (x2 + 3x) + (6 + 2x) = 0; Теперь у одночленов в скобках появились общие множители х(x + 3) + 2(3 + x) = 0; (х + 3)(х +2) = 0;

Способ группировки Данный способ применяют к многочленам, которые не имеют общего множителя для всех членов многочлена. Чтобы разложить многочлен на множители способом группировки, нужно: Объединить члены многочлена в такие группы, которые имеют общий множитель в виде многочлена. Вынести этот общий множитель за скобки.

ПРИМЕР Разложить на множители многочлен: xy-6+3х-2y Первый способ группировки: xy-6+3х-2y=(xy-6)+(3x-2y).(Группировка неудачна.) Второй способ группировки: xy-6+3х-2y=(xy+3x)+(-6-2y)= =x(y+3)-2(y+3)=(y+3)(x-2). Третий способ группировки: xy-6+3х-2y=(xy-2y)+(-6+3x)= =y(x-2)+3(x-2)=(x-2)(y+3). Ответ: xy-6+3х-2y=(x-2)(y+3). Как видите, не всегда с первого раза группировка оказывается удачной. Если группировка оказалась неудачной, откажитесь от нее и ищите иной способ.

РАЗЛОЖИТЕ НА МНОЖИТЕЛИ: ах + 3х + 4а + 12; аb — 8а – bх + 8х; x2m — x2n + y2m — y2n.

Дифференцированные задания по уровням А. Задания нормативного уровня. 1) 7а — 7в + аn – bn 2) xy + 2y + 2x + 4 3) y2a — y2b + x2a — x2b Б. Задания компетентного уровня 1) xy + 2y — 2x – 4 2) 2сх – су – 6х + 3у 3) х2 + xy + xy2 + y3 С. Задания творческого уровня 1) x4 + x3y — xy3 — y4 2) ху2 – ву2 – ах + ав + у2 – а 3) х2 – 5х + 6

ДОМАШНЕЕ ЗАДАНИЕ § 32 (алгоритм знать); № 32.3(а); № 32.4 (а).

ИТОГ УРОКА а) С каким новым способом разложения многочлена на множители вы познакомились сегодня? б) В чем он заключается? в) К каким многочленам обычно применяют способ группировки?

БЛАГОДАРЮ ЗА УРОК!

Выбранный для просмотра документ Статья.docx

ТЕМА: РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ.

Тема «Разложение многочленов на множители» имеет большое значение и занимает значительное место в курсе алгебры 7 класса.

Во-первых, учащимся учитель объясняет, как с помощью разложения многочлена на множители можно упростить запись многочлена или облегчить вычисление числового значения выражения.

Во-вторых, в дальнейшем разложение на множители будет использоваться на протяжении всего курса алгебры: при выполнении действий над алгебраическими дробями — сокращении, сложении и вычитании, умножении и делении, а также при решении уравнений и неравенств и др.

Задача о разложении многочлена на множители является достаточно сложной. Это можно объяснить отсутствием четкого алгоритма разложения многочленов на множители, часто приходится догадываться, какой из способов разложения можно применить в каждом конкретном случае. Учитывая эти факты, становится ясно, насколько серьезная задача стоит перед учителем: сформировать у всех учащихся (включая учащихся со специальными потребностями) навыки в разложении на множители сначала на простых упражнениях, а для сильных учащихся на протяжении всего года и далее до конца курса рассмотреть более сложные случаи.

Основные характеристики урока:

Урок алгебры в 7 классе.

Технологии обучения: личностно – ориентированная, информационно – коммуникационная, проблемного обучения.

Продолжительность: 45 минут.

Автор: Касьянова Наталья Игоревна, учитель математики, МБОУ гимназия №5, г. Морозовск, Ростовская область.

При изучении темы «Разложение многочлена на множители способом группировки» ставятся следующие цели:

1) выработать у учащихся умения выполнять разложение многочленов на множители способом группировки,

2) выработать у учащихся умения применять полученные знания для рационализации вычислений, решения уравнений, доказательства тождеств.

1) формирование алгоритмического мышления;

2) формирование у учащихся навыков умственного труда — планирование своей работы, поиск рациональных путей ее выполнения, критическую оценку результатов;

1) эстетическое воспитание учащихся;

2) формирование представлений о математике как части общечеловеческой культуры.

Тип урока: изучение нового материала, проблемный.

Методы обучения: проблемный, частично-поисковый.

Форма организации учебной деятельности: групповая, фронтальная, индивидуальная.

Оборудование: персональный компьютер, мультимедийный проектор, экран, Презентация Power Point (Приложение 1).

Актуализация опорных знаний: ответы на устные вопросы и устные задания по теме «Вынесение общего множителя за скобки»; математический диктант с дальнейшей проверкой (слайды № 2-6).

Мотивирование необходимости разложения многочлена на множители — решение уравнений слайда № 8 и создание проблемной ситуации (уравнение № 3 не решается известным способом «вынесения общего множителя за скобки»). Постановка учебной задачи: научиться раскладывать многочлен на множители другим способом.

Совместное решение проблемы (слайд № 9), формулирование алгоритма разложения многочлена на множители способом группировки (слайд № 10) и рассмотрение примера на применение данного алгоритма несколькими способами (слайд № 11).

Применение полученных знаний при решении упражнений – работа у доски и с места (слайд № 12).

Дифференцированные задания по уровням – учащиеся выбирают один из вариантов, который соответствует их уровню знаний (слайд № 13).

Итог урока и домашнее задание (слайды № 14-16).

Список используемой литературы:

Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. – М.: Мнемозина, 2009.

Алгебра. 7 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович. – М.: Мнемозина, 2009.

Алгебра. 7 класс. Самостоятельные работы для учащихся общеобразовательных учреждений / Л. А. Александрова; под ред. А. Г. Мордковича. – М.: Мнемозина, 2009.

Алгебра. 7 класс. Контрольные работы для учащихся общеобразовательных учреждений / Л. А. Александрова; под ред. А. Г. Мордковича. – М.: Мнемозина, 2009.

Видео:Что такое Метод Группировки? Для Чайников, Урок 11Скачать

Решение уравнения методами группировки и замены переменной

Страницы работы

Содержание работы

Лабораторная работа №1

Цель работы: Решить уравнения методами:

б) замены переменной.

Теоретическая часть работы

Способ группировки разложение на множители

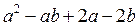
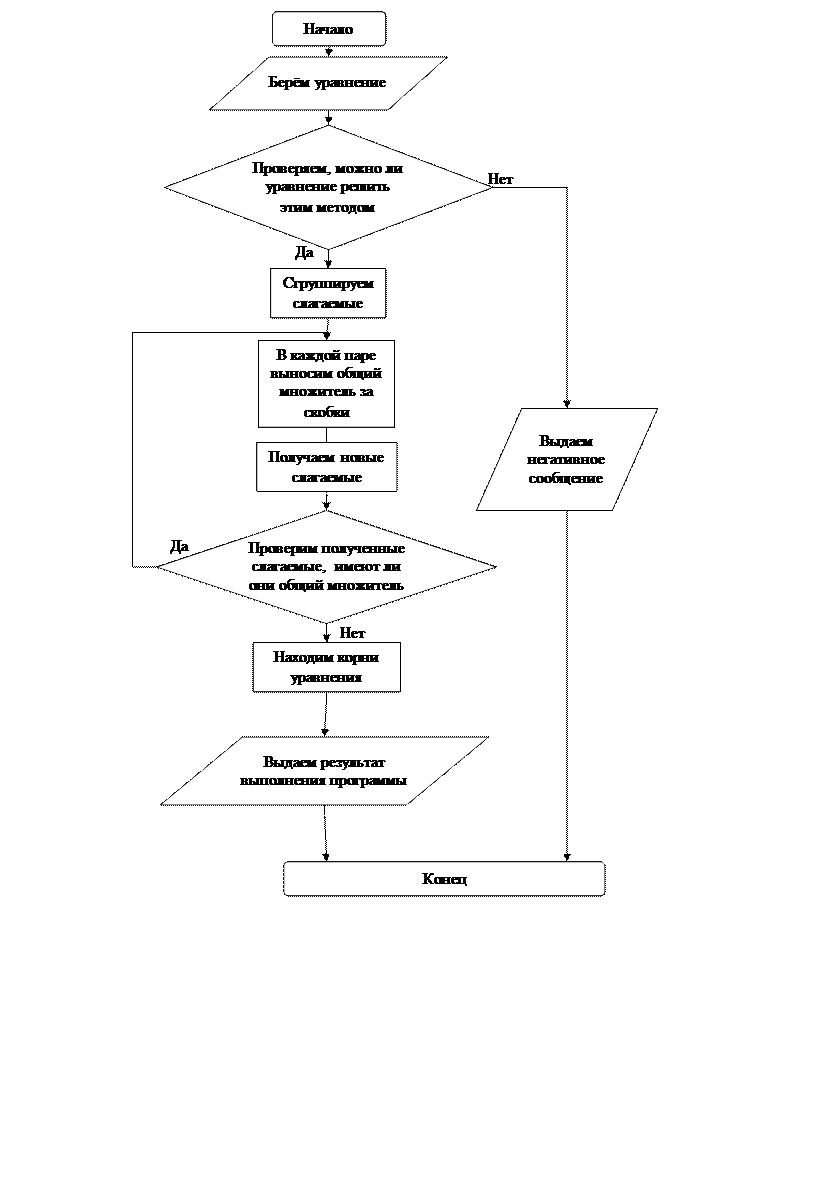
Для того, чтобы разложить многочлен на множители:

1 – Объединим слагаемые попарно в группы (говорят «сгруппируем слагаемые»): два в одну группу, и два — в другую .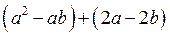

2 – В каждой паре вынесем за скобки общий множитель.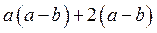

3 – Заметим, что оба полученных слагаемых также имеют общий множитель, который можно вынести за скобки .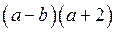

Не любая группировка приводит к разложению на множители. В случае неудачи попробуйте сгруппировать по-другому, или вообще попытайтесь применить другой метод.

Рассмотрим решение уравнения способом разложения на множители на конкретном примере:

Применив способ группировки, получим:

Помня, что произведение равно 0 в случае, если один из множителей равен 0, получим корни уравнения:

Метод введения новой переменной

Пример.

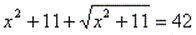
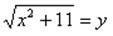
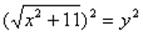
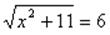
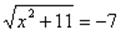
Введем новую переменную , учитывая, что , получаем квадратное уравнение у 2 +у – 42=0 , корни которого -7 и 6. Возвращаясь к переменной х, получаем уравнения и , последнее не имеет корней, т.к. арифметический квадратный корень – неотрицательное число, а первое уравнение можно решить, используя определение арифметического квадратного корня 6 2 = х 2 +11 , решение которого х=5 и х=-5.

Если уравнение можно свести к уравнению, содержащему два или несколько одинаковых выражений, то это уравнение можно решить методом замены переменной. Для этого заменяют такое выражение другой переменной, получают новое уравнение относительно новой переменной, решают его, затем осуществляют обратную замену, возвращаясь к прежней переменной.

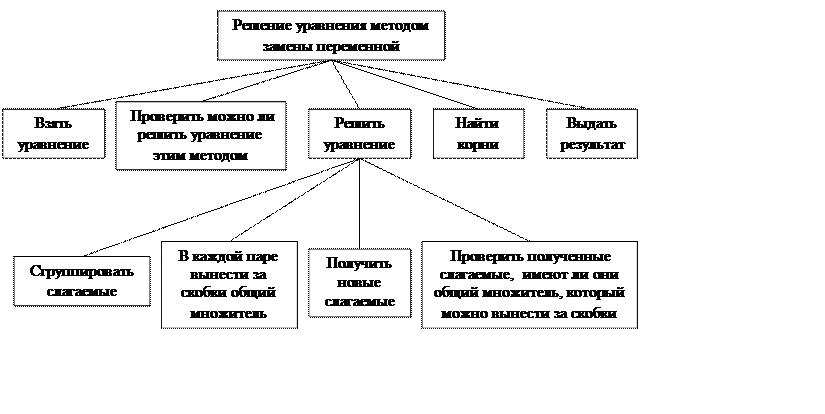
Структурная схема программы: а) способ группировки разложение на множители