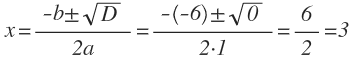Уравнения на дискриминант 8 класс задания

Видео:Решение квадратных уравнений. Дискриминант. Практическая часть. 1ч. 8 класс.Скачать

Тренировочные задания на решение квадратных уравнений 8 класс

Квадратные уравнения 8 класс алгебра

Учитель: Федулкина Т.А.

• Что такое квадратные уравнения. Виды уравнений.

Формула квадратного уравнения: ax 2 +bx+c=0,где a≠0, где x — переменная, a,b,c — числовые коэффициенты.

Пример полного квадратного уравнения:

3x 2 -3x+2=0
x 2 -16x+64=0

Решение полных квадратных уравнений сводится к нахождению дискриминанта:

Формула дискриминанта: D=b 2 -4aс

Если D>0, то уравнение имеет два корня и находим эти корни по формуле:

Если D=0, уравнение имеет один корень

Если D 2 -x-6=0

Записываем сначала, чему равны числовые коэффициенты a, b и c.

Коэффициент a всегда стоит перед x 2 , коэффициент b всегда перед переменной x, а коэффициент c – это свободный член.
a=1,b=-1,c=-6
D=b 2 -4ac=(-1) 2 -4∙1∙(-6)=1+24=25

Дискриминант больше нуля, следовательно, у нас два корня, найдем их:

№2 x 2 +2x+1=0
Записываем, чему равны числовые коэффициенты a,b и c.
a=1,b=2,c=1
D=b 2 -4ac=(2) 2 -4∙1∙1=4-4=0
Дискриминант равен нулю, следовательно, один корень:
x=-b/2a=-2/(2∙1)=-1

№3 7x 2 -x+2=0
Записываем, чему равны числовые коэффициенты a,b и c.
a=7,b=-1,c=2
D=b 2 -4ac=(-1) 2 -4∙7∙2=1-56=-55
Дискриминант меньше нуля, следовательно, корней нет.

Рассмотрим неполное квадратное уравнение:
ax 2 +bx=0, где числовой коэффициент c=0.

Пример как выглядят такие уравнения: x 2 -8x=0, 5x 2 +4x=0.

Чтобы решить такое уравнение необходимо переменную x вынести за скобки. А потом каждый множитель приравнять к нулю и решить уже простые уравнения.
ax 2 +bx=0 x(ax+b)=0 x₁=0 x₂=-b/a

№1 3x 2 +6x=0
Выносим переменную x за скобку,
x(3x+6)=0
Приравниваем каждый множитель к нулю,
x₁=0 3x+6=0 3x=-6 x₂=-2

№2 x 2 -x=0
Выносим переменную x за скобку,
x(x-1)=0
Приравниваем каждый множитель к нулю,
x₁=0
x₂=1

Рассмотрим неполное квадратное уравнение:
ax 2 +c=0, где числовой коэффициент b=0.

Чтобы решить это уравнение, нужно записать так:
x 2 =c/a , если число c/a будет отрицательным числом, то уравнение не имеет решения.
А если c/a положительное число, то решение выглядит таким образом: корень квадратного уравнения

№1 x 2 +5=0
x 2 =-5, видно, что -5 2 -12=0
3x 2 =12
x 2 =12/3
x 2 =4
x₁=2

2) Тренировочные задания на решение квадратных уравнений 8 класс алгебра.

Задания для устного решения:

1. Решите неполное квадратное уравнение:

Видео:Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать

Как найти дискриминант квадратного уравнения

О чем эта статья:

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, содержащее переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим:

13 = 12 — противоречие.

Значит, х = 5 не является корнем уравнения.

Если же х = 4, то при подстановке в уравнение мы получим:

12 = 12 — верное равенство.

Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.

Такое уравнение можно решить с помощью формулы дискриминанта.

Видео:Алгебра 8 класс (Урок№29 - Решение задач с помощью квадратных уравнений.)Скачать

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Как решать квадратные уравнения через дискриминант

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

Определим, чему равны коэффициенты a, b, c.

Вычислим значение дискриминанта по формуле D = b2 − 4ac.

Если дискриминант D 0, то у уравнения две корня, равные

Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:

Видео:Квадратичная функция и ее график. 8 класс.Скачать

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3x 2 — 4x + 2 = 0.

1. Определим коэффициенты: a = 3, b = -4, c = 2.
2. Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 3 * 2 = 16 — 24 = -8.

Ответ: D 2 — 6x + 9 = 0.

1. Определим коэффициенты: a = 1, b = -6, c = 9.
2. Найдем дискриминант: D = b 2 — 4ac = (-6) 2 — 4 * 1 * 9 = 36 — 36 = 0.

D = 0, значит уравнение имеет один корень:

Ответ: корень уравнения 3.

Пример 3. Решить уравнение: x 2 — 4x — 5 = 0.

1. Определим коэффициенты: a = 1, b = -4, c = -5.
2. Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 1 * (-5) = 16 + 20 = 36.

D > 0, значит уравнение имеет два корня:

Ответ: два корня x₁ = 5, x₂ = -1.

Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Уравнения на дискриминант 8 класс задания

Найдите корни уравнения .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решите уравнение .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

По теореме, обратной теореме Виета, сумма корней равна 1, а их произведение −6.

Тем самым, это числа −2 и 3.

Решите уравнение .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Запишем уравнение в виде По теореме, обратной теореме Виета, сумма корней равна −3, а их произведение −4.

🔍 Видео

Решение биквадратных уравнений. 8 класс.Скачать

Как решают уравнения в России и СШАСкачать

Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

Все про уравнения для задания 9 на ОГЭ 2024 по математикеСкачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

КВАДРАТНОЕ УРАВНЕНИЕ дискриминантСкачать

Алгебра 8. Урок 12 - Задачи на составление дробно-рациональных уравнений (Часть 1)Скачать

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Решение задач с помощью рациональных уравнений. Алгебра, 8 классСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Дробно-рациональные уравнения. 8 класс.Скачать

Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать