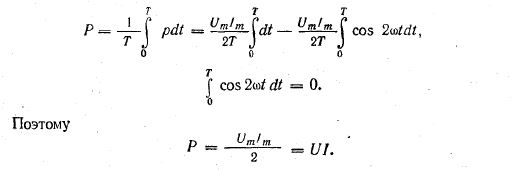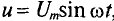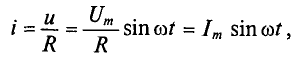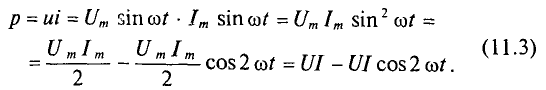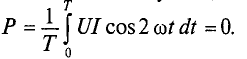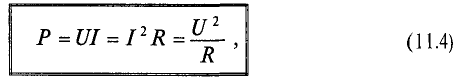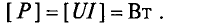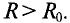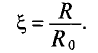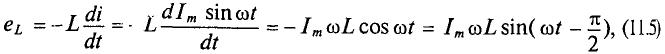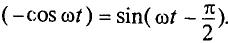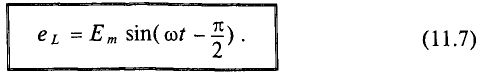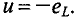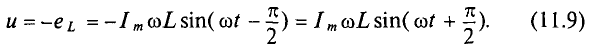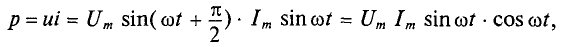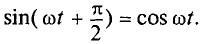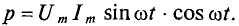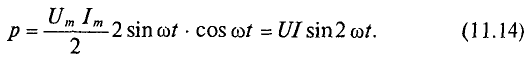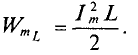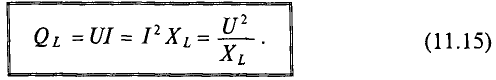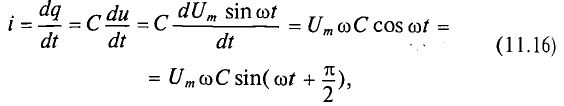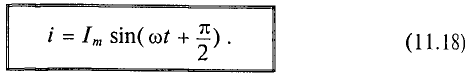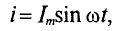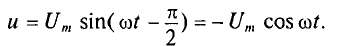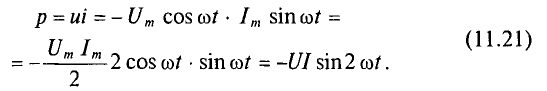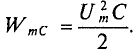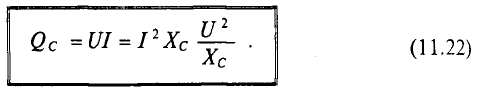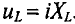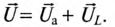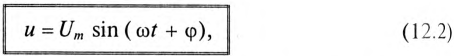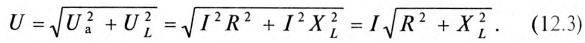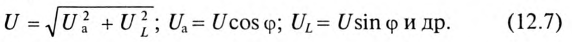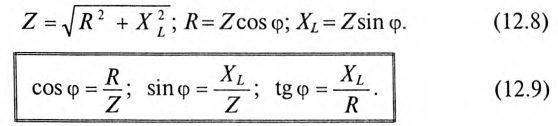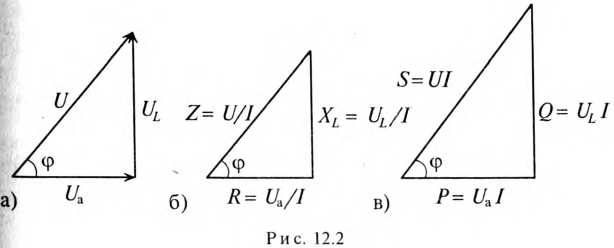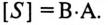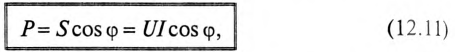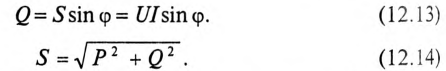Уравнения мгновенных значений тока и напряжения в цепи с активным сопротивлением

Электрические лампы накаливания, печи сопротивления, бытовые нагревательные приборы, реостаты и другие приемники, где электрическая энергия преобразуется в тепловую, на схемах замещения обычно представлены только сопротивлением R.
Для схемы, изображенной на рис. 13.1, а, заданы сопротивление R и напряжение, изменяющееся по закону

u = U_msinωt

Найдём ток и мощность в цепи.

Видео:Урок 358. Активное сопротивление в цепи переменного тока. Действующее значение тока и напряженияСкачать

Ток в цепи переменного тока с активным сопротивлением.

По закону Ома найдем выражение для мгновенного тока:

где I_m = U_m/R — амплитуда тока

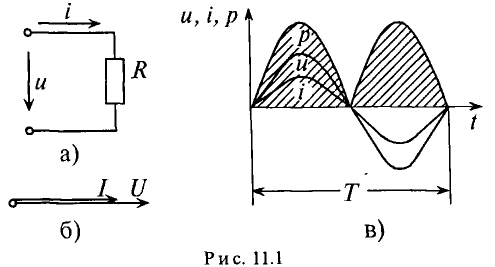
Из уравнений напряжения и тока видно, что начальные фазы обеих кривых одинаковы, т. е. напряжение и ток в цепи с сопротивлением R совпадают по фазе. Это показано на графиках и векторной диаграмме (рис. 13.1, б, б).

Действующий ток найдем, разделив амплитуду на √ 2:

Формулы (13.1) выражают закон Ома для цепи переменного тока с сопротивлением R. Внешне они ничем не отличаются от формулы для цепи постоянного тока, если переменные напряжение и ток выражены действующими величинами.

Видео:Цепи переменного тока. Комплексные значения сопротивлений, токов и напряжений в цепи. Задача 1Скачать

Мгновенная мощность в цепи переменного тока с активным сопротивлением.

При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p = U_msinωt * I_msinωt = U_mI_msin 2 ωt

Из тригонометрии найдём

Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = P_m√2 = U_mI_m√2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:

Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р = UmIm√2 и перемен- ной р’:

р = Р + р’

Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.

Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.

Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.

Видео:Активное и реактивное сопротивление в цепи переменного тока. 11 класс.Скачать

Активная мощность для цепи переменного тока с активным сопротивлением

Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.

Активная мощность — среднее арифметическое мгновенной мощности за период.

Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2. Средняя величина мощности равна высоте прямоугольника с основанием Т, равновеликого площади, ограниченной кривой р(t) и осью абсцисс (на рисунке заштриховано).

Равенство площадей РТ = S_p выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности P_m.

В этом случае часть площади Sp , находящаяся выше прямоугольника, точно укладывается в оставшуюся незаштрихованной его часть:

P = UI

Активная мощность для данной цепи равна произведению действующих величин тока и напряжения:

P = UI = I 2 R

С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности p(t) [см. выражение (13.2)].

Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода:

Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.

Видео:Урок 359. Конденсатор и катушка индуктивности в цепи переменного тока.Скачать

Электрические цепи синусоидального тока

Содержание:

Видео:Последовательное соединение RLC элементов в цепи синусоидального токаСкачать

Электрические цепи синусоидального тока:

В общем случае цепь переменного тока характеризуется тремя параметрами: активным сопротивлением R, индуктивностью L и емкостью С. В технике часто применяются цепи переменного тока, в которых преобладает один или два из этих параметров.

При анализе работы и расчетах цепей исходят из того, что для мгновенных значений переменного тока можно использовать все правила и законы постоянного тока.

Видео:Активное, индуктивное и емкостное сопротивления в цепи переменного токаСкачать

Цепь с активным сопротивлением

Активным сопротивлением R обладают элементы, которые нагреваются при прохождении через них тока (проводники, лампы накаливания, нагревательные приборы и т.д.).

Если к активному сопротивлению R (рис. 11.1) приложено синусоидальное напряжение

где

Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, так как начальные фазы их равны ( 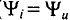= 0). Векторная диаграмма для цепи с активным сопротивлением изображена на рис. 11.16, временная диаграмма изображена на рис. 11.1в.

Математическое выражение закона Ома для цепи переменного тока с активным сопротивлением имеет вид:

Это вытекает из выражения (11.1), если левую и правую части уравнения разделить на 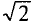=1,41.

Таким образом, действующее значение синусоидального тока I пропорционально действующему значению синусоидального напряжения U и обратно пропорционально сопротивлению R участка цепи, к которому приложено напряжение U. Такая интерпретация закона Ома справедлива как для мгновенных, так и для действующих и амплитудных значений синусоидального тока.

Активная мощность

Мгновенная мощность в цепи с активным сопротивлением определяется произведением мгновенных значений напряжения ка, т. е. р = ui. Это действие производится над кривыми тока и ряжения в определенном масштабе (рис. 11.1в). В результате учена временная диаграмма мгновенной мощности р. Как видно из временной диаграммы, мощность в цепи с активным сопротивлением изменяется по величине, но не изменяется по направлению (рис. 11.1в). Эта мощность (энергия) необратима. От источника она поступает на потребитель и полностью преобразуется в другие виды мощности (энергии), т.е. потребляется. Такая потребляемая мощность называется активной.

Поэтому и сопротивление R, на котором происходит подобное образование, называется активным сопротивлением, цепи с активным сопротивлением мгновенная мощность характеризует скорость преобразования электрической энергии в другие виды энергии.

Количественно мощность в цепи с активным сопротивлением определяется следующим образом:

Мгновенная мощность в цепи синусоидального тока с активным сопротивлением представляет собой сумму двух величин -постоянной мощности UI и переменной 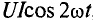, изменяющейся с двойной частотой.

Средняя за период мощность, равная постоянной составляющей мгновенной мощности UI, является активной мощностью Р. Среднее за период значение переменной составляющей, как и всякой синусоидальной величины, равно нулю, то есть

Таким образом, величина активной мощности в цепи синусоидального тока с активным сопротивлением с учетом закона Ома определяется выражением:

где U- действующее значение напряжения; I— действующее значение тока.

Единицей активной мощности является ватт:

Поверхностный эффект и эффект близости

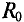
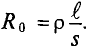
Сопротивление проводника постоянному току называют омическим сопротивлением и определяют выражением (2.8) Сопротивление проводника переменному току R называют активным.

Оказывается, что сопротивление проводника переменному току больше его омического сопротивления за счет так называемого поверхностного эффекта и эффекта близости, т. е.

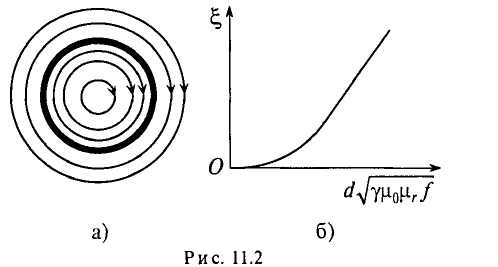
Увеличение активного сопротивления вызвано неодинаковой плотностью тока в различных сечениях проводника (рис. 11.2а).

На рис. 11.2а изображено магнитное поле проводника цилиндрического сечения. Если по проводнику проходит переменный ток, то он создает переменный магнитный поток внутри и вне проводника. Этот поток в различных сечениях проводника индуктирует ЭДС самоиндукции, которая, согласно правилу Ленца. противодействует изменению тока как причине создания ЭДС Очевидно, центр проводника охвачен большим количеством магнитных линий (большее потокосцепление), чем слои, близкие к поверхности. Следовательно, в центре проводника ЭДС (сопротивление) больше, чем на поверхности проводника. Плотность на поверхности больше, чем в центре. Поэтому это явление и называется поверхностным эффектом.

Таким образом, поверхностный эффект уменьшает сечение проводника для переменного тока, а следовательно, увеличивает активное сопротивление R.

Отношение активного сопротивления проводника к его сопротивлению определяет коэффициент поверхностного эффекта 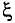(кси)

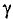
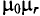
График зависимости коэффициента поверхностного эффекта от параметра проводника d, его удельной проводимости , магнитной проницаемости материала проводника и частоты переменного тока , проходящего по проводнику, показан на рис. 11.26.

При токах большой частоты (радиочастотах) ток в центре проводника отсутствует. Поэтому такие проводники делают трубчатыми, т.е. полыми.

На величину активного сопротивления проводника R оказывает влияние и эффект близости.

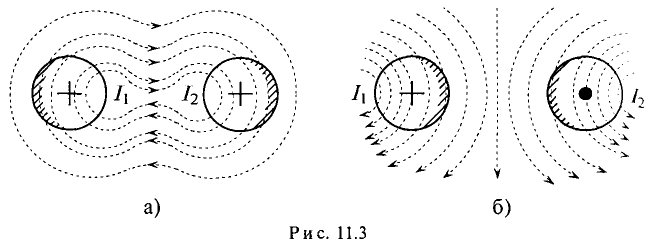
Если токи в двух параллельных проводах, расположенных близко друг к другу, направлены в одну сторону, то элементы сечения водников, удаленных на большее расстояние друг от друга, цепляются с меньшим магнитным потоком и имеют большую плотность тока (заштриховано на рис. 11.3а), чем элементы сечения проводников, расположенные близко друг к другу.

Если же токи в близко расположенных параллельных проводах направлены в различные стороны, то большая плотность тока на-дается в элементах сечения проводников, расположенных ближе друг к другу (заштриховано на рис. 11.36).

Таким образом, эффект близости в проводниках также влияет активное сопротивление проводников за счет наведения в различных элементах сечений проводников различных ЭДС взаимоиндукции, направление которых определяется правилом Ленца.

Видео:Почему Uc отстает от Ic на 90⁰ │КОНДЕНСАТОР│Сдвиг фаз между током и напряжениемСкачать

Цепь с идеальной индуктивностью

Идеальной называют индуктивность L такой катушки, активным сопротивлением R и емкостью С которой можно пренебречь, т.е. R= О и С=0.

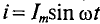
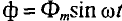
Если в цепи идеальной катушки индуктивностью L (рис. 11.4а) проходит синусоидальный ток , то этот ток создает в катушке синусоидальный магнитный поток , который индуктирует в катушке ЭДС самоиндукции, равную согласно (9.11)

так как

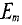
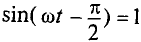
Очевидно, эта ЭДС достигает своего амплитудного значения тогда, когда :

Тогда

Таким образом, ЭДС самоиндукции в цепи с идеальной индуктивностью L, как и ток, вызвавший эту ЭДС, изменяется по синусоидальному закону, но отстает от тока по фазе на угол 90° = 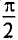(рис. 11.46, в).

По второму закону Кирхгофа для мгновенных значений можно записать

Откуда

Тогда напряжение, приложенное к цепи с идеальной индуктивностью (см. (11.5)):

Очевидно, напряжение достигает своего амплитудного значения U_m тогда, когда :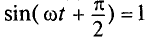

Следовательно,

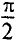
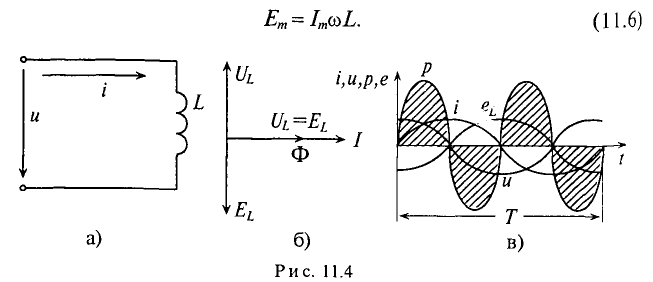
Таким образом, напряжение, приложенное к цепи с идеальной ин-ивностью, как и ток в этой цепи, изменяется по синусоидально-жону, но опережает ток по фазе на угол 90°= (рис. 11.46, в).

Резюмируя все вышесказанное, можно сделать вывод: для существования тока в цепи с идеальной индуктивностью необходимо ожить к цепи напряжение, которое в любой момент времени но по величине, но находится в противофазе с ЭДС, вызванной таким током (рис. 11.46, в).

Временная диаграмма (рис. 11.4в) еще раз иллюстрирует правило Ленца: ЭДС 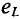противодействует изменению тока.

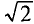
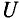
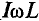
Если уравнение (11.10) разделить на =1,41, то получается =, откуда

Это уравнение (11.12а) и есть математическое выражение закона Ома для цепи синусоидального тока с идеальной индуктивностью. Очевидно, знаменатель этого уравнения есть не что иное, как сопротивление, которое называют индуктивным сопротивлением X_L.

Закон Ома для этой цепи можно записать иначе:

Индуктивное сопротивление X_L — это противодействие, которое ЭДС самоиндукции e_L оказывает изменению тока.

Реактивная мощность в цепи с индуктивностью

Мгновенная мощность для цепи синусоидального тока с идеальной катушкой равна произведению мгновенных значений напряжения и тока

где

Следовательно,

Полученное уравнение умножают и делят на 2:

Таким образом, мощность в цепи синусоидального тока с идеальной катушкой индуктивности изменяется по синусоидальному закону с двойной частотой.

Следовательно, среднее значение этой мощности за период Яс, как и любой синусоидальной величины, т. е. активная потребляемая мощность, в этой цепи равна нулю, Р= 0.

Временная диаграмма (рис. 11,4в) подтверждает этот вывод. На диаграмме видно, что мгновенная мощность (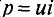) в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой.

То есть в 1-ю и 3-ю четверти периода мощность (энергия) источника накапливается в магнитном поле индуктивности. Максимальное значение накапливаемой в магнитном поле идеальной катушки энергии по (9.12) равно

Во 2-ю и 4-ю четверти периода эта мощность (энергия) из магнитного поля идеальной катушки возвращается к источнику.

Таким образом, в цепи переменного тока с идеальной катушки мощность не потребляется (Р= 0), а колеблется между источником и магнитным полем индуктивности, загружая источник и провода.

Такая колеблющаяся мощность (энергия), в отличие от активной, потребляемой, называется реактивной.

Обозначается реактивная мощность буквой Q и измеряется в варах, т.е. [Q]=вар (вольт-ампер реактивный).

Величина реактивной мощности в рассматриваемой цепи определяется выражением

Так как реактивная мощность Q_L имеет место в цепи с индуктивным сопротивлением, то индуктивное сопротивление считается реактивным сопротивлением X индуктивного характера, т. е. X_L.

Видео:RLC цепь│Задача. Определить ток, напряжения и мощности в цепиСкачать

Цепь с емкостью

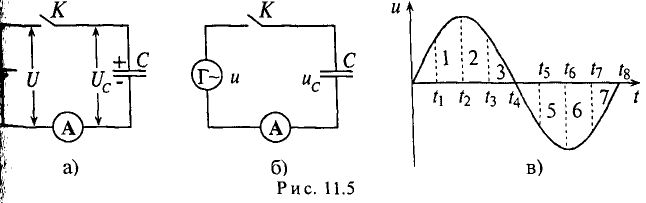
Если конденсатор емкостью С подключить к источнику с постоянным напряжением U (рис. 11.5а), то ток зарядки конденсатора ходит в цепи очень короткое время, пока напряжение на конденсаторе U_c не станет равным напряжению источника U.

Ток в рассматриваемой цепи (рис. 11.5а) практически отсутствует (амперметр А покажет I=0).

Если же конденсатор подключить к источнику с синусоидальным напряжением (рис. 11.56), то ток в цепи конденсатора существует все время, пока цепь замкнута, и амперметр А покажет этот ток. Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжена конденсаторе U_c отстает по фазе от напряжения источника и зарядке, и при разрядке конденсатора. Например, пока напряжение на конденсаторе достигает значения 1, напряжение источника достигнет значения 2 (рис. 11.5в), т. е. конденсатор заряжается; пока конденсатор зарядится до напряжения 2, напряжение источника уменьшится до напряжения 3 — конденсатор разряжается на источник и т.д. Однако ток проходит только в цепи конденсатора. Через диэлектрик конденсатора ток не проходит.

Таким образом, если к конденсатору емкостью С приложено синусоидальное напряжение 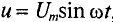, то в цепи конденсатора проходит ток i (рис. 11.6а):

где q= Си согласно (6.3).

Очевидно, ток в цепи конденсатора достигает амплитудного значения тогда, когда :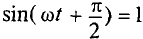

Тогда

Как видно, ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90°=

Следовательно, напряжение отстает по фазе от тока на 90° = (рис. 11.66).

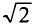
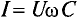
Если уравнение (11.17) разделить на = 1,41, то получится равенство или

Это равенство (11.19а) и является математическим выражением закона Ома для цепи переменного тока с емкостью.

Очевидно, знаменатель этого равенства является сопротивлением конденсатора Х_с, которое называется емкостным сопротивлением:

Когда закон Ома для цепи с конденсатором можно записать:

Емкостное сопротивление — это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему (рис. 11,5а).

Реактивная мощность в цепи с конденсатором

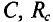
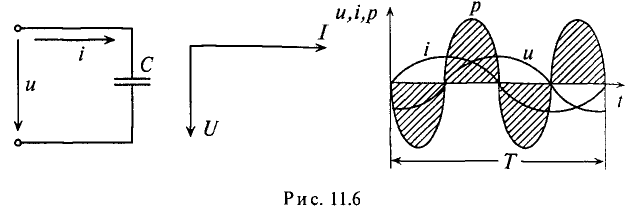
Если в цепи конденсатора емкостью = 0 (рис. 11.6а) проходит ток i, изменяющийся по синусоидальному закону:

Напряжение и, приложенное к этому конденсатору (рис. 11.6), будет равно

Мгновенная мощность в цепи с конденсатором

Мощность в цепи с конденсатором, подключенным к источнику с синусоидальным напряжением, изменяется по синусоидальному закону с двойной частотой (рис. 11.6в).

Следовательно, активная мощность Р в рассматриваемой цепи 1С. 11.6а), равная среднему значению мгновенной мощности за период, имеет нулевое значение, Р= 0.

Это следует и из временной диаграммы (рис. 11.6в). На временной диаграмме видно, что изменение мгновенной мощности р по синусоидальному закону происходит с двойной частотой: 2-ю и 4-ю четверти периода мощность (энергия) источника накапливается в электрическом поле конденсатора.

Максимальное значение энергии, накапливаемой в электрическом поле конденсатора, равно

В 1-ю и 3-ю четверти периода эта мощность (энергия) из электрического поля конденсатора возвращается к источнику.

Таким образом, в цепи переменного тока с конденсатором происходит колебание мощности (энергии) между источником и электрическим полем конденсатора. Такая колеблющаяся, но не потребляемая мощность называется реактивной мощностью.

Величина реактивной мощности в цепи конденсатора определяется выражением

Из временных диаграмм (рис. 11.4в, 11.6в) видно, что реактивная мощность в цепи конденсатора изменяется в противофазе с реактивной мощностью в цепи с идеальной катушкой. Отсюда и знак «минус» в уравнении (11.21) — аналитическом выражении мгновенной мощности в цепи с конденсатором.

Так как реактивная мощность Qc имеет место в цепи с емкостным сопротивлением, то это емкостное сопротивление считается реактивным сопротивлением Х емкостного характера (Х_с).

Видео:Что такое ИМПЕДАНС | РЕАКТИВНОЕ СОПРОТИВЛЕНИЕСкачать

Расчет линейных электрических цепей синусоидального тока

Расчет электрических цепей синусоидального тока производится преимущественно с помощью векторных диаграмм. В нашей главе рассматривается расчет неразветвленных цепей синусоидального тока, содержащих активное сопротивление R, активность L и емкость С в различных сочетаниях.

Цепь с активным сопротивлением и индуктивностью

Если по цепи с реальной катушкой, обладающей активным сопротивлением R и индуктивностью L, проходит синусоидальный ток 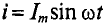(рис. 12.1а), то этот ток создает падение напряжения на активном сопротивлении проводников катушки и индуктивном сопротивлении катушки

Следовательно, по второму закону Кирхгофа, для мгновенных значений, приложенное к реальной катушке напряжение можно записать

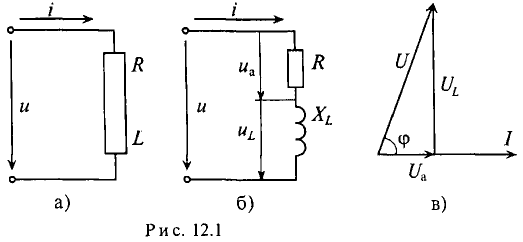
Это равенство справедливо для неразветвленной цепи синусоидального тока с последовательно включенными активным сопротивлением R и индуктивным сопротивлением X_L (рис. 12.16).

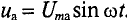
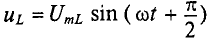
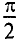
Активное напряжение (рис. 11.16) совпадет по фазе с током и может быть записано . Индуктивное напряжение опережает ток на угол 90° = .

Мгновенное значение напряжения, приложенного к цепи, определяется алгебраической суммой мгновенных значений напряжений 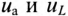согласно (12.1). А действующее значение этого напряжения U определяется геометрической суммой их действующих значений

Это равенство лежит в основе построения векторной диаграммы (рис. 12.1 в).

Из векторной диаграммы (рис. 12.1 в) видно, что напряжение U, приложенное к реальной катушке, опережает по фазе ток 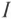на угол ф. Мгновенное значение этого напряжения может быть записано:

где ф — это международное обозначение угла сдвига фаз между током и напряжением для любой цепи переменного тока.

Воспользовавшись теоремой Пифагора для определения гипотенузы прямоугольного треугольника, по векторной диаграмме (рис. 12.1 в) определяется напряжение

Равенство (12.4) является математическим выражением закона Ома для цепи синусоидального тока с активным R и индуктивным XL сопротивлениями в неразветвленной цепи.

Знаменатель этого равенства является сопротивлением этой цепи, которое называется полным, или кажущимся, сопротивлением цепи синусоидального тока. Обозначается кажущееся (полное) сопротивление любой цепи переменного тока буквой Z:

где Z_k — полное, или кажущееся, сопротивление реальной катушки.

Тогда закон Ома для любой цепи переменного тока в общем виде можно записать

где Z — кажущееся сопротивление этой цепи.

Треугольники напряжений, сопротивлений, мощностей

Треугольник, все стороны которого изображены векторами напряжений, называется треугольником напряжений. Пользуясь векторной диаграммой для неразветвленной цепи с активным и индуктивным сопротивлениями (рис. 12.1в), выделяем треугольник напряжений (рис. 12.2а).

Связь между напряжениями в данной цепи можно рассматривать как соотношение между сторонами и углами прямоугольного треугольника:

Если все стороны треугольника напряжений разделить на ве-1ину тока в цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают сопротивления цепи, т. е. получится треугольник составлений (рис. 12.16). Сопротивления не являются векторными величинами. Из треугольника сопротивлений можно определить:

Обычно тригометрические функции угла ф определяются из треугольника сопротивлений отношением (12.9).

Если все стороны треугольника напряжений умножить на величину тока цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают мощности цепи, т.е. получится треугольник мощностей (рис. 12.2в).

Произведение напряжения и тока цепи характеризует полную мощность цепи

которая измеряется в вольт-амперах, т.е.

Однако потребляется в цепи только часть полной мощности — активная мощность

где cos ф показывает, какая часть полной мощности 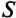потребляется в цепи, поэтому cos ф называют коэффициентом мощности:

Полная мощность цепи S называется кажущейся. Из того же треугольника мощностей (рис. 12.2в) записать:

Построив треугольники напряжений, сопротивлений и мощностей для любой цепи синусоидального тока, по выражениям (12.7)—(12.14) можно рассчитать параметры этой цепи.

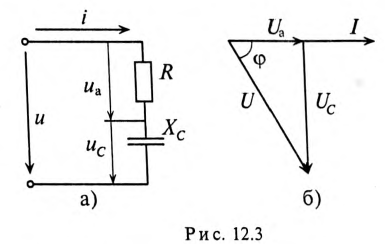
Цепь с активным сопротивлением и емкостью

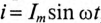
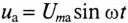
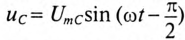
Если в цепи с последовательно включенными активным сопротивлением R и емкостью С протекает синусоидальный ток , то он создает падение напряжения на активном сопротивлении и на емкостном сопротивлении . Векторная диаграмма для этой цепи изображена на рис. 12.36.

Напряжение цепи изменяется, как и ток, по синусоидальному закону и отстает по фазе от тока на угол ф

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Почему UL опережает iL на 90°│Сдвиг фаз между UL и iL│Катушка в цепи переменного токаСкачать

Цепь с активным сопротивлением

Видео:Урок 25. Что такое Переменный ТОК | Практические примерыСкачать

Напряжение и ток

Цепь, изображенная на рис. 5 -17, обладает активным сопротивлением г и индуктивностью L. Примером такой цепи может служить катушка любого электромагнитного прибора или аппарата.

При прохождении переменного тока i в цепи будет индуктироваться э. д. с. самоиндукции e_L .

Согласно второму правилу Кирхгофа u + e_L = i r

откуда напряжение на зажимах цепи

Первая слагающая u_а = i r называется активным напряжением, мгновенное значение которого пропорционально току, а вторая u_L = — e_L = L( d i /dt) реактивным напряжение м, мгновенное значение которого пропорционально скорости изменения тока.

Если ток изменяется по закону синуса

Рис. 5-17, Цепь с активным сопротивлением и индуктивностью.

Оно изменяется также синусоидально, совпадая по фазе с током.

Амплитудное значение активного напряжения

а действующее значение

Оно изменяется синусоидально, опережая по фазе ток на 90°.

Амплитудное значение реактивного напряжения

а действующее значение

Напряжение на зажимах цепи

Напряжение на зажимах изменяется синусоидально, опережая ток по фазе на угол φ.

На рис. 5-18 показаны графики; i , и_a, u_L и и, а на рис. 5-19 — векторная диаграмма цепи. На диаграмме векторы напряжений U, U _a и U _L образуют прямоугольный треугольник напряжений, из которого непосредственно следует со отношение, связывающее эти величины:

Аналогичная зависимость имеет место и для амплитудных значений

Угол сдвига фаз между напряжением на зажимах

Рис 5-18. Графики тока и напряжения в цепи с активным сопротивлением и индуктивностью.

Рис 5 -19. Вектор ная диаграмма це пи с активным сопротивлением и индуктивностью.

цепи и током в ней находится из треугольника напряжений по одной из формул

Чем больше реактивное напряжение по сравнению с ак тивным, тем на больший угол ток отстает по фазе от напря жения на зажимах цепи.

Видео:Резистор в цепи переменного(синусоидального) токаСкачать

Сопротивления цепи

Уравнение (5-30) можно переписать в следующем виде

откуда ток в цепи

называется полным сопротивлением цепи.

Сопротивления r, x_L и z графически можно изобразить сторонами прямоугольного треугольника — треугольника сопротивлении (рис. 5-20), который можно получить из треугольника напряжений, уменьшив каждую из его сторон в I раз.

Так как треугольники сопротивлений и напряжений подобны, то угол сдвига φ между напряжением и током, равный углу между сторонами треугольника z и r, можно определить через

Рис 5-20. Треугольник сопротивлений цепи с активным сопротивлением и индуктивностью

Видео:Активное сопротивление в цепи переменного токаСкачать

Мощности

Мгновенное значение мощности р = u i = U_м sin (ωt + φ) I _м sin ωt = U_м I _м sin (ωt + φ) sin ωt Учитывая, что

sin (со/ + φ) sin ωt = 1/2 cos φ — 1/2 cos (2 ωt + φ)

а также (5-28), можно написать другое выражение ной мощности

Р = U I cos φ — U I cos (2ωt + φ)

Написанное выражение состоит из двух членов: постоянного, независимого от времени UI cos φ и переменного си-

нусоидального U I cos (2ωt + φ). Среднее значение мощности за период, которым обычно пользуются при расчете цепей переменного тока, будет равно постоянному члену UI cos φ , так как среднее значение за период синусоидальной функции равно нулю.

Таким образом, среднее значение мощности цепи равно произведению действующих значений напряжения и тока, умноженному на cos φ , т.е.

Следовательно, средняя мощность цепи равна среднему значению мощности в активном сопротивлении. Поэтому среднюю мощность любой цепи называют; еще и активной мощностью.

Реактивная мощность цепи :

т.е. реактивная мощность цепи равна произведению действующих значений напряжения и тока, умножен ному на sin φ .

Рис.5- 21. Т ре угольник мощностей

Полной мощностью цепи называется произведение действующих значений напряжения и тока, т. е.

Учитывая, что sin 2 φ + cos 2 φ = 1 можно написать: (U I cos φ ) 2 + (U I sin φ ) 2 = ( U I ) 2

Мощности Р, Q и S графически можно изобразить сторонами прямоугольного треугольника — тре у го ль ника мощностей (рис 5-21), который можно получить из треугольника напряжений, умножая на I все его стороны.

т.е отношение активной мощности к полной называется коэффициентом мощности.

Единица полной мощности с называется вольт-ампер (в •а).

Необходимость применения понятия полной мощности обусловлена тем, что конструкция, габариты, вес и стоимость машины или аппарата определяются их номинальной полной мощностью S_н = U_н I_н а полная мощность S при том или ином режиме работы их определяет степень их использования.

Статья на тему Цепь с активным сопротивлением

Похожие страницы:

Понравилась статья поделись ей

Leave a Comment

Для отправки комментария вам необходимо авторизоваться.

Видео:Мощность в цепи переменного тока. 11 класс.Скачать

Уравнения мгновенных значений тока и напряжения в цепи с активным сопротивлением

«Физика — 11 класс»

Активное сопротивление

Сила тока в цепи с резистором

Есть цепь, состоящая из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R.

Сопротивление R называется активным сопротивлением, т.к. при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора.
Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.
Напряжение на зажимах цепи меняется по гармоническому закону:

u = U_m cos ωt

Мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения.
По закону Ома мгновенное значение силы тока:

В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряжения, а амплитуда силы тока определяется равенством

Мощность в цепи с резистором

В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение меняются.
При прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет меняться во времени.

Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой

Р = I 2 R

Мгновенная мощность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой

Р = i 2 R

Cреднее значение мощности за период (используем формулу для мгновенного значения силы тока и выражение ):

График зависимости мгновенной мощности от времени (рис.а):

Согласно графику (рис.б) среднее за период значение cos 2ωt равно нулю, а значит равно нулю второе слагаемое в формуле для среднего значения мощности за период.

Тогда средняя мощность равна:

Действующие значения силы тока и напряжения.

Среднее за период значение квадрата силы тока:

Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы переменного тока.
Действующее значение силы переменного тока обозначается через I:

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

Действующее значение переменного напряжения определяется аналогично:

Закон Ома для участка цепи переменного тока с резистором в действующих значениях:

В случае электрических колебаний важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность.
Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.

Действующие значения непосредственно определяют среднее значение мощности Р переменного тока:

р = I 2 R = UI.

Итак:
Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Электромагнитные колебания. Физика, учебник для 11 класса — Класс!ная физика

🎦 Видео

Активное и реактивное сопротивление в цепи переменного тока. Практ. часть -решение задачи. 11 класс.Скачать

Активное и реактивное сопротивление цепи переменного тока. 11 класс.Скачать

АКТИВНОЕ И РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ | ОБЪЯСНЯЮ НА ПАЛЬЦАХСкачать

[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать

11 класс урок №15 Активное сопротивление в цепи переменного токаСкачать

Классификация элементов электрических цепей. Активное, емкостное и индуктивное сопротивленияСкачать