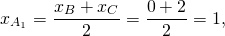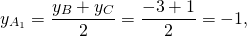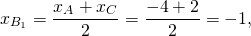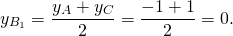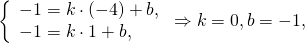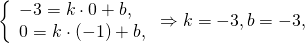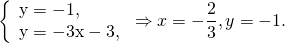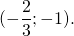Уравнения медиан треугольника и точку м точку пересечения медиан (4 видео)

Точка пересечения медиан треугольника

Как найти точку пересечения медиан треугольника, зная координаты его вершин?

Поскольку все медианы треугольника пересекаются в одной точке, достаточно составить уравнения двух медиан и найти координаты их точки пересечения.

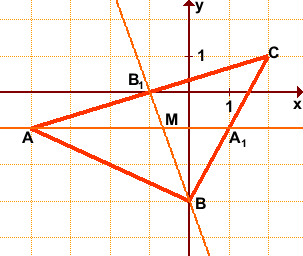
Найти координаты точки пересечения медиан треугольника с вершинами в точках A(-4;-1), B(0;-3), C(2;1).

Обозначим середины сторон BC и AC через A₁ и B₁ соответственно. По формулам координат середины отрезка

Составим уравнения медиан AA₁ и BB₁.

Уравнение медианы AA₁ можно найти как уравнение прямой, проходящей через две точки A(-4;-1) и A₁(1;-1).

то есть уравнение прямой AA₁ y= -1.

B(0;-3), B₁(-1;0). Найдём уравнение медианы BB₁.

откуда уравнение прямой BB₁ y= -3x-3.

Координаты точки пересечения прямых AA₁ и BB₁ ищем как решение системы уравнений

Поскольку все медианы медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины, можно найти координаты концов любой медианы, а затем точку, которая делит медиану в отношении 2:1, начиная отсчёт от точки, которая является вершиной треугольника.

Например, в условиях предыдущей задачи — найти координаты точки пересечения медиан треугольника с вершинами в точках A(-4;-1), B(0;-3), C(2;1), —

зная координаты A₁(1;-1), найдём координаты точки M. Точка M пересечения медиан треугольника делит отрезок AA₁ в отношении 2:1, считая от точки A.

Содержание

Урок 1. Медианы треугольника. Точка пересечения медиан
Точка пересечения медиан треугольника
Медиана
Точка пересечения медиан
Что мы узнали?
📹 Видео

Видео:Точка пересечения медиан в треугольникеСкачать

Урок 1. Медианы треугольника. Точка пересечения медиан

Медианы треугольника. Точка пересечения медиан.

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Уравнения медиан треугольника и точку м точку пересечения медиан

Теорема. Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.

Точка пересечения медиан треугольника является центром тяжести этого треугольника.

Задача 1 Точка пересечения медиан треугольника отстоит от его вершин на расстояния, равные 4, 6 и 8. Найти длины медиан треугольника.

Решение. Пусть в треугольнике АВС AM, BE и CD — медианы, К – точка их пересечения, KС=4, KА=6 и КВ=8.

Так как , то есть на отрезок КА приходится 2 части, а на отрезок КМ – одна часть, то вся медиана АМ состоит из трех равных частей и

Получаем .

Задача 2 Медианы AM и СК треугольника АВС взаимно перпендикулярны и равны соответственно 6 и 9 . Вычислить длины сторон АВ и ВС.

Решение. Пусть медианы АМ и СК треугольника АВС пересекаются в точке Р. Тогда

поэтому и

, .

Вычислим по теореме Пифагора длины отрезков AK и СМ, получаем

, .

Теперь вычислим длины сторон АВ и ВС:

АВ=2АК=10, ВС=2СМ=.

Ответ: 10;.

Тест для самоконтроля.

1. Медиана треугольника делит пополам (выбрать один из вариантов ответов)

1) угол треугольника

2) сторону треугольника

3) две стороны треугольника

2. В каком отношении точка пересечения медиан треугольника делит каждую из медиан треугольника (выбрать правильные варианты ответов).

1) 2:1 считая от основания треугольника

2) 1:2 считая от вершины треугольника

3) 2:1 считая от вершины треугольника

4) 1:2 считая от основания треугольника

5) на две равные части

3. Если в треугольнике АВС проведена медиана АM и Р – точка пересечения медиан треугольника, то какую часть медианы АМ составляет отрезок АР? (выбрать один из вариантов ответов)

4. В треугольнике АВС проведена медиана АM и Р – точка пересечения медиан треугольника. Какую часть медианы АМ составляет отрезок РМ? (выбрать один из вариантов ответов)

5. В треугольнике АВС проведена медиана АM и Р – точка пересечения медиан треугольника. Какую часть отрезка АР составляет отрезок РМ? (выбрать один из вариантов ответов)

Посмотреть правильные ответы.

Задачи для самостоятельного решения.

1. Точка пересечения медиан треугольника отстоит от его вершин на расстояния, равные 6 см, 8 см и 12 см. Найдите длины медиан треугольника.

2. Медианы ВM и СК треугольника АВС взаимно перпендикулярны и равны соответственно 15 и 36 . Найдите длины сторон АВ и АС.

3. Медианы треугольника равны 6, 9 и 12. На каком расстоянии от вершин находится точка пересечения медиан треугольника?

4. Медианы треугольника равны 9, 12 и 18. Найдите расстояния от середин сторон треугольника до центра тяжести данного треугольника.

5. Центр тяжести треугольника отстоит от середин его сторон на расстояния. Равные 5, 6 и 7. Найдите медианы данного треугольника.

6. Точка пересечения медиан треугольника удалена от середин его сторон на расстояния, равные 2, 3 и 4. На каких расстояниях от вершин треугольника находится эта точка?

Видео:Уравнения стороны треугольника и медианыСкачать

Точка пересечения медиан треугольника

Средняя оценка: 4.1

Всего получено оценок: 243.

Средняя оценка: 4.1

Всего получено оценок: 243.

Медиана – это один из уникальных отрезков треугольника. Медиана имеет ряд свойств, полезных для решения задач, а точка пересечения медиан еще больше расширяет список этих свойств. О точке пересечения медиан, ее свойствах и пойдет речь сегодня.

Видео:№366. Докажите, что если М — точка пересечения медиан треугольника ABC, а О — произвольная точкаСкачать

Медиана

Медиана – это отрезок, соединяющий вершину треугольника с серединой отрезка противоположной стороны. Три медианы треугольника пересекаются в одной точке, которая зовется точкой пересечения медиан.

Медианы, в отличие от высот, всегда лежат внутри треугольника. Это логично, ведь отрезок медианы соединяет вершину и середину стороны. А середина стороны всегда лежит внутри треугольника.

Рис. 1. Медианы в тупоугольном треугольнике.

Если соединить два любых основания медиан отрезком, то получится средняя линия треугольника. Три средние линии треугольника образуют треугольник, подобный изначальному с коэффициентом подобия 1:2

Есть еще одно любопытное свойство медиан, которое позволит не запутаться при построении золотого сечения треугольника. Медиана в треугольнике всегда располагается между высотой и биссектрисой (исключение – равнобедренный и равносторонний треугольники).

Рис. 2. Золотое сечение произвольного треугольника.

Приведем формулу вычисления длины медианы по трем сторонам. Эта формула часто используется при решении задач, и потому ее желательно запомнить.

Зачастую ученикам проще запомнить словесную формулировку, а не заучивать формулу. Чтобы найти медиану по трем сторонам, нужно взять корень из сумм удвоенных квадратов сторон минус квадрат стороны, к которой проведена медиана. Полученный корень нужно поделить пополам.

Видео:Точка пересечения медиан.Скачать

Точка пересечения медиан

Точка пересечения медиан является одной из 3 замечательных точек треугольника, которые составляют золотое сечение треугольника.

Точка пересечения медиан треугольника имеет ряд свойств, полезных при решении задач:

Медиана точкой пересечения делится на отрезки в отношении 2:1 считая от вершины.
Три медианы, проведенные в треугольнике, делят его на 6 равновеликих треугольников. Равновеликими называют треугольники с равной площадью. Сами по себе эти фигуры имеют мало общего, но численная характеристика площади у них совпадает.
Точка пересечения медиан в треугольнике называется центроидом и является центром тяжести треугольника.

Точка пересечения медиан единственная из золотого сечения треугольника, имеет реальный физический смысл. Если из картона вырезать треугольник, тонким карандашом провести в нем медианы, то точка их пересечения будет центром тяжести плоской фигуры.

Рис. 3. Центр тяжести треугольника.

Это значит, что если установить иголку в эту точку, то фигура будет держаться на ней без прокола, исключительно за счет равновесия.

Видео:Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

Что мы узнали?

Мы привели формулу вычисления медианы по 3 сторонам треугольника. Привели несколько свойств точки пересечения медиан в треугольнике. Поговорили о реальном физическом значение центроида треугольника.