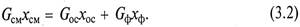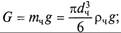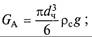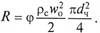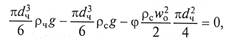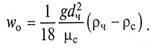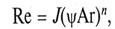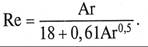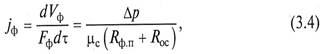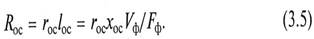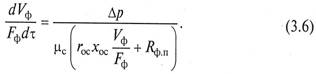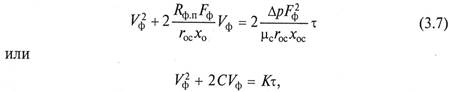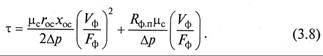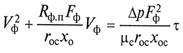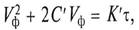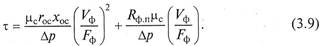Уравнения материального баланса процессов разделения (3 видео)

Содержание

Материальный баланс разделения неоднородной системы.
Материальный баланс процесса разделения
Лекция 2, разделение неоднородных систем
📽️ Видео

Видео:ОВР и Метод Электронного Баланса — Быстрая Подготовка к ЕГЭ по ХимииСкачать

Материальный баланс разделения неоднородной системы.

Неоднородными, или гетерогенными, называют системы, состоящие, по меньшей мере, из двух фаз. При этом одна из фаз является сплошной, а другая — дисперсной, распределенной в первой в раздробленном состоянии: в виде капель, пузырей, мелких твердых частиц и т. д. Сплошную фазу часто называют дисперсионной средой.В зависимости от физического состояния фаз различают следующие бинарные гетерогенные системы: суспензии, эмульсии, пены, пыли, дымы и туманы. Неоднородные системы характеризуются концентрацией дисперсной фазы и размерами образующих ее частиц. Для эмульсий и пен при определенных концентрациях дисперсной фазы возможен ее переход в сплошную; при этом фаза, бывшая сплошной, становится дисперсной. Этот переход называют инверсией фаз.В большинстве случаев дисперсные системы содержат частицы, различающиеся по размеру. Такие системы называют полидисперсными. Процессы, связанные с разделением неоднородных систем, играют большую роль в химической технологии при подготовке сырья и очистке готовых продуктов, при очистке сточных вод и отходящих газов, а также при выделении из них ценных компонентов.Применяют следующие основные методы разделения: осаждение, фильтрование и мокрую очистку газов. Осаждение — процесс разделения, при котором взвешенные в жидкости или газе твердые или жидкие частицы отделяются от сплошной фазы под действием сил тяжести (отстаивание), центробежной силы (циклонный процесс и центрифугирование), сил инерции, электростатических сил (очистка газов в электрическом поле). Фильтрование — процесс разделения с помощью пористой перегородки, способной пропускать жидкость или газ, но задерживать взвешенные частицы. Движущей силой процесса фильтрования является разность давлений. В случаях, когда разность давлений создается центробежными силами, процесс называют центробежным фильтрованием. Мокрая очистка газов — процесс разделения, основанный на улавливании взвешенных в газе частиц жидкостью. Улавливание осуществляется, как правило, под действием сил инерции. Выбор метода разделения зависит от концентрации дисперсных частиц, их размера, требований к качеству разделения, а также от разницы плотностей дисперсной и сплошной фаз и вязкости последней. Жидкие неоднородные системы можно разделить под действием сил тяжести, центробежных сил, сил давления. Рассм. основн. параметры процесса разделения жидких неоднородных систем на примере суспензий. Обознач. через тсм, то, тос массы соответственно исходной смеси, осветленной жидкости и осадка. Уравнение материального баланса системы имеет вид тсм = т0+тос. (1)Поскольку полностью разделить суспензию не удается, так как часть жидкости всегда удерживается в порах осадка капиллярными силами, материальный баланс для твердой фазы запишем в виде уравнения тсмасм = т0а0 + тосаос, (2) где асм,а0,аос — массовые доли твердого вещества соответственно в исходной смеси, осветленной жидкости и осадке.

Совместное решение уравнений (4.1) и (4.2) позволяет определить массу осадка и массу осветленной жидкости: тос = [тсм(асм- а0)]/(аос- ао);то= [тсм (аос — асм)]/(аос — а0). (3)Для исходной суспензии величины тсм и асм обычно известны. Конечная концентрация твердого вещества в осадке выбирается на основе практических рекомендаций, а также исходя из последующего использования осадка. Структура осадков, получаемых при разделении суспензий, характеризуется размерами пор, порозностью εп, удельной поверхностью f(м2/м3). Осаждение жидких неоднородных систем может происходить как под действием сил тяжести, так и под действием центробежных сил.Осаждение неоднородных систем под действием сил тяжести называется отстаиванием. Отстаивание в основном используется для предварительного разделения суспензий и эмульсий. Процесс отстаивания суспензий протекает следующим образом. Суспензия заливается в аппарат (отстойник), где под действием сил тяжести более крупные частицы начинают оседать на дно, увлекая за собой мелкие частицы. Мелкие частицы, в свою очередь, замедляют движение крупных частиц. Взаимодействие частиц при осаждении приводит к тому, что их скорости движения сближаются и становятся практически одинаковыми в каждом сечении аппарата. Однако по высоте аппарата скорости частиц различны. По мере приближения частиц к дну отстойника их движение замедляется жидкой фазой, которая вытесняется частицами и движется вверх. Через некот. время в аппарате возникают зоны с различной скоростью движения частиц. Над слоем осадка находится зона стесненного движения частиц, выше нее — зона свободного осаждения частиц, а над ней располагается осветленная жидкость. Такая схема несколько упрощает действительную картину процесса, которая обычно бывает более сложной. В аппаратах непрерывного действия зоны отстаивания по высоте не изменяются, в аппаратах периодического действия высота отдельных зон изменяется во времени до момента полного разделения суспензии на осадок и осветленную жидкость. Основной характеристикой процесса отстаивания является скорость осаждения, которая различна для легких и тяжелых частиц, для зон стесненного и свободного осаждения. Для описания в критериальной форме процесса осаждения шарообразной частицы в неподвижной неограниченной среде могут быть применены критерии подобия: Архимеда Аr, Лященко Ly и Рейнольдса Re.

Наиболее удобной формой критериальной зависимости является Ly = f(Аr).

При так называемом ламинарном режиме осаждения, когда критерии имеют значения Аr 3500, то аппараты называются сверхцентрифугами. При таких больших скоростях вращения влиянием силы тяжести на движение жидкости можно пренебречь и учитывать лишь влияние центробежной силы.Осаждение под действием центробежных сил проводится в барабанах, вращающихся со скоростью ω и имеющих радиус вращения r. Жидкая неоднородная система вводится в барабан снизу. Под действием центробежной силы и силы тяжести свободная поверхность жидкости принимает форму параболоида вращения.Различают центробежное осветление и центробежное отстаивание.Центробежное осветление проводится для очистки жидкостей, содержащих небольшое количество твердых частиц (тонкие суспензии, коллоидные растворы). При малой концентрации дисперсной фазы четкой границы между фугатом и осадком нет. По физической сущности центробежное осветление можно рассматривать как свободное осаждение частиц в поле центробежных сил.Центробежное отстаивание проводится для разделения суспензий и эмульсий. При повышении концентрации твердых частиц в суспензии образуется четкая граница раздела фаз. На первом этапе процесса происходит образование осадка, на втором — его уплотнение.Отличием процессов осаждения под действием сил тяжести от центробежных сил является то, что центробежная сила не постоянна по сечению барабана: она увеличивается с увеличением радиуса вращения. Кроме того, в отстойниках частицы проходят через постоянные поперечные сечения аппарата, а в центрифугах — через возрастающие по радиусу поперечные сечения кольцевого слоя.Рассмотрим классификацию отстойных центрифуг.В зависимости от рабочего режима (аппараты непрерывного или периодического действия), конструкции (вертикальные, горизонтальные, наклонные), способа выгрузки осадка (вручную или механически), фактора разделения (нормальные с фактором разделения Кр 3500), типа неоднородных систем (суспензия или эмульсия) различают следующие виды отстойных центрифуг:нормальные периодического действия — выгрузка осадка вручную с помощью ножей;нормальные непрерывного действия — выгрузка осадка с помощью шнека;трубчатые сверхцентрифуги периодического действия; выгрузка осадка вручную;трубчатые сверхцентрифуги непрерывного действия; разделение эмульсий;тарельчатые сепараторы непрерывного действия; разделение эмульсий.Нормальная центрифуга периодического действия представляет собой вращающийся барабан со сплошными стенками, в который вводится разделяемая суспензия.Осадок осаждается на стенках барабана и удаляется вручную. Жидкая фаза, принимая форму параболоида вращения, переливается через стенки барабана.

Билет № 28

Перемешивание жидких сред.

Перемешивание в жидких средах широко применяется в различных отраслях промышленности: в химической промышленности для приготовления суспензий, эмульсий, пен и растворов; Сп-бы перемешивания и выбор аппаратуры, для его проведения определяются целью перемешивания и агрегатным состоянием перемешиваемых материалов. Независимо от того, какая среда смешивается с жидкостью – газ, жидкость или твердое сыпучее вещество, – различают два основных способа перемешивания в жидких средах: механический (с помощью мешалок различных конструкций) и пневматический (барботаж сжатого воздуха, пара или инертного газа). Кроме того, взаимно растворимые жидкости, а также газы могут быть смешаны непосредственно в трубопроводах с помощью специальных вставок: диафрагм, сопел, труб Вентури и др., а также циркуляцией жидкостей насосами. Наиболее распространенным способом перемешивания в жидких и пастообразных средах является механическое перемешивание. Механическое перемешивание осуществляется с помощью мешалок, которым сообщается вращательное движение. В зависимости от устройства мешалки делятся на лопастные, пропеллерные, турбинные и специального назначения (якорные, рамные и листовые). Лопастные/ якорные, рамные и листовые мешалки относятся к тихоходным (частота вращения 0,15…5 с -1 ), пропеллерные и турбинные – к быстроходным (частота вращения до 40 с -1 ). Вал мешалки устанавливают в аппарате вертикально, горизонтально или наклонно.Лопастные мешалки наиболее просты по конструкции, имеют две или несколько лопастей. Устанавливают их, как правило, на вертикальном валу, ось которого совпадает с осью аппарата. Диаметр лопастей d_м =(0.15…0,5)D, где D – внутренний диаметр аппарата; ширина лопасти b = 0,25d_м. К недостаткам мешалок этого типа следует отнести низкое насосное действие мешалки (слабый осевой поток), не обеспечивающее достаточно полного перемешивания во всем объеме аппарата. Они сообщают жидкости в основном вращательное движение (тангенциальный поток). Развитие турбулентности в объеме перемешиваемой жидкости происходит медленно, циркуляция жидкости невелика. Поэтому лопастные мешалки применяют для перемешивания жидкостей, вязкость которых не превышает 50 Па·с. Эти мешалки непригодны для перемешивания в аппаратах непрерывного действия. Чтобы обеспечить перемещение жидкости в вертикальном направлении, устанавливают наклонные лопасти под углом 30…45° к оси вала. Такая мешалка способна удерживать во взвешенном состоянии частицы вещества с малым удельным весом, скорость осаждения которых невелика. Мешалки с наклонными лопастями хорошо перемешивают жидкости средней вязкости и суспензии. В аппаратах значительной высоты на одном валу устанавливают несколько пар лопастей, повернутых друг относительно друга на 90°. Расстояние между отдельными рядами выбирают в пределах (0,3…0,8)d_м в зависимости от вязкости перемешиваемой среды.Лопастные мешалки используют в качестве перемешивающего устройства в баках для приготовления и хранения связующего, парафиновой эмульсии, ящиках непрерывной проклейки древесноволокнистой массы, смесителях и другом оборудовании цехов ДВП и ДСП. При больших объемах перемешиваемой жидкости применяют лопастные мешалки (мешальные бассейны) с горизонтальным расположением оси вращения лопастей.Для перемешивания жидкостей вязкостью до 100 Па·с, а также для перемешивания в аппаратах, обогреваемых с помощью рубашки или внутренних змеевиков, в тех случаях, когда возможны выпадение осадка или загрязнения теплопередающей поверхности, применяют якорные или рамные мешалки. Их поставляют комплектно с реактором. Они имеют форму, соответствующую внутренней форме аппарата. Диаметр мешалки соответствует (0,8…0,95)D, частота вращения (0,3…1,0) с -1 .Якорные мешалки применяют для перемешивания густых вязких сред, в частности синтетических смол в реакторах. Мешалка перемешивает все компоненты смолы, очищает стенки реактора, благодаря чему улучшается теплообмен и предотвращается перегрев массы.Листовые мешалки имеют лопасти большей ширины, чем у лопастных мешалок. Они применяются для перемешивания маловязких жидкостей (вязкость менее 0,5 Па·с), интенсификации процессов теплообмена при проведении химических реакций в объеме и растворении. Для процессов растворения используют листовые мешалки с отверстиями в лопастях. При вращении такой мешалки на выходе из отверстий образуются струи, способствующие растворению твердых материалов. Листовые мешалки устанавливают на расстоянии h = (0,2…0,5)D от дна сосуда, лопастные мешалки – на расстоянии h≤0.3D. Для листовых мешалок d_м = (0,3…0,5)D , ширина лопасти b = (0,5…1,0)D,Частота вращения лопастных и листовых мешалок в зависимости от вязкости перемешиваемой среды изменяется от 0,5 до 5,0 с -1 , причем с увеличением вязкости и ширины лопастей скорость вращения мешалки уменьшается.Для предотвр. образования на поверхности жидкости воронки, ухудшающей условия перемешивания, к стенкам аппарата вдоль образующей крепят отражательные перегородки – вертикальные планки шириной 0,1D. При большой вязкости жидкости во избежание образования застойных зон за перегородками их устанавливают на расстояния от стенки, равном 0,2…1,0 ширины перегородки.Пропеллерные мешалки применяют для интенсивного перемешивания жидкостей умеренной вязкости (до 4 Па·с), для растворения, образования взвесей, быстрого перемешивания, образования маловязких эмульсий, гомогенизациии больших объемов жидкости. Эти мешалки изготавливают двух -, трех — и четырехлопастными с лопастями, изогнутыми по профилю гребного винта. Наибольшее распространение получили трёхлопастные пропеллеры. Пропеллерные мешалки создают преимущественно осевые потоки -обладают большим насосным эффектом, что особенно необходимо для предотвращения оседания твердой фазу в суспензиях. Пропеллерные мешалки следует устанавливать в цилиндрических аппаратах с выпуклыми днищами. При установке их в прямоугольных баках или аппаратах с плоскими днищами интенсивность перемешивания падает вследствие образования застойных зон (это не относится к мешалкам с горизонтальным валом).Интенсивность перемешивания пропеллерной мешалкой резко возрастает при смещении вала мешалки с осевой линии аппарата и при наклоне вала на угол 10 – 20° к вертикали. Для улучшения перемешивания больших объемов жидкости и организации направленного течения жидкости (при большом отношении высоты к диаметру аппарата) пропеллер иногда заключают в диффузор.Для пропеллерных мешалок принимают следующие соотношения основных размеров: диаметр мешалки d_м=(0,2…0,5)D; расстояние от мешалки до дна сосуда h=(0,5…1,0)d_м; высота уровня жидкости в сосуде H=(0,8 …1,2)D. Число оборотов пропеллерных мешалок достигает 40 в секунду.Недостатком пропеллерных мешалок является сложность конструкции и сравнительно высокая стоимость изготовления. В производстве древесных плит и пластиков пропеллерные мешалки используют наряду с лопастными в клееприготовительных отделениях (ящиках непрерывной проклейки) и мешальных бассейнах.Турбинные мешалки имеют форму колес водяных турбин с плоскими, наклонными или криволинейными, лопатками, укрепленными, как правило, на вертикальном валу. Турбинные мешалки обеспечивают хорошее перемешивание вязких жидкостей и суспензий (до 20 Па·с). Они используются для быстрого растворения, эмульгирования, диспергирования, для образования взвесей (размер частиц для закрытых мешалок может достигать 2,5·10 -2 м), при проведении химических реакций, абсорбции газов и интенсификации тепловых процессов. Для перемешивания в больших объемах турбинные мешалки менее пригодны, чем пропеллерные мешалки.В зависимости от области применения турбинные мешалки обычно имеют диаметр d_м=(0,15…0,65)D при H_ж/D≤2. При значительной высоте аппарата устанавливают на валу две или три мешалки. Турбинка располагается близко ко дну – на расстоянии h=(0.25…0.35)d_м.Мощность, потребляемая турбинными мешалками, работающими в аппаратах с отражательными перегородками, практически не зависит от вязкости среды.Выбор мешалки определяется условиями проведения процесса и вязкостью перемешиваемой среды. В основу их сравнительной оценки могут быть положены две наиболее важные характеристики: 1 – интенсивность перемешивающего устройства; 2 – эффективность его действия.Интенсивность перемешивания определяется временем достижения заданного технологического результата или числом оборотов мешалки при фиксированной продолжительности процесса. Действие мешалки будет тем более интенсивным, чем меньше время перемешивания (при n=const) или чем меньше число её оборотов ( при тау=const).Эффективность перемешивающего устройства определяется затратами энергии, необходимой для достижения заданного технологического результата. Например, в процессах получения суспензий эффективность перемешивания характеризуется степенью равномерн. и распределения твердой фазы в объёме аппарата; при интенсификации тепловых и диффузионных процессов – отношением коэффициентов тепло – или массоотдачи при перемешивании и без него; в процессах приготовления эмульсий – диаметром дисперсной фазы или суммарной площадью контакта фаз.Для экономичного проведения процесса перемешивания желательно, чтобы требуемый эффект перемешивания достигался за наиболее короткое время. При оценке расхода энергии перемешивающим устройством следует учитывать общий расход энергии за время, необходимое для обеспечения заданного результата перевешивания.

Видео:Разделение жидких систем. Материальный баланс процессов разделенияСкачать

Материальный баланс процесса разделения

Если в аппарат для разделения гетерогенных систем подается некоторое количество исходной смесив количестве G_см, кг, содержащей х_см (вес, %) дисперсной фазы, а после разделения образуется концентрированная дисперсная фаза в количестве G_ос с концентрацией х_ос и очищенная дисперсионная среда в количестве G_ф с концентрацией оставшейся дисперсной фазы фильтрата х_ф, материальный баланс такого процесса записывается в соответствии с уравнением (В.5) для входящих и выходящих материальных потоков

для содержащейся в них дисперсной фазы

Совместным решением уравнений (3.1) и (3.2) можно определить два необходимых для расчета технологического процесса параметра.

Разделение в поле сил тяжести (отстаивание)

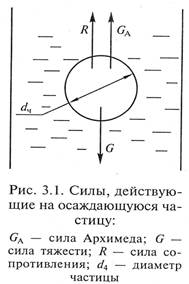
Кинетика отстаивания. При определении скорости отстаивания частицы дисперсной фазы сделаем следующие допущения: частица имеет сферическую форму; на осаждение не оказывают влияния ни другие частицы, ни стенки аппарата; плотность частицы р,, больше плотности среды ρ_с, в которой она осаждается. Скорость движения частиц постоянна.

В этом случае на частицу, движущуюся в среде со скоростью w₀, действуют следующие силы (рис. 3.1):

· сила тяжести

· подъемная сила (сила Архимеда)

Уравнения материального баланса процессов разделения

ла сопротивления

Поскольку движение частицы направлено вниз (ρ_ч > ρ_с), запишем уравнение баланса сил (уравнение осаждения частицы под действием силы тяжести)

где g – ускорение свободного падения;

φ – коэффициент гидравлического сопротивления.

Отсюда скорость осаждения может быть выражена как

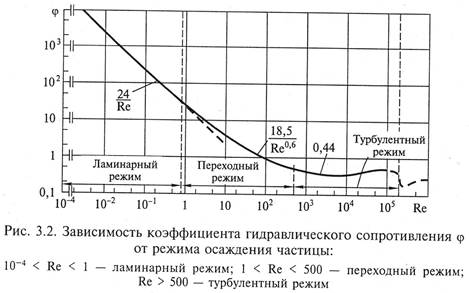
Входящий в уравнение (3.3) коэффициент гидравлического сопротивления определяется в зависимости от режима осаждения частицы (рис. 3.2).

1. При ламинарном режиме осаждения 10 -4 0,6 (формула Аллена).

3. При турбулентном режиме осаждения Re > 500, движение становится неупорядоченным, траектории частиц – извилистыми, φ ≈ 0,44 (формула Ньютона).

В турбулентной области наступает автомодельный режим, т. е. режим не зависящий от изменяемого параметра (Re).

Поскольку осаждение в промышленных аппаратах-отстойниках осуществляется при ламинарном режиме, подставив в уравнение (3.3) коэффициент гидравлического сопротивления в виде формулы Стокса, получим

Для практических расчетов скорости осаждения используют также критериальную зависимость, учитывающую фактор формы частиц ψ,

где в качестве диаметра несферической частицы используется ее эквивалентный диаметр, полученный на основании ее веса G_ч

Поскольку не всегда возможно предсказать, в каком режиме будет осаждаться частица и какую зависимость для определения скорости ее осаждения следует использовать, считается, что ламинарный режим наблюдается при Аг 4 ; турбулентный – при Аг > 8,3*10 4 .

На практике для приближенного определения скорости осаждения во всех режимах обтекания частиц можно воспользоваться зависимостью

Отстаивание является одним из самых дешевых процессов и осуществляется в аппаратах, называемых отстойниками.

Различают отстойники для разделения пылей, суспензий и эмульсий. Эти аппараты могут быть периодического, полунепрерывного и непрерывного действия.

По функциональному назначению отстойники для разделения суспензий делят на сгустители, осветлители и классификаторы.

Основной характеристикой отстойного оборудования является его производительность V_от, определяемая как

где F – площадь поверхности осаждения.

Для отстойников с несколькими поверхностями осаждения (многополочные отстойники), каждая из которых имеет площадь f_поз,

где n – число поверхностей осаждения.

Для увеличения скорости осаждения мелкодисперсных частиц используют специальные растворы – коагулянты, способствующие объединению частиц между собой, что увеличивает массу осаждаемого агломерата.

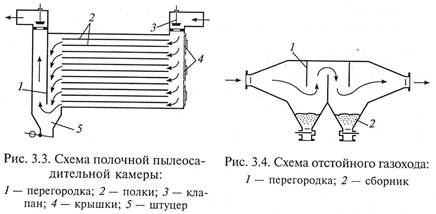
Для разделения пылей применяются полочные пылеосадительные камеры (рис. 3.3), включающие расположенные друг над другом горизонтальные полки 2, равномерное распределение газа, вдоль которых осуществляется с помощью вертикальной перегородки 1. Скорость вдоль полок регулируется клапаном 3. Разгрузка осуществляется периодически через штуцер 5 скребками, вводимыми через люки с крышками 4.

Для автоматизации разгрузки полки могут устанавливаться с наклоном, а на слой осадка может оказываться вибрационное воздействие и т. п. Аппараты аналогичных конструкций могут применяться для разделения суспензий (полочные отстойники).

Одновременное воздействие сил тяжести и инерции на разделяемую пыль осуществляется

в отстойном газоходе (рис. 3.4), сна6женном вертикальными перегородками 1, о которые ударяются, не успевающие обогнуть их содержащиеся в газе твердые частицы. За счет этого они теряют скорость и под действием силы тяжести опускаются вдоль поверхности перегородок в сборники 2, откуда отводятся периодически или непрерывно.

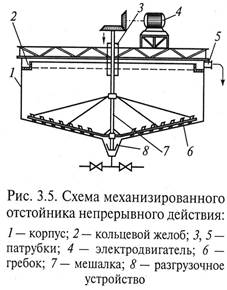
На рис. 3.5 представлен отстойник для разделения суспензий непрерывного действия с гребковой мешалкой. Отстойник состоит из цилиндрического корпуса 1 с коническим днищем, кольцевым желобом 2 и патрубком 5 для отвода очищенной жидкости, мешалки 7 с гребками 6 для перемещения постоянно образующегося осадка к разгрузочному устройству 8. Подача суспензии осуществляется через центральный патру6ок 3. Вращение мешалки с низкими скоростями, не разрушающими осадок, осуществляется с помощью электродвигателя 4.

Разделение суспензий в поле сил давления (фильтрование)

Фильтрование – процесс разделения суспензий и пылей с помощью пористых перегородок, задерживающих дисперсную – твердую фазу и пропускающих дисперсионную среду (жидкость или газ). При этом фильтрование может осуществляться как с образованием осадка, так и с за6ивкой пор (отложение осадка внутри перегородки). В дальнейшем будем рассматривать чаще встречаемое в практике фильтрование с образованием осадка.

В этом случае скорость процесса фильтрования прямо пропорциональна разности давлений, создаваемых по обеим сторонам фильтровальной перегородки (движущая сила), и обратно пропорциональна сопротивлению, испытываемому средой при ее движении через поры перегородки и слой образовавшегося осадка:

где V_ф – объем фильтрата; Fф — площадь фильтрования; τ — время проведения процесса; R_ф.п, R_ос — сопротивление фильтровальной перегородки и слоя осадка; µ_с — динамическая вязкость среды (фильтрата).

Сопротивление осадка является величиной переменной, так как фильтрование происходит с непрерывным увеличением толщины слоя осадка и, следовательно, ростом его сопротивления:

Здесь r_ос – удельное сопротивление осадка; l_ос – толщина осадка; х_ос – отношение объема осадка к объему фильтрата.

В зависимости от изменения удельного сопротивления осадка при увеличении давления различают несжимаемые (r_ос = const) и сжимаемые (r_о_c ≠ const) осадки.

Движущая сила в процессе фильтрования суспензий может создаваться: гидравлическим давлением столба жидкости над перегородкой; использованием насосов для подачи суспензии в фильтр; энергией сжатого газа над суспензией или созданием вакуума под фильтрующей перегородкой.

При этом процессы фильтрования могут осуществляться при постоянной разности давлений (Δр = const), при постоянной скорости (j_ф = const) и при переменных значениях Δр и j_Ф.

Для несжимаемых осадков с учетом зависимости (3.5) уравнение (3.4) может быть записано в виде

Для случая Δр = const результат интегрирования уравнения (3.6) в пределах 0 – V_Ф и 0 – τ после разделения переменных запишется в виде

где С и К – постоянные фильтрования, определяемые для конкретных систем экспериментальна.

Из уравнения (3.7) время на получение объема фильтрата V_Ф через поверхность фильтрования F_ф при перепаде давлений Δр составит

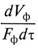
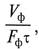
В случае j_ф = const в уравнении (3.6) можно заменить на тождественное значение и, преобразовав к виду, аналогичному (3.7), получим

где С’ и К’ – постоянные фильтрования, определяемые экспериментально.

Аналогично (3.8) получим

Сравнительный анализ уравнений (3.8) и (3.9) показывает, что процессы фильтрования с постоянным перепадом давлений при одинаковых V_Ф и F_Ф осуществляются быстрее, чем при j_Ф = const.

Аппараты для осуществления процессов фильтрования называются фильтрами.

По способу организации процесса фильтры подразделяются на периодически действующие и непрерывнодействующие.

Конструкции фильтров отличаются многообразием. Выбор их зависит от свойств разделяемых систем, производительности, условий проведения процесса (давления, температуры и т.д.).

К наиболее распространенным конструкциям для разделения пылей относится рукавный фильтр (рис. 3.б), содержащий фильтрующие элементы 1 в виде матерчатых рукавов, подвешенных к раме 2. Запыленный газ подается через патрубок 7 внутрь рукавов, в которых накапливается пыль. Расход удаляемого газа регулируется заслонкой 3. Регенерация рукавов осуществляется встряхивающим механизмом 5, а также обратным током чистого газа, подаваемого через заслонку 4 при закрытой заслонке 3. Отделенная пыль ссыпается в конический бункер и выгружается через патрубок 6.

Рукавные фильтры обеспечивают высокую степень разделения, однако име‑

ют значительное гидравлическое сопротивление, а фильтрующая ткань чувствительна к высокой температуре и наличию паров химически агрессивных веществ.

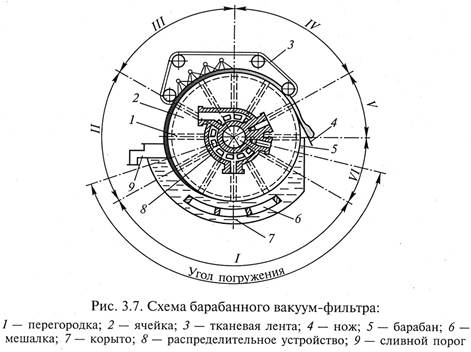
К непрерывнодействующим фильтрам с постоянным перепадом давлений для разделения суспензий относится барабанный вакуум-фильтр (рис. 3.7), состоящий из вращающегося полого барабана 5 с перфорированной боковой поверхностью, разделенной внутренними перегородками 1 на отдельные ячейки 2 и покрытого снаружи фильтровальной тканью. Его вал имеет полую цапфу, торец которой пришлифован к распределительному устройству (головке) 8. Поверхность барабана частично погружена в суспензию, находящуюся в корыте 7, уровень которой поддерживается постоянным с помощью сливного порога 9. Образуемый на поверхности барабана слой осадка снимается ножом 4. При помощи трубок каждая ячейка барабана сообщается с распределительным устройством, служащим для последовательного соединения их с источником вакуума и сжатого воздуха. Под барабаном расположена медленно качающаяся маятниковая мешалка 6, предотвращающая осаждение суспензии на дно корыта.

В зоне фильтрования I, когда поверхность фильтра погружена в корыто, каждая ячейка последовательно соединяется со сборником фильтрата, находящимся под разрежением. Затем в зоне первого обезвоживания II осадок выходит из суспензии, и филь‑

трат, отжимаемый из осадка вследствие вакуума в ячейках, собирается в том же сборнике фильтрата. После этого осадок попадает в зону промывки III, где на него из разбрызгивающих устройств подается промывная жидкость, которая с остатками фильтрата собирается в сборнике, находящемся под разрежением. В зоне второго обезвоживания IV из осадка отжимается остаток промывной жидкости. В некоторых случаях для предотвращения растрескивания, лучшей промывки и отжима на осадок накладывается непрерывная тканевая лента 3. В зоне удаления осадка V ячейка сообщается с ресивером сжатого воздуха, а в зоне регенерации 1/1 ткань продувается сжатым воздухом или промывается обратным током жидкости.

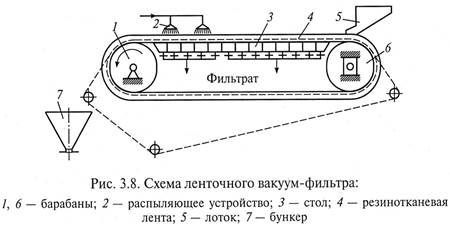
Ленточные вакуум-фильтры (рис. 3.8) непрерывного действия и постоянного перепада давлений предназначены для фильтрования агрессивных и неагрессивных быстро осаждающихся суспензий с различными размерами частиц твердой фазы.

Традиционный ленточный вакуум-фильтр состоит из бесконечной резинотканевой ленты 4, натянутой на два вращающихся барабана 1 и 6. В верхней части между барабанами лента скользит по горизонтальным направляющим (столу) 3 с прорезями, соединяющими область фильтровальной перегородки с вакуум-камерами.

Суспензия поступает на фильтр из лотка 5. Осадок либо удаляется c ленты ножом, либо сползает в бункер 7 при огибании лентой приводного барабана 1. Жидкость для промывания подается из специальных устройств 2, которые могут быть закреплены в любом месте по длине фильтра. Регенерация ткани осуществляется при ее движении в нижнем положении.

К преимуществам ленточных фильтров относятся возможности реализации оптимальных технологических режимов фильтрования и промывки осадка, регулирования толщины слоя осадка и скорости движения фильтровальной ленты, а также простота обслуживания.

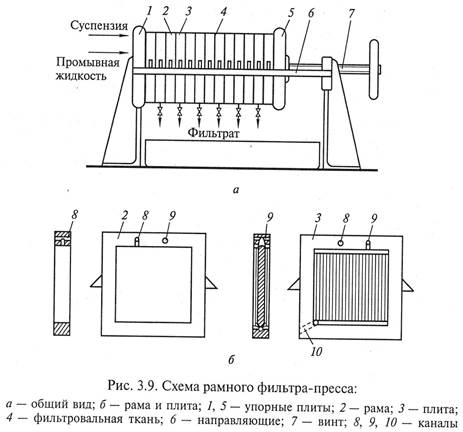
Вертикальный рамный фильтр-пресс (рис. 3.9) периодического действия применяют для разделения труднофильтрующихся суспензий. Работают они, как правило, при постоянной скорости, дешевы, компактны, обладают большой поверхностью фильтрования, приходящейся на единицу объема, хорошо приспособлены к изменяющимся свойствам суспензии.

Рамный фильтр-пресс (рис. 3.9, а) состоит из заключенного между упорными плитами 1 и 5 набора вертикально расположенных чередующихся рам 2 и плит 3 (рис. 3.9, б), опирающихся боковыми ручками на горизонтальные направляющие 6. Между ними расположена фильтровальная ткань 4.

Герметизация фильтра-пресса осуществляется зажимным винтом 7. При сборе, отверстия, выполненные в рамах и плитах, образуют каналы: 8 – для подачи суспензии, соединенные с рамами 2, и 9 – для подвода жидкости для промывки, соединенные с плитами 3. Кроме того, в плитах выполнены каналы 10 для отвода фильтрата и жидкости для промывки.

Цикл работы фильтра-пресса состоит из следующих операций: сборка; заполнение камер осадком (фильтрование); промывка осадка; отжим осадка (отдувка); разборка и разгрузка фильтра.

Механизированный камерный фильтр-пресс (рис. 3.10) периодического действия предназначен для фильтрования труднофилътруемых суспензий с высокоэффективной промывкой. Он состоит из набора горизонтальных плит 6, верхняя 1 из которых закреплена неподвижно, а остальные, включая нажимную 2, могут перемещаться вверх и вниз по специальным направляющим с помощью механизма зажима 3. Фильтровальная ткань 7 непрерывной лентой проходит между плитами 6, огибая ролики 8.

Цикл работы камерного фильтра-пресса аналогичен рамному фильтру-прессу, однако сборка, разборка и разгрузка осадка выполняются специальными механическими устройствами. В процессе движения загрязненная ткань очищается специальными ножами или щетками и промывается в специальных устройствах камеры регенерации 4. Осадок при движении ткани перегибается вместе с нею через ролики и под действием собственного веса или ножей, прижатых к ткани пружинами, удаляется с ткани и падает либо в бункер 5, либо на транспортер (на схеме не показан).

Видео:Процессы и аппараты. Материальный балансСкачать

Лекция 2, разделение неоднородных систем

РАЗДЕЛЕНИЕ НЕОДНОРОДНЫХ СИСТЕМ

2.1. КЛАССИФИКАЦИЯ НЕОДНОРОДНЫХ СИСТЕМ

Неоднородными, или гетерогенными, называют системы, состоящие, как минимум, из двух фаз: дисперсной (внутренней), обычно находящейся в тонкораздробленном состоянии, и дисперсионной (внешней), окружающей частицы дисперсной фазы.

Суспензии состоят из жидкой дисперсионной и твердой дисперсной фаз. В зависимости от размера взвешенных твердых частиц суспензии делятся на грубые с частицами размером >100 мкм; тонкие, когда размеры твердых частиц составляют 0,1. ..100 мкм, и коллоидные растворы, содержащие твердые частицы размерами ≤0,1 мкм.

Эмульсии состоят из двух жидких фаз, не растворяющихся одна в другой: дисперсионной и дисперсной. Размер частиц дисперсной фазы может колебаться в значительных пределах. Под действием гравитационной силы эмульсии обычно расслаиваются, однако тонкие эмульсии с размером капель дисперсной фазы менее 0,4. 0,5 мкм, а также содержащие стабилизаторы, становятся устойчивыми и не расслаиваются в течение продолжительного времени.

С увеличением концентрации дисперсной фазы может возникнуть состояние, когда дисперсная фаза обращается в дисперсионную и наоборот. Такой взаимный переход называется инверсией фаз.

Пены состоят из жидкой дисперсионной и газовой дисперсной фаз. По своим свойствам пены близки к эмульсиям.

Пыли и дымы состоят из газовой дисперсионной и твердой дисперсной фаз. Образуются пыли обычно при дроблении, смешивании и транспортировке твердых материалов. Размеры твердых частиц пылей составляют от 3 до 70 мкм. Дымы образуются при горении. Размер твердых частиц в дымах составляет 0,3. 5 мкм.

Туманы состоят из газовой дисперсионной и жидкой дисперсной фаз. Туманы образуются при конденсации. Размер жидких капель в тумане 0,3. 3 мкм. Пыли, туманы и дымы представляют собой аэрозоли.

2.2. МЕТОДЫ РАЗДЕЛЕНИЯ

В пищевых производствах часто возникает задача разделения неоднородных систем на составные части. Так, в производстве вина требуется его осветление, т. е. отделение взвешенных твердых частиц от жидкой фазы; пивное сусло отделяют от дробины; в производстве сахара суспензию после сатурационных аппаратов разделяют с целью получения сока, а разделяя утфель, получают кристаллический сахар. В производствах, где для получения продукта (сухого молока, молочно-овощных концентратов) используются распылительные сушилки, отходящие газы улавливаются и очищаются во избежание уноса ценных продуктов и загрязнения окружающей среды.

Основные методы разделения неоднородных систем в пищевой промышленности — осаждение, фильтрование и центрифугирование.

Осаждение — процесс разделения жидких и газовых неоднородных систем под действием гравитационных сил, сил инерции (центробежной силы) или сил электрического поля. Соответственно различают гравитационное отстаивание, циклонное и отстойное центрифугирование, электроочистку.

Фильтрование — процесс разделения жидких и газовых неоднородных систем с использованием пористой перегородки, способной пропускать жидкость и газ, но задерживающей взвешенные частицы. Фильтрование осуществляется под действием сил давления или центробежных сил. Соответственно различают просто фильтрование и центробежное фильтрование.

Фильтрование более эффективно для разделения суспензий, эмульсий и пылей, чем осаждение.

Мокрое разделение — процесс улавливания взвешенных в газе частиц жидкостью.

Применяется для очистки газов и разделения суспензий.

2.3. МАТЕРИАЛЬНЫЙ БАЛАНС ПРОЦЕССОВ РАЗДЕЛЕНИЯ

Разделению подлежит неоднородная система, состоящая из вещества а (дисперсионная фаза) и взвешенных частиц b (дисперсная фаза). Gc — количество исходной смеси, кг; хс — содержание вещества b в исходной смеси, мас. %; Gn — количество продукта, кг; хп — содержание вещества b в очищенном продукте, мас. %; Go — количество осадка, кг; xо — содержание вещества b в осадке, мас. %; о и — плотности веществ a и b.

При отсутствии потерь веществ материальный баланс разделения можно представить так:

по общему количеству веществ Gc = Gп + Gо ;

по количеству взвешенных веществ (дисперсной фазе)

Совместное решение этих уравнений позволяет определить количество очищенного продукта

(2.1)

и количество осадка

(2.2)

Содержание взвешенных частиц в очищенном продукте и в осадке выбирается в зависимости от технологических требований и зависит от метода разделения.

Эффективность разделения характеризуется эффектом разделения

Уравнениями (2.1) и (2.2) описывается также процесс смешения. Из уравнения (2.1) может быть найдена концентрация взвешенного вещества в полученной смеси

где: Gп и Gо – количества смешанных продуктов; хп и хо – массовые концентрации в этих продуктах взвешенных частиц; Gс – количество конечной смеси.

2.4. КИНЕТИКА РАЗДЕЛЕНИЯ НЕОДНОРОДНЫХ СИСТЕМ

Кинетика осаждения. Рассмотрим движение частицы под действием гравитационной силы в вязкой среде (рис. 2.1). На частицу будут действовать сила тяжести G, архимедова сила А и сила трения Т.

Рис. 2.1. Силы, действующие на частицу в вязкой среде

Объем частицы произвольной формы пропорционален линейному размеру в третьей степени: V=k 1l 3, где — коэффициент, зависящий от формы частицы; l — характеристический размер частицы (диаметр).

Если плотность твердой частицы т, а жидкости (газа, пара) ж, то на частицу действуют сила тяжести G=k1l3Tg и подъемная сила А=k1l 3 жg, направленная в сторону, противоположную направлению силы тяжести. Под действием разности этих сил частица перемещается в жидкости.

На единицу поверхности частицы со стороны жидкости действуют силы трения T= dv/dn, где — коэффициент динамической вязкости жидкости; dv/dn — изменение скорости движения жидкости в направлении, нормальном к поверхности частицы. Сумма сил трения Т зависит от площади поверхности частицы k2l2 (где kг — коэффициент, учитывающий форму частицы) и составляет T=k2l2 dv/dn

Согласно второму закону механики равнодействующая сил тяжести, подъемной и трения равна массе частицы, умноженной на ускорение:

(2.3)

Это равенство является дифференциальным уравнением осаждения частиц под действием силы тяжести.

Уравнение (2.3) не может быть решено в общем виде, поэтому для определения скорости осаждения частиц необходимо его преобразовать в критериальное уравнение.

Приведем уравнение (2.3) к безразмерному виду, поделив все его члены на

(2.4)

где: — константа, зависящая от формы частицы и называемая коэффициентом формы частицы.

После умножения членов уравнения (2.4) на параметрический критерий (отношение плотности твердой частицы к плотности жидкости ) уравнение примет вид

(2.5)

Из уравнения (2.5) можно получить критерии подобия для процесса осаждения частицы.

Из первого члена уравнения (2.5) с помощью методов теории подобия получим

(2.6)

из второго члена –

(2.7)

где: Re=— критерий Рейнольдса, характеризующий гидродинамическое подобие при обтекании частицы жидкостью.

После умножения выражения (2.6) на Re2 получим

(2.8)

где: Ar – критерий Архимеда, который характеризует отношение разности сил тяжести и подъемной к подъемной силе; v – кинематическая вязкость.

Таким образом, из дифференциального уравнения (2.3) получаем критериальное уравнение, описывающее процесс осаждения:

(2.9)

где: А – коэффициент; h – показатель степени, определяемый эксперементальным путем.

На основании экспериментальных данных установлены следующие режимы осаждения частицы в жидкости: ламинарный (Re переходный (0;2 и турбулентный (Re Для каждого режима экспериментального найдена зависимость вида (2.9):

для ламинарного режима

при Re 500 или (2.12)

По значению критерия Рейнольдса определяется скорость осаждения частицы в жидкости под действием силы тяжести

(2.13)

которая в случае ламинарного движения может быть определена по уравнению Стокса, получаемому после преобразования уравнения (2.10):

(2.14)

где: d – диаметр частицы.

Формула (2.14) справедлива для твердых частиц правильной сферической формы. Скорость осаждения частиц неправильной формы меньше.

В случае осаждения капель жидкости в жидкой среде процесс осложняется тем, что форма капель непрерывно меняется. Для определения скорости осаждения капель можно рекомендовать формулу

v0 =,

где: d — усредненный диаметр капли; — поверхностное натяжение на границах образующих фаз; — плотность среды; ж — плотность жидкости, образующей капли; c — вязкость среды.

Полученные кинетические закономерности процесса осаждения свидетельствуют о том, что скорость осаждения увеличивается с увеличением размеров и плотности частиц и уменьшается с увеличением плотности и вязкости среды, в которой происходит осаждение.

Максимальный размер твердых частиц, осаждения которых происходит по закону Стокса, можно определить, подставить в уравнение (2.14) выражение скорости из (2.13) при Re,тогда

(2.15)

Приведенные расчеты относятся к свободному отстаиванию, при котором оседающие частицы практически не оказывают взаимного влияния на движение. На практике приходится иметь дело с так называемым стесненным отстаиванием при значительных концентрациях твердых частиц в среде. При стесненном отстаивании скорость оседания частиц ниже, чем при свободном, вследствие трения и соударений частиц между собой. Для определения скорости при стесненном отстаивании в уравнения вводят поправочные коэффициенты, учитывающие концентрацию частиц в среде.

Кинетика фильтрования. При фильтровании поток жидкости проходит через пористую перегородку из твердого или волокнистого материала, которая может быть представлена как слой зернистого материала (рис. 2.2). Поры между частицами образуют каналы неправильной формы, по которым движется поток V фильтруемой жидкости.

Для описания кинетики фильтрования воспользуемся дифференциальным уравнением Навье—Стокса для установившегося одномерного движения потока

Так как это уравнение не может быть решено в общем виде, получим из него критериальное уравнение, применив методы теории подобия.

Разделив все члены уравнения на , получим

Слагаемые левой части уравнения безразмерны. Получим из них критерии подобия.

Из первого члена, заменив х на l, получают критерий Эйлера, характеризующий отношение сил давления к инерционным силам:

(2.16)

Из второго члена получает величину, обратную критерию Рейнольдса:

(2.17)

Из третьего члена, вычеркнув символы дифференцирования и направления, получают критерии Фруда, характеризующий отношение сил тяжести к инерционным силам:

(2.18)

Рис. 2.2. Схема движения жидкости через фильтрующую перегородку

Так как при фильтровании силы тяжести малы по сравнению с силами давления и трения, ими можно пренебречь. Поэтому в критериальное уравнение не вводится критерий Фруда. Для характеристики геометрических особенностей рассматриваемой системы в критериальное уравнение вводится параметрический критерий l/dэк.

Критериальное уравнение, описывающее движение потока фильтруемой жидкости через пористый слой, записывают в следующем виде:

(2.19)

где: l – толщина осадка или фильтрующей перегородки: dэк — эквивалентный диаметр каналов.

Коэффициент А и показатели степеней пит определяются экспериментально.

При малом диаметре каналов фильтрующей перегородки или каналов в осадке на фильтрующей перегородке ламинарный режим фильтрования имеет место при Re≤35.

Для ламинарного режима фильтрования зависимость (2.19) имеет вид

(2.20)

Для турбулентной области при

(2.21)

В уравнениях (2.20) и (2.21) определяющим размером является эквивалентный диаметр каналов в слое зернистого материала, а скорость потока v отнесена к свободному сечению каналов.

Эквивалентный диаметр каналов в слое зернистого материала где — доля пустот в слое зернистого материала, или коэффициент свободного объема; — удельная площадь поверхности зерен, т. е. площадь поверхности зерен, находящихся в единице объема слоя (в м2/м3):

(2.22)

где: V – общий объем, занимаемый зернистым слоем; Vo – объем, занимаемый

частицами, образующими слой, т. е. V-Vo=Vсв – свободный объем (объем каналов в слое); Fз – поверхность зерна; Vз – объем зерна.

Эквивалентный диаметр каналов в слое может быть выражен через диаметр частиц (зерен) dз.

Эквивалентный диаметр каналов в слое может быть выражен через диаметр частиц (зерен) d3.

Для частиц неправильной формы

(2.23)

где: Ф – фактор формы частиц; Ф=Fш/F; Fш – площадь поверхности шара, имеющего тот же объем, что и рассматриваемая частица площадью поверхности F. Например, для куба Ф = 0,806, для цилиндра Ф = 0,69, для диска Ф = 0,32. Значение фактора формы частиц приводятся в справочниках.

Фактор формы частиц связан с коэффициентом формы частиц соотношением.

Движение потока жидкости при фильтровании обычно ламинарное. Это обстоятельство позволяет пользоваться уравнением (2.20).

Перепишем уравнение (2.20) в явной форме

(2.24)

и введем в него вместо эквивалентного диаметра dэк значение его из уравнения (2.23), а вместо скорости в каналах v – скорость vf, отнесенную к общей площади фильтра и определяемую соотношением Произведя в уравнении (2.24) указанные замены, получим

(2.25)

т. е. скорость фильтрования через слой пористого материала прямо пропорционально квадрату диаметра частиц зернистого материала, образующего фильтровальный слой, и обратно пропорциональна вязкости фильтруемой жидкости.

С другой стороны, скорость фильтрования

(2.26)

Сопоставив равенство (2.26) с уравнением (2.25), найдём

откуда

Удельное сопротивление фильтрующего слоя

т. е. удельное сопротивление фильтрующего слоя прямо пропорционально вязкости жидкости и обратно пропорционально квадрату диаметра частиц, образующих слой.

Основное кинетическое уравнение фильтрования можно записать в следующем виде:

1. Назовите признаки, которые лежат в основе классификации неоднородных систем. Какие вы знаете неоднородные системы? 2. Перечислите методы разделения неоднородных систем. 3. Какие величины определяются из материального баланса процессов разделения? Что характеризует эффект разделения? 4. Какие критерии гидродинамического подобия характеризуют процесс осаждения? 5. Какими методами получено критериальное уравнение осаждения? 6. При каких режимах может происходить процесс осаждения? 7. Как зависит скорость осаждения от вязкости дисперсионной фазы и плотности дисперсной? 8. Какое уравнение описывает процесс осаждения при ламинарном режиме? 9. Какие силы и критерии подобия характеризуют процесс фильтрования? 10. Перечислите параметры, определяющие значение скорости фильтрования.