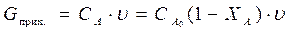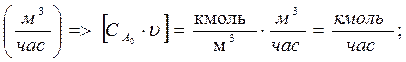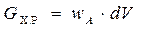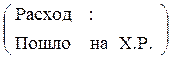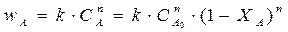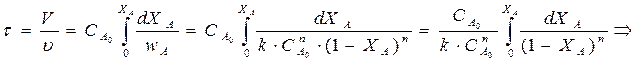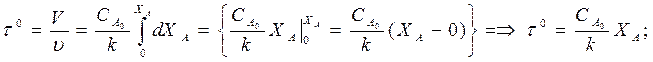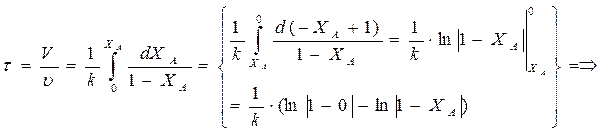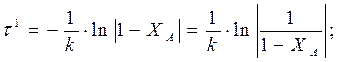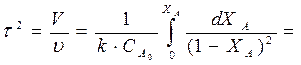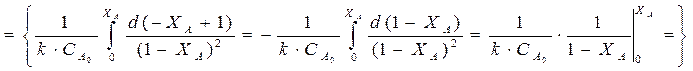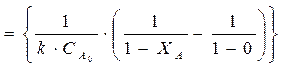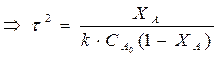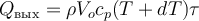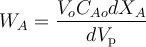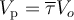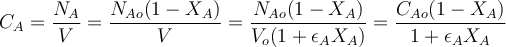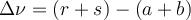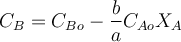Уравнения материального баланса для рив (6 видео)

П. Реактор идеального вытеснения (РИВ)

В РИС все параметры по объему постоянны.

Физическая модель РИВ-Н– длинная узкая труба, в которой все частицы движутся в заданном направлении, не перемешиваясь и вытесняя, подобно поршню, находящиеся впереди частицы потока и постепенно потоки вещества претерпевают превращение по высоте реактора. Время пребывания всех частиц в гаком реакторе постоянно: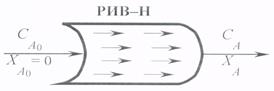

Все характеристики (концентрация С_A, степень превращения Х_А, температура Т и др.) изменяются плавно по объему реактора,поэтому материальный баланс для всего объема реактора составить нельзя.

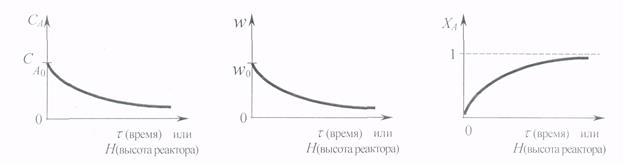
Рис.2. Графики зависимостей:

а) С_А=f (τ или H) б) w= f (τ или H) в)Х_А= f (τ или H)

— скорость процесса к единице объема

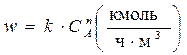
Выбирают бесконечно малый объем реактора dVи для него составляют материальный баланс. Затем проводят интегрирование этих бесконечно малых объемов по всему объему реактора.

Пусть простая необратимая реакция протекает в реакторе без изменения объема υ:

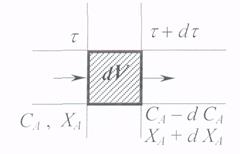реагент продукт А → R . C_Aпонижается, Х_А увеличивается. Материальный баланс процесса: G_прих.=G_расх., G_расх.=G_{улетевш.частиц} +G_{частиц.прореагр., в ХР}

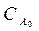
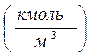
где ,С _А — соответственно начальная и текущая концентрации ;

υ- объемный расход

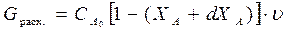
где V- объем реактора (м 3 );

dV- элементарный объем реактора (м 3 ).

;

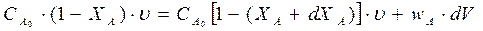
(Приход)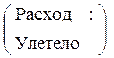

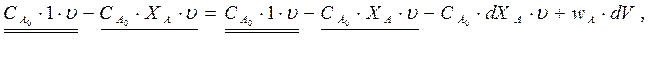
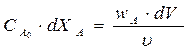
— Уравнение мат. баланса

элементарного объема РИВ-Н

Для получения уравнения мат. баланса всего реактора полученное уравнение после разделения переменных проинтегрируем (по объему всего реактора):

—Характеристическое уравнение РИВ-Н.

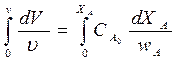
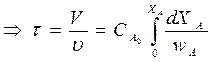
где w_A находим, зная кинетику процесса.

Характеристическое уравнение РИВ-Н позволяет, зная кинетику процесса

(для нахождения w_А), определить время τпребывания реагентов в реакторе доля достижения заданной степени превращения Х_А, а затем — и размеры реактора.

Для реакции п -го порядка :

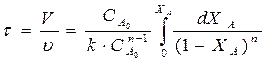
где п — порядок реакции.

— зависит только от степени превращения Х_А и не зависит от начальной концентрации ;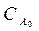

В некоторых производственных реакторах степень превращения Х_А столь незначительна, что для расчета можно применить модель РИВ— это трубчатые контактные аппараты с катализатором в трубах или межтрубном пространстве («кожухотрубчатые»), служащие для гетерогенных газофазных реакций.

Модель вытеснения также применяется при проектировании жидкофазных трубчатых реакторов с большим отношением длины трубы к ее диаметру.

При одинаковых условиях проведения одной и той же реакции для достижения равной глубины превращения среднее время пребывания реагентов в проточном реакторе идеального смешения больше, чем в реакторе идеального вытеснения. В РИС концентрации во всех точках равны конечной концентрации, а в РИВ в 2-х соседних точках концентрации реагентов отличаются. Скорость реакции, согласно ЗДМ пропорциональна концентрации реагентов. Следовательно в РИВ она всегда выше, чем в РИС. Т.е. требуется меньшее время пребывания для достижения той же глубины превращения.

Дата добавления: 2016-06-02 ; просмотров: 4296 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Содержание

Расчёт изотермического РИВ
Уравнение материального баланса рив в реакторе вывод. Реактор идеального вытеснения (РИВ). Способы его осуществления
Характеристические уравнения идеальных типов изотермических реакторов
из «Реакторы в химической промышленности»
Лекция № 12 Гидродинамические модели реакторов. Вывод характеристических уравнений.
🔥 Видео

Видео:Процессы и аппараты. Материальный балансСкачать

Расчёт изотермического РИВ

Описание модели РИВ

Реактор идеального вытеснения представляет собой длинный канал, через который реакционная смесь движется в поршневом режиме, при котором каждый ограниченный двумя плоскостями перпендикулярными оси потока элемент не смешивается ни с предыдущими ни с последующими элементами.

Схема реактора идеального вытеснения

В РИВ выполняются следующие допущения об идеальности:

1. Движущийся поток имеет плоский профиль линейных скоростей (то есть скорость движения потока в любой точке поперечного сечения реактора одинакова).

2. В любом сечении, перпендикулярном оси потока, все параметры выравнены.

3. Отсутствует перемешивание смеси в направлении оси потока.

Для реакторов непрерывного действия характерен стационарный режим работы, то есть параметры в реакторе не изменяются с течением времени.

Отсутствие перемешивания вдоль оси реактора идеального вытеснения при протекании в нем химической реакции приводит к неравномерному распределению концентраций участников реакции по длине аппарата.

Исходя из допущений об идеальности РИВ, за элементарный объем аппарата принимают бесконечно малый объем (dV_p). В качестве элементарного объема можно рассматривать объем, вырезанный в канале двумя параллельными плоскостями, находящимися друг от друга на бесконечно малом расстоянии dl и перпендикулярными оси канала. По условию стационарности в качестве элементарного промежутка времени можно принять любой промежуток времени τ.

Изменение концентрации реагента А в реакторе идеального вытеснения по длине (объему) реактора и во времени в любой точке реактора

Следует отметить, что допущения об идеальности в реальных реакторах не выполняются. Из гидравлики известно, что даже очень гладкие каналы оказывают гидравлическое сопротивление движению потока. Наличие сопротивления движению приводит к уменьшению скорости движения потока от центра канала к стенкам.

Профили линейных скоростей потока при ламинарном, развитом турбулентном и идеальном режимах течения жидкости

Сравнивая профили скоростей при различных потоках, видим, что максимально приблизиться к идеальному вытеснению можно лишь в развитом турбулентном режиме. Однако турбулентный поток характеризуется наличием нерегулярных пульсаций, носящих хаотичный характер, в результате чего некоторые частицы потока могут опережать основной поток или отставать от него, т. е. произойдет частичное перемешивание в осевом направлении. Конечно, абсолютные значения таких перемещений будут невелики по сравнению с основным осевым перемещением потока и при больших линейных скоростях ими можно пренебречь. В то же время турбулентные пульсации в радиальном направлении будут способствовать локальному перемешиванию реагентов в сечении.

В реальном реакторе можно приблизиться к режиму идеального вытеснения, если:
1) реакционный поток — турбулентный;
2) длина канала существенно превышает его поперечный размер (например, для цилиндрических труб L/D > 20).

Материальный баланс РИВ

Материальный баланс показывает изменение количества реагента или продукта за счёт его поступления (со знаком плюс) и расходования (со знаком минус) в элементарном объёме за элементарный промежуток времени.

Запишем материальный баланс РИВ по взятому в недостатке реагенту A:

Здесь N_Aвх − количество (в молях) реагента A, поступающего со входящим в элементарный объём потоком реакционной массы за элементарный промежуток времени,

N_Aвых − количество (в молях) реагента A, уходящего с выходящим из элементарного объёма потоком реакционной массы за элементарный промежуток времени,

N_Aх.р − количество (в молях) реагента A, расходуемого на протекание химической реакции в элементарном объёме за элементарный промежуток времени.

Входящие в состав материального баланса РИС-Н слагаемые могут быть выражены через параметры процесса следующим образом:

(здесь C_A − концентрация реагента A на входе в элементарный объём, V_o − объёмный расход реакционной смеси,τ − элементарный промежуток времени)

(здесь dC_A − изменение концентрации реагента A в элементарном объёме, V_o − объёмный расход реакционной смеси, τ − элементарный промежуток времени)

(здесь W_A − скорость химической реакции по компоненту A, dV_р − элементарный объём, τ − элементарный промежуток времени)

При подстановке полученных выражений в уравнение материального баланса РИВ получим:

Преобразуем выражение, сократив на элементарный промежуток времени τ, и вынеся за скобку объёмный расход смеси V_o:

Отношение элементарного объёма dV_р к объёмному расходу реакционной смеси V_o соответствует полному времени пребывания частиц в элементарном объёме (для сохранения аналогии с РИС-Н будем называть его средним временем пребывания):

Выразив среднее время пребывания частиц в элементарном объёме, получим дифференциальную форму характеристического уравнения РИВ:

Проинтегрировав на интервале от 0 до , рассчитаем среднее время пребывания частиц в РИВ:

Учитывая, что , получаем характеристическое уравнение РИВ:

Тепловой баланс РИВ

Тепловой баланс показывает изменение количества теплоты за счёт её поступления (со знаком плюс) и расходования (со знаком минус) в элементарном объёме за элементарный промежуток времени.

Запишем тепловой баланс политермического РИВ:

Здесь Q_вх − количество теплоты, поступающей со входящим в элементарный объём потоком реакционной массы за элементарный промежуток времени,

Q_вых − количество теплоты, уходящей с выходящим из элементарного объёма потоком реакционной массы за элементарный промежуток времени,

Q_х.р − количество теплоты, выделяющейся (со знаком плюс) или поглощаемой (со знаком минус) при протекании химической реакции в элементарном объёме за элементарный промежуток времени,

Q_т.о − количество теплоты, вносимой (со знаком плюс) в элементарный объём или отводимой (со знаком минус) из него за счёт теплообмена с теплоносителем или хладагентом за элементарный промежуток времени.

Входящие в состав теплового баланса РИВ слагаемые могут быть выражены через параметры процесса следующим образом:

(здесь ρ_o − плотность входящей в элементарный объём реакционной смеси, V_o − объёмный расход реакционной смеси, c_po − удельная теплоёмкость входящей в элементарный объём реакционной смеси,T − температура входящей в элементарный объём реакционной смеси, τ − элементарный промежуток времени),

(здесь ρ − плотность выходящей из элементарного объёма реакционной смеси, V_o − объёмный расход реакционной смеси, c_p − удельная теплоёмкость выходящей из элементарного объёма реакционной смеси, (T+dT) − температура выходящей из элементарного объёма реакционной смеси, τ − элементарный промежуток времени)

(здесь ΔH − тепловой эффект химической реакции, W_A − скорость химической реакции по компоненту A, dV_р − элементарный объём,τ − элементарный промежуток времени)

(здесь K_т − коэффициент теплопередачи между теплоносителем или хладагентом и реакционной массой, dF − поверхность теплообмена между теплоносителем или хладагентом и элементарным объёмом,ΔT − положительная разность температур между теплоносителем или хладагентом и реакционной массой, τ − элементарный промежуток времени).

При подстановке полученных выражений в уравнение теплового баланса РИВ получим:

Преобразуем выражение, сократив на элементарный промежуток времени τ, и предполагая, что плотность и теплоёмкость реакционной смеси слабо зависят от температуры (ρ_oc_po ≈ ρc_p):

Выразим из материального баланса РИВ скорость реакции W_A:

Подставим это выражение в тепловой баланс и разделим все слагаемые на C_AoV_o:

Учитывая, что мольная теплоёмкость с ‘ _p может быть рассчитана по формуле , получим конечное выражение теплового баланса для политермического РИВ:

В случае адиабатического теплового режима, характеризующегося отсутствием теплообмена реакционной смеси с теплоносителем или хладагентом (тепловая изоляция реактора), тепловой баланс РИВ примет вид:

=> вся теплота, выделяемая или поглощаемая в ходе химической реакции, идёт на изменение температуры реакционной смеси.

В случае изотермического теплового режима, характеризующегося постоянством температуры реакционной смеси, можно принять Q_вх ≈ Q_вых:

=> вся теплота, выделяемая или поглощаемая в ходе химической реакции, компенсируется теплообменом с хладагентом или теплоносителем.

Расчёт изотермического РИВ

Расчёт изотермического РИВ сводится к нахождению его объёма из уравнения материального баланса. Объём проточного реактора может быть рассчитан по уравнению:

Среднее время пребывания частиц в реакторе рассчитывается по характеристическому уравнению РИВ:

Скорость реакции W_A можно выразить через кинетическое уравнение:

(здесь k – константа скорости реакции, C_A и C_B – концентрации реагентов A и B, n и m – порядки реакции по компонентам A и B)

Для реакций, протекающих в газовой фазе с изменением объёма, текущая концентрация C_A реагента A может быть рассчитана по уравнению:

(здесь N_A – количество (в молях) реагента A в объёме выходящего из реактора за единицу времени потока реакционной массы, N_Ao – количество (в молях) реагента A в объёме входящего в реактор за единицу времени потока реакционной массы, V – объёмный расход реакционной смеси на выходе из реактора, ε_A – коэффициент, учитывающий изменение объёма в ходе реакции)

Коэффициент, учитывающий изменение объёма в ходе реакцииε_A рассчитывается по формуле:

(здесь Δν – изменение количества моль газообразных реагентов в ходе реакции, n_Ao – объёмная доля реагента A в исходной смеси, a – стехиометрический коэффициент перед реагентом A в уравнении химической реакции)

При описании модельной газовой реакции вида изменение количества моль газообразных реагентов в ходе реакции Δν находят следующим образом:

Для реакций, протекающих в жидкой фазе, или в газовой фазе без изменения объёма, текущая концентрация C_A реагента A может быть рассчитана по уравнению:

Для реакций, протекающих в газовой фазе с изменением объёма, текущая концентрация C_B реагента B может быть рассчитана по уравнению:

(здесь N_B – количество (в молях) реагента B в объёме выходящего из реактора за единицу времени потока реакционной массы, N_Bo – количество (в молях) реагента B в объёме входящего в реактор за единицу времени потока реакционной массы, V – объёмный расход реакционной смеси на выходе из реактора, a и b – стехиометрические коэффициенты перед реагентами A и B в уравнении химической реакции, ε_A – коэффициент, учитывающий изменение объёма в ходе реакции)

Для реакций, протекающих в жидкой фазе, или в газовой фазе без изменения объёма, текущая концентрация C_B реагента B может быть рассчитана по уравнению:

После подстановки выражений для C_A и C_B в кинетическое уравнение получим:

Тогда среднее время пребывания частиц в реакторе рассчитывается по формуле:

Конечное выражение для расчёта объёма РИВ примет вид:

Видео:РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать

Уравнение материального баланса рив в реакторе вывод. Реактор идеального вытеснения (РИВ). Способы его осуществления

В РИС все параметры по объему постоянны.

Все характеристики (концентрация С A , степень превращения Х А, температура Т и др.) изменяются плавно по объему реактора, поэтому материальный баланс для всего объема реактора составить нельзя.

Рис. 2. Графики зависимостей:

а) С А =f (τ или H) б) w= f (τ или H) в) Х А = f (τ или H)

— скорость процесса к единице объема

Пусть простая необратимая реакция протекает в реакторе без изменения объема υ:

где ,С А — соответственно начальная и текущая концентрации ;

υ- объемный расход

где V- объем реактора (м 3);

dV- элементарный объем реактора (м 3).

(Приход)

— Уравнение мат. баланса

элементарного объема РИВ-Н

— Характеристическое уравнение РИВ-Н.

где w A находим, зная кинетику процесса.

Характеристическое уравнение РИВ-Н позволяет, зная кинетику процесса

(для нахождения w А), определить время τ пребывания реагентов в реакторе доля достижения заданной степени превращения Х А , а затем — и размеры реактора.

где п — порядок реакции.

Зависит только от степени превращения Х А и не зависит от начальной концентрации ;

В некоторых производственных реакторах степень превращения Х А столь незначительна, что для расчета можно применить модель РИВ — это трубчатые контактные аппараты с катализатором в трубах или межтрубном пространстве («кожухотрубчатые»), служащие для гетерогенных газофазных реакций.

Видео:ОВР и Метод Электронного Баланса — Быстрая Подготовка к ЕГЭ по ХимииСкачать

Характеристические уравнения идеальных типов изотермических реакторов

Видео:Основы теплотехники. Реальные газы. Уравнение Ван дер Ваальса. Решение задач.Скачать

из «Реакторы в химической промышленности»

Материальный баланс – это равенство прихода и расхода вещества в реакторе или в процессе. Теоретической основой составления материальных балансов является закон сохранения материи М.И. Ломоносова.

Составим материальный баланс реактора, в котором протекает простая необратимая реакция А → С.

Масса реагента, поступающего в реактор, в единицу времени, равно массе реагента А, расходуемому в реакторе в единицу времени.

m А приход = m Арасход

Реагент А расходуется на химическую реакцию, часть реагента выходит из реактора, часть – остается в реакционном объеме в неизменном виде (накапливается).

m Арасход = m А хим.р. + m А сток + m А накопл.

m А приход = m А хим.р. + m А сток + m А накопл.

m А приход — m А сток = m А хим.р. + m А накопл.

Обозначим m А приход -m А сток =m А конвек. – масса реагента А, переносимого за счет конвекции (потоком реакционной массы).

Тогда m А накопл. =m А конвек. -m А хим.р.

Масса реагента А, остающееся неизменным в реакционном потоке, равно разнице между массой вещества А, переносимым конвективным потоком, и массой вещества А, израсходованным на химическую реакцию. Это есть уравнение материального баланса в общем виде .

Когда концентрация реагента непостоянна в различных точках объема реактора или во времени, нельзя составлять материальный баланс в общем виде, для всего объема реактора. В этом случае составляют материальный баланс для элементарного объема реактора.

Основой этого материального баланса является уравнение конвективного переноса (см. Амелин и др. с.71-73).

где С А – концентрация реагента А в реакционной смеси;

x,y,z – пространственные координаты;

W x , W y , W z – составляющие скорости потока;

D – коэффициент диффузии;

r A – скорость химической реакции.

Член характеризует изменение концентрации реагента А во времени в элементарном объеме и соответствуетm А накопл. в общем уравнении материального баланса.

Член
отражает изменение концентрации реагента вследствие переноса его в направлении, совпадающим с направлением общего потока.

Член
отражает изменение концентрации реагента А в элементарном объеме в результате переноса его путем диффузии. Вместе эти члены характеризуют суммарный перенос вещества в движущейся среде путем конвекции и диффузии; в общем уравнение материального баланса им соответствует членm А конвек. .

Член r A показывает изменение концентрации реагента А в элементарном объеме за счет химической реакции. Ему соответствует член m А хим.р. в общем уравнении материального баланса.

Полученное дифференциальное уравнение очень сложно в решении. В зависимости от типа реактора и режима его работы оно может быть преобразовано и упрощено.

Видео:Построение ИТК, расчет материального балансаСкачать

Лекция № 12 Гидродинамические модели реакторов. Вывод характеристических уравнений.

Ранее мы рассмотрели основные модели химических процессов и их математическое описание. Усложним модель химико-технологического процесса за счет учета гидродинамических процессов, то есть способов направленного движения потоков реакционной смеси в реакторе.

Любой реактор, используемый в химическом производстве. В большем или меньшем приближении можно описать одной из следующих моделей:

реактор идеального смешения периодического действия РИС-П;

реактор идеального смешения непрерывного действия РИС-Н;

реактор идеального вытеснения непрерывного действия РИВ-Н;

каскад реакторов идеального смешения непрерывного действия К-РИВ-Н (ячеечная модель).

Для каждой модели выведено характеристическое уравнение , которое выражает зависимость времени пребывания реагентов в реакторе о, начальной концентрации реагента, величины конверсии и скорости химической реакции.

τ = f (C A 0 , α A , r A)

Это уравнение является математическим описанием модели реактора . Оно дает возможность, задав С А0 (состав исходной смеси) и r A (тип химической реакции, температуру, давление, катализатор и т.п.) рассчитать время пребывания реагентов в реакторе, необходимое для достижения заданной конверсии (α A), а значит, и объем реактора, его габаритные размеры и производительность. Сравнивая полученные значения для реакторов разного типа, можно выбрать самый оптимальный вариант для проведения данной химической реакции.

Основанием для вывода характеристического уравнения является материальный баланс реактора, составленный по одному их компонентов реакционной смеси.

Реактор идеального смешения периодического действия

РИС-П представляет собой аппарат с мешалкой, в который периодически загружают исходные реагенты и также периодически выгружают продукты.

В таком реакторе создается такое интенсивное перемешивание, что в каждый момент времени концентрация реагентов одинакова по всему объему реактора и изменяется лишь во времени, по мере протекания химической реакции.

Исходным уравнением для получения характеристического уравнения является уравнение материального баланса в дифференциальной форме:

Так как вследствие интенсивного перемешивания все параметры одинаковы по всему объему реактора, в любой момент времени производная любого порядка от концентрации по осям x,y,z равна нулю.

Тогда

При V реакци.смеси = const C A = C A 0 (1-α А).

— характеристическое уравнение РИС-П

Если в реакторе протекает простая необратимая реакция «n»-го порядка, то

При n = 0
,

n = 1
.

При n ≠ 0 и 1 определение τ производят методом графического интегрирования. Для этого строят графическую зависимость

вычисляют площадь под кривой между начальным и конечным значением степени превращения.

Общее уравнение теплового баланса химического реактора. Уравнение теплового баланса для химических реакторов, работающих в изотермическом, адиабатическом и промежуточных тепловых режимов. Тепловая устойчивость химических реакторов в случае экзо- и эндо- термических реакций. Реактор с обратимой реакцией.

В уравнении теплового баланса учитываются все тепловые потоки, входящие в реактор и выходящие из него. Такими потоками являются: Q вх – физическая теплота реакционной смеси, входящей в элементарный объём для которого составляется баланс (входной поток); Q вых – физическая теплота реакционной, покидающей элементарный объём (выходной поток); Q р – теплота химической реакции (знак может быть положительным и отрицательным); Q т.о – теплота, расходуемая на теплообмен с окружающей средой (в зависимости от соотношений температур в реакторе и в окружающей среде или в теплообменном устройстве этот поток также может быть направлен и в объём и из него); Q ф.пр – теплота фазовых превращений.

Для стационарного режима работы реактора алгебраическая сумма всех тепловых потоков равна нулю: Q вх — Q вых ± Q р ± Q т.о ± Q ф.пр = 0 (1)

В нестационарном режиме происходит положительное или отрицательное накопление теплоты в элементарном объёме:

Q вх — Q вых ± Q р ± Q т.о ± Q ф.пр = Q нак (2)

Уравнения (1) и (2) являются общими уравнениями теплового баланса химического реактора. Различают несколько видов тепловых режимов химических реакций и соответственно конкретных видов уравнений теплового баланса

I. Изотермический – режим, характеризующийся тем, что температура на входе, внутри и на выходе одинакова. Это возможно, если выделение и поглощение теплоты в результате химической реакции компенсируется теплообменом с окружающей средой. Для стационарного изотермического процесса при постоянстве физических свойств системы можно записать: Q вх =Q вых; | Q р |=| Q т.о | .

Кроме принципиально изотермических реакторов смешения к изотермическому могут приближаться реакторы с весьма малым значением Q р, С А0 или х (степени превращения) при значительной теплопроводности в реакционной смеси. При моделировании реакторов к полностью изотермическим относятся реакторы различного вида, перемешивания жидкостного типа (Ж, Ж-Ж, Ж-Т). Изотермический режим наблюдается на полке пенного и барботажного аппаратов небольшого размера, а также в кипящем слое зернистого материала, и других аппаратах.

Характеристическое уравнение изотермического реактора: t ср =t к =const.

II. Адиабатический режим характеризуется полным отсутствием теплообмена с окружающей средой. В этом случае вся теплота химической реакции расходуется на нагрев или охлаждение реакционной смеси. Для стационарного процесса |Q вх -Q вых |=|Q р |. Изменение температуры в адиабатическом реакторе ∆t прямо пропорционально степени превращения х, концентрации основного реагента С А0 , тепловому эффекту реакции Q р. Изменение температуры положительно для экзотермических и отрицательно для эндотермических реакций. Уравнение теплового баланса для реакции А→В будет: G c t k ± GQ p C A 0 x=G c t k (2), отсюда получим характеристическое уравнение: ± GQ p C A 0 x=с (t k – t н) (2’).

Изменение температуры на любом участке по оси потока в реакторе идеального вытеснения пропорционально степени превращения: ∆t= t k – t н =±λх, где λ-коэффициент адиабатического изменения температуры: λ=(Q p * C D)/c, где

C D – концентрация продукта. Уравнение теплового баланса для элементарного участка реактора будет: ±Q p C A dx A =cdt (3) . Для реактора полного смешения уравнение теплового баланса такое же как (2’).

III. Промежуточный (политропный или автотермический) режим характеризуется тем, что частично теплота реакции расходуется на изменение теплосодержания (нагрев или охлаждение) реакционной смеси, а частично на теплообмен с окружающей средой. Этот режим наиболее часто встречается в ТХП. Этот режим описывается полным уравнением теплового баланса. При неизменной весовой теплоёмкости и установившемся режиме тепло, выделившееся (поглощенное) в результате реакции при степени превращения х А будет унесено продуктами реакции и передано через стенку реактора: ±GQ p C A 0 x А =G c (t k – t н) ± k т F∆t ср (4),отсюда может быть найдено: 1)изменение температуры (t k – t н), степень превращения (х А), поверхность теплопередачи (F). Это уравнение (4) получено для реактора смешения и для реактора вытеснения , в котором температура одинакова по всей длине, то есть температура теплоносителя или охлаждающего агента, находящихся в рубашке, постоянна по всей длине реактора; температура реагентов одинакова в любой точке поперечного сечения реактора. Так как температура в реакторе изменяется по его длине, тепловой баланс составляется для элементарного участка длины реактора (∆Н): GQ p C A 0 x А =G c dt± k т F’(t-t окр)dH; где t – температура в рассматриваемом элементе реактора; t окр – температура в рубашке.

Сравнение характеристик изотермических, адиабатических и политермических процессов приведено на рисунках.

Устойчивость работы реактора – одно из требований, которые предъявляются к ним. Согласно А. М. Ляпунову “Система называется устойчивой, если после наложения какого-либо возмущения она возвращается в прежнее состояние при снятии этого возмущения”.

Наиболее важной является температурная (тепловая) устойчивость химических реакций и реакторов. При экзо- и эндо- термических реакциях происходит авторегулировка температуры технологического процесса за счёт влияния концентрации реагентов химического процесса. В некоторых случаях при – образной форме зависимости количества выделяемого тепла от температуры в реакторе полного слияния при обратимой экзотермической реакции.

Устойчивость технологического режима реактора можно определить по его чувствительности при изменении того или иного параметра и называется параметрической чувствительностью: П=dy/dx, где у – входная величина – параметр (температура, расход реагентов, концентрация), х – выходная величина – параметр, характеризующий результат процесса (степень превращения, температура, время реакции).