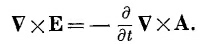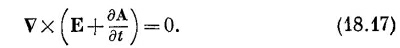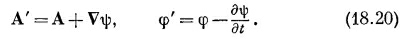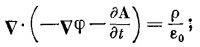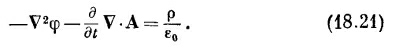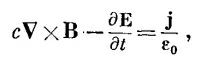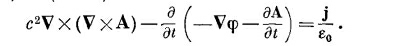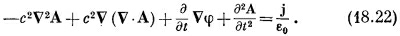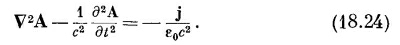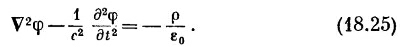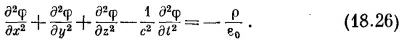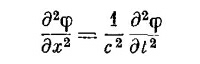Про уравнения - легко » Статьи

Уравнения максвелла примеры решения задач

Обновлено
Содержание
  1. 9.3. Уравнения Максвелла
  2. Система уравнений Максвелла
  3. Решение уравнений Максвелла; потенциалы и волновое уравнение
  4. 📹 Видео

Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.

9.3. Уравнения Максвелла

Четыре уравнения, соответствующие нашим (модифицированным) утверждениям, называются уравнениями Максвелла в интегральной форме.

Выпишем их все рядом еще раз:

Уравнения максвелла примеры решения задач

Чтобы получить уравнения Максвелла в среде, надо произвести замену:

Уравнения максвелла примеры решения задач,

то есть указать связь (так называемые «материальные» уравнения) между напряженностями и индукциями: Уравнения максвелла примеры решения задачи Уравнения максвелла примеры решения задачи дополнить систему уравнением закона Ома

Уравнения максвелла примеры решения задач.

Отметим, что приведенными выше простейшими соотношениями можно пользоваться не всегда. Ситуация заметно сложнее в присутствии таких веществ как сегнетоэлектрики, пьезоэлектрики, ферромагнетики, вещества анизотропные и тому подобное. Здесь наша цель показать, как формируется полная система уравнений, позволяющая (с учетом начальных и граничных условий, разумеется) рассчитать электромагнитное поле.

От уравнений в интегральной форме можно с помощью теорем векторного анализа перейти к уравнениям в дифференциальной форме, связывающим значения полей Уравнения максвелла примеры решения задачи Уравнения максвелла примеры решения задачи их пространственных и временных производных со значениями плотностей заряда и тока. Этими уравнениями мы пользоваться не будем, но все же приведем их хотя бы как часть шутки, опубликованной в одном из журналов в дни юбилея Максвелла:

Уравнения максвелла примеры решения задач

Непонятные значки div (читается «дивергенция») и rot (читается «ротор») — это особые операции дифференцирования, выполняемые над векторными полями. Дивергенция — по латыни «расхождение». Эта операция описывает конфигурацию силовых линий типа «ежа», расходящихся из точек, где имеются электрические заряды. Слово «ротор» в переводе не нуждается, оно явно ассоциируется с вращением. Эта операция описывает вихревые поля (кольцеобразные — замкнутые силовые линии) вокруг их источников — токов или других полей, меняющихся во времени.

Четыре интегральных уравнения и четыре дифференциальных эквивалентны. Максвелл показал, что все явления электромагнетизма можно полностью описать этими четырьмя уравнениями, являющимися обобщением экспериментальных фактов.

В приведенной шутке упоминался свет. Действительно, свет — это электромагнитное излучение определенного диапазона частот. Предсказание электромагнитных волн стало одним из величайших достижений теории Максвелла. Представим себе, что заряды и токи отсутствуют. Посмотрим на уравнения Максвелла в дифференциальной форме. Видно, что если поля не статические, но зависят от времени, то имеется вихревое электрическое и магнитные поля (соответствующие роторы отличны от нуля). Распространение полей без зарядов и токов — это и есть электромагнитные волны. И можно углядеть в уравнениях намек на скорость их распространения: туда входит комбинация e0m0, через которую может быть выражена скорость света в вакууме (см. (6.3))

Уравнения максвелла примеры решения задач

Но об этом — позже, в следующей части нашего курса.

В заключение же этой части процитируем слова Г. Герца об уравнениях Максвелла:

«Трудно избавиться от чувства, что эти математические формулы живут независимой жизнью и обладают своим собственным интеллектом, что они мудрее, чем мы сами, мудрее даже, чем их первооткрыватели, и что мы извлекаем из них больше, чем было заложено в них первоначально».

Пример использования уравнений Максвелла

Определить величину магнитного поля в зазоре конденсатора как функцию r расстояния от оси симметрии (рис. 9.13)

Уравнения максвелла примеры решения задач

Рис. 9.13. Конденсатор с круглыми пластинами в процессе зарядки

Решение

Запишем уравнение (9.13) для контура, показанного на Рис. 9.3 штрихованной линией. Интегрируя, получим

Уравнения максвелла примеры решения задач

Уравнения максвелла примеры решения задач

Очевидно, что магнитное поле не равно нулю только благодаря наличию меняющегося со временем электрического поля. В свою очередь, изменение электрического поля обусловлено увеличением заряда на обкладках конденсатора. Эту связь получим из соотношений

Уравнения максвелла примеры решения задач

Уравнения максвелла примеры решения задач

Согласно полученной формуле,

Уравнения максвелла примеры решения задач

что явно неверно. В чем ошибка?

ОТВЕТ: формула справедлива только при Уравнения максвелла примеры решения задач.

Дополнительная информация

Видео:Билеты №32, 33 "Уравнения Максвелла"Скачать

Билеты №32, 33 "Уравнения Максвелла"

Система уравнений Максвелла

Первое уравнение Максвелла в интегральной формеявляется обобщением закона электромагнитной индукции Фарадея в форме

Уравнения максвелла примеры решения задач.

Согласно Максвеллу этот закон справедлив не только для проводящего контура, но и для любого замкнутого контура, мысленно выбранного в переменном магнитном поле. Иными словами, с переменным магнитным полем независимо от того, находятся в нём проводники или нет, неразрывно связано вихревое электрическое поле.

Переменное электрическое поле, так же как и электрический ток, является источником магнитного поля. Количественной мерой магнитного действия переменного электрического поля служит ток смещения. Плотностью тока смещенияназывается вектор:

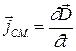
Уравнения максвелла примеры решения задач.

Уравнения максвелла примеры решения задачВторое уравнение Максвелла в интегральнойформе: циркуляция вектора напряжённости магнитного поля по произвольному контуру L равна алгебраической сумме макротоков и тока смещения сквозь поверхность, натянутую на этот контур (рис. 2.21) и находится по формуле

Уравнения максвелла примеры решения задач,

где Уравнения максвелла примеры решения задач— плотность тока проводимости; IСМ.— ток смещения.

Третье уравнение Максвелла в интегральной форме

Уравнения максвелла примеры решения задач,

где r — объемная плотность свободных электрических зарядов.

Четвёртое уравнение Максвелла в интегральной форме

Уравнения максвелла примеры решения задач.

Систему уравнений Максвелла необходимо дополнить так называемыми материальными уравнениями, характеризующими электрические и магнитные свойства среды.

В случае изотропных несегнетоэлектрических и неферромагнитных сред и макротоков, подчиняющихся закону Ома, эти уравнения имеют вид

Уравнения максвелла примеры решения задач, Уравнения максвелла примеры решения задач, Уравнения максвелла примеры решения задач,

где e0, m0 — электрическая и магнитная постоянные; e, m — относительные диэлектрическая и магнитная проницаемости среды; s — удельная электрическая проводимость среды.

Примеры решения задач

1. Квадратная рамка со стороной а=2 см, содержащая 100 витков, подвешена на упругой нити с постоянной кручения С=10 мкН×м/град. Плоскость рамки совпадает с направлением линий индукции внешнего магнитного поля. Определить индукцию магнитного поля, если при пропускании по рамке тока I=1А она повернулась на угол j=60 о .

Решение

Уравнения максвелла примеры решения задач Уравнения максвелла примеры решения задачРамка будет находиться в равновесии, когда результирующий момент сил, действующий на рамку, равен нулю, т.е. Уравнения максвелла примеры решения задач, где М1— момент сил, действующих на рамку с током со стороны магнитного поля; М2 — момент упругих сил.

где р m = NIS = NIa 2 — магнитный момент рамки; В — индукция магнитного поля; a — угол между вектором Уравнения максвелла примеры решения задачи нормалью к плоскости рамки. Как видно из рисунка, угол a=90°–j =30°.

Из условия равновесия

Ia 2 NB sin a — Сj = 0,

B = Сj/(Ia 2 NB sin a).

Подставим числовые значения:

В = 10 -3 ×60 / 1×4×100×0,5 = 30 мТл.

2. Прямой бесконечный проводник имеет круговую петлю радиусом R=80 см. Определить силу тока в проводнике, если известно, что в точке А магнитная индукция B = 12,5 мкТл.

Уравнения максвелла примеры решения задачРешение

Уравнения максвелла примеры решения задачПо принципу суперпозиции индукция магнитного поля в точке А равна векторной сумме индукций магнитных полей, созданных бесконечно длинным проводником с током I (В1) и круговым током в его центре (В2):

Уравнения максвелла примеры решения задач.

Векторы В1 и В2 на рисунке в точке А будут направлены в одну сторону перпендикулярно плоскости рисунка от нас, тогда можно записать

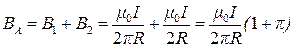
Уравнения максвелла примеры решения задач,

Уравнения максвелла примеры решения задач.

Подставим числовые значения:

Уравнения максвелла примеры решения задачА.

3. Квадратная рамка расположена в одной плоскости с длинным прямым проводником с током I0 =5 А. Сторона рамки 8 см. Проходящая через середины противоположных сторон ось рамки параллельна проводу и отстоит от него на расстоянии, которое в n = 1,5 раза больше стороны рамки. Найти поток вектора Уравнения максвелла примеры решения задаччерез поверхность рамки.

Уравнения максвелла примеры решения задач Уравнения максвелла примеры решения задачРешение

Прямой проводник с током создает вокруг себя неоднородное магнитное поле с индукцией

Уравнения максвелла примеры решения задач,

которая уменьшается с увеличением расстояния от проводника. Направление вектора индукции будет совпадать с направлением нормали к рамке. Так как магнитное поле неоднородное, поверхность, ограниченную рамкой, разобьём на элементарные площадки dS = a×dr, в пределах которых магнитную индукцию можно считать постоянной величиной (см. рисунок). Тогда поток магнитной индукции (магнитный поток) через элементарную площадку

Полный поток вектора Уравнения максвелла примеры решения задаччерез поверхность рамки

Уравнения максвелла примеры решения задач.

Подставим числовые значения:

Фm = 4p×10 –7 ×5×0,08×(ln 2)/2p = 5,545×10 –8 Вб.

Уравнения максвелла примеры решения задач4. Между полюсами электромагнита требуется создать магнитное поле с индукцией В=1,4 Тл. Длина железного сердечника l1=40 см, длина межполюсного пространства l2=1 см, диаметр сердечника D=5 см. Какую ЭДС нужно взять для питания обмотки электромагнита, чтобы получить требуемое магнитное поле, используя медную проволоку площадью поперечного сечения S=1 мм 2 ? Какая будет при этом наименьшая толщина b намотки, если считать, что предельно допустимая плотность тока j=3 МА/м 2 ?

Решение

Так как силовые линии магнитного поля замкнуты, то магнитный поток и индукция магнитного поля в сердечнике и в воздушном зазоре одинаковы: В1=В2. Для решения задачи воспользуемся теоремой о циркуляции вектора Уравнения максвелла примеры решения задач(т.к. циркуляция Уравнения максвелла примеры решения задачопределяется только макротоками и не зависит от наличия или отсутствия магнетика). Выберем замкнутый контур вдоль силовой линии и вычислим циркуляцию вектора напряжённости:

Уравнения максвелла примеры решения задач,

где Н1 и Н2 — напряжённости магнитного поля в сердечнике и вне его; l1 и l2 – длина железного сердечника и межполюсного пространства.

Поскольку величина В1 известна по условию задачи, то величину Н1 найдём из графика зависимости В = В(H) (прил. 1):

при В = 1,3 Тл, Н = 800 А/м.

Из уравнения (1) определим число ампер-витков электромагнита:

(NI) = 800×0,4 + 1,3×0,01/(4×3,14×10 –7 ) = 1,07×10 4 А-вит.

Величину ЭДС e вычислим по закону Ома:

e=IRпров = Irl пров/S = IrpDN / S = IrpDN / S.

Подставим числовые значения:

e = 1,7×10 –8 ×3,14×0,05×1,07×10 4 /10 –6 = 29 В.

Для определения толщины обмотки нужно знать общее число витков N и число витков N1 в одном слое обмотки.

где l1 – длина сердечника; d – диаметр провода обмотки: d = Уравнения максвелла примеры решения задач, тогда

N1 = l1/ Уравнения максвелла примеры решения задач= 0.4 / Уравнения максвелла примеры решения задач= 354 витка .

Зная число ампер–витков и предельно допустимое значение силы тока (I=jS), определим общее число витков N

N = (NI)/(jS) = 1,07×10 4 / (3×10 6 ×10 –6 ) = 3567 витков.

Тогда толщина обмотки

b = d×k = k× Уравнения максвелла примеры решения задач= 10× Уравнения максвелла примеры решения задач= 11,3×10 -3 м » 11 мм.

5. Квадратная рамка с током I=1 А расположена в одной плоскости с длинным прямым проводником с током I0=5 А. Сторона рамки 10 см. Ось рамки, проходящая через середины противоположных сторон, параллельна проводу и отстоит от него на расстоянии, которое в n = 1,5 раза больше стороны рамки. Найти:

1) силу, действующую на рамку;

2) работу, которую нужно совершить для поворота рамки вокруг её оси на 180°, если токи поддерживают неизменными.

Решение

Уравнения максвелла примеры решения задач1. Прямой длинный проводник с током I0 создаёт вокруг себя неоднородное магнитное поле с индукцией B0=m0Io/2pr, которая уменьшается с увеличением расстояния от проводника. В таком магнитном поле на каждую сторону квадратной рамки с током будет действовать сила Ампера, направление которой можно определить по правилу левой руки, а величину — по формуле FA=IB0lsin a.

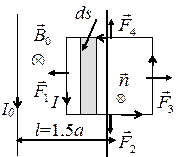
Как видно из рисунка (при указанных направлениях силы тока в проводниках), l=a, a=90° (sin a =1), силы Уравнения максвелла примеры решения задачи Уравнения максвелла примеры решения задачпротивоположны по направлению и равны по величине

Уравнения максвелла примеры решения задач Уравнения максвелла примеры решения задач.

Следовательно, результирующая этих двух сил равна нулю. Силы Уравнения максвелла примеры решения задачи Уравнения максвелла примеры решения задачпротивоположны по направлению, но не равны по величине:

Так как сила F1 в два раза больше силы F3, то результирующая этих сил будет совпадать по направлению с силой F1, а по величине

Подставим числовые значения

F = 4p×10 –7 ×1×5/4p = 5×10 –7 Н = 0,5 мкН.

2. Работу, необходимую для поворота рамки с током I на 180°, можно определить по формуле

где Ф1m и Ф2m — магнитные потоки через поверхность рамки в начальном и конечном состояниях. Так как магнитное поле проводника с током I0 неоднородное, сначала определим магнитный поток через элементарную площадку dS=adr, в пределах которой индукцию магнитного поля можно считать постоянной величиной:

а полный магнитный поток сквозь рамку в начальном и конечном состояниях

Уравнения максвелла примеры решения задач.

Уравнения максвелла примеры решения задач.

Подставим числовые значения:

А = –4p×0,1×1×5×0,69×10 –7 /p » –1,4×10 –7 Дж = –0,14 мкДж .

6. Тонкий металлический стержень длиной l = 1,2 м вращается в однородном магнитном поле вокруг перпендикулярной к стержню оси, отстоящей от одного из его концов на расстоянии а=0,25 м, делая n=120 об/мин. Вектор магнитной индукции поля параллелен оси вращения и имеет величину В=10 –3 Тл. Найти разность потенциалов U, возникающую между концами стержня.

Решение

Уравнения максвелла примеры решения задач Уравнения максвелла примеры решения задачРазность потенциалов между концами стержня будет равна по величине ЭДС индукции, возникающей в стержне за счёт вращения

Уравнения максвелла примеры решения задач. (1)

Для однородного магнитного поля и плоской поверхности dФm=BdScosa, или, подставив в (1), получаем (знак минус опустим, так как необходимо найти только величину ЭДС)

Уравнения максвелла примеры решения задач. (2)

По условию задачи cosa =1, поэтому из выражения (2) следует

Уравнения максвелла примеры решения задач, (3)

dj = wdt = (2pn)dt. (4)

Подставляя (4) в (3), получим:

Уравнения максвелла примеры решения задач.

U = 10 –3 ×2p×2 (1,2 2 + 2×1,2×0,25)/2 = 0,0128 В = 12,8 мВ.

7. Прямой проводник длиной l=10 см помещён в однородное магнитное поле с индукцией В=1 Тл. Концы проводника замкнуты гибким проводом, находящимся вне поля. Сопротивление внешней цепи R=0,4 Ом. Какая мощность потребуется для того, чтобы двигать проводник перпендикулярно линиям индукции с постоянной скоростью u=20 м/с?

Уравнения максвелла примеры решения задачРешение

Проведём анализ условия задачи. При движении проводник будет пересекать линии индукции. За счёт этого в проводнике возникнет ЭДС индукции

где в данном случае

dФ = BdS = Bludt . (2)

Подставляя (2) в (1), получаем:

Сила индукционного тока в цепи согласно закону Ома

Тепловая мощность, выделяемая на внешнем сопротивлении

P = I 2 R = B 2 l 2 u 2 /R.

Эта мощность будет равна мощности, которую необходимо подводить к системе за счёт внешней силы, действующей на проводник, для того, чтобы скорость движения проводника была постоянной. Таким образом:

P = B 2 l 2 u 2 /R = 1×0,01×400/0,4 = 10 Вт.

8. Две катушки равномерно намотаны на цилиндрический сердечник, длина которого много больше диаметра. Индуктивность первой катушки 0,2 Гн, второй- 0,8 Гн. Сопротивление второй катушки 600 Ом. Какой ток потечёт по второй катушке, если ток в 0,3 А, текущий в первой катушке, выключить в течение времени 0,001 с.

Уравнения максвелла примеры решения задачРешение

Данная задача относится к разделу взаимной индукции. Сила тока во вторичной обмотке

Величина e2 зависит от взаимной индуктивности L12 и быстроты изменения силы тока I1

Взаимная индуктивность двух соленоидов, имеющих общий сердечник, рассчитывается по формуле

поэтому, учитывая выражения (3), (4), (5), получаем

L12 = Уравнения максвелла примеры решения задач. (6)

Подставляя выражение (6) в выражение (2), а полученный результат — в выражение (1), получаем:

I2 = (L12I 01)/R2 = (I01 Уравнения максвелла примеры решения задач)/R2Dt.

I2 = Уравнения максвелла примеры решения задач= 0,2 А.

9. На тороид квадратного поперечного сечения намотано 1000 витков провода. Внутренний радиус тороида равен 0,1 см, внешний — 0,2 см. Магнитная проницаемость тороида равна100. По обмотке тороида протекает электрический ток силой 1 À. Определить энергию магнитного поля внутри тороида.

Уравнения максвелла примеры решения задачРешение

Решим задачу двумя способами.

1. Энергия магнитного поля – это энергия, запасённая в индуктивности:

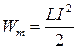
Уравнения максвелла примеры решения задач,

где L — индуктивность, I — сила тока, протекающего в индуктивности.

Потокосцепление, согласно определению индуктивности, рассчитывается как

где Фm — магнитный поток через поперечное сечение S тороида.

Уравнения максвелла примеры решения задач,

где r — расстояние от центра тороида до площадки dS, на которой определяется величина индукции магнитного поля. Так как тороид квадратного сечения, то высота площадки h = (r 2 — r 1), а ширина — dr. Поэтому

Уравнения максвелла примеры решения задач.

Тогда индуктивность тороида

L = 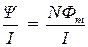Уравнения максвелла примеры решения задач= Уравнения максвелла примеры решения задачmm0N 2 (r2 — r1)ln Уравнения максвелла примеры решения задач.

Подставляя выражение для индуктивности в выражение для энергии, получаем

Уравнения максвелла примеры решения задач.

Wm = 100×4p×10 –7 ×10 6 ×10 –3 ×1×ln2 /(4p) = 6,9 мДж.

2. Энергия магнитного поля Wm связана с плотностью энергии wm соотношением:

Wm = Уравнения максвелла примеры решения задач,

Выберем в качестве элемента объема dV объем цилиндрического слоя радиусом r, высотой h=(r2 — r1) и толщиной dr (в пределах этого слоя величина Н постоянна). Запишем выражение для dV=(r2 – r1)2pr·dr и подставим в выражение для энергии Wm. Получаем

W m = 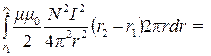Уравнения максвелла примеры решения задач Уравнения максвелла примеры решения задачmm 0N 2 I 2 (r 2 — r 1)ln Уравнения максвелла примеры решения задач.

Подставим числовые значения и получим:

Как видим, оба решения дают одно и то же значение.

Примечание: если в условии задачи величина m не задана, а указано, что тороид представляет собой железный, стальной или чугунный сердечник, то величина m находится по графику зависимости В = В(Н) (прил. 1) как

В качестве величины Н принять значение Н в центральной точке поперечного сечения тороида.

Задачи для самоконтроля

Уравнения максвелла примеры решения задачДлинный провод с током I=50 А изогнут под углом a=2p/3. Определить магнитную индукцию в точке А. Расстояние d=5 см.

2. Уравнения максвелла примеры решения задачТороид с железным сердечником, длина которого по средней линии l=1 м, имеет воздушный зазор шириной l2. По обмотке тороида, содержащей N=1300 витков, пустили ток

I=2 A, в результате чего индукция в зазоре В2 стала равна 1 Тл. Определить ширину зазора l2.

3. a-частица, кинетическая энергия которой Ек=500 эВ, влетает в однородное магнитное поле, перпендикулярно к направлению её движения. Индукция магнитного поля В=0,1 Тл. Определить силу F, действующую на a-частицу, радиус R окружности, по которой движется a-частица, и период обращения Т a-частицы.

4. Квадратная рамка со стороной а=10 см, по которой течет ток I=200 А, свободно установилась в однородном магнитном поле (В=0,2 Тл). Определить работу, которую необходимо совершить при повороте рамки вокруг оси, лежащей в плоскости рамки и перпендикулярной линиям магнитной индукции, на угол j=2p/3 радиан.

Ответ: А=I·В·а 2 ·(1-cosj)=0,6 Дж.

5. Бесконечно тонкий проводник равномерно вращается с частотой n=10 об/с в однородном магнитном поле с индукцией В=0,01 Тл. Ось вращения, проходящая через один из концов проводника, параллельна линиям индукции и составляет угол a=30 о с осью проводника. Найти разность потенциалов между концами проводника, если его длина l = 0,1 м.

Ответ: Уравнения максвелла примеры решения задачВ.

6. Из провода радиусом а=1,00 мм сделана прямоугольная рамка, длина которой l=10,0 м значительно больше ширины b=0,10 м (измеренной между осями сторон рамки). Найти индуктивность рамки L. Магнитная проницаемость среды равна 1. Полем внутри проводов пренебречь.

Ответ: Уравнения максвелла примеры решения задачмкГн.

7. Две катушки расположены на небольшом расстоянии друг от друга. Когда сила тока в первой катушке изменяется с быстротой DI/Dt=5 А/с, во второй катушке возникает ЭДС индукции ei=0,1 В. Определить взаимную индуктивность катушек.

Ответ: Lвз = Уравнения максвелла примеры решения задач= 20 мГн.

8. Напряженность магнитного поля тороида со стальным сердечником возросла от Н1=200 А/м до Н2=800 А/м. Определить, во сколько раз изменилась объемная плотность энергии магнитного поля.

Ответ: Уравнения максвелла примеры решения задач.

Контрольное задание № 4

401. По двум длинным параллельным проводам текут в противоположных направлениях токи силой I1=I2=I=10 А. Расстояние между проводами d=0,3 м. Определить магнитную индукцию в точке А, удаленной от первого и второго проводов соответственно на расстояния r1=0,15 м и r2=0,2 м.

402. Определить магнитную индукцию В поля, создаваемого отрезком бесконечно длинного провода, в точке, равноудалённой от концов отрезка и находящейся на расстоянии а=4 см от его середины. Длина отрезка провода l=20 см, сила тока в проводе I=10 А.

403. Определить индукцию магнитного поля в центре проволочной квадратной рамки со стороной а=15 см, если по рамке течёт ток I=5 А.

404. Определить индукцию магнитного поля в центре контура, имеющего вид прямоугольника, если его диагональ d=16 см, угол между диагоналями j=30°, ток в контуре I=5 А.

405. Ток I=20 А течёт по длинному проводнику, согнутому под прямым углом. Определить индукцию магнитного поля в точке, лежащей на биссектрисе этого угла и отстоящей от вершины угла на 10 см.

Уравнения максвелла примеры решения задач

406. На рисунке изображены сечения двух прямолинейных бесконечно длинных проводников с токами. Расстояние между проводниками АВ=10 см, токи I1=20 А и I2=30 А. Определить индукцию В магнитного поля, вызванного токами I1 и I2 в точках М1, М2, М3. Расстояния М1А =2 см, АМ2 =4 см, ВМ3 =3 см.

Уравнения максвелла примеры решения задач407. Два прямолинейных бесконечно длинных проводника с токами расположены перпендикулярно друг к другу и находятся в одной плоскости. Определить индукцию магнитного поля в точках М1 и М2, если токи I1=2 А, I2=3 А. Расстояния АМ1 =АМ2 =1 см, ВМ1 =СМ2 =2 см.

408. Бесконечно длинный тонкий проводник с током I=50 А имеет изгиб радиусом R=10 см. Определить индукцию магнитного поля в точке О (в центре изгиба).

Уравнения максвелла примеры решения задач409. По проводу, согнутому в виде правильного шестиугольника со стороной а=20 см, течёт ток I=100 А. Определить индукцию магнитного поля в центре шестиугольника. Для сравнения определить магнитную индукцию магнитного поля в центре кругового провода, совпадающего с окружностью, описанной около данного шестиугольника.

410. Тороид с железным сердечником, длина которого по средней линии l=1 м, имеет воздушный зазор l2=3 мм. По обмотке тороида, содержащей N=1300 витков, пустили ток, в результате чего индукция в зазоре В2 стала равна 1 Тл. Определить силу тока.

411. По проводнику, изогнутому в виде окружности, течёт ток. Индукция магнитного поля в центре окружности равна 25,1 мкТл. Не изменяя силы тока в проводнике, ему придали форму квадрата. Определить индукцию магнитного поля в точке пересечения диагоналей этого квадрата.

412. Внутри соленоида длиной l=25,1 см и диаметром D=2 см помещён железный сердечник. Соленоид имеет N=200 витков. Определить магнитный поток Фm, если ток в соленоиде I=5 А.

413. Магнитная индукция В на оси тороида без сердечника (внешний диаметр тороида d1=60 см, внутренний — d2=40 см), содержащего N=200 витков, составляет 0,16 мТл. Пользуясь теоремой о циркуляции вектора Уравнения максвелла примеры решения задач, определить силу тока в обмотке тороида.

414. По прямому бесконечно длинному проводнику течёт ток I=10 А. Определить, пользуясь теоремой о циркуляции вектора Уравнения максвелла примеры решения задач, магнитную индукцию В в точке, расположенной на расстоянии r=10 см от проводника.

415. Тороид намотан на железное кольцо сечением S=5 см 2 . При силе тока I=1 А магнитный поток Фm=250 мкВб. Определить число витков n тороида, приходящихся на отрезок длиной 1 см средней линии кольца.

416. Электромагнит изготовлен в виде тороида. Сердечник тороида со средним диаметром d=51 см имеет вакуумный зазор длиной l0 =2 мм. Обмотка тороида равномерно распределена по всей его длине. Во сколько раз уменьшится индукция магнитного поля в зазоре, если, не изменяя силы тока в обмотке, зазор увеличится в n=3 раза? Рассеянием магнитного поля вблизи зазора пренебречь. Магнитную проницаемость m сердечника считать постоянной и принять равной 800.

417. Обмотка катушки сделана из проволоки диаметром d=0,8 мм. Витки плотно прилегают друг к другу. Считая катушку достаточно длинной, определить напряжённость H и индукцию B магнитного поля внутри катушки при токе I=1A.

418. Железное кольцо диаметром D=11,4 см имеет обмотку из N=200 витков, по которой течет ток I1=15A. Какой ток I2 должен проходить через обмотку, чтобы индукция в сердечнике осталась прежней, если в кольце сделать зазор шириной b=1 мм? Определить магнитную проницаемость m материала сердечника при этих условиях.

419. Обмотка соленоида состоит из N витков медной проволоки, поперечное сечение которой S=1 мм 2 . Длина соленоида l=25 см, диаметр D=5 см. Определить напряженность H и индукцию B магнитного поля внутри соленоида при токе I=2 A, если сопротивление соленоида R=0,2 Ом. Удельное сопротивление меди r=17·10­­­ -9 Ом·м.

420. Внутри соленоида с числом витков N=200 с никелевым сердечником (m=200) напряженность однородного магнитного поля H=10 кA/м. Площадь поперечного сечения сердечника S=10 см 2 . Определить: 1) магнитную индукцию поля внутри соленоида; 2) потокосцепление.

421. По двум тонким проводам, изогнутым в виде колец радиусом R=10 см, текут одинаковые токи I=10 А в каждом. Найти силу взаимодействия этих колец, если плоскости, в которых лежат кольца, параллельны, а расстояние d между центрами колец равно 1мм.

422. Виток, диаметр которого d=20 см, может вращаться около вертикальной оси, совпадающей с одним из диаметров витка. Виток установили в плоскости магнитного меридиана и пустили по нему ток I=10 A. Какой вращающий момент нужно приложить к витку, чтобы удержать его в начальном положении? Горизонтальную составляющую Bг магнитной индукции поля Земли принять равной 20 мкТл.

423. Из проволоки длинной l=20 см сделаны квадратный и круговой контуры. Определить вращающие моменты сил M1 и M2, действующие на каждый контур, помещенный в однородное магнитное поле с индукцией В=0,1 Тл. По контурам течет ток I=2 A. Плоскость каждого контура составляет угол a=45° с направлением поля.

424. Электрон, ускоренный разностью потенциалов U=0,5 кВ, движется параллельно прямолинейному длинному проводнику на расстоянии r=1 см от него. Определить силу, действующую на электрон, если через проводник пропускать ток I=10 А.

425. Электрон движется в однородном магнитном поле с индукцией В=0,2 мТл по винтовой линии. Определить скорость v электрона, если радиус винтовой линии R=3 см, а шаг h=9 см.

426. Ионы двух изотопов с массами m1=6,5×10 –26 кг и m2=6,8×10 –26 кг, ускоренные разностью потенциалов U=0,5 кВ, влетают в однородное магнитное поле с индукцией В=0,5 Тл перпендикулярно линиям индукции. Принимая заряд каждого иона равным элементарному электрическому заряду, определить, насколько будут отличаться радиусы траекторий ионов изотопов в магнитном поле.

427. Частица, несущая один элементарный заряд, влетела в однородное магнитное поле с индукцией В=0,5 Тл. Определить момент импульса L, которым обладала частица при движении в магнитном поле, если её траектория представляла собой окружность радиусом R=0,2 см.

428. Электрон влетает в плоский горизонтальный конденсатор параллельно его пластинам со скоростью u=10 7 м/с. Длина конденсатора l=5 см. Напряжённость электрического поля конденсатора Е=10 кВ/м. При вылете из конденсатора электрон попадает в магнитное поле, перпендикулярное к электрическому полю. Индукция магнитного поля В=10 мТл. Найти радиус R и шаг h винтовой траектории электрона в магнитном поле.

429. Заряженная частица прошла ускоряющую разность потенциалов U=104 В и влетела в скрещенные под прямым углом электрическое (Е=10 кВ/м) и магнитное (В=0,1 Тл) поля. Определить отношение заряда частицы к её массе, если, двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории.

430. Протоны ускоряются в циклотроне в однородном магнитном поле с индукцией В=1,2 Тл. Ускоряющее напряжение 30 кВ. Максимальный радиус кривизны траектории протонов R=40 см. Определить: 1) какое количество оборотов сделает протон до приобретения максимальной кинетической энергии; 2) время ускорения протонов до ЕКмакс.

431. Два бесконечных прямолинейных параллельных проводника с одинаковыми токами, текущими в одном направлении, находятся друг от друга на расстоянии d. Чтобы их раздвинуть до расстояния 2d, на каждый сантиметр длины проводника затрачивается работа А=138 нДж. Определить силу тока в проводниках.

432. Квадратный проводящий контур со стороной l=20 см и током I=10 А свободно подвешен в однородном магнитном поле с индукцией В=0,2 Тл. Определить работу, которую необходимо совершить, чтобы повернуть контур на 180° вокруг оси, перпендикулярной направлению магнитного поля.

433. В однородном магнитном поле с индукцией В=0,2 Тл находится квадратный проводящий контур со стороной l=20 см и током I=10 А. Плоскость контура составляет с направлением поля угол a=30°. Определить работу удаления контура за пределы поля.

434. Круговой проводящий контур радиусом r=5 см и током I=1 А находится в магнитном поле, причём плоскость контура перпендикулярна направлению поля. Напряжённость магнитного поля Н=10 кА/м. Определить работу, которую необходимо совершить, чтобы повернуть контур на 90° вокруг оси, совпадающей с диаметром контура.

435. В однородном магнитном поле с индукцией В=0,5 Тл движется равномерно проводник длиной l=10 см. По проводнику течёт ток I=2 А. Скорость движения проводника u=20 см/с и направлена перпендикулярно к направлению магнитного поля. Определить работу А перемещения проводника за время t=10 с и мощность Р, затраченную на это перемещение.

436. В однородном магнитном поле с индукцией В=1 Тл находится плоская катушка из 100 витков радиусом r=10 см, плоскость которой с направлением поля составляет угол b=60°. По катушке течёт ток I=10 А. Определить работу, которую необходимо совершить, чтобы удалить эту катушку из магнитного поля.

437. По проводу, согнутому в виде квадрата со стороной длиной a=20 см, течет ток I=20 А, сила которого поддерживается неизменной. Плоскость квадрата составляет угол b=20° с линиями индукции однородного магнитного поля (B=0,1Тл). Вычислить работу, которую необходимо совершить для того, чтобы удалить провод за пределы поля.

438. Два прямолинейных длинных параллельных проводника находятся на расстоянии d1=10 см друг от друга. По проводникам в одном направлении текут токи I1=20 А и I2=30 А. Какую работу Al надо совершить (на единицу длины проводников), чтобы раздвинуть эти проводники до расстояния d2 =20 см?

439. По кольцу, сделанного из тонкого гибкого провода радиусом r=10 см, течет ток I=100 А. Перпендикулярно плоскости кольца возбуждено магнитное поле с индукцией В=0,1 Тл, по направлению совпадающей с индукцией В1 собственного магнитного поля кольца. Определить работу внешних сил, которые, действуя на провод, деформировали его и придали ему форму квадрата. Сила тока при этом поддерживалась неизменной. Работой против упругих сил пренебречь.

440. В однородном магнитном поле с индукцией В=0,01 Тл находится прямой провод длиной l=8 см, расположенный перпендикулярно линиям индукции. По проводу течёт ток I=2 А. Под действием сил поля провод переместился на некоторое расстояние S, при этом была совершена работа А=80 мкДж. Определить это расстояние S.

441. В магнитном поле, индукция которого изменяется по закону B=a+bt 2 , где b=10 -2 Тл/с 2 , расположена квадратная рамка со сторо­ной a=20 см, причем плоскость рамки перпендикулярна вектору магнитной индукции. Определить ЭДС индукции в рамке в момент времени t=5 c.

442. Медный диск радиусом a=10 см вращается в однородном магнитном поле, делая 100 оборотов в секунду. Магнитное поле направлено перпендикулярно к плоскости диска и имеет напряжен­ность H=7,96·10 5 А/м. Две щетки, одна на оси диска, другая на окружности, соединяют диск с внешней цепью, в которой включены последовательно резистор с сопротивлением R=10 Ом и амперметр. Что показывает амперметр?

443. Горизонтальный стержень длиной 1 м вращается вокруг вертикальной оси, проходящей через один из его концов. Ось вращения параллельна силовым линиям магнитного поля, индукция которого равна 5·10 –5 Тл. При каком числе оборотов в секунду разность потенциалов на концах этого стержня будет 1 мВ?

444. В однородном магнитном поле, индукция которого равна 0,1 Тл, вращается катушка, состоящая из 200 витков. Ось вращения катушки перпендикулярна ее оси и направлению магнитного поля. Период вращения катушки равен 0,2 с, площадь поперечного сечения катушки 4 см 2 . Найти максимальную ЭДС индукции во вращаю­щейся катушке.

445. В однородном магнитном поле, индукция которого 0,8 Тл, равномерно вращается рамка с угловой скоростью 15 рад/с. Площадь рамки 150 см 2 . Ось вращения находится в плоскости рамки и состав­ляет 30 ° с направлением силовых линий магнитного поля. Найти максимальную ЭДС индукции во вращающейся рамке.

446. Скорость самолёта с реактивным двигателем равна 950 км/ч. Найти ЭДС индукции, возникающую на концах крыльев самолёта, если вертикальная составляющая напряжённости магнитного поля земли 39,8 А/м и размах крыльев самолёта 12,5 м.

447. В однородном магнитном поле с индукцией 1 Тл равномерно вращается рамка, содержащая 1000 витков провода. Площадь рамки 150 см 2 . Рамка вращается с частотой 10 об/с. Определить мгновен­ное значение ЭДС, соответствующее углу поворота рамки 30°. Ось вращения перпендикулярна линиям индукции и лежит в плоскости рамки.

448. Проволочный виток радиусом 4 см и сопротивлением 0,01 Ом находится в однородном магнитном поле с напряжённостью 5000 А/м. Плоскость рамки составляет 30° с линиями напряжённости. Какое количество электричества протечёт по витку, если магнитное поле выключить?

449. Проволочное кольцо радиусом R=10 см лежит на столе. Какое количество электричества q протечёт по кольцу, если его перевернуть с одной стороны на другую? Сопротивление кольца r=1 Ом. Вертикальная составляющая индукции магнитного поля земли В=50 мкТл.

450. Для измерения индукции магнитного поля между полюсами магнита помещена катушка, состоящая из 50 витков проволоки и соединённая с баллистическим гальванометром. Ось катушки параллельна направлению магнитного поля. Площадь поперечного сечения катушки 2 см 2 , сопротивлением её по сравнению с сопротивлением гальванометра можно пренебречь. Сопротивление гальванометра 2×10 3 Ом, его баллистическая постоянная 2×10 -8 Кл/дел. При быстром выдёргивании катушки из магнитного поля гальванометр даёт отброс, равный 50 делениям шкалы. Чему равна индукция магнитного поля?

451. В магнитном поле, индукция которого равна 0,05 Тл, поме­щена катушка, содержащая 200 витков проволоки. Сопротивление катушки 40 Ом, площадь её поперечного сечения 12 см 2 . Катушка помещена так, что её ось составляет 60 o с направлением магнитного поля. Какое количество электричества протечёт по катушке при исчезновении поля?

452. В однородном магнитном поле, индукция которого 1 Тл, находится прямой проводник длиной 20 см. Концы проводника замкнуты проводом, находящимся вне поля. Сопротивление всей цепи 0,1 Ом. Найти силу, которую надо приложить к проводнику, чтобы перемещать его со скоростью 2,5 м/с перпендикулярно линиям индукции.

453. Электрическая лампочка, сопротивление которой в горячем состоянии равно 10 Ом, подключается через дроссель к двенадцати­вольтовому аккумулятору. Индуктивность дросселя 2 Гн, сопротив­ление 1 Ом. Через сколько времени после включения лампочка загорится, если она начинает светиться при напряжении на ней 6 В?

454. Имеется катушка длиной 20 см и диаметром 2 см. Обмотка катушки состоит из 200 витков медной проволоки, площадь попе­речного сечения которой 1 мм 2 . Катушка включена в цепь с некоторой ЭДС. При помощи переключателя ЭДС выключается и катушка замыкается накоротко. Через сколько времени после выключения ЭДС сила тока в цепи уменьшается в 2 раза?

455. Рамка площадью S=100 см 2 содержит N=1000 витков провода с сопротивлением r1=12 Ом. К концам обмотки подключено внешнее сопротивление r2=20 Ом. Рамка равномерно вращается в магнитном поле (B=0,1 Тл), делая n=2 об/с. Чему равно максимальное значение мощности переменного тока во внешней цепи? Ось вращения, лежащая в плоскости рамки, перпендикулярна линиям индукции.

456. Квадратная рамка из медной проволоки сечением 1 мм 2 помещена в магнитное поле, индукция которого меняется по закону B=B0sinwt, где B0=0,01 Тл, w=2p/T и T=0,02 c. Площадь рамки 25 см 2 . Плоскость рамки перпендикулярна к направлению магнитного поля. Найти максимальную силу тока, возникающую в рамке.

457. В соленоид длиной 50 см вставлен ферромагнитный сердечник. Число витков на единицу длины соленоида равно 400 вит./м. Найти индуктивность соленоида, если при силе тока 2 А по обмотке соленоида магнитный поток, пронизывающий поперечное сечение соленоида, равен 1,6 мВб.

458. Обмотка соленоида состоит из одного слоя плотно прилегаю­щих друг к другу витков медного провода. Диаметр провода 0,2 мм, диаметр соленоида 5 см. По соленоиду течёт ток силой 1 А. Опреде­лить, какое количество электричества протечёт через обмотку, если концы её замкнуть накоротко.

459. Тонкий медный проводник массой m=1 г согнут в виде квад­рата и концы его замкнуты. Квадрат помещён в однородное магнит­ное поле (B=0,1 Тл) так, что плоскость его перпендикулярна линиям индукции поля. Определить количество электричества q, которое протечёт по проводнику, если квадрат, потянув за противополож­ные вершины, вытянуть в линию.

460. Обмотка соленоида состоит из N витков медной проволоки, поперечное сечение которой 1 мм 2 . Длина соленоида 25 см и сопротивление его обмотки 0,2 Ом. Найти индуктивность соленоида. Удельное сопротивление меди 1,7×10 –8 Ом×м.

461. На соленоид, длина которого равна 21 см и площадь попереч­ного сечения 10 см 2 , надета катушка, состоящая из 50 витков. Катушка соединена с баллистическим гальванометром, сопротивле­ние которого 10 3 Ом. По обмотке соленоида, состоящей из 200 витков, идёт ток силой 5 А. Какой заряд пройдёт по гальванометру, если ток соленоида станет равным нулю?

462. На соленоид длиной 144 см и диаметром 5 см надет проволоч­ный виток. Обмотка соленоида имеет 2000 витков и по ней течёт ток в 2 А. Соленоид содержит железный сердечник. Какая средняя ЭДС индуцируется в надетом на соленоид витке, когда ток в соленоиде выключается в течение 0,002 с?

463. Обмотка тороида имеет N1=251 виток. Средний диаметр тороида 8 см, диаметр витков 2 см. На тороид намотана вторичная обмотка N2, имеющая 100 витков. При замыкании первичной обмотки в ней в течение 0,001 с устанавливается ток силой 3 А. Найти среднее значение ЭДС индукции во вторичной обмотке.

464. На соленоид длиной 20 см и площадью поперечного сечения 30 см 2 надет проволочный виток. Соленоид имеет 320 витков и по нему течёт ток в 3 А. Какая средняя ЭДС индуцируется в надетом на соленоид витке, когда ток в соленоиде выключается в течение 0,001 с?

465. Две катушки имеют взаимную индуктивность, равную 0,005 Гн. В первой катушке сила тока изменяется по закону I=I0 sin wt, где I0=10 А, w=2p/T, T=0,02 с. Найти наибольшее значение ЭДС индук­ции во второй катушке.

466. Вычислить взаимную индуктивность длинного прямого провода и прямоугольной рамки со сторонами a и b. Рамка и провод лежат в одной плоскости, причём ближайшая сторона рамки длиной a параллельна проводу и отстоит от него на расстоянии l.

467. Два концентрических тонких проводника в форме окружно­стей с радиусами a и b лежат в одной плоскости (a –8 Кл?

470. Определить взаимную индуктивность L12 тороида и проходя­щего по его оси бесконечного прямого провода. Тороид имеет прямоугольное сечение ширины a. Внутренний радиус тороида r1, внешний r2. Число витков тороида N. Тороид и провод погружены в среду с проницаемостью m.

471. Длинный цилиндр радиусом R, заряженный равномерно по поверхности, вращается вокруг своей оси с угловой скоростью w. Найти энергию магнитного поля на единицу длины цилиндра, если линейная плотность заряда цилиндра равна l, а m=1.

472. При некоторой силе тока плотность энергии магнитного поля соленоида (без сердечника) w=0,2 Дж/м 3 . Во сколько раз увеличится плотность энергии этого поля при той же силе тока, если соленоид будет иметь железный сердечник?

473. Соленоид содержит N=1000 витков. Сила тока в обмотке I=1 А, магнитный поток через поперечное сечение соленоида Фm=0,01 Вб. Вычислить энергию магнитного поля.

474. Обмотка тороида содержит 10 витков на каждый сантиметр длины. Сердечник немагнитный. При какой силе тока плотность энергии магнитного поля равна 1 Дж/м 3 .

475. На стержень из немагнитного материала длиной l=50 см и сечением S=2 см 2 намотан в один слой провод так, что на каждый сантиметр длины стержня приходится 20 витков. Определить энергию W магнитного поля внутри соленоида, если сила тока в обмотке I=0,5 А.

476. На железное кольцо намотано в один слой N=200 витков. Чему равна энергия магнитного поля, если при токе I=2,5 А магнитный поток в железе 0,5 мВб?

477. По обмотке тороида течёт ток I=0,6 А. Витки провода диамет­ром d=0,4 мм плотно прилегают друг к другу. Найти энергию магнитного поля в стальном сердечнике тороида, если площадь поперечного сечения его S=4 см 2 , диаметр средней линии D=30 см.

478. Индукция магнитного поля тороида со стальным сердечником возросла от B1=0,5 Тл до B2=1 Тл. Найти, во сколько раз изменилась объёмная плотность энергии магнитного поля.

479. Катушка индуктивностью L=2 мкГн и сопротивлением R0=1 Ом подключена к источнику постоянного тока с ЭДС e=3 В. Парал­лельно катушке включено сопротивление R=2 Ом. После того как ток в катушке достигнет установившегося значения, источник тока отключается. Найти количество тепла, выделивше­еся на сопротивлении R после отключения источника. Сопротивле­нием источника и соединительных проводов пренебречь.

480. Железный сердечник, имеющий форму тора с квадратным се­чением, несёт на себе обмотку из N=1000 витков. Внутренний радиус тора a=0,2 м, внешний b=0,25 м. Определить энергию, запасённую в сердечнике в том случае, если по обмотке течёт ток I=1,26 А. Определение произвести приближённо, полагая напряжён­ность поля по всему сечению тороида одинаковой и равной значе­нию H в центре сечения.

Варианты контрольного задания № 4

№ вариантаНомера задач контрольного задания

Библиографический список

1. Савельев, И. В. Курс общей физики: в 3 т. Т.2. Электричество и магнетизм. Волны. Оптика: учеб. пособие для втузов /И.В. Савельев. 3-е изд., испр. М., 1987. 496 с.

2. Трофимова, Т. И. Курс физики: учеб. пособие для инж.–техн. специальностей вузов /Т.И. Трофимова. 4 -е изд., испр. М.: Высш. школа, 1997. 542 с.

3. Курс физики: учебник для вузов: в 2 т. /Под ред. В. Н. Лозовского. 2-е изд., испр. СПб.: Лань, 2001. Т. 1. 576 с.

3. Детлаф, А. А., Яворский Б. М. Курс физики: учеб. пособие для втузов / А. А. Детлаф, Б. М. Яворский. 1989. 608 с.

4. Яворский, Б. М., Справочник по физике / Б.М. Яворский, А.А. Детлаф. 2-е изд., перераб. М.: Наука, 1985. 512 с.

5. Чертов, А. Г. Задачник по физике /А.Г. Чертов, А.А. Воробьёв. 5-е изд., перераб. и доп. М., 1988. 526 с.

6. Волькенштейн, В. С. Сборник задач по общему курсу физики: [для втузов] /В.С. Волькенштейн. 11-е изд. перераб. М.: Наука, 1985. 381 с.

7. Беликов, Б. С. Решение задач по физике. Общие методы: учеб. пособие для вузов / Б.С. Беликов. М.: Высш. школа, 1986. 255 с.

Уравнения максвелла примеры решения задач

Удельное сопротивление проводников (при 0 0 С), мкОмּм

Алюминий0,025Нихром
Графит0,039Ртуть0,94
Железо0,087Свинец0,22
Медь0,017Сталь0,10

Содержание

Содержание теоретического курса . . . . . . 3

1. Электростатика и постоянный ток . . . . . 5

1.1. Электрический заряд. Закон сохранения заряда.

Закон Кулона. Напряженность поля . . . . . 5

1.2. Принцип суперпозиции полей . . . . . . 7

1.3. Поток напряженности. Теорема Гаусса

для электростатического поля в вакууме . . . . 8

1.4. Потенциал электростатического поля.

Работа совершаемая силами электростатического поля

при перемещении в нем электрического заряда . . . 9

1.5. Примеры применения теоремы Гаусса к расчету

электростатических полей . . . . . . 10

1.6. Электрическое поле в диэлектрической среде.

Дипольные моменты молекул диэлектрика.

Поляризация диэлектрика . . . . . . 12

1.7. Теорема Гаусса для электростатического поля в среде . . 13

1.8. Условия для электростатического поля на границе раздела

изотропных диэлектрических сред . . . . . 14

1.9. Проводники в электростатическом поле.

Электроемкость проводника . . . . . . 14

1.10. Взаимная емкость. Конденсаторы . . . . . 15

1.11. Потенциальная энергия системы точечных зарядов.

Энергия заряженного проводника и электрического поля . 16

1.12. Постоянный электрический ток. Сила и плотность тока . 16

1.13. Законы постоянного тока. Сторонние силы . . . 18

1.14. Правила Кирхгофа . . . . . . . 19

Примеры решения задач . . . . . . 20

Задачи для самоконтроля . . . . . . 28

Контрольное задание №3 . . . . . . 30

2. Магнетизм . . . . . . . . . 38

2.1. Сила Лорентца и сила Ампера. Вектор магнитной индукции . 38

2.2. Закон Био и Савара. Принцип суперпозиции.

Магнитные поля прямого и кругового токов . . . 40

2.3. Магнитное взаимодействие проводников с токами.

Контур с током в магнитном поле . . . . . 41

2.4. Циркуляция магнитного поля (закон полного тока) в вакууме.

Теорема Гаусса для магнитного поля . . . . . 42

2.5. Работа перемещения проводника с током в магнитном поле . 43

2.6. Движение заряженных частиц в магнитном

и электрическом полях . . . . . . . 44

2.7. Магнитные моменты электронов и атомов.

Видео:О чем говорят уравнения Максвелла? Видео 1/2Скачать

О чем говорят уравнения Максвелла? Видео 1/2

Решение уравнений Максвелла; потенциалы и волновое уравнение

Теперь стоило бы заняться немного математикой; мы запишем уравнения Максвелла в более простой форме. Вы, пожалуй, сочтете, что мы усложняем их, но если вы наберетесь терпения, то внезапно обнаружите их большую простоту. Хотя вы уже вполне привыкли к каждому из уравнений Максвелла, имеется все же много частей, которые стоит соединить воедино. Вот как раз этим мы и займемся.

Начнем с V·В=0 — простейшего из уравнений. Мы знаем, что оно подразумевает, что В — есть ротор чего-то. Поэтому, если вы записали

Уравнения максвелла примеры решения задач

то считайте, что уже решили одно из уравнений Максвелла. (Между прочим, заметьте, что оно остается верно для другого вектора А′, если A′=A+ vψ), где ψ — любое скалярное поле, потому что ротор vψ — нуль и В — по-прежнему то же самое. Мы говорили об этом раньше.)

Теперь разберем закон Фарадея VxE= –∂B/∂t, потому что он не содержит никаких токов или зарядов. Если мы запишем В как V X А и продифференцируем по t, то сможем переписать закон Фарадея в форме

Уравнения максвелла примеры решения задач

Поскольку мы можем дифференцировать сначала либо по времени, либо по координатам, то можно написать это уравнение также в виде

Уравнения максвелла примеры решения задач

Мы видим, что E+∂A/∂t — это вектор, ротор которого ранен нулю. Поэтому такой вектор есть градиент чего-то. Когда мы занимались электростатикой, у нас было VxE=0, и мы тогда решили, что Е — само градиент чего-то. Пусть это градиент от –φ (минус для технических удобств). То же самое сделаем и для E+∂A/∂t; мы полагаем

Уравнения максвелла примеры решения задач

Мы используем то же обозначение φ, так что в электростатическом случае, когда ничто не меняется со временем и ∂A/∂t исчезает, Е будет нашим старым –vφ. Итак, закон Фарадея можно представить в форме

Уравнения максвелла примеры решения задач

Мы уже решили два из уравнений Максвелла и нашли, что для описания электромагнитных полей Е и В нужны четыре потенциальные функции: скалярный потенциал φ и векторный потенциал А, который, разумеется, представляет три функции.

Итак, А определяет часть Е, так же как и В. Что же произойдет, когда мы заменим А на A′=A+vψ? В общем, Е должно было бы измениться, если не принять особых мер. Мы можем, однако, допустить, что А изменяется так, чтобы не влиять на поля Е и В (т. е. не меняя физики), если будем всегда изменять А и φ вместе по правилам

Уравнения максвелла примеры решения задач

Тогда ни В, ни Е, полученные из уравнения (18.19), не меняются.

Раньше мы выбирали V ·А=0, чтобы как-то упростить уравнения статики. Теперь мы не собираемся так поступать; мы хотим сделать другой выбор. Но подождите немного, прежде чем мы скажем, какой это выбор, потому что позднее станет ясно, почему вообще делается выбор.

Сейчас мы вернемся к двум оставшимся уравнениям Максвелла, которые свяжут потенциалы и источники ρ и j. Раз мы можем определить А и φ из токов и зарядов, то можно всегда получить Е и В из уравнений (18.16) и (18.19) и мы будем иметь другую форму уравнений Максвелла.

Начнем с подстановки уравнения (18.19) в v·E=ρ/ε0; получаем

Уравнения максвелла примеры решения задач

это можно записать еще в виде

Уравнения максвелла примеры решения задач

Таково первое уравнение, связывающее φ и А с источниками.

Наше последнее уравнение будет самым трудным. Мы начнем с того, что перепишем четвертое уравнение Максвелла:

Уравнения максвелла примеры решения задач

а затем выразим В и Е через потенциалы, используя уравнения (18.16) и (18.19):

Уравнения максвелла примеры решения задач

Первый член можно переписать, используя алгебраическое тождество v x (vxA) = V (V·A) – v 2 A; мы получаем

Уравнения максвелла примеры решения задач

Не очень-то оно простое!

К счастью, теперь мы можем использовать нашу свободу в произвольном выборе дивергенции А. Сейчас мы собираемся сделать такой выбор, чтобы уравнения для А и для φ разделились, но имели одну и ту же форму. Мы можем сделать это, выбирая ,

Уравнения максвелла примеры решения задач

Когда мы поступаем так, то второе и третье слагаемые в уравнении (18.22) погашаются, и оно становится много проще:

Уравнения максвелла примеры решения задач

И наше уравнение (18.21) для φ принимает такую же форму:

Уравнения максвелла примеры решения задач

Какие красивые уравнения! Они великолепны прежде всего потому, что хорошо разделились — с плотностью заряда стоит φ, а с током стоит А. Далее, хотя левая сторона выглядит немного нелепо — лапласиан вместе с (∂/∂t) 2 , когда мы раскроем ее, то обнаружим

Уравнения максвелла примеры решения задач

Это уравнение имеет приятную симметрию по х, у, z, t; здесь (–1/с 2 ) нужно, конечно, потому, что время и координаты различаются; у них разные единицы.

Уравнения Максвелла привели нас к нового типа уравнению для потенциалов φ и А, но с одной и той же математической формой для всех четырех функций φ, Ах, Ау и Az. Раз мы научились решать эти уравнения, то можем получить В и Е из vXE и —vφ —∂A/∂t. Мы приходим к другой форме электромагнитных законов, в точности эквивалентной уравнениям Максвелла; с ними во многих случаях обращаться гораздо проще.
Фактически мы уже решали уравнение, весьма похожее на (18.26). Когда мы изучали звук в гл. 47 (вып. 4), мы имели уравнение в форме

Уравнения максвелла примеры решения задач

и видели, что оно описывает распространение волн в x-направлении со скоростью с. Уравнение (18.26) это соответствующее волновое уравнение для трех измерений. Поэтому в области, где больше нет зарядов и токов, решение этих уравнений не означает, что φ и А — нули. (Хотя на самом деле нулевое решение есть одно из возможных решений.) Имеются решения, представляющие некоторую совокупность φ и А, которые меняются со временем, но всегда движутся со скоростью с. Поля передвигаются вперед через свободное пространство, как в нашем примере в начале главы.

С новым членом, добавленным Максвеллом в уравнение IV, мы смогли записать полевые уравнения в терминах А и φ в форме, которая проста и сразу же позволяет выявить существование электромагнитных волн. Для многих практических целей еще будет удобно использовать первоначальные уравнения в терминах E и В. Но они — по ту сторону горы, на которую мы уже вскарабкались. Теперь мы можем посмотреть вокруг. Все будет выглядеть иначе — нас ожидают новые, прекрасные пейзажи.

📹 Видео

3 14 Уравнения МаксвеллаСкачать

3 14 Уравнения Максвелла

ЧК_МИФ /ЛИКБЕЗ/ 3_3_5_1 СИСТЕМА УРАВНЕНИЙ МАКСВЕЛЛА. ПРИМЕРЫ (минимум теории)Скачать

ЧК_МИФ /ЛИКБЕЗ/ 3_3_5_1 СИСТЕМА УРАВНЕНИЙ МАКСВЕЛЛА. ПРИМЕРЫ (минимум теории)

ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать

ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений Максвелла

Уравнения Максвелла 2021Скачать

Уравнения Максвелла 2021

Как решают уравнения в России и США!?Скачать

Как решают уравнения в России и США!?

Как распознать талантливого математикаСкачать

Как распознать талантливого математика

Дельта альфа альфа штрих | МФТИСкачать

Дельта альфа альфа штрих | МФТИ

6.1 Решение уравнений Максвелла с заданным сторонним электрическим током методом ЭД потенциаловСкачать

6.1 Решение уравнений Максвелла с заданным сторонним электрическим током методом ЭД потенциалов

7. Ограниченность уравнений Максвелла. Уточнения уравнений электродинамики. Ацюковский В.А.Скачать

7. Ограниченность уравнений Максвелла. Уточнения уравнений электродинамики. Ацюковский В.А.

Уравнение, которое меняет взгляд на мир [Veritasium]Скачать

Уравнение, которое меняет взгляд на мир [Veritasium]

Урок 272. Задачи на закон Ампера - 1Скачать

Урок 272. Задачи на закон Ампера - 1

Решение уравнения Максвелла 2D для z-компоненты магнитного поляСкачать

Решение уравнения Максвелла 2D для z-компоненты магнитного поля

Как решить уравнение #россия #сша #америка #уравненияСкачать

Как решить уравнение #россия #сша #америка #уравнения

Билет №34 "Электромагнитные волны"Скачать

Билет №34 "Электромагнитные волны"

Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Урок 4. Расчет цепей постоянного тока. Законы Кирхгофа

Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать

Урок 147. Задачи на основное уравнение МКТ идеального газа
Поделиться или сохранить к себе:
О сайте | | © 2024 Про уравнения - легко.