Уравнения линий в полярной системе координат задающих окружности (2 видео)

Уравнения линий в полярных координатах

По существу, уравнение линии в полярной системе координат представляет собой функцию полярного радиуса от полярного угла (аргумента). При этом полярный угол учитывается в радианах и непрерывно принимает значения от 0 до (иногда следует рассмотреть до бесконечности, или же в ряде задач для удобства от до ). Каждому значению угла «фи», которое входит в область определения функции , соответствует единственное значение полярного радиуса.

Примером полярной кривой является Архимедова спираль . На следующем рисунке изображен её первый виток — когда полярный радиус вслед за полярным углом принимает значения от 0 до :

Одна из ветвей спирали Архимеда, задаваемая уравнением для .Архимедова спираль названа в честь её изобретателя, древнегреческого математика Архимеда. Эту спираль можно определить с помощью простого полярного уравнения:

Изменения параметра приводят к повороту спирали, а параметра — расстояния между витками, которое является константой для конкретной спирали. Спираль Архимеда имеет две ветви, одну для а другую для . Две ветви плавно соединяются в полюсе. Зеркальное отображение одной ветви относительно прямой, проходящей через угол 90°/270°, даст другую ветвь. Эта кривая интересна тем, что была описана в математической литературе одной из первых, после конического сечения, и лучше других определяется именно полярным уравнением.

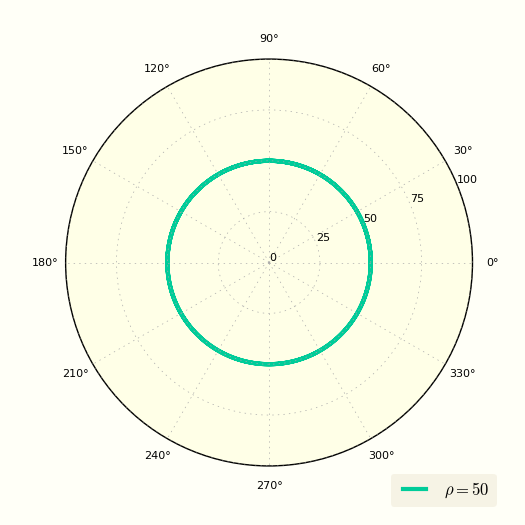
Круг, заданный уравнением .

Общее уравнение окружности с центром в () и радиусом имеет вид:

Это уравнение может быть упрощено для частных случаев, например является уравнением, определяющим окружность с центром в полюсе и радиусом . [14]

Радиальные прямые (те, которые проходят через полюс) определяются уравнением где — угол, на который прямая отклоняется от полярной оси, то есть, где — наклон прямой в прямоугольной системе координат. Нерадиальная прямая, перпендикулярно пересекает радиальную прямую в точке определяется уравнением

Полярная роза задана уравнением

Полярная роза — известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах: для произвольной постоянной (включая 0). Если — целое число, то это уравнение будет определять розу с лепестками для нечётных , либо с лепестками для чётных . Если — рациональное, но не целое, график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут перекрываться. Если — иррациональное, то роза состоит из бесконечного множества частично накладывающихся друг на друга лепестков. Розы с 2, 6, 10, 14 и т. д. лепестками этим уравнением определить невозможно. Переменная определяет длину лепестков.

Если считать, что радиус не может быть отрицательным, то при любом натуральном мы будем иметь -лепестковую розу. Таким образом, уравнение будет определять розу с двумя лепестками. С геометрической точки зрения радиус — это расстояние от полюса до точки и он не может быть отрицательным.

— является частным случаем полярной розы.

Трехлепестковая роза задается уравнением

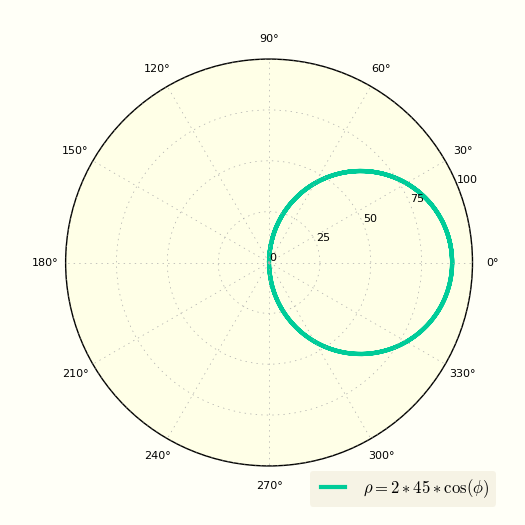
Коническое сечение, один из полюсов которого находится в полюсе, а другой где-то на полярной оси (так, что малая полуось лежит вдоль полярной оси) задаётся уравнением:

где — эксцентриситет, а — фокальный параметр. Если , это уравнение определяет гиперболу; если , то параболу; если , то эллипс. Отдельным случаем является , определяющее окружность с радиусом .

Лемнискамта (от лат. lemniscatus — «украшенный лентами») — плоская алгебраическая кривая порядка , у которой произведение расстояний от каждой точки до заданных точек (фокусов) постоянно и равно квадрату половины расстояния между фокусами.

Рассмотрим простейший случай: если расстояние между фокусами равняется , расположены они на оси , и начало координат делит отрезок между ними пополам, то следующие уравнения задают лемнискату:

· в прямоугольных координатах:

Проведя несложные преобразования, можно получить явное уравнение:

· в полярных координатах:

-плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности с таким же радиусом [1] . Получила своё название из-за схожести своих очертаний со стилизованным изображением сердца.

Кардиоида является частным случаем улитки Паскаля, эпициклоиды и синусоидальной спирали.

Пусть — радиус окружностей, начало координат находится в крайней правой точке горизонтального диаметра неподвижной окружности. Тогда уравнения кардиоиды можно записать в следующих формах:

В прямоугольных координатах:

В прямоугольных координатах (параметрическая запись):

В полярных координатах [2][1] :

(от греч. буфспн — звезда и ейдпт — вид, то есть звездообразная) [1] — плоская кривая, описываемая точкой окружности радиуса r, катящейся по внутренней стороне окружности радиуса . Иначе говоря, астроида — это гипоциклоида с модулем k =4.

Уравнение в декартовых прямоугольных координатах:

Астроида также является алгебраической кривой рода 1 (и шестого порядка). Уравнение в алгебраическом виде:

Пример 2.3.Составить уравнение прямой линии в полярных координатах.

Поместим полюс полярной системы координат в начало прямоугольной системы координат, полярную ось совместим с положительной полуосью абсцисс (см. рис. 17).

Возьмем уравнение прямой в нормальном виде

Формулы перехода имеют вид

Подставив в это уравнение значения x и y из формулы (2.1), получим ,или, откуда , и окончательно .

В этом уравнении постоянными величинами являются p и , величины же r и — переменные: это текущие полярные координаты точки на прямой (последняя формула может быть получена также из чертежа).

Пример 2.4. Построить кривую r = a cos 2ц и найти ее уравнение в прямоугольной системе координат.

Будем давать значения полярному углу от до через промежуток и вычислим соответствующие значения r. Найденные значения поместим в таблицу. Примем произвольный отрезок за единицу масштаба, которой будем пользоваться при построении r. По значениямr и из таблицы построим точки, соответствующие каждой паре чисел r и , и соединим их плавной кривой.

Уравнения линий в полярной системе координат задающих окружности

0
— a
0

Построение кривой показано на следующих рисунках:

На рисунке кривые, построенные на различных этапах, соединены в одну. Полученная кривая называется четырехлепестковой розой.

Теперь найдем уравнение четырехлепесковой розы в прямоугольной системе координат, причем напоминаем, что начало прямоугольной системы координат помещено в полюс полярной системы координат, а ось абсцисс направлена вдоль полярной оси.

Учитывая, что , уравнение четырехлепестковой розы перепишем в виде . Подставляя сюда формулы перехода

Возводя обе части последнего уравнения в квадрат, получим окончательно

Пример 2.5. Линия задана уравнением в полярной системе координат.

1) построить линию по точкам начиная с до и придавая значения через промежуток ;

2) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс — с полярной осью;
3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия.

Построим линию по точкам, предварительно заполнив таблицу значений r и :

Используя данные таблицы, строим линию:

Найдем уравнение данной линии в декартовой системе координат:

Содержание

Уравнение окружности в полярной системе координат.
Окружность в полярных координатах
Построение окружности по простому уравнению в полярной системе координат
Еще одно уравнение окружности в полярных координатах
Уравнение окружности в полярных координатах
Построение окружности в полярной системе координат
Теперь сместим окружность по вверх, очередное уравнение окружности в полярных координатах
📹 Видео

Видео:Полярная система координатСкачать

Уравнение окружности в полярной системе координат.

Определим уравнение окружности, проходящей через полюс системы координат, центр которой C расположен на полярной оси, а радиус равен R. Выполним построения:

Далее отметим на окружности любую точку А и В, причем точка В — конец диаметра. Соединим выбранную пару точек. Угол ОАВ — прямой, а потому, так как диаметр равен 2R, из прямоугольного треугольника АОВ имеем:

Если же центр является началом координат, то уравнение принимает вид: