Уравнения линий ликвидуса и солидуса (8 видео)

Лекция 12-13. Двойные диаграммы состояния

Двойные диаграммы состояния

О составе фаз, образующихся в двухкомпонентной системе, о температурах, при которых эти фазы образуются и существуют можно судить из данных термического анализа.

Термин «состав» может иметь три значения:

1) состав отдельной фазы;

2) относительные количества различных фаз, входящих в смесь, т. е. фазовый состав;

3) общий состав смеси по компонентам без учета присутствующих фаз, т. е. компонентный состав.

Кривая ликвидуса xyz определяет зависимость наивысшей температуры, при которой еще могут существовать кристаллы, от состава системы (рисунок 1). Точки, соответствующие жидкостям, состав которых лежит между А и е, при охлаждении пересекают ликвидус на участке х—у и попадают в двухфазную область «А + жидкость». Для этих составов А ‑ первичная фаза, поскольку при охлаждении в первую очередь кристаллизуется эта фаза. Линия cyd называется линией солидуса; она определяет минимальную температуру равновесного существования жидкости в охватываемом ею интервале составов. Точка у является точкой нонвариантного сосуществования трех фаз: А, В и жидкости. Эта точка носит название эвтектики, она соответствует минимальной температуре, при которой система (в данном случае состава е) может целиком находиться в жидкой фазе. Кроме того, температура эвтектики есть самая низкая для всей системы температура существования жидкости.

Рисунок 1 – Диаграмма системы простого эвтектического типа

Рассмотрим состав f. Ниже Т1 он состоит из смеси фаз А и В, а выше Г4 становится полностью жидким. В интервале Т1-Т4 сосуществуют жидкость и кристаллическая фаза В, относительные количества которых меняются с температурой и могут быть определены по правилу рычага. Относительные количества сосуществующих фаз обратно пропорциональны расстояниям по оси составов от составов этих фаз до суммарного состава системы. Так, при Т2 жидкость имеет состав h`; ее доля в смеси определяется соотношением fВ: Bh, а доля фазы В ‑ отношением fh: Вh. Правило рычага аналогично правилу моментов в механике, но вместо веса грузов (подвешенных к палочке на разных расстояниях от оси) здесь выступают различные количества двух фаз, образующих общий заданный или компонентный состав. Правило рычага можно вывести на основании правила моментов следующим образом. Состав f при температуре Т2 представлен двумя равновесными фазами ‑ В и жидкостью h‘. Их относительные количества определяются условием:

(доля жидкости h`).(расстояние hf) = (доля твердой фазы В).(расстояние Bf)

Доля жидкости h` =

Пользуясь правилом рычага, можно определить изменения относительного состава смеси (количества отдельных фаз) с температурой. Так, при температуре Т2 для состава f доля жидкости равна отношению Вf:Bh (≈ 0,38). При более высокой температуре Т3 она равна Вf:Вe (≈ 0,5), а при более низкой температуре, лишь немного превышающей температуру солидуса Т1, доля жидкости определяется отношением Вf: Be ( ≈ 0,33). При Т4 вся смесь представляет собой расплав, т. е. доля жидкости равна 1, что означает завершение плавления. Поскольку доля расплава с повышением температуры возрастает, то соответствующим образом должен меняться состав жидкой фазы: она обогащается компонентом В, поскольку кристаллы фазы В постепенно растворяются в жидкой фазе. Первые порции жидкости, возникающие при Т1, содержат

33 % В и 67 % А (состав е). При продолжении плавления состав жидкости следует по кривой ликвидуса yh‘j‘g до полного плавления при T4. Здесь, в точке f, жидкость имеет состав

78 % В и 22 % А. При охлаждении жидкости в равновесных условиях должен происходить обратный процесс: при T4 начинается образование кристаллов В из жидкости f, и чем ниже температура, тем дальше сдвигается состав жидкости от точки g к точке у в результате выпадения все большего количества кристаллов В.

Рассмотрим так называемую эвтектическую реакцию, которая происходит в тот момент, когда в результате охлаждения температура достигает значения Т1 Применим к этому случаю правило рычага. Чуть выше Т1 доля фазы В определяется отношением fе:Ве ≈ 0,67, а чуть ниже этой температуры доля фазы В равна fА:ВА ≈ 0,78. Таким образом, оставшаяся жидкость состава е кристаллизуется в виде смеси фаз А и В, причем кристаллы А образуются впервые, а количество кристаллов В при этом просто увеличивается.

Смесь твердых компонентов А и В, имеющая суммарный состав е при Т1 претерпевает полное плавление, и, наоборот, гомогенная жидкость этого состава при Т1 полностью кристаллизуется в виде смеси фаз А и В.

Предложенное выше описание эвтектической реакции соответствует равновесным условиям, что требует чрезвычайно медленных скоростей нагревания и в особенности охлаждения. Охлаждение с высокими скоростями часто (особенно в системах с более сложными диаграммами состояния) приводит к другим результатам.

Кривую ликвидуса xyz можно рассматривать в различных аспектах: с одной стороны, это линия максимальных температур существования кристаллических фаз, а с другой ‑ кривая предельной растворимости компонентов в расплаве. Так, участок ликвидуса yz определяет предельную растворимость В в расплаве и ее изменение с температурой. Выше этой кривой существует гомогенный раствор (расплав), а ниже присутствуют также нерастворившиеся кристаллы В. При охлаждении ниже кривой yz эти кристаллы должны выпадать, хотя в некоторых ситуациях образуются метастабильные (переохлажденные) пересыщенные растворы.

Кривая ликвидуса показывает влияние растворения примесей на температуру плавления чистых компонентов. Например, если к В при температуре Т4 добавить небольшое количество А, то появится некоторое количество жидкости состава g. При увеличении количества добавляемого компонента А количество жидкости g будет возрастать до тех пор, пока состав всей системы не достигнет точки g, в которой твердая фаза исчезает полностью, а образец становится полностью жидким. Следовательно, небольшое количество растворимой примеси А понизило температуру плавления В от Т5 до Т4. Этот эффект находит знакомое всем практическое применение при очистке дорог от обледенения путем посыпания солью. В бинарной системе Н2О— NaCl имеется эвтектика при -21 °С, вследствие чего при добавлении NaCl температура плавления льда становится ниже 0°С.

На основании кривых нагревания и охлаждения исследуемых образцов строят Т-Х ‑ диаграмму состояния изучаемой системы. Состав системы выражают в весовых или мольных процентах, мольных или атомных долях. Если производится исследование систем, состояние равновесия в которых практически зависит от давления, то такие системы называются конденсированными.

На рисунке 2 приведены кривые охлаждения чистого компонента и сплавов, содержащих различные смеси первого и второго компонентов.

Рисунок 2 ‑ Кривые охлаждения чистых компонентов и сплавов

В случае одного компонента на кривой охлаждения имеется горизонтальная площадка при температуре плавления компонента, что соответствует безвариантному равновесия двух фаз: жидкость + твердая фаза. Правило фаз для конденсированной системы записывают в виде:

(n — число компонентов, K — число фаз, F — число степеней свободы).

При К = 2 в однокомпонентной конденсированной системе (n = 1) F = 0, поэтому процесс плавления происходит при постоянной температуре. В случае двухкомпонентной системы правило фаз записывается в виде:

На рисунке 2 на кривых охлаждения смесей двух компонентов 1, 2, 3,4 излом в точках a, b, c, d соответствует началу кристаллизации одного из компонентов. В этот момент число степеней свободы равно единице (F = 2 + 1 — 2); т. е. система является моновариантной, поэтому во время кристаллизации температура продолжает изменяться, но с другой стороны, так как выделяющаяся теплота кристаллизации замедляет падение температуры. На кривой охлаждения появляется излом, затем начинается кристаллизация второго компонента, так как при этом число фаз становится равным 3, то число степеней свободы равно нулю. Процесс кристаллизации второго компонента происходит при постоянной температуре, и на кривой охлаждения появляется горизонтальный участок. Затем температура системы снова понижается, так как система получает степень свободы. На основании кривых температура-время строят Т-Х диаграмму состояния конденсированной системы. На диаграмму наносятся точки, отвечающие температуре начала кристаллизации и температуре конца кристаллизации сплавов. Проведя кривую через точки, отвечающие началу затвердевания сплавов, получаем на диаграмме Т-Х линию ликвидуса системы. Точки, соответствующие температуре полного затвердевания, лежат на линии солидуса.

В точке пересечения линий ликвидуса АЕ и ВЕ находится состав сплава, который имеет самую низкую температуру плавления. Эта точка носит название эвтектика. В эвтектике имеет место равновесие трех фаз: жидкость « Атв. + Втв. Равновесие фаз при этой температуре в конденсированной системе является нонвариантным, поэтому кристаллизация смеси двух твердых фаз в двухкомпонентной системе происходит при постоянной температуре. На кривой дифференциальной записи зафиксируется несколько последовательных эндоэффектов.

Для нахождения положения эвтектической точки на диаграмме используется метод Таммана, заключающийся в следующем. На основании кривых охлаждения наносят на диаграмму состояния Т-Х, для каждого сплава, длины горизонтальных участков в произвольном масштабе, которые пропорциональны количеству тепла, выделившегося при кристаллизации эвтектики. Если концы нанесенных линий соединить, то получится треугольник, называемый треугольником Таммана. На диаграмме системы с простой эвтектикой максимальная длина остановки отвечает составу эвтектики. Если компоненты претерпевают полиморфные превращения, то на кривых охлаждения могут быть обнаружены, кроме кристаллизации эвтектики и другие нонвариантные процессы и отвечающие им горизонтальные участки. Построение треугольников Таммана позволяет выяснить природу соответствующих процессов.

Кривые ликвидуса для идеальных растворов, т. е. таких растворов, у которых теплоты смешения компонентов равны нулю, могут быть построены на основании уравнения Шредера (1890 г.) — Ле-Шателье (1894 г.).

(2)

где X — мольная доля компонента А; Lf — теплота плавления (кристаллизации) компонента А. Интегрируя это уравнение получаем:

(3)

откуда , (4)

где TA — температура плавления компонента А.

Содержание

Заменив натуральные логарифмы десятичными находим
Характерные линии и области диаграммы
Диаграммы состояния двухкомпонентных сплавов
Диаграмма состояния сплавов с неограниченной растворимостью компонентов в твердом состоянии (сплавы твердые растворы с неограниченной растворимостью)
Диаграмма состояния сплавов с отсутствием растворимости компонентов в компонентов в твердом состоянии (механические смеси)
Диаграмма состояния сплавов с ограниченной растворимостью компонентов в твердом состоянии
Диаграмма состояния сплавов, компоненты которых образуют химические соединения
Диаграмма состояния сплавов, испытывающих фазовые превращения в твердом состоянии (переменная растворимость)
Связь между свойствами сплавов и типом диаграммы состояния
📽️ Видео

Заменив натуральные логарифмы десятичными находим

(5)

Уравнение может быть записано в виде:

(6)

и в общем виде (7)

Зависимость логарифма растворимость от обратной температуры для идеальных растворов выражается прямой. Несоблюдение прямолинейной зависимости может происходить отряда причин: от зависимости теплоты плавления от температуры, от образования соединений и от степени диссоциации их в расплаве. Уравнение кривой ликвидуса бинарного молекулярного раствора, в которое входит добавочный член, учитывающий зависимость теплоты плавления от энергии взаимообмена компонентов в расплаве (a), имеет вид

. (8)

Уравнение такого типа впервые выведено Ван-Лааром.

Для описания ликвидуса реальных растворов можно воспользоваться понятием активности. Подставим в уравнение Шредера-Ле-Шателье вместо Х величину активности (a)

, (9)

и учитывая, что a =gx, где g — коэффициент активности, получим:

. (10)

Активность веществ в растворе может быть определена методом измерения э. д.с. или путем исследования равновесия пар‑раствор. При определении активности методом эдс используется выражение:

(11)

где Gi — парциальная молярная свободная энергия компонента в растворе, F — число Фарадея, E — эдс.

Двойные диаграммы состояния можно разделить на несколько различных групп (или типов):

1. Системы с неограниченной растворимостью компонентов в жидком и твердом состояниях:

· с простыми кривыми ликвидуса и cолидуса;

· с максимумом или минимумом на кривых ликвидуса и солидуcа;

· c полиморфным превращением одного из компонентов;

· с разрывом растворимости компонентов в твердом состоянии.

2. Системы с неограниченной растворимостью компонентов в жидком и ограниченной растворимостью в твердом состояниях:

· эвтектического типа с постоянной и переменной растворимостью компонентов в твердом состоянии;

· перитектического типа с переменной растворимостью компонентов в твердом состоянии.

3. Системы с полной нерастворимостью или ограниченной растворимостью компонентов в жидком состоянии:

· с отсутствием растворимости компонентов в жидком и твердом состояниях;

· с ограниченной растворимостью компонентов в жидком и отсутствием растворимости в твердом состояниях;

· с монотектическим превращением.

4. Системы с различными химическими соединениями, которые образуются:

· непосредственно из жидкости;

· при взаимодействии двух жидких растворов разного состава;

· по трехфазной перитектической реакции;

· из твердого раствора;

при взаимодействии двух твердых фаз, отличных по составу от соединения.

ДИАГРАММЫ СОСТОЯНИЙ С НЕОГРАНИЧЕННОЙ РАСТВОРИМОСТЬЮ КОМПОНЕНТОВ В ЖИДКОМ И ТВЕРДОМ СОСТОЯНИЯХ

При оплавлении металлов сравнительно часто образуются непрерывные ряды жидких и твердых растворов.

Различают ряды твердых растворов трех типов:

1) твердые растворы замещения, в которых растворенные атомы или ионы замещают атомы или ионы того же заряда в принадлежащих им позициях исходной структуры;

2) твердые растворы внедрения, при образовании которых растворенные частицы — неметаллические элементы с малыми атомными объемами (углерод, азот, водород и др.) занимают позиции, вакантные в исходной структуре металла, не вытесняя при этом атомов или ионов исходной структуры;

3) твердые растворы вычитания, образующиеся, когда недостает атомов какого-либо одного типа из двух или более присутствующих в решетке. Например, вюстит Fe1-xO.

Для образования непрерывных твердых растворов необходима полная растворимость металлов в жидком состоянии. Если металлы в жидком состоянии имеют ограниченную растворимость (или она отсутствует), то между ними непрерывные твердые растворы не образуются.

Однако и при полной растворимости металлов в жидком состоянии очень часто образуются ограниченные твердые растворы или химические соединения.

Основным условием образования непрерывных растворов замещения считают химическое сходство металлов. Непрерывные растворы чаще всего образуют металлы с аналогичным строением атомов. Эти металлы имеют одинаковые (или близкие) по типу кристаллические решетки, их отношения радиусов не сильно (не более чем на 10-15 %) отличаются друг от друга. Обычно такие металлы являются химическими аналогами друг друга и располагаются в одной (реже ‑ в соседних) подгруппе периодической системы.

Таким образом, образованию непрерывных твердых растворов между металлами способствуют их благоприятные химический и размерный факторы.

Непрерывные твердые растворы не образуются, если металлы имеют разные по типу кристаллические решетки, а также при одном типе решеток, если велика разница в отношениях их радиусов и относительных электроотрицательностях.

Диаграммы состояний с непрерывными рядами жидких и твердых растворов

Простейшая диаграмма, компоненты которой образуют непрерывные (от А до В) жидкие и твердые растворы, представлена на рисунке 3.

Выпуклую вверх кривую А’135В’ принято называть линией ликвидуса (или просто ликвидусом) диаграммы. При температурах выше этой кривой все сплавы однофазны и находятся в жидком состоянии. Ликвидус диаграммы состояний показывает, как изменяется температура начала кристаллизации жидких сплавов в зависимости от их состава.

Вогнутую вниз кривую А’246В’ называют линией солидуса (или просто солидусом) диаграммы. При температурах ниже солидуса все сплавы также однофазны, но находятся в твердом состоянии. Солидус диаграммы состояний изображает температуры конца кристаллизации различных сплавов.

Рисунок 3 ‑ Диаграмма состояния двойной системы с непрерывным рядом твердых растворов

В интервале температур между кривыми ликвидуса и солидуса сплавы находятся в гетерогенном состоянии и состоят из жидкости и кристаллов L + α. Таким образом, кривые ликвидуса и солидуса позволяют выделить на диаграмме состояний три различных фазовых области: L, α и L + α.

Температурный интервал между ликвидусом и солидусом принято называть интервалом кристаллизации сплавов. Интервал кристаллизации чистых компонентов равен нулю, поскольку кривые ликвидуса и солидуса сходятся в точках, отвечающих температурам плавления металлов А и В. Двойные сплавы-растворы имеют различный интервал кристаллизации. Обычно он максимален у сплава, содержащего около 50 % компонента В.

Кривые ликвидуса и солидуса при образовании твердых растворов могут быть различного типа. Возможное расположение линий ликвидуса и солидуса системы при образовании твердого раствора теоретически выведено Розебомом (1899 г.) из рассмотрения изотерм термодинамического потенциала (свободной энергии Гиббса).

Тип 1 соответствует случаю, когда линии ликвидуса и солидуса непрерывно повышаются при увеличении в растворе концентрации компонента В (рисунок 3).

Тип 2 относится к случаям, когда на кривой ликвидуса есть максимум (рисунок 4). В экстремальной точке m` (точке максимума) кривые ликвидуса и солидуса касаются друг друга. Сплав, отвечающий точке m`, характеризуется нулевым интервалом кристаллизации и идентичностью составов жидкости и кристаллов. При затвердевании он ведет себя как чистый компонент и имеет аналогичную кривую охлаждения.

Рисунок 4 ‑ Диаграммы состояния бинарной системы с твердыми растворами 2 типа

Тип 3 относится к случаю, если на кривой ликвидуса есть минимум (рисунок 5). Кривые нагревания в этих случаях похожи на кривые для твердых растворов 1 типа Розебома (рисунок 4). В экстремальной точке m` (точке минимума) кривые ликвидуса и солидуса касаются друг друга. Сплав, отвечающий точке m`, характеризуется нулевым интервалом кристаллизации и идентичностью составов жидкости и кристаллов. При затвердевании он ведет себя как чистый компонент и имеет аналогичную кривую охлаждения.

Рисунок 5 ‑ Диаграммы состояния системы с твердыми растворами 3 типа по Розебому

Твердые растворы 4 типа по Розебому (растворы с перитектикой). Если прибавление к компоненту А компонента В вызывает повышение температуры сплава, то на диаграмме температура называется перитектической, а точка Р на Т-Х — диаграмме — перитектикой или переходной. На рисунке 6 изображена схема диаграммы систем, в которых твердые растворы образуют перитектику.

При перитектической температуре при охлаждении системы происходит следующее взаимодействие фаз: L + aтв ®bтв. При нагревании процесс идет в обратную сторону: bтв ®L + aтв.

Рисунок 6 ‑ Диаграммы состояния бинарной системы с твердыми растворами 4 типа по Розебому

Диаграмма может быть выведена из диаграммы системы с непрерывным рядом растворов (рисунок 7 а). Чтобы убедиться в этом, представим себе, что внутри области твердых растворов образуется область несмешиваемости (рисунок 7 б): выше критической температуры существуют однофазный твердый раствор, а ниже ‑ двухфазная смесь твердых растворов. Далее пусть купол несмешиваемости растет в сторону высоких температур и, наконец, пересекает кривую солидуса. В итоге получим диаграмму, показанную на рисунке 7 в.

Рисунок 7 – Бинарная система эвтектического типа с ограниченной взаимной растворимостью компонентов

Более сложная фазовая диаграмма, включающая инконгруэнтно плавящееся соединение, на основе которого образуются ограниченные твердые растворы, приведена на рисунке 8. Схемы а—г на том же рисунке показывают эволюцию диаграммы при последовательном «введении» твердых растворов на основе соединения (б) и компонентов (вид); эти построения учитывают, что при температурах солидуса Т1 и Т2 области твердых растворов должны иметь максимальную ширину.

Рисунок 8 – Бинарная система с инконгруэнтно плавящимся соединением и твердыми растворами ограниченной протяженности

Твердые растворы эвтектического типа (5 типа по Розебому). Если в системе образуются ограниченные растворы и от прибавления к одному из компонентов другого температура начала кристаллизации сплавов понижается, то на Т-Х диаграмме системы имеется эвтектика. На рисунке 9 изображена система, в которой твердые растворы образуют эвтектику.

Рисунок 9 ‑ Диаграмма состояния двухкомпонентной системы с твердыми растворами 5 типа по Розебому

Максимальная растворимость компонента В в кристаллах А зависит от температуры и определяется кривой хтр. При тепературе, чуть меньшей, чем температура плавления А, растворимость В в твердом А незначительна, и уже при небольшой концентрации В состав соответствует двухфазной области смесей расплав + Атв. р. (где Атв. р. ‑ твердый раствор на основе компонента А). С понижением температуры область растворимости постепенна расширяется, и максимальная растворимость наблюдается при температуре солидуса в точке т. Такова общая закономерность систем с твердыми растворами. При дальнейшем понижении температуры растворимость В в кристаллах А уменьшается вдоль кривой тх. Кристаллы В также растворяют в себе компонент А, и предельная растворимость меняется вдоль кривой ynq. Область твердых растворов А в В менее обширна, чем растворов В в А, максимум же растворимости вновь наблюдается при температуре солидуса (точка п).

Состав твердого раствора Атв. р в двухфазной области (Атв. р + Втв. р) определяется пересечением конноды при интересующей температуре, например Т1 с кривой тх, ограничивающей область Атв. р; пересечение той же конноды и кривой пу определяет состав сосуществующего твердого раствора Втв. р.

Во многих диаграммах твердые фазы представлены как линейные фазы, т. е. фазы с фиксированной стехиометрией без области гомогенности или без образования твердых растворов (рисунок а). В действительности же составы этих фаз могут меняться в узком интервале (рисунок б), но обнаружить изменения, а также установить интервал существования данной фазы иногда бывает трудно.

Кривые нагревания веществ с ограниченной растворимостью могут не иметь пиков. И для определения линий ликвидуса используется метод Байкова, основанный на определении температур, при которых наблюдается частичное подплавление сплавов, состав которых известен. Для определения границ твердого раствора готовят серию сплавов, содержащих возрастающее количество добавленного компонента и нагревают их некоторое время при температуре эвтектики, затем производят закалку сплавов и исследуют под микроскопом шлифы этих сплавов. Сплавы, состав которых лежит в области твердого раствора, имеют однородную, характерную для твердого раствора структуру. На микроструктуре сплавов, составы которых находятся в гетерогенной области (жидкость + твердый раствор), наблюдается подплавление образцов.

Серии сплавов такого же состава нагревают при более высоких температурах, и после закалки исследуют их микроструктуру. Составы сплавов, у которых обнаруживается начало подплавления, лежат на границе твердого раствора с гетерогенной областью. На рисунке 10 приведена схема построения этим методом границы твердого раствора.

Рисунок 10 ‑ Построение границы твердого раствора с помощью метода Байкова

Если компоненты имеют несколько модификаций, то вид диаграммы двухкомпонентных систем зависит от типа твердых растворов, которые образуют эти модификации.

Могут быть непрерывные твердые растворы на основе обеих модификаций (рисунок 11).

Рисунок 11 ‑ Диаграмма состояния двухкомпонентной системы при наличии у обоих компонентов полиморфных модификаций, образующих непрерывные твердые растворы

На рисунке 12 приведена система, в которой полиморфное превращение α↔β имеется только у компонента В. Компоненты А и В образуют непрерывный твердый раствор. При температуре Т2 компонент В испытывает α↔β превращение. Модификация β образует с компонентом А ограниченный твердый раствор. Температура начала и конца превращения понижается до пересечения с осью абсцисс, на диаграмме появляется двухфазная область α↔β.

Рисунок 12 ‑ Диаграмма состояния двухкомпонентной системы, если у одного из компонентов есть полиморфное превращение

На рисунке 13 показано превращение твердого раствора по эвтектоидной схеме. В этой системе сначала кристаллизуется непрерывный твердый раствор на основе a-модификации обоих компонентов. При температуре превращения он распадается на два твердых раствора b и b’. После распада твердого раствора α состав b и b’ твердых растворов изменяется при понижении температуры по кривым ag и bd.

Рисунок 13 ‑ Диаграмма состояния двухкомпонентной системы: a-модификации компонентов образуют непрерывный твердый раствор, b-модификации претерпевают эвтектоидное превращение

На рисунке 14 изображена система, в которой высокотемпературные a-модификации обоих компонентов образуют непрерывный ряд твердых растворов, а низкотемпературные b и b’-модификации ограниченные твердые растворы. Температура превращения a + b’ «b лежит при Т3 между температурами чистых компонентов. Такого типа превращения носит перитектоидных характер. Температура, при которой происходит такое превращение называется перитектоидной.

Рисунок 14 ‑ Диаграмма состояния бинарной системы: a-модификации компонентов образуют непрерывные твердые растворы, а низкотемпературные b и b’-модификации — ограниченные твердые растворы

Могут быть и другого рода превращения твердых растворов. На рисунке 15 приведена диаграмма состояния, на которой высокотемпературные модификации образуют ограниченные растворы, а низкотемпературные — непрерывный твердый раствор.

Рисунок 15 ‑ Диаграмма состояния системы, в которой высокотемпературные модификации образуют ограниченные твердые растворы, а низкотемпературные — неограниченные твердые растворы

На рисунке 16 приведена диаграмма состояния системы, в которой компонент А — имеет одну модификацию, а компонент В — две. Превращение твердых растворов a« L + b происходит по перитектической схеме, a — модификация образует непрерывный твердый раствор. Могут быть и еще более сложные превращения.

Рисунок 16 ‑ Диаграмма состояния системы, в которой компонент А имеет одну модификацию, а компонент В — две

Зависимость концентрации твердых растворов от температуры описывается уравнением Шредера-Ле-Шателье:

(12),

где a и b — постоянные; х — концентрации твердого раствора.

Если при двух температурах определить концентрации твердого раствора (х1 и х2) и найти значения а и b, то можно построить кривую солидуса, откладывая по оси абсцисс lgх, а по оси ординат 1/Т. Кривую солидуса в системе с идеальными твердыми растворами можно построить, используя уравнение Ван-Лаара

(13),

где хA — мольная доля компонента А в твердом растворе; х’A — мольная доля компонента А в расплаве; Т — температура равновесия между жидкой и твердой фазами; ТA — температура плавления компонента А; LA — можно рассчитать из выражения:

(14)

где M — молекулярная масса; w — доля не ассоциированных жидкостей.

Видео:ДИАГРАММА СОСТОЯНИЯ ЖЕЛЕЗО-ЦЕМЕНТИТ, железо-углерод, Fe+Fe3CСкачать

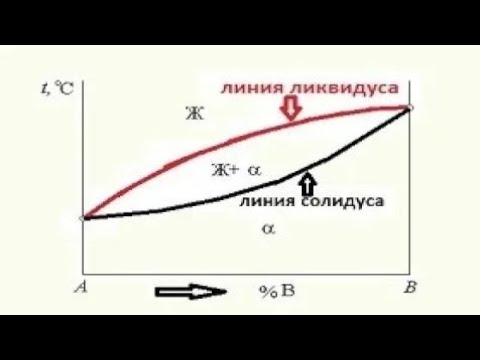
Характерные линии и области диаграммы

ABCD — линии ликвидус — линия начала процесса кристаллизации Выше линии ликвидус (область I) сплав находится в жидком состоянии и представляет собой однородную систему — жидкий раствор.

AHJECF — линия солидус — линия завершения процесса кристаллизации. Сплавы, лежащие ниже этой линии, находятся в твёрдом состоянии. При температурах между линиями ликвидус и солидус происходит кристаллизация сплавов. В период кристаллизации одновременно существуют две фазы — жидкий расплав и кристаллы твёрдых растворов.

Рассматривая линию ликвидус ABCD, можно отметить, что с увеличением содержания углерода С в железе до 4,3% температура плавления сплава понижается, а с дальнейшим повышением содержания углерода (участок CD) температура плавления сплава увеличивается.

На участке линии ликвидус АВ выделяются кристаллы δ-твёрдого раствора (феррита Ф), состав которых определяется линией АН. Состав жидкой фазы изменяется по линии АВ. Предельную растворимость углерода (0,1%) в δ-железе Fe_δ (феррите Ф) при температуре 1493°С показывает точка Н.

На участке АН заканчивается кристаллизация феррита Ф. На линии HJB при постоянной температуре 1499°С жидкая фаза, содержащая 0,5% С (точка В), реагирует с ранее выпавшими кристаллами δ-твёрдого раствора (феррита Ф), что приводит к образованию кристаллов нового вида. Реакцию подобного вида называют перитектической (перитектическое превращение). В результате этой реакции образуются кристаллы аустенита А, содержащего 0,18% С (точка J):

По линии HN начинается превращение феррита Ф(δ) в аустенит А, обусловленное полиморфным превращением железа. По линии NJ заканчивается превращение феррита Ф(δ) в аустенит А.

По линии ВС при понижении температуры из расплава выпадают кристаллы аустенита А переменного состава, с меньшим содержанием углерода (от 0,5 до 2,14%), чем в жидкой фазе, из которой они выделяются. Изменение состава жидкой фазы с понижением температуры происходит по линии ВС (линия ликвидус), а выпавших кристаллов — по линии JE (линия солидус). На участке JЕ заканчивается кристаллизация аустенита А.

Таким образом, если сплавы содержат до 2,14% С, то их кристаллизация заканчивается при температуре выше 1147°С, где жидкая фаза обогащается углеродом до 4,3%. Одновременно из расплава выпадают кристаллы аустенита, содержащие 2,14% С (точка Е) и цементита, содержащего 6,67% С (точка F).

На участке ECF при постоянной температуре 1147ºС идёт эвтектическое превращение, заключающееся в том, что жидкость, содержащая 4,3% углерода превращается в эвтектическую смесь аустенита А и цементита первичного Ц_І:

Ледебурит (Л) (точка С) — механическая эвтектическая смесь (эвтектика) кристаллов аустенита А и цементита Ц, содержащая 4,3% C. Эвтектика системы железо — цементит называется ледебуритом Л, по имени немецкого учёного Ледебура.

Сплавы, лежащие праве точки С, т. е. содержащие от 4,3 до 6,67% С, кристаллизуются по линии CD. В процессе их кристаллизации выделяется первичный цементит Fe₃C (Ц_I). По мере образования из жидкого расплава первичного цементита (Ц _I) содержание углерода в жидкой фазе уменьшается.

При температуре 1147°С (линия CF) оставшийся расплав содержит 4,3% С и затвердевает с образованием ледебурита (эвтектики). В результате окончательно затвердевший сплав (ниже линии CF) состоит из первичного цементита (ЦI) и ледебурита Л.

Сплавы, находящиеся левее точки С, т. е. содержащие до 4,3% С, называются доэвтектическими, а сплавы находящиеся правее от точки С, т. е. содержащие более 4,3% С, — заэвтектическими. Между линиями ликвидус ABCD и солидус AHJECF (области II и III) железоуглеродистые сплавы состоят из жидкой и твёрдой фаз, причём с понижением температуру количество твёрдой фазы увеличивается.

Таким образом, непосредственно после окончания затвердевания структура доэвтектических сплавов состоит из аустенита А и ледебурита Л, структура эвтектического сплава — из ледебурита Л и структура заэвтектического сплава — из первичного цементита (Ц _I) и ледебурита Л.

Ниже линии солидус AHJECF в затвердевших сплавах при понижении температуры наблюдается дальнейшее изменение их структуры, связанное с перекристаллизацией в твёрдом состоянии. Такие изменения называют вторичной кристаллизацией. С понижением температуры железо переходит из одной модификации в другую (Fe_γ → Fe_α) и растворимость углерода в γ-железе Fe_γ и α-железе Fe_α заметно уменьшается.

По линии PSK при постоянной температуре 727ºС идёт эвтектоидное превращение, заключающееся в том, что аустенит А, содержащий 0,8% углерода С, превращается в эвтекто-идную смесь феррита Ф и цементита вторичного Ц_II:

По механизму данное превращение похоже на эвтектическое, но протекает в твёрдом состоянии. Эвтектоид системы железо — цементит называется перлитом (П), он содержит 0,8% углерода С. Название такое эта фаза получила за то, что на полированном и протравленном шлифе наблюдается перламутровый блеск. Перлит может существовать в зернистой и пластинчатой форме, в зависимости от условий его образования.

Доэвтектические сплавы (до 2,14% С) в области IV состоят из одного аустенита А При охлаждении сплавов, содержащих менее 0,8% С (левее точки S), ниже линии GOS происходит распад аустенита А с выделением из него избыточного феррита Ф, что обусловлено полиморфным превращением железа Fe. Так как феррит Ф, выделяющийся при охлаждении аустенита А по линии GOS, содержит не более 0,02% С (предельная растворимость углерода в α-железе Fe_α, точка Р), аустенит А несколько обогащается углеродом С, изменяя состав по линии GS. Кристаллы феррита изменяют свой состав по линии GOS.

Такой процесс протекает до температуры 727°С. В точке S при 0,8% С аустенит А распадается на твёрдую эвтектоидную механическую смесь кристаллов феррита Ф и цементита Ц, называемую перлитом П. Пользуясь правилом отрезков по диаграмме состояния, можно определить соотношение феррита Ф и цементита Ц в перлите при 727°С

где Q — количество вещества.

Внешне зерно перлита состоит из параллельных пластинок феррита и цементита. Чем грубее и крупнее выделения цементита, тем хуже механические свойства перлита.

Сплавы, содержащие 0,8% С называются эвтектоидными, содержащие менее 0,8% С — доэвтектоидными, и содержащие более 0,8% С — эаэвтектоидными.

При охлаждении сплавов, лежащих правее точки S и содержащих более 0,8% С, ниже линии SE происходит распад аустенита А с выделением из него вторичного цементита Ц_II, обусловленный снижением растворимости углерода в аустените при понижении температуры. Так как выделяющийся вторичный цементит Ц_II содержит 6,67% С, концентрация углерода в остающимся аустените А изменяются (уменьшается) по линии SE до состава точки S (0,8% С) при 727°С.

Таким образом, доэвтектоидные сплавы в области VIII состоят из аустенита А и феррита Ф, а в области IX — из феррита Ф и перлита П. Заэвтектоидные сплавы (0,8 — 2,14% С) в области V состоят из аустенита А и вторичного цементита Ц_II, а в области Х — из вторичного цементита Ц_II и перлита П.

Сплавы, содержащие от 2,14 до 4,3% С, выше линии PSK, но ниже линии ECF (область VI) состоят из аустенита А, вторичного цементита Ц_II и ледебурита Л.

По линии PSK и ниже в этих же сплавах (область XI) происходит превращение аустенита А в перлит П; структура сплава состоит из перлита П, цементита Ц и вторичного ледебурита Л_II. Сплавы, соответствующие эвтектической точке С, ниже линии PSK имеют структуру одного ледебурита Л.

Сплавы, содержащие 4,3 — 6,7% С, ниже линии CF, но выше линии PSK (область VII) состоят из цементита Ц и первичного ледебурита Л_I; ниже линии PSK (область XII) сплавы сохраняют эту же структуру.

По линии PG происходит превращение аустенита А в феррит Ф заканчивается. Также в нижней левой части диаграммы линия PQ показывает уменьшение растворимости углерода в α-железе Fe_α (феррите Ф) с понижением температуры. По линии PQ из феррита Ф начинается выделение третичного цементита Ц_ІІІ, обусловленное снижением растворимости углерода в феррите при понижении температуры. Следовательно, сплавы между точками Р и Q состоят из феррита Ф и третичного цементита Ц_ІІІ.

Сплавы, находящиеся внутри области GPQ, состоят только из феррита Ф.

По линии МО при постоянной температуре 768ºС имеют место магнитные превращения сплава.

Температуры, при которых происходят фазовые и структурные превращения в сплавах системы железо — цементит, т. е. критические точки, имеют условные обозначения.

Обозначаются они буквой А (от французского arret — остановка):

A₂ — линия MO (768ºС, — точка Кюри — магнитные превращения);

A₃— линия GOS (переменная температура, зависящая от содержания углерода в сплаве) — превращение Ф ↔ А;

A₄ — линия NJ (переменная температура, зависящая от содержания углерода в сплаве)

A_cm — линия SE (переменная температура, зависящая от содержания углерода в сплаве)

— начало выделения цементита вторичного Ц_ІІ (иногда обозначается A3).

Так как при нагреве и охлаждении превращения совершаются при различных температурах, чтобы отличить эти процессы вводятся дополнительные обозначения. При нагреве добавляют букву с, т. е. А_с1, при охлаждении — букву r, т. е. А_r₁.

Все сплавы, характеризующиеся диаграммой Fe-C, разделяют на: техническое железо (

Дата добавления: 2014-12-08 ; просмотров: 2600 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Солидус, ликвидус и ледебуритСкачать

Диаграммы состояния двухкомпонентных сплавов

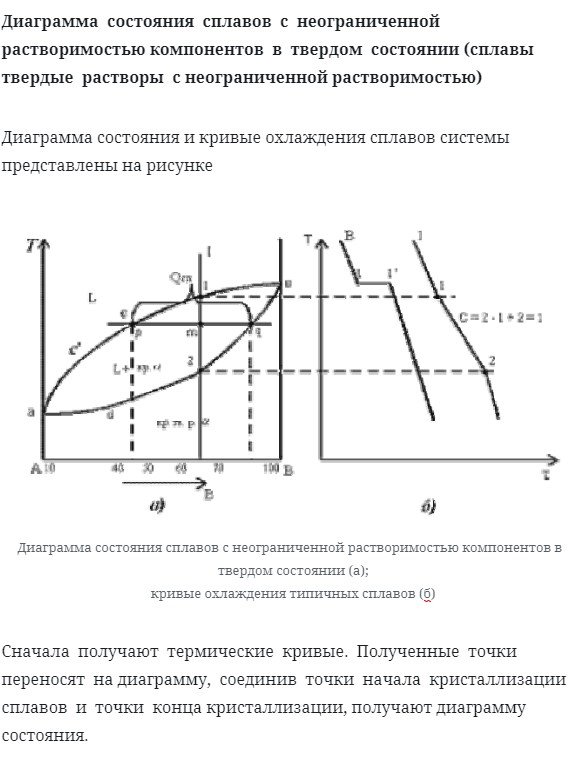
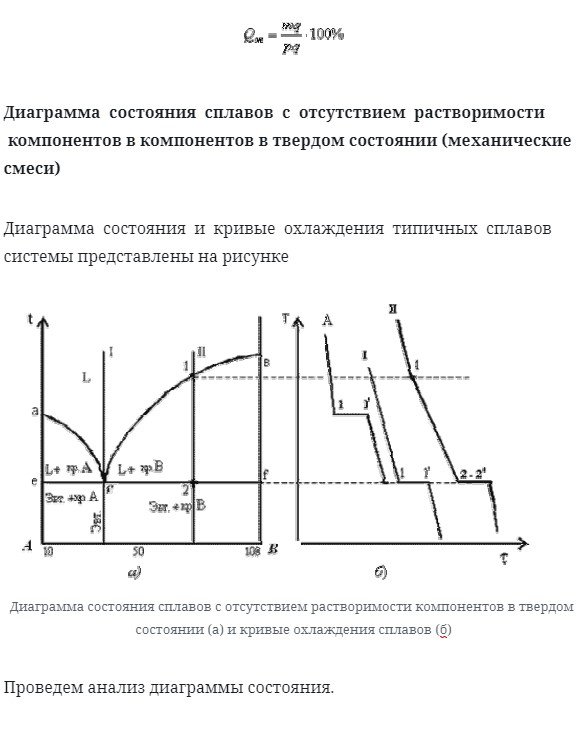
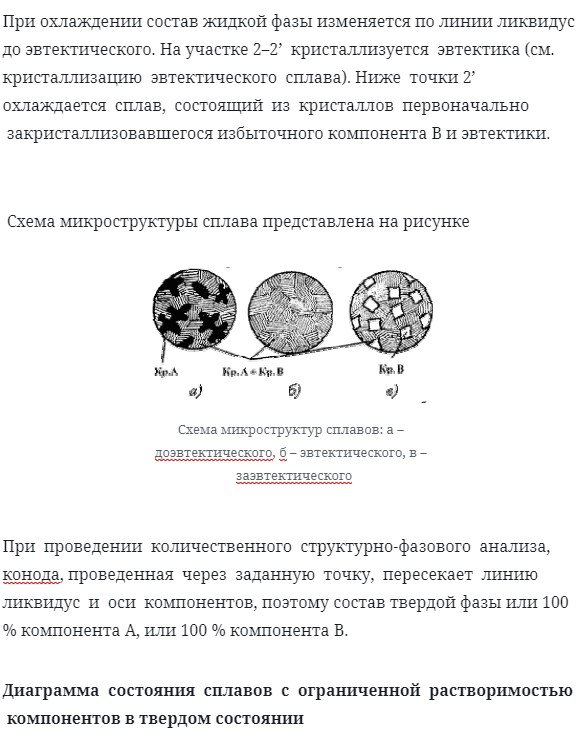
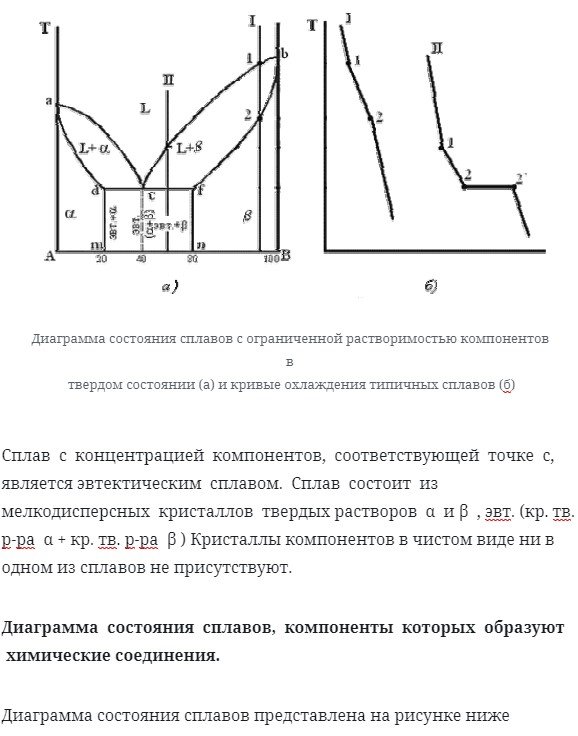
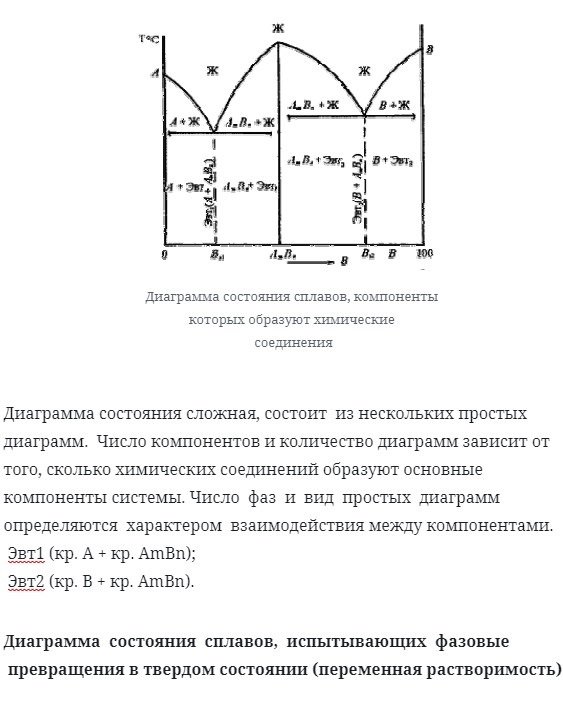
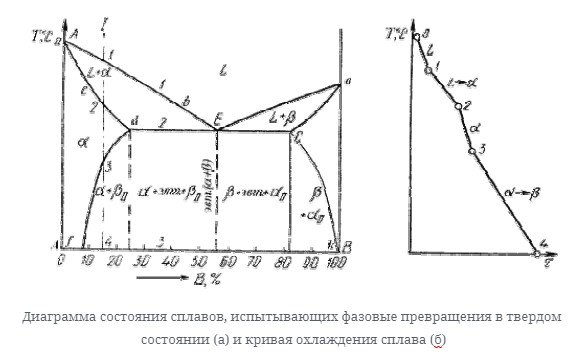
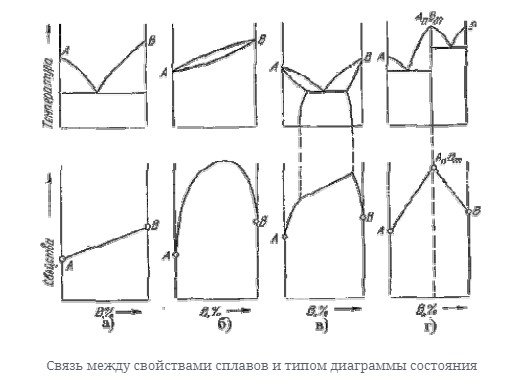
Диаграмма состояния представляет собой графическое представление фазового состояния сплава и его критической точки в зависимости от температуры и концентрации в равновесии.

Показывает состояние сплава с изменениями температуры, давления и химического состава.

Фазовая диаграмма служит основой для определения фазового превращения, состава и количества фаз, структурных составляющих сплава, определяющих его механические, физические, химические и технические свойства.
Собственность.

Диаграмма состояния представляет собой 1 из основных компонентов при синтезе нового сплава. Они позволяют прогнозировать механические и технические характеристики, разрабатывать технологические процессы литья, термообработки и пластической обработки 1 или другого сплава.

Видео:09 Фаз диагр двухкомп сист 1 принципы и мех смесьСкачать

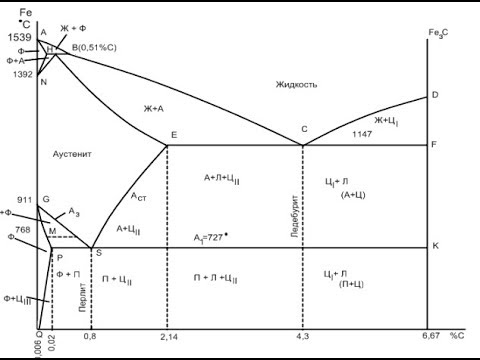
Диаграмма состояния сплавов с неограниченной растворимостью компонентов в твердом состоянии (сплавы твердые растворы с неограниченной растворимостью)

Диаграмма состояния и кривые охлаждения сплавов системы представлены на рисунке

Сначала получается тепловая кривая. Полученная точка переносится на диаграмму и приобретает диаграмму состояния, соединяющую начальную точку кристаллизации сплава и конечную точку кристаллизации.

Давайте проанализируем полученную цифру.

Количество компонентов: k = 2 (компоненты a и b).
Количество фаз: f = 2 (жидкий l, твердый раствор Кристалла）
Основная линия на рисунке: acb-это линия Ликвидуса, а сплав над этой линией-жидкое состояние. АДБ Солидус, и сплав под этой линией в твердом состоянии.

Характеристика сплава системы：

Чистые компоненты а и в кристаллизуются при постоянной температуре. Кривая охлаждения компонента в представлена на рисунке. 5. 1, б.
Остальные сплавы кристаллизуются так же, как и сплав i. Кривая охлаждения показана на рисунке 1. 5. 1, б.
Процесс кристаллизации сплава i: до пункта 1, Сплав охлажен в жидкости state. At при температуре, соответствующей точке 1, начинает формироваться центр кристаллизации твердого раствора α.

Точка перегиба (критическая точка) регистрируется на кривой охлаждения, что связано с уменьшением скорости охлаждения за счет выделения скрытой теплоты crystallization. In разделы 1-2, процесс кристаллизации продолжается с уменьшением в temperature. In в соответствии с фазовым законом 2-компонентной системы, в присутствии 2-фазы (жидкого и α-твердого раствора кристалла) число степеней свободы равно 1.

При достижении температуры соответствующей точке 2 сплав затвердевает, а при дальнейшем понижении температуры сплав в твердом состоянии охлаждается, состоящий из однородных кристаллов α-твердого раствора.

Количественный структурно-фазовый анализ сплава.
Используя диаграмму состояния, можно определить не только количество фаз, но и их состав и количественное соотношение в сплаве при любой температуре. Для этого используйте правила сегмента. Для количественного структурно-фазового анализа горизонталь (конус) рисуется в заданной точке до пересечения с ближайшей линией на диаграмме (Ликвидус, Солидус или ось компонентов).

Определение фазового состава в точке m：
Чтобы определить его, проведите горизонтальную линию через точку m, пока она не пересечется с Ликвидусом и Солидусом, которые являются ближайшими линиями на диаграмме. Состав жидкой фазы определяется проекцией горизонтального пересечения с линией Ликвидуса р на концентрационную ось.
Состав твердой фазы определяется проекцией горизонтального пересечения с линией Солидуса q (или осью компонента) на ось концентрации. Состав жидкой фазы изменяется вдоль линии Ликвидуса, в то время как состав твердой фазы изменяется вдоль линии Солидуса. При понижении температуры фазовый состав изменяется в сторону уменьшения содержания компонента В.

б) определение количественного соотношения жидкой и твердой фаз при заданной температуре (точка м) ：
Количественная масса фазы обратно пропорциональна сегменту коноды. Рассмотрим точку m и конус, проходящий через ее сегмент. Количество всего сплава (qsp) определяется сегментом pq.

Линия, примыкающая к Ликвидусу pm, определяет количество твердой фазы. Сегмент mq, примыкающий к Солидусу (или компонентной оси), определяет количество жидкой фазы.

Видео:Диаграмма "железо-углерод". Кривые охлаждения. Лабораторная работаСкачать

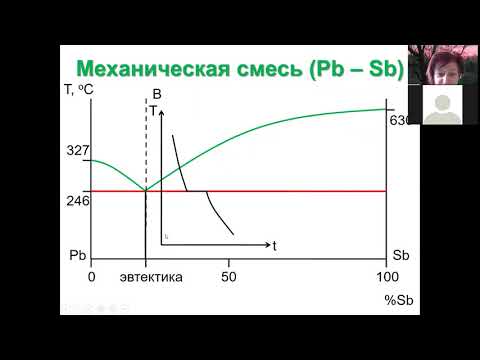
Диаграмма состояния сплавов с отсутствием растворимости компонентов в компонентов в твердом состоянии (механические смеси)

Диаграмма состояния и кривые охлаждения типичных сплавов системы представлены на рисунке

Проведем анализ диаграммы состояния. Количество компонентов: k = 2 (компоненты a и b).
Количество фаз: f = 3 (Кристалл компонента a, Кристалл компонента b, жидкая фаза).
Основная линия графика：
* Линия liquidus line состоит из acb, 1 точка сходится на 2 ветви.
* Линии солидуса ecf, параллельные оси концентрации, стремятся к оси компонентов, но не достигают их •
Типичный сплав системы.
а) чистые компоненты, кристаллизуются при постоянной температуре, на рис 5. 3 б показана кривая охлаждения компонента А.
б) эвтектический сплав-сплав, соответствующий концентрации компонентов точки с (сплав i). Кривая охлаждения этого сплава подобна кривой охлаждения.
5. 3 Б) эвтектика-тонкоизмельченная механическая смесь разнородных кристаллов, которые кристаллизуются одновременно при постоянной температуре, самой низкой для рассматриваемой системы .

При образовании сплавов из механических смесей эвтектика состоит из компонентов а и кристаллов в: эвтектика. (возврат каретки. Возврат каретки.）

Эвтектический процесс кристаллизации сплава:к пункту 1, Сплав охлажен в жидкости state. At при температуре, соответствующей точке 1, начинается одновременная кристаллизация 2-х различных компонентов. Кривая температуры отмечена на кривой охлаждения. Процесс протекает при постоянной температуре. Это объясняется тем, что число степеней свободы становится равным нулю по фазовому закону 2-компонентной системы, в которой имеется 3 фазы (жидкости и кристаллы компонентов А и в).

В точке 1 / процесс кристаллизации завершен. Менее 1 балла/
Сплав охлаждается и состоит из неоднородно дисперсных кристаллов компонентов a и b. C) другие сплавы в системе аналогичны сплаву ii. Рисунок 5. 3. См. Кривую охлаждения сплава для процесса кристаллизации b. alloy ii: до пункта 1, Сплав охлажен в жидкости state. At при температуре, соответствующей точке 1, начинает формироваться центр кристаллизации избытка b, а на кривой охлаждения наблюдается точка перегиба (критическая точка), которая связана с уменьшением скорости охлаждения за счет выделения скрытой теплоты crystallization. In разделы 1-2, процесс кристаллизации продолжается с уменьшением в temperature. In в соответствии с фазовым законом 2-компонентной системы, при наличии 2-фазы (жидкой и компонента в-кристалла) число степеней свободы равно 1.

При охлаждении состав жидкой фазы изменяется на эвтектический по линии Ликвидуса. В области 2-2 происходит кристаллизация эвтектики (см. Кристаллизация эвтектического сплава). Ниже пункта 2 сплав, состоящий из кристаллов, сначала охлаждается.
Избыток кристаллизованного компонента В и эвтектики.

Схема микроструктуры сплава представлена на рисунке

При проведении количественного структурно-фазового анализа конноды, проведенные через определенные точки, пересекают линию Ликвидуса и ось компонента, поэтому состав твердой фазы составляет 100% компонента А или 100%компонента В.

Видео:Лекция «Диаграмма состояния двухкомпонентных сплавов»Скачать

Диаграмма состояния сплавов с ограниченной растворимостью компонентов в твердом состоянии

Диаграмма состояния и кривые охлаждения типичных сплавов системы представлены на рисунке ниже

Количество компонентов: k = 2 (компоненты a и b).
Количество фаз: f = 3 (жидкая фаза твердого раствора и Кристалл (раствор компонента а компонента А) и (раствор компонента а компонента Б））;
Основная линия графика：
* Линия состоит из двух ветвей, сходящихся в 1 точке линии Ликвидуса, 2.
* Стереоскопическая линия adcfb. It состоит из 3-х секций.
* dm-линия максимальной концентрации компонента b компонента a.
* fn-линия максимальной концентрации компонента a компонента b.
Типичный сплав системы.

При концентрации компонента, не превышающей предельных значений (сечения am и nâ), сплав кристаллизуется так же, как и сплав, содержащий твердый раствор с неограниченной растворимостью. См. Кривую охлаждения для сплава i на рисунке 1. Если концентрация компонента 5. 5 b превышает предел (в разделе dcf）

Сплав кристаллизуется как сплав в механической смеси. См. Кривую охлаждения сплава ii На рисунке 2. 5. 5 б

Сплав с концентрацией компонентов, соответствующей точке С, является эвтектическим сплавом. Сплав состоит из мелкодисперсных кристаллов твердых растворов α и β. (возврат каретки. Твердый раствор α+Красный твердый раствор β) кристаллов компонента в чистом виде не существует ни в одном сплаве.

Видео:Солидус, ликвидус и ледебуритСкачать

Диаграмма состояния сплавов, компоненты которых образуют химические соединения

Диаграмма состояния сплавов представлена на рисунке ниже

Диаграмма состояний является сложной и состоит из нескольких простых диаграмм. Количество компонентов и число фигур зависит от количества соединений, составляющих основные компоненты системы. Количество фаз и внешний вид простого чертежа определяются характером взаимодействия между компонентами.
eut1 (КР. Возврат каретки. Ambn）;
eut2 (КР. Б + СГ. Амбн).

Видео:Диаграмма состояния сплавов системы «железо-углерод»Скачать

Диаграмма состояния сплавов, испытывающих фазовые превращения в твердом состоянии (переменная растворимость)

Диаграмма состояния показана на рисунке.
По внешнему виду этот рисунок напоминает диаграмму состояния сплава, в котором растворимость компонентов в твердом состоянии ограничена. Разница заключается в том, что линия конечной растворимости компонента не перпендикулярна оси концентрации. При понижении температуры появляется область, в которой вторичная фаза осаждается из однородного твердого раствора.

df-линия переменной конечной растворимости компонента b в компоненте a.
ЭК является линией переменной окончательной растворимость компонента а в компоненте В.

Кривая охлаждения сплава I представлена на рисунке ниже.

Процесс кристаллизации сплава i: до пункта 1, Сплав охлажен в жидкости state. At при температуре, соответствующей точке 1, центр кристаллизации твердого раствора α начинает form. In разделы 1-2, процесс кристаллизации продолжается по мере того как температура уменьшает. Когда вы достигнете

При температуре, соответствующей точке 2, сплав затвердевает, а при дальнейшем понижении температуры сплав охлаждается в твердом состоянии, состоящем из однородных кристаллов твердого раствора α.

При достижении температуры, соответствующей точке 3, оказывается, что твердый раствор α насыщен компонентом в, а при низких температурах растворимость 2-го компонента снижается, поэтому из Альфа-раствора начинают осаждаться избыточные компоненты в виде кристаллов βn. После пункта 3, сплав кристаллы α твердого раствора и
Вторичный Кристалл βn твердого раствора

Видео:ДИАГРАММА ЖЕЛЕЗО-УГЛЕРОД [МАТЧАСТЬ]Скачать

Связь между свойствами сплавов и типом диаграммы состояния

Вид диаграммы и свойства сплава зависят от соединений или фаз, образующих компоненты сплава, поэтому между ними должна быть определенная связь. Эта зависимость установлена крнаковым на рисунке ниже.

примеры решения задачи	Лекции
Расчёт найти определения	Учебник методические указания

С образованием механических смесей свойства изменяются линейно. Величина свойств сплава лежит в интервале между свойствами чистого компонента.
При образовании твердого раствора без ограничения по растворимости свойства сплава изменяются в криволинейной форме, а некоторые свойства, такие как электрическое сопротивление, могут существенно отличаться от свойств компонента.
При образовании твердого раствора с ограниченной растворимостью характеристики диапазона концентраций, соответствующего однофазному твердому раствору, изменяются по закону кривой, а в двухфазной области изменяются по закону linearity. In кроме того, крайняя точка на линии является свойством очень насыщенного твердого раствора, который образует чистую фазу, эту смесь.
При образовании соединения концентрация соединения соответствует максимальному значению на кривой. Эта точка разрушения, соответствующая соединению, называется сингулярностью.