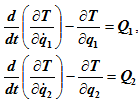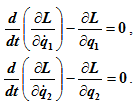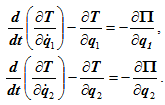Уравнения лагранжа ii рода для механической системы с двумя степенями свободы (6 видео)

iSopromat.ru

Рассмотрим уравнения Лагранжа второго рода для механической системы имеющей две степени свободы:
В случае если механическая система имеет две степени свободы ( s = 2), положение этой системы определяется двумя обобщенными координатами q₁ и q₂, которым соответствуют обобщенные силы Q₁ и Q₂.
Уравнения Лагранжа второго рода для такой системы будут выглядеть так

В случае если система является консервативной (т.е. все активные силы, действующие на систему, являются потенциальными), то уравнения Лагранжа второго рода для такой системы будут иметь вид

Для решения задач часто более удобна эквивалентная форма записи:

Чтобы составить уравнения Лагранжа второго рода для системы с двумя степенями свободы, следует действовать в такой последовательности:

сделать рисунок, обозначить на нем все активные силы, приложенные к системе;
выбрать обобщенные координаты q₁ и q₂. Рекомендации по выбору обобщенной координаты для случая системы с одной степенью свободы остаются в силе и для этого случая;
определить, является ли рассматриваемая система консервативной;
если система является консервативной, следует вычислить ее кинетическую T и потенциальную Π энергии, выразив их через обобщенные координаты q₁ и q₂ и обобщенные скорости q₁‘ и q₂‘. Если система не является консервативной, следует вычислить только ее кинетическую энергию;

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Содержание

Уравнения Лагранжа второго рода
Уравнение Лангранжа второго рода
Уравнение Лангранжа второго рода
📺 Видео

Видео:Система с двумя степенями свободыСкачать

Уравнения Лагранжа второго рода

При моделировании сложных технических систем применяют уравнения Лагранжа второго рода. Их можно использовать при построении математических моделей объектов любой физической природы, если они рассматриваются как системы с сосредоточенными параметрами. При этом никаких ограничений на структуру и физические свойства объекта не накладывается.

Уравнения Лагранжа второго рода для системы с голономными связями имеют вид

где Е_к — кинетическая энергия системы; q_t — обобщенная координата; q_t — обобщенная скорость; Q_t -— обобщенная сила; п — число степеней свободы системы.

В качестве обобщенных координат выбирают независимые между собой переменные, которые позволяют полностью определить состояние исследуемой системы. Обычно в качестве обобщенных координат и обобщенных скоростей принимают фазовые координаты типа потока. Обобщенные скорости для объектов различной физической природы приведены в табл. 3.2. Например, для механических систем обобщенными координатами выбирают линейные и угловые перемещения, а обобщенными скоростями — линейные и угловые скорости. В этом случае обобщенные силы сохраняют свой физический смысл и представляют собой силы и вращающие моменты.

Каждой обобщенной координате q_t соответствует своя обобщенная сила Q_t. Работу всех обобщенных сил на возможных перемещениях системы (виртуальную работу) можно вычислить по формуле

где bq_t — вариация i-й обобщенной координаты; 5W^ — работа г-й обобщенной силы на возможном перемещении.

Из формулы (4.80) следует, что обобщенные силы представляют собой коэффициенты при вариациях обобщенных координат в выражении для виртуальной работы.

Так как вариации обобщенных координат 5q_t независимы, то, вычисляя работу всех приложенных к системе сил на одном из возможных перемещений 8 а ^М-

Если формулы связей декартовых и обобщенных координат не содержат явно времени t, то -Е_к0 = E_Ki = О, Е_к = ?_к2. Следовательно, при стационарной структуре системы кинетическая энергия представляется однородной квадратичной формой

где тij — элемент матрицы параметров инерционных элементов системы.

Обобщенные силы можно разделить на потенциальные Q_n, диссипативные Q_r и произвольные Q*.

Силы называются потенциальными, если существует положительно определенная функция обобщенных координат, удовлетворяющая равенствам

В стационарном равновесном состоянии системы E_n = min, следовательно, 5Е_п = 0 и 5 2 Е_п >0. В окрестности точки, соответствующей этому состоянию в фазовом пространстве, потенциальная энергия может быть представлена квадратичной формой

где Cij — элемент матрицы параметров упругих элементов системы.

Обобщенные силы называют диссипативными, если существует положительно определенная функция обобщенных скоростей, удовлетворяющая равенствам

где Ф — диссипативная функция Рэлея:

(X_iy— — элемент матрицы параметров диссипативных элементов системы.

Обобщенная сила Q_t, соответствующая i-Pi обобщенной координате, равна алгебраической сумме произвольной Q*, потенциальной Q_ni и диссипативной Q_ai составляющих:

Подставим значение Q_t в уравнение (4.79), опуская индекс (*) при составляющей Q*:

Обобщенная сила Q_t, фигурирующая в этом уравнении, определяется с учетом работы источников всех внешних воздействий, а также некоторых внутренних источников, которые не могут быть отнесены к упругим и диссипативным элементам (например, силы кулоновского трения в механических системах).

Математическая модель, получаемая на основе уравнений Лагранжа второго рода, представляет собой систему обыкновенных дифференциальных уравнений вида

В эту систему входит п дифференциальных уравнений второго порядка, где п — число степеней свободы системы.

Процедура получения математической модели на основе уравнений Лагранжа второго рода включает следующие операции:

1) составление динамической модели технического объекта (при этом выделяются инерционные, упругие, диссипативные, трансформаторные и фрикционные элементы, определяются источники внешних воздействий);
2) определение возможных перемещений элементов системы с учетом наложенных позиционных голономных связей и введение обобщенных координат q_h количество которых должно соответствовать числу степеней свободы системы п;
3) составление выражений для вычисления кинетической Е_к и потенциальной Е_п энергий и диссипативной функции Ф Рэлея;
4) составление выражения для вычисления виртуальной работы 8W источников внешних воздействий, определение обобщенных сил Q*;
5) выполнение операций дифференцирования, предусмотренных уравнением (4.85), и формирование системы обыкновенных дифференциальных уравнений.

Отметим важное свойство функций Е_к, Е_п и Ф — их аддитивность. Напомним, что способностью накапливать кинетическую энергию обладают инерционные элементы, а потенциальную энергию — упругие элементы. Диссипативные элементы рассеивают энергию системы, затрачивая ее на преодоление внутренних сопротивлений. В связи со свойством аддитивности кинетическая энергия системы равна сумме кинетических энергий всех инерционных элементов. Потенциальная энергия системы равна сумме потенциальных энергий всех упругих элементов, а диссипативная функция — сумме энергий потерь всех диссипативных элементов.

В общем случае, когда состояния дискретных элементов системы, обладающих инерционными свойствами и взаимодействующих между собой посредством безынерционных упругих и диссипативных элементов, описываются несколькими обобщенными координатами, функции Е_к, Е_п и Ф для каждого элемента определяются по формулам (4.81)-(4.83). Примером такого объекта является твердое тело с шестью степенями свободы. Однако при моделировании часто встречаются более простые динамические модели, в которых состояние каждого дискретного элемента характеризуется одной или двумя обобщенными координатами. Тогда функции Е_к, Е_п и Ф значительно упрощаются.

Например, при плоском движении твердого тела кинетическая энергия равна сумме кинетических энергий в переносном (поступательном) и относительном (вращательном) движениях:

где т — масса твердого тела; v — скорость центра масс тела; J — момент инерции твердого тела относительно оси, проходящей через центр масс; ю — угловая скорость вращения тела относительно этой оси.

Кинетическая энергия сосредоточенной массы жидкости в дискретном элементе — участке трубопровода

где т_г — коэффициент массы, кг/м 4 ; Q — расход, м 3 /с.

Кинетическая энергия дискретного инерционного элемента твердого тела при одномерной теплопередаче

где с_т — теплоемкость инерционного элемента, Дж/К; Т — температура элемента, К.

Следует отметить, что Е_к в тепловой системе характеризует приращение кинетической энергии при нагреве на 1 К.

Кинетическая энергия инерционного элемента электрической системы

где L — индуктивность инерционного элемента, Гн; I — сила тока, А. Потенциальная энергия упругого элемента

где с — параметр упругого элемента (характеризует его способность накапливать потенциальную энергию — см. табл. 3.3); A-qi

Рис. 4.17. Динамическая модель трансмиссии автомобиля

Коэффициенты жесткости с₂, с₃, с₄ отображают упругие свойства карданной передачи, полуосей и шин соответственно, причем с₃ учитывает суммарную жесткость обеих полуосей — левой и правой. Диссипативные элементы с параметрами |i, расположены параллельно упругим элементам (на рис. 4.17 не показаны). Для отображения физических свойств сцепления трансмиссии и сцепления ведущих колес автомобиля с дорогой предусмотрены фрикционные элементы ФЭ₄ и ФЭ₂. Преобразующие свойства коробки передач отображены трансформаторным элементом T9j, а главной передачи — ТЭ₂. Внешние воздействия на систему: М_в1 — вращающий момент двигателя; М_в2 — момент сопротивления качению ведущих колес; М_в3 — момент сопротивления движению автомобиля (учитывает сопротивление качению ведомых колес, продольного уклона дороги и воздуха). Моменты М_тр1 и М_тр2 отображают реакции неидеальных связей, осуществляемых трансформаторными элементами ТЭ₄ и ТЭ₂, и позволяют учесть потери на трение в них. Моменты трения М_ф1, М_ф2 фрикционных элементов ФЭ₄, ФЭ₂ в процессе их скольжения (буксования) также представляют собой реакции неидеальных связей. Следовательно, моделируемая система неконсервативная. Поэтому при определении виртуальной работы 8ТК необходимо учитывать не только источники внешних воздействий М_в1, М_в2, М_в3, но и моменты трения М_тр1, М_тр2, М_ф1, Мф₂ зубчатых передач и фрикционов, несмотря на то что это внутренние потенциалы системы.

Получим вначале уравнения в предположении, что оба фрикционных элемента замкнуты, т.е. сцепление трансмиссии включено, а ведущие колеса не проскальзывают относительно поверхности дороги (качение без скольжения). В качестве независимых обобщенных координат выберем углы поворота сосредоточенных масс ф₂, ф₃, ф₄, ф₅, ф₆, ф₈. Зависимые координаты ф! = ф₂; ф₇ = ф_б.

Составим выражения для определения кинетической и потенциальной энергий системы и диссипативной функции.

где C0j — угловые скорости сосредоточенных масс.

Выражая угловые скорости масс через независимые обобщенные скорости, получаем

Потенциальная энергия

Составим формулы для определения деформаций Дф, упругих элементов, выражая их через независимые обобщенные координаты:

С учетом этих выражений потенциальная энергия

Так как диссипативные элементы динамической модели расположены параллельно упругим, то выражение диссипативной функции Ф имеет такую же структуру, как и Е_п:

Виртуальная работа источников внешних воздействий и реакций неидеальных связей при замкнутых фрикционных элементах и ФЭ₂, выраженная через вариации обобщенных координат,

Моменты трения в зубчатых передачах трансмиссии можно определить по формулам

где T)i, г₂ — КПД коробки передач и главной передачи; М_у1, М_д1, М_у2, М_д2 — моменты соответствующих упругих и диссипативных элементов:

Используя выражения для 8W, определим по формуле (4.80) обобщенные силы Подставляя в уравнения Лагранжа (4.85) составленные выражения для Е_к, Е_п, Ф, получаем следующую систему дифференциальных уравнений:

При буксовании сцепления ФЭ₄ число степеней свободы системы возрастает на единицу и возникает необходимость введения еще одной независимой обобщенной координаты ф₄. На движение элементов при этом оказывает влияние момент трения сцепления М_ф1, что учитывается при определении виртуальной работы реакций неидеальных связей:

где sign(co₁ — со₂) — дискретная функция, зависящая от знака аргумента (coj — со₂): при отрицательном аргументе она равна-1, а при положительном равна 1 (ее также называют функцией знака).

Необходимость введения функции sign обусловлена тем, что момент трения сцепления направлен противоположно относительной угловой скорости скольжения фрикционных элементов. При переключениях передач в трансмиссии угловые скорости сох и со₂ изменяются в широких пределах, а их разность может быть как положительной, так и отрицательной.

При буксовании сцепления ФЭх в математической модели изменяется только первое уравнение и вводится одно дополнительное уравнение:

Использование разных моделей для замкнутого и разомкнутого состояний сцепления создает неудобство при моделировании. Однако этого можно избежать и получить единую систему дифференциальных уравнений, учитывающую максимально возможное число степеней свободы моделируемого объекта.

Введем дискретные функции замыкания и размыкания сцеплений. Дискретная функция замыкания сцепления ФЭх имеет следующий вид:

где Дсщ — допустимая разность между сщ и со₂, определяющая условие замыкания.

При Дсох ₍]_H— — угловая скорость относительного скольжения поверхностей трения: для ФЭ! СОф! = (Ох — С0₂; ДЛЯ ФЭ₂ С0_ф2 = CDg — СО7.

На рис. 4.18 приведены графики, полученные при моделировании процесса трога- ния с места автомобиля массой т_я = 14950 кг на дороге, характеризуемой параметрами: / = 0,02; h =0,05; ф_хст =0,5; ф_хд =0,35;k_e =1,0. Параметры автомобиля: =3,6; J₂ =0,2; J₃ =2,573; J₄ =2,403; J₅ = 15,016; J₆ =91,318; J₇ =3777,5; J₈ = 15,0(J, в кг • м 2 ); q=21 300; c₂=73 870; c₃ =324 420; c₄ =696 900; c₅ = 187 500 (с, в Н м/рад); ^=5,26; ?^=6,59; a₃=4,26; r|!=0,96; r|₂ =0,95; r|₃ =1,0; M_P= 600 Н м; to_P = 220 рад/с; Мф1 щах = 1410 H • м; tv =0,7 c; r_K =0,5 m; L-3,95 м; =2,633 м; /г_с=1,35 м. Коэффициенты характеристик двигателя (4.68) и (4.77): Ь₀ =0,44; Ь₄ =1,87; Ь₂ =-1,31; k_p =4,0Нм- (об/мин) -1 .

Рис. 4.18. Графики переходного процесса при трогании автомобиля с места: а — угловые скорости сосредоточенных масс; б — угловые ускорения; в — моменты двигателя, сцепления, коробки передач и карданной передачи; г — мощности и работы буксования сцеплений; д — моменты сцепления колес, карданной передачи и полуосей

При определении параметров диссипативных элементов р,- использована формула (3.53). Выбор значений у_у осуществлен по рекомендациям работы [2].

В начальный момент времени при t = 0 угловая скорость вала двигателя со₁₀ = 167 рад/с, а скорость автомобиля равна нулю, поэтому со₂о = (Обо = 6)70 =0(рис. 4.18, а). При включении сцепления OBj нарастающий момент трения М_ф1 приводит к быстрому увеличению моментов М_у1, М_у2, М_у3 упругих элементов трансмиссии (рис. 4.18, в и д), автомобиль трогается с места и начинает разгоняться, угловая скорость массы J₇ возрастает (рис. 4.18, а). В конце процесса буксования сцепления угловая скорость со₂ его ведомой части быстро возрастает и сцепление замыкается. Но при этом момент превышает момент трения сцепления ведущих колес с дорогой М_ф2 (рис. 4.18, д), вследствие чего колеса проскальзывают относительно дороги (сое > со₇ — на рис. 4.18, а). Проскальзывание колес сопровождается многократными пиковыми значениями моментов в упругих элементах, создающими повышенную динамическую нагруженность механизмов трансмиссии и снижающими их долговечность. Графики работы трения и мощности буксования сцепления трансмиссии W_cj,i, Р_фi и колес автомобиля 1Г_ф2, Рф2 представлены на рис. 4.18, г.

Видео:Уравнения Лагранжа второго родаСкачать

Уравнение Лангранжа второго рода

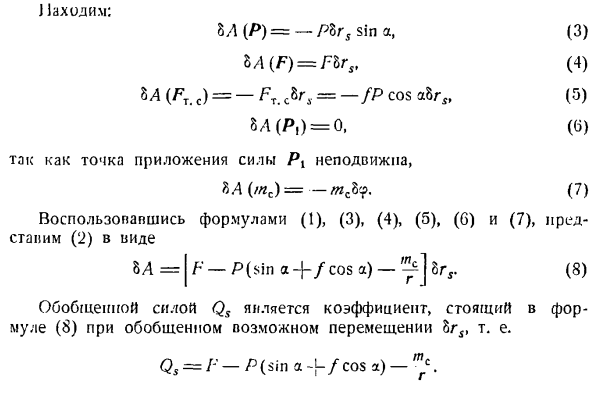
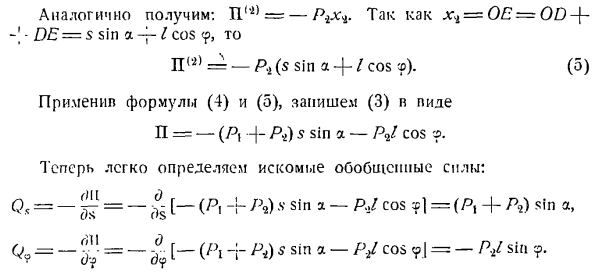
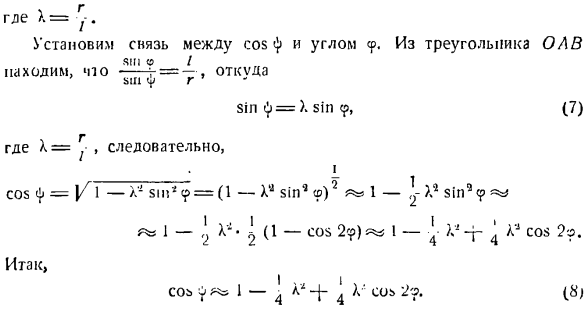
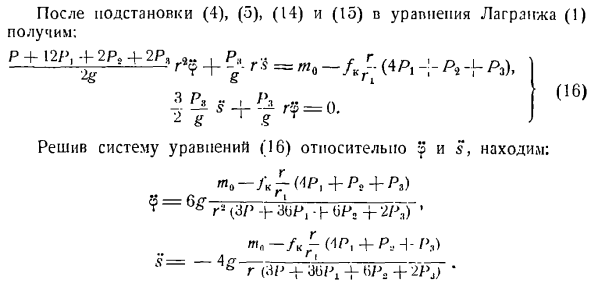
Видео:Дифференциальное уравнение Лагранжа II рода. Расчет механической системы.Скачать

Уравнение Лангранжа второго рода

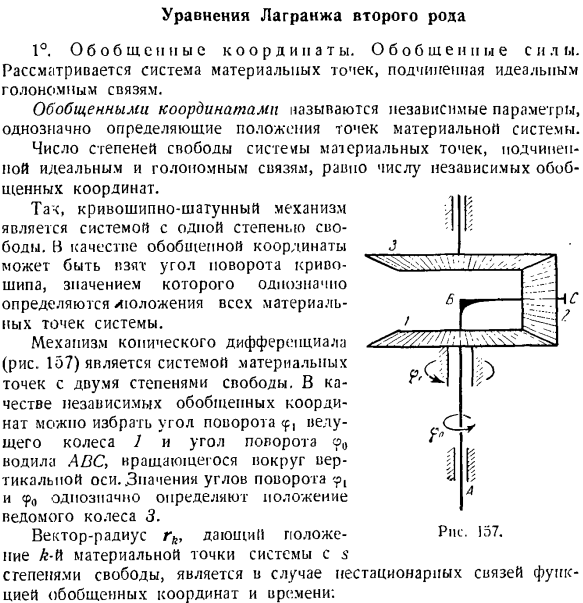
Уравнение Лагранжа типа 2 1°.Обобщенная координата. Обобщенная сила. Рассмотрим систему материальных точек, подчиненных идеальной голономной связи. Обобщенные координаты-это независимые параметры, однозначно определяющие расположение точек материальной системы. Число степеней свободы в системе масс, подчиненных идеальным и голономным отношениям, будет равно числу независимых обобщенных координат. Механизм касания

и рукоятки система с 1 степенью freedom. As обобщенные координаты можно принять за угол поворота кривошипа, величина которого однозначно определяет расположение всех важных точек системы. Механизм дифференцирования конуса (рис. 157) представляет собой систему материальных точек с 2 степенями freedom. As независимая обобщенная координата, вы можете выбрать угол поворота

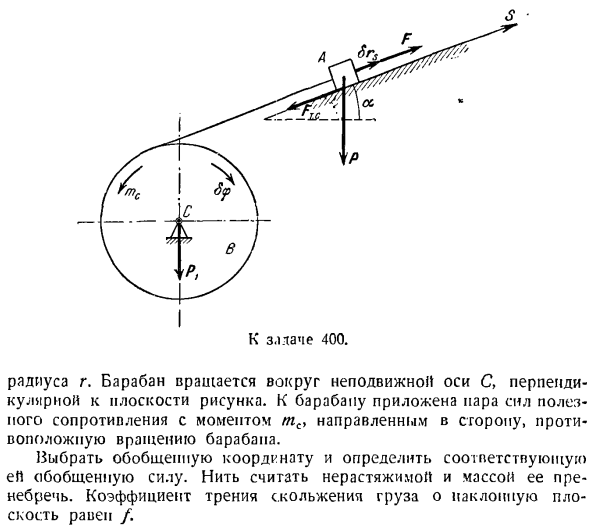
Полезная сила сопротивления приложена к барабану, с моментом направленным в противоположное направление к вращению барабанчика. Людмила Фирмаль

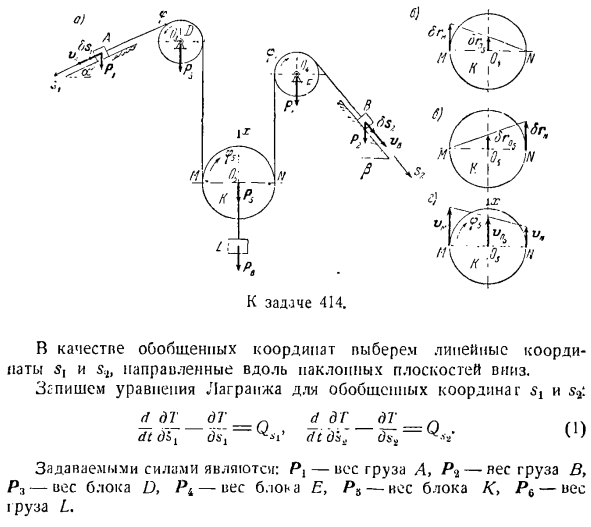
3. Радиус-вектор hl дает положение N-й материальной точки системы со степенями свободы, но в случае нестационарных соотношений он является функцией обобщенных координат и времени. И Да. О Рисунок 157. 400 к несчастью. Радиус города: барабан вращается вокруг неподвижной оси С, которая перпендикулярна плоскости рисунка. Выберите обобщенные координаты и определите соответствующие обобщенные силы. Нити считаются

расширяемыми, а их масса игнорируется. Коэффициент трения скольжения груза по наклонной плоскости равен/. Поэтому уравнения движения для целевой системы были составлены с использованием уравнений общей динамики в задаче 396 и 2 методов использования уравнений Лагрейджа в этой задаче. Сравнение двух приведенных методов показывает преимущества использования уравнения Лагранжа. Решите задачу n используя

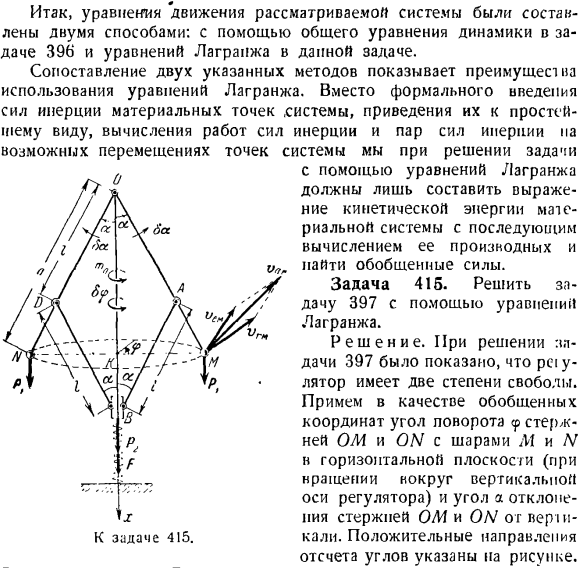
уравнение Лагранжа вместо формального введения сил инерции материальных точек системы и приведения их к простейшему виду и вычисления работы пары сил инерции относительно возможного смещения точек системы Необходимо найти обобщенную силу, составляющую лишь выражение кинетической энергии материальной системы и последующий расчет ее дифференциала. Задача 415.Решите задачу 397, используя уравнение Лагранжа. Solution. In решая задачу 397, было показано, что U-излучатель pci имеет 2 степени freedom. As обобщенные координаты, принимают угол a ом и на-стержне

а угол a ом и на-стержне Людмила Фирмаль

(2). Форекс-2С /(1-соз а). (2） Дадим контроллеру общее возможное смещение Sep и Sa, направленное на соответствующее увеличение угла поворота. Чтобы вычислить обобщенную силу, 8A возможно смещение, предполагая ноль, 8? ^ 0,8 а = 0. Это означает, что если угол a, образованный вертикальным стержнем OM и ON, постоянен, то регулятор получил угловое смещение 8

вычисления обобщенной силы Qa зададим регулятору возможное смещение 8a, учитывая, что возможное смещение 8

Знак минус указывает на то, что возможное движение муфты B вверх, если sin равно 8. Вычислить сумму работы заданной силы на возможном пересечении точек системы, соответствующей обобщенному возможному сдвигу 8а. В (5） (6） 8л = — 2л, sina5a-Джей-Р28лг0 + Fxbx (Коэффициент 2 в первом члене обусловлен тем, что регулятор имеет 2 шара.) Подставляя значения Lpn и Fx из формул(4)и(2), получаем: ба = — u-коэффициент абсолютной скорости для каждого из шаров M и N. каждый шар участвует в сложном движении. Угловая скорость φ-это вращение вокруг вертикальной оси регулятора, а относительное вращение вокруг горизонтальной оси O, перпендикулярной плоскости фигуры, — это угловая скорость 4.Примените теорему сложения

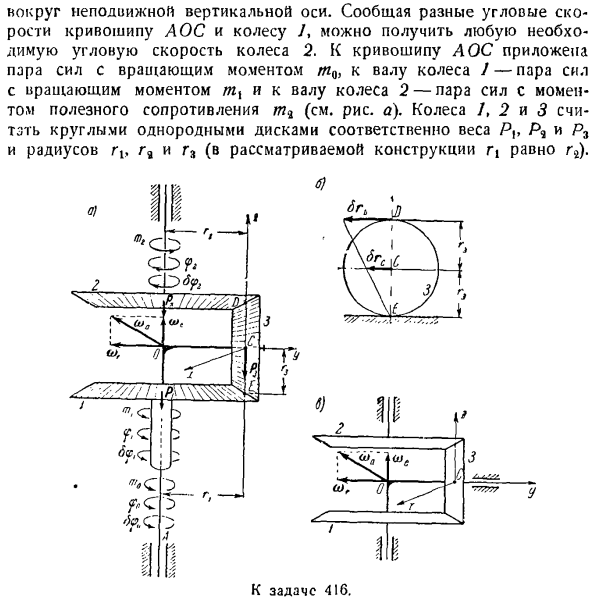
скоростей точек： МВС = = 4 J(10） возьмите производную по времени от координаты xn связи B относительно угла поворота d, чтобы определить проективное значение х + ^ + / ЗР (0 ′ −2–2 ВТ ДОЛГОТЫ、 Где©c-скорость центра тяжести колеса wv、 Абсолютная угловая скорость o) подвижные координатные оси x, y, g на колесах 3 a, 13x, / Lu, / Lg-осевой момент инерции,/ 3, x, / Zx-центробежный момент инерции Колесо меньше

5 для соответствующих осей. Выберите начало координат оси центроида колеса 3 C. укажите вертикальную ось g горизонтально вправо вдоль относительной оси колеса 3, а ось y, а следовательно, и ось x, перпендикулярно плоскости рисунка. При аналогичном расположении координатных осей легко заметить, что они являются главной осью инерции колеса 3(колесо 3, а также колесо/и 2, считаются однородными круговыми дисками).Результат、 = / ^. = 0, и формула для расчета кинетической энергии колеса 3 т [’л) упрощается. 7″ » =1А^ +1 (/«ш+/, v, 0j.(9） для расчета wv, shu

необходимо определить абсолютную угловую скорость колеса 3.Колесо участвует в переносных вращательных движениях угловой скорости вокруг вертикальной оси и относительных вращательных движениях вокруг оси симметрии колеса 3. давайте представим наблюдателя в провернуть операционной системы, чтобы определить, Вт. Для этого наблюдателя, этот чудик, кажется, не двигаться. Как следствие, относительную картину движения представляется глазу наблюдателя. Колеса/, 2 и 3, по-видимому, вращаются вокруг неподвижной оси(см. Рисунок C).Напишите зависимость между относительной угловой скоростью колеса и радиусом. Ин ый> Ин гл» Где ω, ω’.)) обозначает угловую скорость

колес/, 2 и 3 относительно кривошипа, вращающегося с угловой скоростью ω0.Однако 2-я дробь имеет знак минус, и если учесть пропорции вместе, то необходимо указать разные направления движения колеса/и относительную угловую скорость движения колеса/. 2.In факт、 Мл.） если бы непев жил в другом месте, то это было бы: — =- Условия r. 2 = для r1, a>(f> = = — CC) = = co0, а для coco1-ω0, o).2 =2ш0-ω, то есть =(Ю） Из первой дроби определите относительную угловую скорость»•/ » колеса 3： / «(| Гг)= т«(о).2-О)

0）、 ч’3 Возмещение (?.- ? «) •(Р） Р Направление масла указывается кружевом. е. Для добавления жесткого вращения вокруг пересекающихся осей применим icopevy к колесу 3: ioa — e + o > r(см. Рисунок? это не. Теперь нетрудно вычислить проекцию абсолютной угловой скорости G).x), колесо 3 па на оси y-z, плотно соединенное с ним. 0, Ву = — си/’, — со*). Принимая во внимание формулу (11) и отмечая ее=φ0, получим: о) = 0,о>>, =—(ти — > о ^ = Введем эти значения 0 и φ и получают производную полученного результата по времени. Мы это выясним： я£= + + + /—））»-（2 /、+ liy-r±) — ЗУ

—)7г » y3g- 2г 1 ^ г> ’Б-2г’ 4г ’ Уравнение движения дифференциала (17) принимает вид: (18） ^ [8П р?, Л = п— 2М з = мл + Ми. Используя формулу(10), вы получаете следующую формулу:$ 9 = 2?0 — подставив n в это выражение, получим искомое угловое ускорение колеса 2. .. _ _N (2L-M)+ 5(2L1- Р. Г1 Здесь Ku L1U IV D S имеет значение, описанное выше.

Решение этой задачи с помощью теоремы общей динамики сопровождается большими трудностями. Применение уравнения Лагранжа позволяет относительно легко получать дифференциальные уравнения движения, и опять же удобство применения уравнения Лагранжа при решении сложных задач динамики систем с несколькими степенями свободы.

] 1алодим： Л (/>)= — Pbr5 грех, (3） Л (Ф)= Связанные С FBR, (4） БА (м с)= — фут. с8га. = — /П, потому что АБР (5） М(П)=0.（(5), поскольку в точке действия силы P является фиксированной、 БА (МС)= — МЦБ = п — Зин Ин.(8） Потенциальная энергия весовой силы Р (4) равна пуле. N » 2> =0.(9 )） Потенциальная энергия. P13; сила упругости пружины F равна P(3)= 2.Если подставить значение выражения (2)、 =РР *(1-а°) 2. (10 )） Используя выражения (8), (9) и (10), запишите выражение (2) в следующем виде: = = P, sino -> — для R ’ 2(1-cos?2). (И） Для вычисления обобщенной силы объекта, обобщенная координата

В9 =—[РХ с COS в 09 =

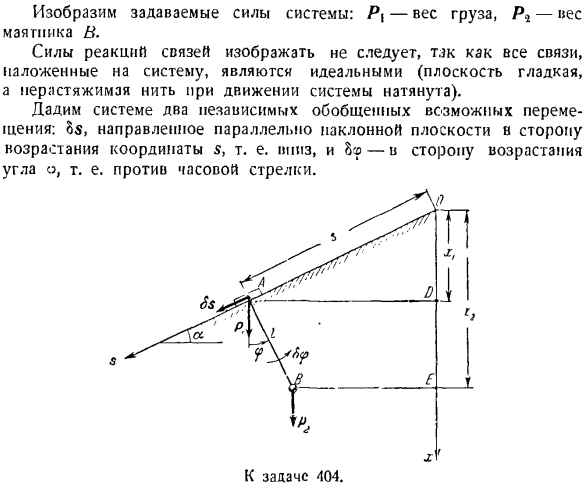
、 К М(ф)= + БГС(б） Примените Формулы(3), (4), (o) и (G)для описания (2) в виде: +(7） Обобщенная сила Q является коэффициентом пропорциональности формулы OG (7). Р Проблема 404.Груз а перемещается по гладкой наклонной плоскости угла а относительно горизонтальной плоскости. Маятник веса прикреплен к грузу A. длина строки маятника/. 」 Выберите обобщенные

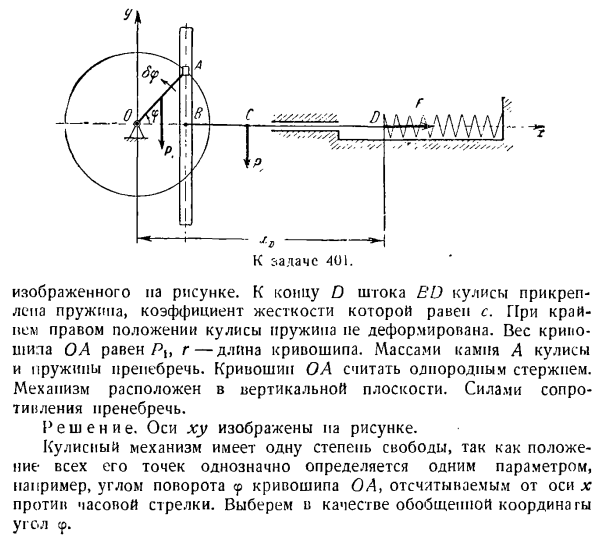
ие. Поскольку для определения местоположения массы необходимо задать 2 независимых параметра, рассматриваемая система имеет 2 степени свободы. 1. один параметр определяет положение груза A на наклонной плоскости, а второй параметр определяет положение математического маятника B относительно груза A. Возьмите начало отсчета O случайным образом и направьте ось s вниз по склону. От точки O, точка вниз по оси x вертикально. Угол, под которым маятниковые нити перпендикулярны, обозначается

этой материальной системы: 5 и 9.В соответствии с этими обобщенными координатами существуют 2 обобщенные силы: Qs и Qr Показывает силу установки системы. Px-вес груза, P4-вес маятника B. Она не должна показывать силу реакции сцепления, так как все соединения, приложенные к системе, идеальны(когда система движется, плоскость становится гладкой, а вытянутые нити растягиваются). Дает системе 2 независимых обобщенных возможных перемещения. В формуле определения возможных перемещений БРК

обращает внимание читателя на то, что 1 член меньше формулы ® ). (5） Примените Формулы (4) и (5), затем напишите (3) и pide. П=-(Р,• -) — P4) 5 sin a-Р2 / cos теперь вы можете легко определить желаемую обобщенную силу. М,= — Г = — ^ [- (Р, — ’ РФ) с грех-Р, / Кос =(П+ а) грех、 В9 = — Ф = — у [- (РІ-Р М) ООО 《. — Пи Джей, Кос? / =- м / СР грех. Решая следующую задачу, мы можем объяснить обоснованность применения этого метода расчета обобщенных сил в случае систем с несколькими степенями свободы, в которых существуют только потенциальные заданные силы. Задача

405.Установите 3 диска в герметичный горизонтальный эластичный вал на одном конце ступени. Если центр тяжести диска находится на геометрической оси вращения, выберите обобщенные координаты и определите соответствующие обобщенные силы. Модуль упругости вала равен S. Решение. В этой системе есть 3 степени свободы. Указывает угол поворота диска, соответственно.9, cp9 и

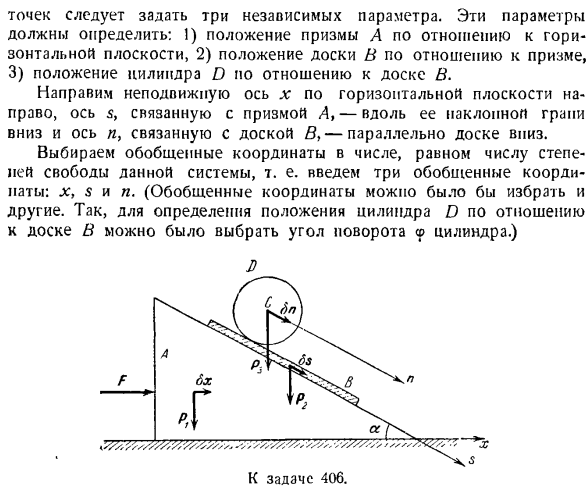
социальная природа Формулы (1) bx-это обобщенная сила Qx. QX = R Предположим, что 8sΦ0 и bx = = op = 0 определяют обобщенную силу Qs. Это означает, что цилиндр неподвижен относительно призмы и платы относительно горизонтальной плоскости. Только плата, соединенная с цилиндром, движется вниз по боковой наклонной плоскости призмы 8s. Например, сумма работы всех сил, приведенных с возможным смещением в 8 секунд, записывается в виде 8 A = ( / > , + / > a) 8-секундный грех a. (2） Действие сил F и Px равно действию пули. Смысл действия этих сил в том, что они не движутся. Обобщенная сила Qs — это коэффициент,

представляющий собой 2s формулы (8). М,= (/Ви〜П3) грех. Переходим к расчету обобщенной силы Qn. So будем считать bnΦ0, bx = b $ = 0. Это означает, что призма неподвижна относительно призмы и горизонтальной плоскости, а поскольку душ перемещается относительно доски, его центроид C перемещается вниз вдоль оси n до 8l. Рассчитайте величину работы заданной силы на возможное перемещение Ln. БА = P38l грех. (3） Сила F, P и P. 2 задания равны нулю. Потому что точки действия этих сил не двигаются. Обобщенная сила Qn-это коэффициент, который находится в cn в уравнении(3). Дя = Пт греха я. Поэтому необходимая обобщенная сила имеет

следующий смысл: Ц = ф, Qв =(Р9-п-Р3) грех,= А. грех 2 обобщенное уравнение динамики в обобщенных координатах.2-й вид уравнения Лагранжа. Общая формула динамики системы масс н Х(ФК-mbwk).СРК = 0 к»■я В обобщенных координатах существует форма. [д ДТ N, д / д ДТ от N ,. 。 * / д ДТ от Где Q гв. QS является обобщенной координаты, КЖ> дь QS является обобщенной скоростью, и hqb непосредственного обращения обобщен Смещение системы-это

изменение соответствующих обобщенных координат Q, Q. lfQs-обобщенная сила системы, T-кинетическая энергия системы. Для систем, подчиненных полому насосу, bqy, 8q. поскольку 2i bqs является независимым обобщаемым перемещением, общее уравнение динамики удовлетворяется только условием, что коэффициент, находящийся в возможном перемещении, равен пуле. д ДТ _ ДТ _ ДТ Н йй dqt-КЖ> dT_dT_n д ДТ Д d dT dT_ да d’Ant C dq3 Ws * д ДТ dT = _dP ДТ б ’ д ы в DQS DQS с ’ * ) Такого рода уравнение Лагранжа класса 1 не рассматривается. Таким образом, приведенное ниже уравнение Лагранжа типа 2 называется просто уравнением Лагранжа. Вводя Лагранжеву функцию Lt, равную разности кинетической

и потенциальной энергий, для L = T — P уравнение (2) принимает вид: д 0L » dl_ » в ^ Йй DQL по

’ (3 *） д дл _ дл n ДТ йй, ’dq3 ’ д дл дл _ г ДТ служб DQS DQS с Трудность решения задачи динамики системы материальных точек с 1 степенью свободы заключается, в частности, в успешном выборе соответствующей общей теоремы динамики. Для систем с некоторыми степенями свободы решение задачи значительно сложнее, так как решение задачи требует совместного применения общей теоремы и других кинематических relations. In в таких случаях наиболее удобно использовать уравнение Лагранжа. Уравнение Лагранжа является универсальным методом

для составления дифференциальных уравнений движения материальной точечной системы. Большое преимущество уравнения Лагранжа состоит в том, что при наличии идеальной голономной связи сила реакции связи не учитывается. (При применении других методов решения задачи сила реакции связи должна быть исключена из системы составляющих уравнений при решении задачи.）

Динамика системы уравнений, полученная выше при решении большинства задач, может быть выведена непосредственно с помощью уравнения Лагранжа. В зависимости от условия задачи, когда необходимо найти реакцию связи, уравнение Лагранжа используется для определения точки ускорения системы, применяя принцип освобождения связи к соответствующей массе системы и используя либо теорему общей динамики, либо метод

кинетической статики. При решении задач в динамике, когда нет четкого плана применения тех или иных теорем, необходимо отказаться от использования уравнения Лагранжа. Все вышесказанное не умаляет важности теоремы в целом. Общие теоремы рекомендуется использовать при решении некоторых простых задач динамики (см. главу XI ниже). Составление уравнения Лагранжа следует проводить в следующем порядке: I) определяет число степеней свободы в материальной системе. ’> ) Выберите систему координат и введите число независимых обобщенных координат, равное числу степеней свободы. 3) определяет

обобщенные силы Q, Q, Qs системы, соответствующие выбранным обобщенным координатам. (Процедура расчета обобщенной силы подробно описана в пункте I настоящего раздела.) 4) вычислить кинетическую энергию t системы рассматриваемых материальных точек. 5) найти частные производные кинетической энергии в сумме 。。。 дециграмм Скорость 7) подставьте результаты, полученные в разделах 3, 5 и 6, в уравнение Лагранжа. Проблема 407.Уравнение Лагранжа используется для получения дифференциальных уравнений для вращения твердого тела вокруг неподвижной оси. Решение. Твердое тело, которое вращается вокруг неподвижной оси, имеет 1 градус freedom. In дело в том, что для определения местоположения всех точек достаточно задать

1 параметр, например, угол поворота

заданных при этом возможном смещении： 8-4 = 2 Сус 8? = [Тртп») J Я） к-1 к-я Обобщенная сила Q9 — это коэффициент, который находится в Формуле (2). Q,= X’M ^ a). (3） К 1 ноября. Кинетическая энергия твердого тела вращающегося вокруг неподвижной оси имеет следующий вид Вычислите частную производную кинетической энергии относительно обобщенной скорости ДТ, нет. А затем возьмите производную по времени от результата： д ДТ г Дж ДТ с = ’А — Заметим, что кинетическая энергия массы T не зависит от обобщенных координат x, y, z、 ДХ ды-б£ — (о> Формула（2）、（3）、（4）и (3) присваивается системе уравнений Лагр ГHkY> = X 17кг k = I k I fe ^ 1 Он от потенциальной энергии системы в соответствии с соответствующими обобщенными

координатами, т. е. dqi ’ Где r = 1,2,…、 Расчет обобщенных сил материальной системы является одним из ключевых этапов решения задачи с использованием 2-го уравнения Лагранжа. 1. Решение о обобщенной силе может быть осуществлено двумя способами: а)наиболее распространенным приемом является вычисление обобщенной силы в виде коэффициента, выражающего сумму основных действий данной силы и соответствующего обобщенного возможного displacements. In в этом случае расчет обобщенных сил следует проводить в следующем порядке: 1) исследуйте число степеней свободы в рассматриваемой системе масс и выберите

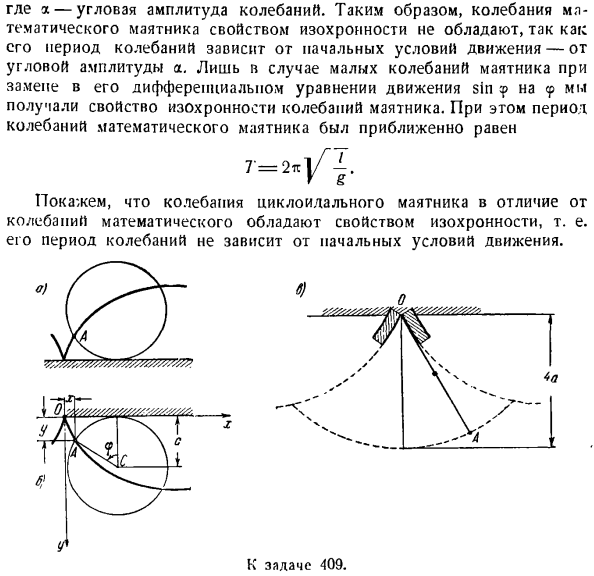
соответствующие обобщенные координаты. 2) показать всю настроенную мощность системы. 3)Если все связи, наложенные на материальную систему, не идеальны, добавьте к данной силе соответствующую реактивную силу связи (силу трения и т.). 4) число обобщенных координат, то есть равное числу степеней свободы в материальной системе, дающее системе независимое обобщенное возможное смещение. Проблема 409.It доказывается изохронизм колебаний циклоидального маятника. Решение. Маятник называется циклоидой и может быть отображен как материальная точка, которая движется по дуге окружности циклоиды. При решении задачи 284 учитывался математический маятник, в котором дуга является орбитой. Дифференциальный звук колебаний математического маятника, записанный в уравнении 284 (4)、 п + £ грех? = 0、 Где о-

угол отклонения маятниковой нити от вертикали, а/ — длина нити. В уравнении (II)той же задачи период колебаний математического маятника г = 2.: Ил(л + Tsinl 2 + элсинт 2-я -••••). Где а-угловая амплитуда колебаний. Таким образом, колебание математического маятника не имеет изохронных свойств, так как его колебательный период зависит от начального состояния движения, то есть от угловой амплитуды a. In в случае малых колебаний маятника, при замене sin дифференциальными уравнениями движения, только

In в этом случае периоды колебаний математического маятника примерно равны Колебания циклоидного маятника указывают на то, что они обладают свойством изохронности, в отличие от математических колебаний. К выпуску 409. Обычное представление о циклоиде связано с локусом точки А, которая находится на краю катящегося колеса без скольжения по рельсу прямой линии (см. рисунок а). Па рисунке б это колесо катится по рельсу на колесе без скольжения снизу. Движение точки А

является колебательным движением, что указывает на то, что ее колебательный период не зависит от начальных условий движения (конструкция циклоидного маятника обсуждается ниже). В качестве обобщенной координаты выберите угол

Единственной указанной силой является масса груза, обозначаемая R. Потенциальная энергия Р массы выражается формулой: Р = ру = — ра ([- а (3） Виде обобщенной силы QF-это скорострельный ЖП. Вводя Формулу (3) выражение в эту формулу: Qv = Pasin

Вычислите частную производную кинетической энергии 7 ’для обобщенной скорости φ. = 2 maq (1-cos и рост нагрузки Б Б. легко видеть, ’3 Поэтому 8R = — р38 (Λ(9） Кинетическая энергия системы T (p! ！- «•с」） Подставляя Формулы (3), (9) и (10) в уравнение Лагранжа (1), получаем дифференциальное уравнение движения лебедки для обобщенной координаты».. ’, / г. «О1） (Л + П. ^ + Л +Гротц В случае W: Pj-r^ ускорение груза B направлено вверх. в случае mQPiГ-ha ускорение нагрузки B направлено вниз. п0 = = Pk-ha, лебедка

остановлена, или вся масса движется Равномерно. Направление движения зависит от начальных условий движения. Эта задача также может быть решена с помощью дифференциальных уравнений для вращения твердых тел вокруг неподвижных осей. н / ?= 2 МЗ (ФК)> к = Это должно было быть составлено 2 раза.1 для шестерни, другое для остальной электрической ворота. Для Необходимо было мысленно разрушить эту систему в нижней части детали и зубчатой передачи/и 2 точках склеивания, заменив действие отброшенной части конструкции соответствующей реактивной силой сцепления. R, который составляет систему дифференциальных уравнений

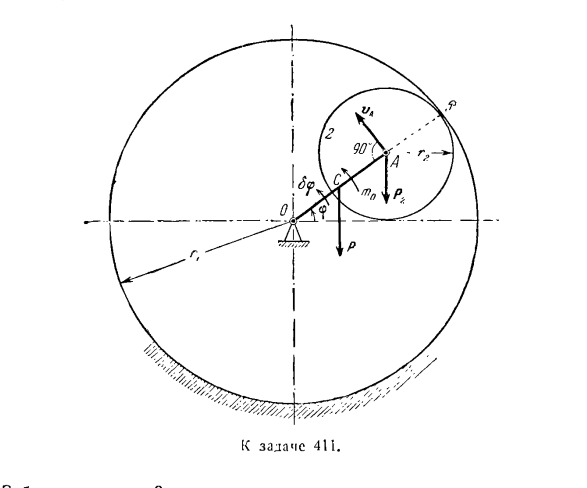
движения, включает в себя силу реакции сцепления. Только после исключения этой силы реакции из результирующей системы уравнений может быть достигнуто уравнение (11).Преимущества уравнения Лагранжа, не содержащего реакции связывания, очевидны. Задача 411.Определите угловое ускорение коленчатого вала в вертикальной плоскости. Шестерня 2 внутренне зацеплена с неподвижной шестерней/.Колесо 2 использует кривошип OA для перемещения гайки, и применяется силовая пара с крутящим моментом от// / 0 до v. Вес кривошипа OA равен P, вес колеса

2 равен g2, радиус колеса 2 равен радиусу неподвижного колеса L Колесо 2 считается однородным круговым диском, а кривошип O / H-влажным однородным стержнем. Игнорируйте сопротивление движению. Решение. Поскольку угол поворота кривошипа ОА определяет все положения, планетарная передача имеет 1 степень свободы. Механизм действия point. As в качестве обобщенной координаты выберите угол 9, измеренный либо по горизонтальной оси, либо против часовой стрелки. Уравнение Лагранжа обобщенных

координат-Р41 0.4 [Кост и R. 0Л= 0&> — — f(3） И затем…

Кинетическая энергия ползучести ОА, вращающейся вокруг неподвижной оси о, перпендикулярной плоскости фигуры, вычисляется по формуле= ^ — О-я-ОА ^ л-т ^ — СБР-момент инерции кривошипа. Так… (4 )） Кинетическая энергия шестерни 2, которая совершает плоское движение Найти скорость точки А, конечную точку кривошипа ОА. ба = ОА ч =(ГУ-б) х. (6） Рассмотрим скорость той же точки А, которая принадлежит шестерне 2, относительно мгновенного центра относительно скорости колеса. vA = a iP•u = r9sh2. (7 )） Если мы сравним формулы (b) и (7), то увидим следующее: г-г.

Два Момент инерции шестерни 2 рассчитывается по следующей формуле л (9) Если подставить выражения v5, coi и/ d из выражений (6), (8) и (9) соответственно, то выражение (5)будет иметь следующий вид: (У） Уравнения (3), (4) и (10) используются для описания уравнения кинетической энергии планетарного механизма. + *(ВТОРОЙ） Вычислите частную производную кинетической энергии t, но обобщенная скорость равна: dT 2P + NR、 СФ = — ЭИ -» -’»> -?В =(8)я• » А затем возьмите производную по времени от результата： Д ДГ ^ г + ОГ ^» Как- — — — (Т | Р потому выражение (9), ХС = rcos СР +(1–4 +1 х * соѕ 2? ）、 Иначе говоря = Ж + р так? + ’8′); 2 / cos Откуда ■ * С = — Р(грех 9-(—^- х Sin 29 ^ 9.(11） Центр тяжести кривошипа и шатуна ОА расположен на их средней точке и имеет такую же ординату в конструкции Нам = язык yct = 2-си » б Откуда —

’Р£соѕ (О.- Если ввести значение xc и усов из Формулы (10) в формулы (11) и (12), то вы увидите следующее: В * = РМ(грех 9 + т х Sin 2?V-Ч Т потому что * * 9 (13 )） Формула (G) для Формулы ma и формулы (P) и (13） П /- И. Учитывая то, что мы получаем： g»»: = с°с » С. От (21） Где/ pr определяется выражением

(18).Формула (21) представляет собой дифференциальное уравнение для движения кривошипно-шатунного механизма. Задача 399.Определить обобщенную силу в случае движения математического маятника массы р, Если длина нити равна/.Для обобщенных координат возьмем угол отклонения

При решении обратной задачи, то есть при определении движения заданной силой, часто используется численное интегрирование, так как решение дифференциального уравнения (21) затруднено. В зависимости от состояния задачи необходимо определить закон изменения крутящего момента M. Это позволяет получить равномерный кривошип Bpauienne, или cf. Далее, она равна 3 = 0, и решение уравнения (21) относительно m дает следующий результат: Куда? + Xsin 2?(С COS Так как кинетическая энергия material материальной системы, определяемая формулой (13), не зависит от обобщенных координат cp и S.、 ДТ ДГ л （4）、（5）、（14）、подставляя и(15)в уравнение Лагранжа(1), получаем: Р + 12Р,+ 2Р, м-2Р, Р.? +£Шя (4П | п, П3）、 (16） — ?■^§- Ф Р? = Приблизительно. 1.Е Р Решая одновременно уравнения (5 и S) (16), можно видеть: = r—H aor,-h (jp, −2 /> TG ’ (Inlex

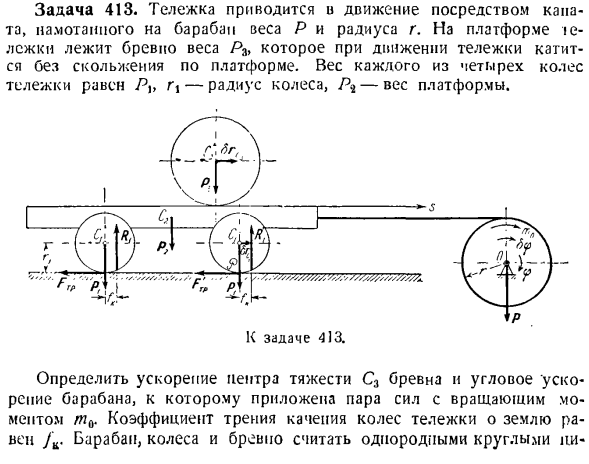
CP с обобщенной силой Q является координатой(ЛРН * — •3/л, — / — 2×3)^ ’о — / тр-н-б Р2 4 * па） o_9 а _ _ _ / 2 (При выводе этих уравнений предполагается, что/ = 0 a = s = 0.) Задача 414.Решите задачу 396, используя уравнение Лагранжа. Solution. In решая задачу 396, было показано, что рассматриваемая система имеет 2 степени свободы. В качестве обобщенной координаты возьмем линейную координату 5 |傾斜面に沿って下方に向けられたs. lt запишите уравнение Лагранжа для обобщенных координат S.< ±dT_dT_p Д ДГ г dtdli 3s] — Дидди; Ди、〜 Заранее поставленная сила:Т 7 Рг2 10 = — так、 Кинетическая энергия постепенно движущейся платформы принимает форму −2 г в•

Учитывая, что, учитывая нерасширяемость веревки a=, вы можете увидеть следующее: =(8） Колесо вагонетки сделает квартиру motion. So … R G Если момент инерции колеса равен/, = вращать — Я ЗГ. виртуальный канал Без проскальзывания vr = 5.Резьбовой стержень Ы ы ы ы Тельпо. J [если подставить значение этого vc в выражение (I)、 744)= 1.&r V + J ^ + £ (, 2） (6) Формула（7）、（8）、（9）и (12) к/(1), 7 ’(i T TG ’ (Inlex CP с обобщенной силой Q является координатой(ЛРН * — •3/л, — / — 2×3)^ ’о — / тр-н-б Р2 4 * па） o_9 а _ _ _ / 2 (При выводе этих уравнений

предполагается, что/ = 0 a = s = 0.) Задача 414.Решите задачу 396, используя уравнение Лагранжа. Solution. In решая задачу 396, было показано, что рассматриваемая система имеет 2 степени свободы. В качестве обобщенной координаты возьмем линейную координату 5 |傾斜面に沿って下方に向けられたs. lt запишите уравнение Лагранжа для обобщенных координат S.< ±dT_dT_p Д ДГ г dtdli 3s] — Дидди; Ди、〜 Заранее поставленная сила:

Все соединения, наложенные на систему, идеальны (так как наклонная плоскость должна быть идеально гладкой, на оси блока нет трения, а нити не растягиваются и не растягиваются). Для определения обобщенных сил QH и Q $ 2 приведем нагрузки A и B, соответственно, возможные перемещения SSj и направление, направленное параллельно линии максимального наклона наклонной плоскости в направлении увеличения координаты s.、％ Чтобы вычислить обобщенную силу QS, мы даем системе обобщенное возможное смещение Ss, предполагая, что [lsq равен нулю. Φ0,=(это

возможно, потому что » и ’ в являются независимыми обобщенными координатами.） Поэтому правая ветвь потока от нагрузки B, блока E и нагрузки B до точки N останавливается. Точка м нити получает вертикальное восходящее возможное движение Lm, размер которого равен Ss, поскольку нагрузка а может перемещаться вниз из-за отсутствия удлинения нити. Определите возможное смещение оси блока Sr0, принимая во внимание, что точка/ V нити накала остается в покое в то же время (см. Рисунок B).Это равно половине модуля модульно-способного перемещения 8gL1, то есть Ох 2.2 * Ж Рассчитайте сумму работы сил, приведенных к обобщенным

8 секундам, возможное перемещение точек системы, соответствующее возможному перемещению груза А. (В БА = РХ грех aZsi-(РВ + П6) б Рассматривая Формулу(2), можно увидеть: ал = [Р, грех-я(/> т + /> я)] та. (3） Гравитационная работа п. 2 равна пулевой, т. к.= 0, поэтому работы гравитации Р3 и Р4 равны нулю, т. к. точки приложения этих сил не перемещаются. Обобщенная сила QS1-это коэффициент, который находится в обобщенном возможном смещении уравнения (3). Под рукой-грех-у(П5 + П6). (Ля） Чтобы вычислить обобщенную силу Q $ 2, Дайте системе обобщенное возможное смещение Is, предполагая, что ОС равна пуле. Это

означает, что блок D груза а и левая ветвь нити а груза а находятся в точке М нити. Из-за нерастяжительного характера винта, из-за возможного перемещения нагрузки на ПА, точка N винта Излучает возможное смещение L ^вверх в вертикальном направлении. Это считается смещением и С. 3. размер равен модулю упругости. Учитывая, что точка нити M неподвижна в то же время, она выглядит так (см. Рисунок C） ^ О3 = =(5） Обобщенные возможные перемещения вычисляют сумму работы заданных сил на возможные перемещения точек системы, соответствующих ос4： BA = P,^ sin ft — (Pe + Pb) если рассматривать уравнение (5)、 БА = [Р4 грех? -я (П8-Ф Р6)] СУ4. (си） Работа гравитации Pt равна нулю, потому что s = 0.Работа

гравитации P3 и P4 равна нулю, так как их точки приложения неподвижны. Обобщенная сила QSi является коэффициентом в уравнении (6) os4. Вопрос, с = P4sin?^ Я(ЧП + П6). (7 )） Переходим к расчету кинетической энергии t материальной системы, состоящей из 6 масс: блоков D, E, K, A, B, L： м = ро ОКБ) 7(ч) Пи)пн _ [_ ППГ(г） Скорости нагрузки A и 8 fl направлены параллельно линиям максимального наклона наклонной плоскости. Проекция этих скоростей на ось s будет равна sx и s соответственно.2. Радиус блока D, E, K обозначается через r3, r4 и guard. In в этом случае угловые

скорости блоков O и E выражаются следующим образом: (9 )） Из-за не масштабируемости нити скорость Vm точки нити M равна скорости vA груза A. R>Λ1¥=£,.Аналогично: v / Wx = 9. использование рисунка очень просто. g, найти скорость движения оси Ov блока K>do plane motion： (10 )） Девять в Два Два Чтобы определить угловую скорость блока K, найдите скорость точки M и получите точку / V полюсов. Иначе говоря (vMN) x = 1 MN = 2rv£6, 2r3 ’?3 = .поскольку это v, угловая скорость блока равна K’. Кинетическая энергия груза а и в、 = 1 5. .В.], (П2） Рассчитайте кинетическую энергию блоков D

и E, которые вращаются вокруг неподвижной оси. Т© — 1 / А2 Т — я СВ2 1-2 пр™ » = 2 (Р р г р р р- = .: = Т ^ Дж Используя формулу(9) можно увидеть: Кинетическая энергия блока K, который совершает плоское движение, определяется уравнением Т [п) ВХ — / м 2 г 2 Подставляя значение момента инерции блока к、 Формула называется (10) и (11) и вы получаете: Кинетическая энергия постепенно движущейся нагрузки L равна、 Нравится 7 ’©=.- !-7) 0.. 2(г Примените формулу (10) для определения: 74.)= я J