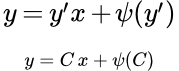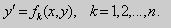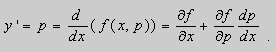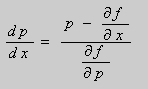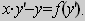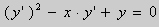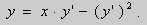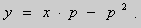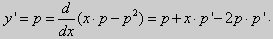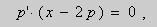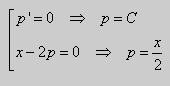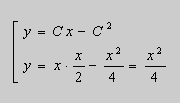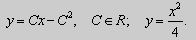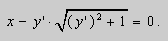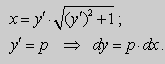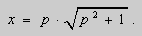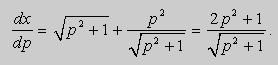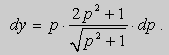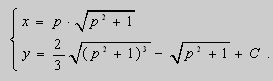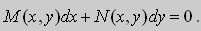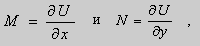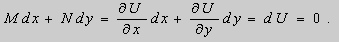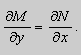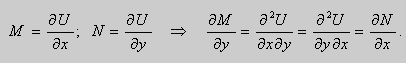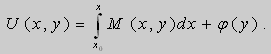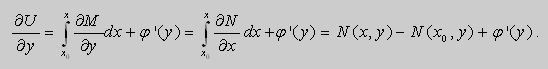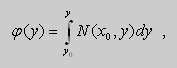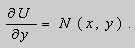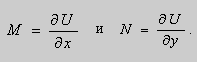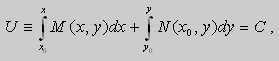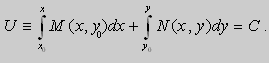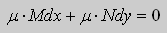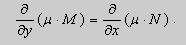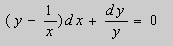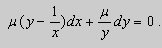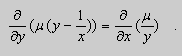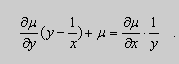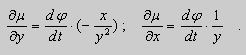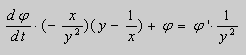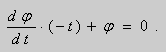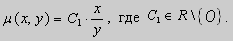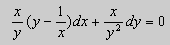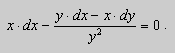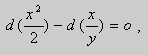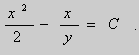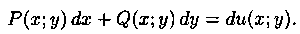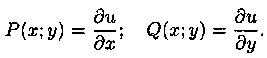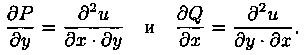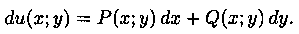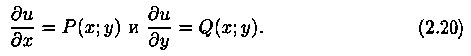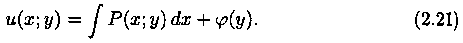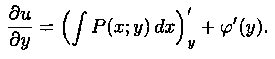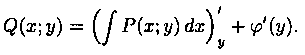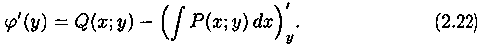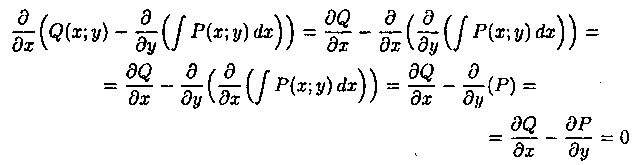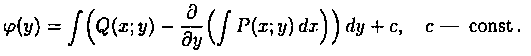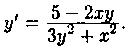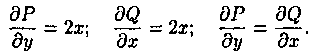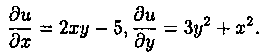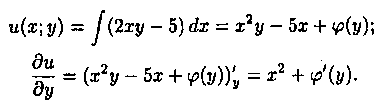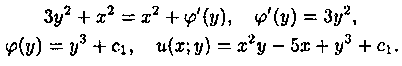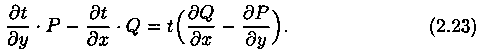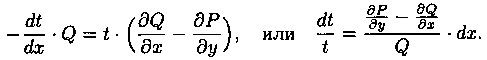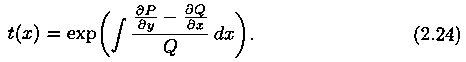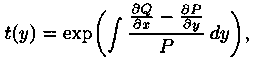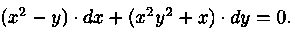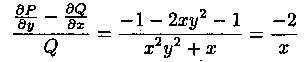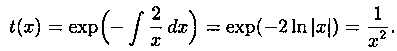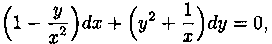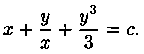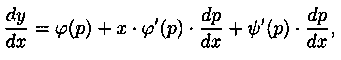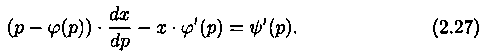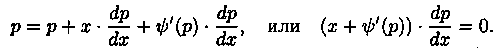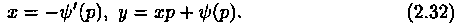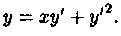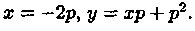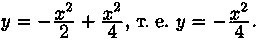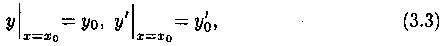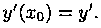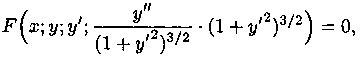Уравнения лагранжа и уравнение клеро

Видео:Курс по ОДУ: Уравнения Клеро и Лагранжа | Занятие 8Скачать

Дифференциальное уравнение Клеро

Видео:Решение уравнения ЛагранжаСкачать

Решение дифференциального уравнения Клеро

Рассмотрим уравнение Клеро:
(1)
Не трудно убедиться, что его общее решение имеет вид:
(2)

Действительно, поскольку – постоянная, то – тоже постоянная. Тогда дифференцируя (2) имеем:
;
(3) .
Подставляя (2) и (3) в (1), получаем тождество:
.

Видео:#Дифуры I. Урок 11. Уравнение Лагранжа . Уравнение КлероСкачать

Особое решение дифференциального уравнения Клеро

Уравнение Клеро может иметь особое решение. Как известно, если общее решение дифференциального уравнения имеет вид:
,
то особое решение может получиться исключением из уравнений:
;
.

В нашем случае, решение (2) можно записать в виде:
.
Тогда
.
Тогда особое решение может получиться, исключением из уравнений:
;
.

Поскольку возможны посторонние решения, то после нахождения особого решения, необходимо проверить, удовлетворяет ли он исходному уравнению (1).

Видео:Решение уравнения КлероСкачать

Пример

Решить уравнение:
(1.1)

Это уравнение Клеро. Его общее решение имеет вид:

Ищем особое решение. Перепишем общее решение в виде:
.
Дифференцируем по :

.
Тогда особое решение может получиться исключением из уравнений:
(1.2) ;
(1.3) .

Исключаем . Из уравнения (1.3) имеем:
(1.4) .
Возводим в квадрат и преобразуем:
;
;
. Отсюда следует, что .
Извлекаем квадратный корень:
(1.5) .
Поскольку мы возводили в квадрат, то, возможно, (1.5) содержит лишние решения, которые не удовлетворяют (1.4). Сейчас мы примем (1.5), а отсев лишних решений сделаем в самом конце.
Подставим (1.4) и (1.5) в (1.2):
.

Итак, особые решения имеют вид:
(1.6) .
Теперь сделаем проверку, чтобы выяснить, удовлетворяет ли исходному уравнению (1.1):
(1.1) .
Находим производную (1.6) и выполняем преобразования:

;
;
.
Подставляем в (1.1):
(1.7) .

При , . Уравнение (1.7) принимает вид:
.
Оно выполняется, если взять нижний знак:
.
То есть при , .

При , . Уравнение (1.7) принимает вид:
.
Оно выполняется, если взять верхний знак:
.
То есть при , .

Общее решение уравнения имеет вид:

При уравнение имеет особое решение:
.

При уравнение имеет особое решение:
.

Автор: Олег Одинцов . Опубликовано: 24-08-2012 Изменено: 10-04-2016

Видео:14. Уравнения Лагранжа и КлероСкачать

Лекция 2. Дифференциальные уравнения первого порядка, не разрешённые относительно производной .

Рассмотрим уравнение вида

F ( x , y , y ‘ ) = 0 ,

не разрешённое относительно производной. Если попытаться выразить из него y ‘ , то можно получить , вообще говоря , несколько уравнений

Геометрически это означает , что в каждой точке 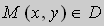задаётся несколько направлений поля (см.рис.2).

Следовательно через любую точку M ( x , y ) может проходить несколько интегральных кривых 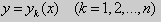. Для того, чтобы выделить из этого множества единственную интегральную кривую, проходящую через заданную точку M₀ ( x₀ , y₀) , надо помимо значений ( x₀ , y₀ ) дополнительно задать в этой точке направление поля y ‘ ( x₀) = y ‘_{0 .}

Задача Коши . Найти решение 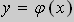уравнения F ( x , y , y ‘ ) = 0, удовлетворяющее начальным условиям y ( x₀) = y₀ и y ‘ ( x₀) = y ‘₀ , где y ‘₀ — решение уравнения F ( x₀ , y₀ , y ‘ ) = 0.

Теорема существования и единственности решения задачи Коши.

Пусть в некоторой окрестности U точки (x₀ , y₀ , y ‘₀ ), где y ‘₀ — решение уравнения F ( x₀ , y₀ , y ‘ ) = 0, выполнены условия :

1) F( x , y , y ‘ ) определена, непрерывна и имеет непрерывные частные производные F’_y и F’_{y ‘} по совокупности переменных ( x , y , y ‘ ) ;

2) значение производной F_y‘_‘ (x₀ , y₀ , y’₀ )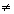0.

Тогда в некоторой окрестности точки x₀ существует единственное решение 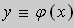уравнения F (x, y, y’) = 0, удовлетворяющее условиям y(x₀) = y₀ и y’ (x₀) = y’₀ .

Метод введения параметра.

На практике при решении уравнений F( x , y , y ‘ ) = 0 часто используют следующий метод.

Предположим , что уравнение F( x , y , y ‘ ) = 0 “легко” решить относительно y : y = f ( x , y ‘ ). Тогда введем замену y ‘ = p ( параметр зависит от x ). Предполагая, что дифференциальное уравнение имеет решение y = y ( x ) , получим ( в силу уравнения )

Из этих равенств выражаем :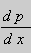

Это уравнение разрешено относительно производной 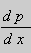. Пусть его общее решение имеет вид p = p ( x , C ) .Тогда общее решение заданного уравнения можно записать в виде y =f ( x , p ( x , C ) ). Решение найдено.

Таким методом можно решать , в частности , уравнения Лагранжа и Клеро.

Уравнение вида 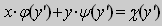называется уравнением Лагранжа. Оно является линейным относительно переменных x и y . Частным случаем этого уравнения является уравнение Клеро. Оно имеет вид :

Пример 1 . Решить уравнение

Решение. Выразим из уравнения (5) переменную y :

.Заменим 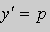и получим

Продифференцируем его по x :

Из этих равенств получаем :

После подстановки этих выражений в (6) будем иметь

Ответ :

Этим методом можно также решать уравнения , в которых «легко» выражается переменная x . Рассмотрим

Пример 2 . Решить уравнение

Решение . Выразим из уравнения (7) переменную x и введём параметр p :

Продифференцируем уравнение (8) по p :

Отсюда в силу равенства dy = p dx получим :

Проинтегрируем это уравнение :

Таким образом , с учётом ( 8 ) , получаем общее решение в параметрическом виде :

Примеры. Решить уравнения :

Уравнения в полных дифференциалах.

Если в уравнении (9) функции

В этом случае уравнение (9) называют уравнением в полных дифференциалах. После интегрирования получим общее решение уравнения

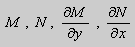
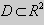
Теорема 1. Пусть функции непрерывные в некоторой односвязной области . Тогда необходимым и достаточным условием того, что уравнение (9) — в полных дифференциалах , является условие

Доказательство. 1. Необходимость.

Если выбрать функцию 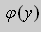та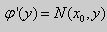к, чтобы

то и , следовательно ,

Таким образом , в уравнении (9)

Теорема 1 доказана.

Из теоремы следует , что общее решение уравнения (9) можно записать в виде

если 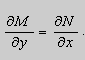Функцию U можно также представить в виде

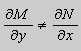
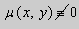
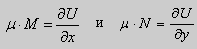
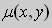
Предположим , что . Тогда можно попытаться найти такую функцию , чтобы . Функция называется интегрирующим множителем . В этом случае мы получаем уравнение

в полных дифференциалах. Следовательно, в силу теоремы 1,

Это уравнение позволяет найти интегрирующий множитель. Рассмотрим

Пример. Решить уравнение

Решение. Простой проверкой убеждаемся , что (10) не является уравнением в полных дифференциалах. Умножим его на неизвестную функцию :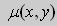

Попробуем найти 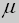из уравнения :

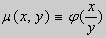
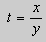
Пусть . Обозначим через и получим

После подстановки этих выражений в (11) будем иметь :

Проинтегрируем полученное уравнение :

Таким образом, интегрирующий множитель можно взять в виде

Умножим теперь уравнение (10) на функцию

Теорема 2. Если функции M и N непрерывные , имеют непрерывные частные производные первого порядка по x и по y , и 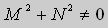, то интегрирующий множитель существует.

Замечание. Точка ( x₀ , y₀ ), в которой M ( x₀ , y₀ ) = N ( x₀ , y₀ ) = 0 является особой точкой уравнения (9). Поведение решений в окрестности особой точки изучается в лекции 3.

Примеры. Решить дифференциальные уравнения :

Видео:7.2. Уравнение Клеро: алгоритм решения и пример задачи, приводящей к уравнению КлероСкачать

Лекция № 3

Ссылки

2.5. Уравнение в полных дифференциалах. Интегрирующий множитель

называется ypaвнeниeм в пoлныx диффepeнциaлax, если его левая часть есть полный дифференциал некоторой функции υ(х; υ), т. е.

В этом случае ДУ (2.17) можно записать в виде du(x;y)=0, а его общий интеграл будет:

Приведем условие, по которому можно судить, что выражение

∆ =P(x;Y)dx+Q(x;y)dy есть полный дифференциал.

Пусть Δ есть полный дифференциал, т. е.

Учитывая, что 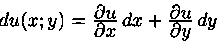(см. Часть 1, п. 44.3), имеем:

Дифференцируя эти равенства по υ и по х соответственно, получаем

А так как смешанные частные производные 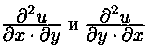равны между собой (см. Часть 1, п. 44.2), получаем (2.19).

Пусть в области D выполняется условие (2.19). Пока ж ем, что суще-ствует функция υ(х; υ) в области D такая, что

Найдем эту функцию. Искомая функция должна удовлетворять требованиям:

Если в первом уравнении (2.20) зафиксировать у и проинтегрировать его по х, то получим:

Здесь произвольная постоянная с= j (υ) зависит от у (либо является числом). В решении (2.21) не известна лишь j (υ). Для ее нахождения продифференцируем функцию (2.21) по υ:

Используя второе равенство (2.20), можно записать:

В равенстве (2.22) левая часть зависит от у. Покажем, что и правая часть равенства зависит только от у.Для этого продифференцируем правую часть по х и убедимся, что производная равиа нулю. Действительно,

в силу условия (2.19).

Из равенства (2.22) находим j (у):

Подставляя найденное значение для j (у) в равенство (2.21), находим функцию u(x; у) такую, что du(x; у)=Р(х; υ) dx+Q(x; у) dy.

Таким образом, при решении ДУ вида (2.17) сначала проверяем вы-полнение условия (2.19). Затем, используя равенства (2.20), находим функцию u(x;y). Решение записываем в виде (2.18).

Пример 2.11. Решить уравнение

Решение: Запишем уравнение в дифференциальной форме:

(2xy-5)dx+(3y 2 + x 2 )dу=0.

Здесь Р(х;у)=2ху- 5, Q(x;y)=Зу 2 +х2. Проверяем выполнение условия (2.19):

Следовательно, данное уравнсиие есть уравнение в полных дифференциалах. Условия (2.20) будут здесь выглядеть как

Общим интегралом является х 2 у — 5х+ у 3 +c₁=c₂, или х 2 у- 5х+ у 3 =с, где с=с₂-с₁.

Если условие (2.19) не выполняется, то ДУ (2.17) не является уравнениєм в полных дифференциалах.

О днако это уравнение иногда можно привести к уравнению в полных дифференциалах умножением его на некоторую функцию t(х;y), называемую интeгpирующим мнoжитeлeм.

Чтобы уравнение t(х;у)•Р(х;у)dx+t(х;y)•Q(x;y)dy=0 было уравнением в полных дифференциалах, должно выполняться условие

Выполнив дифференцирование 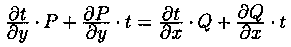и приведя подобные слагаемые, получим

Для нахождения Т(х; y) надо проинтегрировать полученное ДУ в частных производных. Решение этой задачи не простое. Нахождение интегрирующего множителя может быть упрощено, если допустить существование Т как функции только одного аргумента х либо только y. Пусть, например, Т=Т(х). Тогда уравнение (2.23) принимает вид

При этом выражениедолжно зависеть только от х.

Аналогично получаем, что если t=t(y) (t не зависит от х), то

а подынтегральное выражение должно зависеть только от у.

Пример 2.12. Решить уравнение

Решение: Здесьоднако

зависит только от х.

Следовательно, уравнение имеет интегрирующий множитель, зависящий только от х, выражение которого может быть получено при помощи формулы (2.24). В нашем случае получим, что

Умножая исходное уравнение на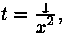получаем:

т. е. уравнение в полных дифференциалах! Решив его, найдем, что общий интеграл заданного уравнения имеет вид

2.6. Уравнения Лагранжа и Клеро

Рассмотрим дифференциальные уравнения, неразрешенные относительно производной. К ним, в частности, относятся уравнения Лагранжа и Клеро.

где j и Ψ — известные функции от 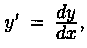называется урaвнeниeм Лагранжа.

Введем вспомогательный параметр, положив у ‘ =р. Тогда уравне-ние (2.25) примет вид

Дифференцируя по х, получим:

т. е.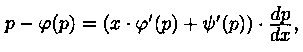или

Уравнение (2.27) есть линейное уравнение относительно неизвестной функции х= х(р). Решив его, найдем:

Исключая параметр р из уравнений (2.26) и (2.28), получаем общий интеграл уравнения (2.25) в виде у= γ (х;с).

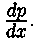
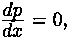
Отметим, что, переходя к уравнению (2.27), мы делили наПри этом могли быть потеряны решения, для которыхт. е. р=р_о=const.

Это значение р_о является корнем уравнения р- j (р)=0 (см. (2.27)).

Решеиие 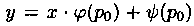является осоБым для уравнения (2.25)

(см. понятие особого решения в п. 2.2).

Рассмотрим частный случай уравнения Лагранжа при 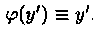Уравнение (2.25) принимает вид

и называется урaвнeниeм Клеро. Положив y ‘ =р, получаем:

Дифференцируя по х, имеем:

Если 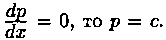Поэтому, с учетом (2.30), ДУ (2.29) имеет общее решение

Если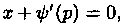то получаем частное решение уравнения в параметрической форме:

Это решение — особое решение уравнения Клеро: оно не содержится в формуле общего решения уравнения.

Пример 2.13. Решить уравнение Клеро

Решение: Общее решение, согласно формуле (2.31), имеет вид y=сх+с 2 . Особое решение уравнения получаем согласно формулам (2.32) в виде

Отсюда следует:

§3. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ

3.1. Основные понятия

Дифференциальные уравнения порядка выше первого называются ДУ высших порядков. ДУ второго порядка в общем случае записывается в виде

или, если это возможно, в виде, разрешенном относительно старшей производной:

Будем в основном рассматривать уравнение вида (3.2): от него всегда можно перейти к (3.1).

Решением ДУ (3.2) называется всякая функция у= j (х), которая при подстановке в уравнение обращает его в тождество.

ОБщим решением ДУ (3.2) называется функция у= j (х;с₁;с₂), где с₁ и с₂ — не зависящие от х произвольные постоянные, удовлетворяющая условиям:

1. j (х; с₁; с₂) является решением ДУ для каждого фиксированного значения с₁ и с₂.

2. Каковы бы ни были начальные условия

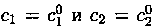
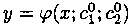
существуют единственные значения постоянныхтакие, что функцияявляется решением уравнения (3.2) и удовлетворяет начальным условиям (3.3).

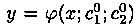
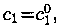
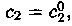
Всякое решениеуравнения (3.2), получающееся из общего решения у= j (х;с₁;с₂) при конкретных значениях постоянных называется частным решением.

Решения ДУ (3.2), записанные в виде 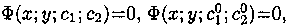называются общим и частным интегралом соответственно.

График всякого решения ДУ второго порядка называется интегральной крнвой. Общее решение ДУ (3.2) представляет собой множество ин-тегральных кривых; частное решение — одна интегральная кривая этого множества, проходящая через точку (х_о; у_о) и имеющая в ней касательную с заданным угловым коэффициентом

Переписав ДУ (3.1) в виде

видим, что ДУ второго порядка устанавливает связь между координатами точки (х; y) интегральной кривой, угловым коэффициентом k=y ‘ касательной к ней и кривизнойв точке (х; y). В этом состоит

геометрическое истолкование ДУ второго порядка.

Как и в случае уравнения первого порядка, задача нахождения решения ДУ (3.2), удовлетворяющего заданным начальным условиям (3.3), называется задачей Коши.

Примем теорему без доказательства.

Аналогичные понятия и определения имеют место для ДУ n-го порядка, которое в общем виде записывается как

или

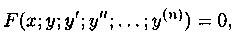
если его можно разрешить относительно старшей производной. Начальные условия для ДУ (3.4) имеют вид

Общее решение ДУ n-го порядка является функцией вида y= j (х;с₁;с₂;. ;с_n), содержащей n произвольных, не зависящих от х постоянных.

Решение ДУ (3.4), получающееся из общего решения при конкретных значениях постоянных с₁=с₀₁, с₂=с₀₂, . с_n=c_0n, называется частным решением.

Задача Коши для ДУ n-го порядка: найти решение ДУ (3.4), удовлетворяющее начальным условиям (3.5).

Проинтегрировать (решить) ДУ n-го порядка означает следующее: найти его общее или частное решение (интеграл) в зависимости от того, заданы начальные условия или нет.

Задача нахождения решения ДУ n-го порядка сложнее, чем первого. Поэтому рассмотрим лишь отдельные виды ДУ высших порядков.

📸 Видео

Дифференциальные уравнения не разрешенные относительно производной | poporyadku.schoolСкачать

9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Уравнение Клеро: world_type = real | Дифференциальные уравненияСкачать

Уравнения Лагранжа второго рода. Задача 1Скачать

Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать

Уравнение ЛагранжаСкачать

Уравнение КЛЕРО и остров ДИФФУРОВ | Дифференциальные уравненияСкачать

Уравнения Лагранжа #1Скачать

#Дифуры I. Урок 10. Уравнения, не разрешённые относительно производной. Метод введения параметраСкачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Уравнения Лагранжа второго родаСкачать

7.4. Уравнение ЛагранжаСкачать

ДУ Уравнения, не разрешенные относительно производнойСкачать