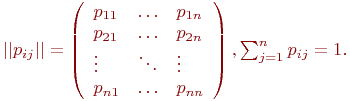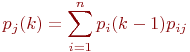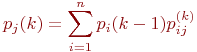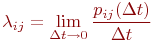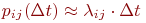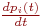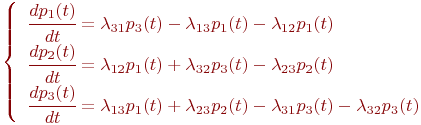Теорией случайных процессов называют раздел математики, изучающий закономерности случайных явлений в динамике их развития. Теория случайных процессов — это сравнительно новый раздел теории вероятностей, особенно интенсивно развивающийся в настоящее время в связи с широким кругом его практических приложений.
Содержание:
- Элементы теории случайных процессов и теории массового обслуживания
- Определение случайного процесса и его характеристики
- Основные понятия теории массового обслуживания
- Понятие марковского процесса
- Простейший поток событий
- Уравнения Колмогорова. Предельные вероятности состояний
- Уравнения Колмогорова. Предельные вероятности состояний
- Процесс гибели и размножения
- Марковские случайные процессы. Уравнения Колмогорова для вероятностей состояний.
- 🎥 Видео
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Элементы теории случайных процессов и теории массового обслуживания
Теория случайных процессов — это раздел математической науки, который изучает закономерности случайных явлений в динамике их развития.
Определение случайного процесса и его характеристики
Случайным процессом 

Реализацией случайного процесса называется детерминированная функция 

Количество реализаций определенного случайного процесса изображено на рис. 4.1. Пусть сечение процесса при данном 


Очевидно, что плотность вероятности 

Случайный процесс 


Таких сечений бесконечно много, но для задания случайного процесса удается ограничиться сравнительно небольшим количеством сечений.
Случайный процесс имеет порядок 





Случайный процесс может быть задан числовыми характеристиками.
Математическим ожиданием случайного процесса 



Дисперсией случайного процесса 



Средним квадратическим отклонением 

Математическое ожидание случайного процесса характеризует среднюю траекторию всех возможных его реализаций, а его дисперсия или среднее квадратическое отклонение — разброс реализаций относительно средней траектории.
Корреляционной функцией случайного процесса 
двух переменных 





Корреляционная функция 
Поэтому рассматривается также нормированная корреляционная функция случайного процесса.
Нормированной корреляционной функцией случайного процесса 
Пример. Случайный процесс определяется формулой 


Решение. Согласно свойствам математического ожидания и дисперсии получим:
Находим далее корреляционную функцию
а также нормированную корреляционную функцию
Случайные процессы можно классифицировать в зависимости от того, плавно или скачкообразно изменяются состояния системы, в которой они происходят, конечное или бесконечное множество этих состояний. Среди случайных процессов особое место занимают марковские случайные процессы, которые составляют основу теории массового обслуживания.
Основные понятия теории массового обслуживания
На практике часто приходится сталкиваться с системами, предназначенными для многоразового использования во время решения однотипных задач. Процессы, которые при этом происходят, называются процессами обслуживания, а соответствующие системы — системами массового обслуживания (СМО).
Примерами таких систем являются телефонные системы, ремонтные мастерские, вычислительные комплексы, кассы, где продаются железнодорожные или авиабилеты, магазины, парикмахерские и т.п.
Каждая МСО состоит из определенного количества обслуживаемых единиц (приборов, пунктов, станций), которые будем называть каналами обслуживания. Каналами могут быть линии связи, рабочие точки, вычислительные машины, продавцы и т.п. По количеству каналов СМО делятся на одно- и многоканальные.
Заявки поступают в СМО конечно нерегулярно, а случайно, образуя так называемый случайный поток заявок (ссылок). Обслуживание заявок также длится в течение определенного случайного времени. Учитывая случайность потока заявок и время обслуживания, СМО загружаются неравномерно: в определенные периоды накапливается очень много заявок (они или стают в очередь, или оставляют СМО не обслуженными), в другие периоды СМО работает с малой загрузкой или простаивает.
Предметом теории массового обслуживания является построение математических моделей, которые связывают заданные условия работы СМО с показателями ее эффективности, которые описывают способность этой системы обрабатывать потоки заявок.
Показателями эффективности СМО являются:
- — среднее количество заявок, которые она обслуживает за единицу времени;
- — среднее количество заявок в очереди;
- — среднее время ожидания обслуживания;
- — вероятность отказа в обслуживании без ожидания;
- — вероятность того, что количество заявок в очереди превышает определенное значение и т.д.
СМО делятся на два основных класса: СМО с отказами и СМО с ожиданием (очередью).
В СМО с отказами заявка, которая поступила в момент, когда все каналы были заняты, получив отказ, оставляет СМО и в дальнейшем процессе обслуживания не участвует.
В СМО с ожиданием заявка, которая поступает в момент, когда все каналы заняты, не оставляет систему, а становится в очередь на обслуживание.
Процесс работы СМО представляет собой случайный процесс.
Процесс называется процессом с дискретными состояниями, если его возможные состояния 
Процесс функционирования СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем.
Математический анализ работы СМО существенно упрощается, если процесс этой работы — марковский.
Понятие марковского процесса
Случайный процесс называется марковским, если для любого момента времени 

Пример. Система 






Некоторые процессы можно приблизительно считать марковскими.
Пример. Система 



Анализируя случайный процессы с дискретными состояниями, удобно пользоваться геометрической схемой — так называемым графом состояний Обычно состояния системы изображают прямоугольниками (кругами), а возможные переходы от одного состояния к другому — стрелками, которые соединяют состояния.
Пример. Построить граф состояний такого случайного процесса: прибор 
Решение. Возможные состояния системы: 



Граф системы приведен на рис. 4.2.
Стрелка, направленная из 





Для математического описания марковского случайного процесса с дискретными состояниями и непрерывным временем, которое происходит в СМО, рассмотрим одно из важных понятий теории вероятностей — понятие потока событий.
Простейший поток событий
Потоком событий называется последовательность событий, которые происходят один за другим в случайный момент времени Например, поток заявок, поступающий на предприятие бытового обслуживания, поток вызовов на телефонной станции, поток отказов (сбоев) во время работы на ЭВМ и т.д. Среднее количество событий, которые происходят за единицу времени, называется интенсивностью потока.
Поток называется простейшим, если он имеет такие свойства:
1) стационарность — вероятность того, что за некоторый промежуток времени 
2) отсутствие последействия — вероятность наступления некоторого количества событий в произвольном промежутке времени не зависит от того, какое количество событий произошло до начала этого промежутка;
3) ординарность — вероятность наступления двух и более событий за малый промежуток времени 
Если поток событий простейший, то вероятность того, что за промежуток времени 




Пример. Среднее количество заявок, поступающих на комбинат бытового обслуживания за 1 час равно 4. Найти вероятность того, что за 3 часа поступит: 1) 6 заявок; 2) менее 6 заявок; 3) не менее 6 заявок.
Решение. Пусть событие 


Уравнения Колмогорова. Предельные вероятности состояний
Вероятностью 


Очевидно, что для любого момента 
Правило построений уравнений Колмогорова. В левой части каждого из уравнений должна быть производная вероятности 

Например, для системы 

В системе (2) независимых уравнений на одно меньше от общего количества уравнений. Поэтому для решения системы необходимо прибавит уравнений (1) при
Особенность решения дифференциальных уравнений вообще состоит в том, что нужно задавать так называемые начальные условия, в данном случае — вероятности состояний системы в начальный момент 

Уравнения Колмогорова дают возможность находить все вероятности состояний как функции времени. Особый интерес представляет вероятности системы 

В теории случайных процессов доказано, что количество состояний системы конечное и из каждого из них можно перейти к любому другому состоянию, то предельные вероятности существуют.
Предельная вероятность состояния 


Пример 1. Найти предельные вероятности для системы 
Решение. Система алгебраических уравнений, которая описывает стационарный режим для данной системы, принадлежит к виду (1):
Решая эту систему уравнений, получаем 




Пример 2. Найти прибыль от эксплуатации в стационаром режиме системы 
Оценить экономическую эффективность уменьшения вдвое средней продолжительности ремонта каждого из этих узлов, если в этом случае придется вдвое увеличить расходы на ремонт.
Решение. Из примера 1 следует, что в среднем первый узел исправен в течение части времени, которая составляет 





Прибыль = 
Уменьшение вдвое среднего времени ремонта каждого из узлов согласно с 

Решая эту системы, получаем
Поскольку 
(Прибыль)

(Прибыль) 
Лекции:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Матрица интенсивностей. Система уравнений КолмогороваСкачать

Уравнения Колмогорова.
Предельные вероятности состояний
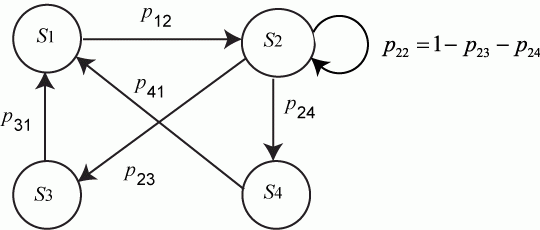
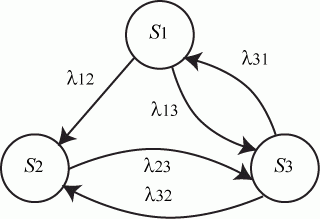
Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем* на примере случайного процесса из примера 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния в происходят под воздействием простейших потоков событий с интенсивностями ; так, переход системы из состояния в будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния в — под воздействием потока «окончаний ремонтов» первого узла и т.п.
Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система имеет четыре возможных состояния: .
Вероятностью i-го состояния называется вероятность того, что в момент система будет находиться в состоянии . Очевидно, что для любого момента сумма вероятностей всех состояний равна единице:
Рассмотрим систему в момент и, задав малый промежуток , найдем вероятность того, что система в момент будет находиться в состоянии . Это достигается разными способами.
1. Система в момент с вероятностью находилась в состоянии , а за время не вышла из него.
Вывести систему из этого состояния (см. граф на рис. 1) можно суммарным простейшим потоком с интенсивностью , т.е. в соответствии с формулой (7), с вероятностью, приближенно равной . А вероятность того, что система не выйдет из состояния , равна . Вероятность того, что система будет находиться в состоянии по первому способу (т.е. того, что находилась в состоянии и не выйдет из него за время ), равна по теореме умножения вероятностей:
2. Система в момент с вероятностями (или ) находилась в состоянии или и за время перешла в состояние .
Потоком интенсивностью (или — с- рис. 1) система перейдет в состояние с вероятностью, приближенно равной (или ). Вероятность того, что система будет находиться в состоянии по этому способу, равна (или ).
Применяя теорему сложения вероятностей, получим
Переходя к пределу при (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную (обозначим ее для простоты ):
Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.
Рассуждая аналогично для других состояний системы , можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:
Сформулируем правило составления уравнений Колмогорова . В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).
В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).
Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент . Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии , т.е. при начальных условиях .
Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени . Особый интерес представляют вероятности системы в предельном стационарном режиме , т.е. при , которые называются предельными (или финальными) вероятностями состояний.
В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.
Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии . Например, если предельная вероятность состояния , т.е. , то это означает, что в среднем половину времени система находится в состоянии .
Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы с графом состояний, изображенном на рис. 1), такая система уравнений имеет вид:
Систему (10) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом , согласно которому слева в уравнениях стоит предельная вероятность данного состояния , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.
Пример 2. Найти предельные вероятности для системы из примера 1, граф состояний которой приведен на рис. 1, при
Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или
(Здесь мы вместо одного «лишнего» уравнения системы (10) записали нормировочное условие (8)).
Решив систему (11), получим , т.е. в предельном, стационарном режиме система в среднем 40% времени будет находиться в состоянии (оба узла исправны), 20% — в состоянии (первый узел ремонтируется, второй работает), 27% — в состоянии (второй узел ремонтируется, первый работает) и 13% времени — в состоянии (оба узла ремонтируются)
Пример 3. Найти средний чистый доход от эксплуатации в стационарном режиме системы в условиях примеров 1 и 2, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден.ед., а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).
Решение. Из примера 2 следует, что в среднем первый узел исправно работает долю времени, равную , а второй узел — . В то же время первый узел находится в ремонте в среднем долю времени, равную , а второй узел — . Поэтому средний чистый доход в единицу времени от эксплуатации системы, т.е. разность между доходами и затратами, равен
Уменьшение вдвое среднего времени ремонта каждого из узлов в соответствии с (6) будет означать увеличение вдвое интенсивностей потока «окончаний ремонтов» каждого узла, т.е. теперь и система линейных алгебраических уравнений (10), описывающая стационарный режим системы , вместе с нормировочным условием (8) примет вид:
Решив систему, получим .
Учитывая, что , а затраты на ремонт первого и второго узла составляют теперь соответственно 8 и 4 ден.ед., вычислим средний чистый доход в единицу времени:
Так как больше (примерно на 20%), то экономическая целесообразность ускорения ремонтов узлов очевидна.
Видео:уравнение колмагороваСкачать

Процесс гибели и размножения
В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения . Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.
Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.
Рассмотрим упорядоченное множество состояний системы . Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния возможны переходы только либо в состояние , либо в состояние .
Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями или .
По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).
В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния
для состояния имеем , которое с учетом (12) приводится к виду
Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:
к которой добавляется нормировочное условие
При анализе численности популяций считают, что состояние соответствует численности популяции, равной , и переход системы из состояния в состояние происходит при рождении одного члена популяции, а переход в состояние — при гибели одного члена популяции.
Решая систему (14), (15), можно получить
Легко заметить, что в формулах (17) для коэффициенты при есть слагаемые, стоящие после единицы в формуле (16). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния , а знаменатели — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния .
Пример 4. Процесс гибели и размножения представлен графом (рис. 5). Найти предельные вероятности состояний.
Видео:Решение системы уравнений Колмогорова в МатлабеСкачать

Марковские случайные процессы. Уравнения Колмогорова для вероятностей состояний.
Наиболее полное исследование процесса функционирования систем получается, если известны явные математические зависимости, связывающие искомые показатели с начальными условиями, параметрами и переменными исследуемой системы. Для многих современных систем, являющихся объектами моделирования, такие математические зависимости отсутствуют или малопригодны, и следует применять другое моделирование, как правило, имитационное.
Большой класс случайных процессов составляют процессы без последействия, которые в математике называют марковскими процессами в честь Андрея Андреевича Маркова — старшего (1856 — 1922), выдающегося русского математика, разработавшего основы теории таких процессов.
Случайный процесс называется марковским, если вероятность перехода системы в новое состояние зависит только от состояния системы в настоящий момент и не зависит от того, когда и каким образом система перешла в это состояние.
Практически любой случайный процесс является марковским или может быть сведен к марковскому. В последнем случае достаточно в понятие состояния включить всю предысторию смен состояний системы.
Марковские процессы делятся на два класса:
· дискретные марковские процессы (марковские цепи);
· непрерывные марковские процессы.
Дискретной марковской цепьюназывается случайный процесс, при котором смена дискретных состояний происходит в определенные моменты времени.
Непрерывным марковским процессомназывается случайный процесс, при котором смена дискретных состояний происходит в случайные моменты времени.
Рассмотрим ситуацию, когда моделируемый процесс обладает следующими особенностями.
Система 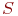
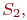
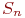
Смена состояний происходит, будем считать, мгновенно и в строго определенные моменты времени 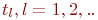
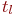
Известны вероятности перехода 

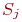
Цель моделирования: определить вероятности состояний системы после 
Обозначим эти вероятности 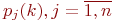

Если в системе отсутствует последействие, то есть вероятности 

Марковская цепь называется однородной, если переходные вероятности 
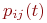
Значения 
Значения 
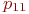
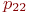
Не указываются также нулевые вероятности переходов. Например, на рис. это вероятности 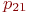
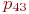
Математической моделью нахождения вероятностей состояний однородной марковской цепи является рекуррентная зависимость
где 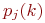
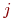

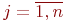
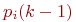
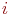

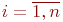
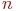

Рис.Размеченный граф состояний системы
Для неоднородной марковской цепи вероятности состояний системы находятся по формуле:
где 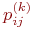

Сформулируем методику моделирования по схеме дискретных марковских процессов (марковских цепей).
1. Зафиксировать исследуемое свойство системы.
Определение свойства зависит от цели исследования. Например, если исследуется объект с целью получения характеристик надежности, то в качестве свойства следует выбрать исправность. Если исследуется загрузка системы, то — занятость. Если состояния объектов, то — поражен или непоражен.
2. Определить конечное число возможных состояний системы и убедиться в правомерности моделирования по схеме дискретных марковских процессов.
3. Составить и разметить граф состояний.
4. Определить начальное состояние.
5. По рекуррентной зависимости определить искомые вероятности.
В рамках изложенной методики моделирования исчерпывающей характеристикой поведения системы является совокупность вероятностей 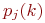
При моделировании состояния систем с непрерывными марковскими процессами мы уже не можем воспользоваться переходными вероятностями 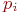

Поэтому вместо переходных вероятностей вводятся в рассмотрение плотности вероятностей переходов 
где 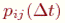


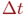
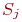
С точностью до бесконечно малых второго порядка из приведенной формулы можно представить:
Непрерывный марковский процесс называется однородным,если плотности вероятностей переходов 

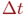
Целью моделирования,как и в случае дискретных процессов, является определение вероятностей состояний системы 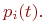
Сформулируем методику моделирования по схеме непрерывных марковских процессов.
1. Определить состояния системы и плотности вероятностей переходов 
2. Составить и разметить граф состояний.
3. Составить систему дифференциальных уравнений Колмогорова. Число уравнений в системе равно числу состояний. Каждое уравнение формируется следующим образом.
4. B левой части уравнения записывается производная вероятности 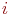
5. В правой части записывается алгебраическая сумма произведений 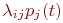
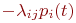
6. Определить начальные условия и решить систему дифференциальных уравнений.
Пример. Составить систему дифференциальных уравнений Колмогорова для нахождения вероятностей состояний системы, размеченный граф состояний которой представлен на рисунке.
Рис. Размеченный граф состояний
Очевидно, 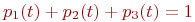
Поэтому любое из первых трех уравнений можно исключить, как линейно зависимое.
Для решения уравнений Колмогорова необходимо задать начальные условия. Для рассмотренного примера можно задать такие начальные условия: 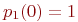
Дата добавления: 2015-04-03 ; просмотров: 7855 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
🎥 Видео
Решение системы уравнений методом ГауссаСкачать

Калькулятор не поможет ★ Жесть от Колмогорова ★ Что больше 2^3^100 или 3^2^150 ★ Сравните числаСкачать

Математика это не ИсламСкачать

Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Олегу Тинькову запрещён вход на Мехмат МГУСкачать

Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

День студента мехмата МГУ #мгу #умскул #физика #математика #учеба #подготовкаогэ #подготовкакегэСкачать

О единственности вероятностных решений уравнений Фоккера-Планка-КолмогороваСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Математика без Ху!ни. Теория вероятностей. Схема БернуллиСкачать

Уравнения Фоккера-Планка-Колмогорова (С.В. Шапошников)Скачать