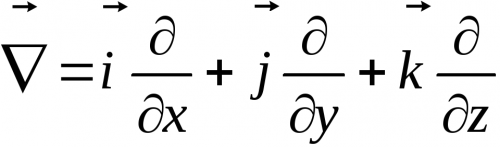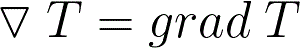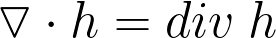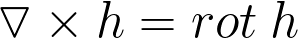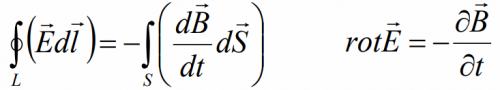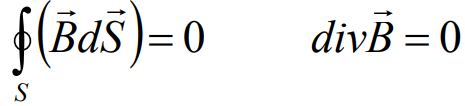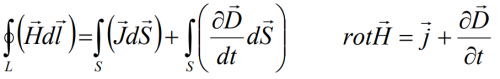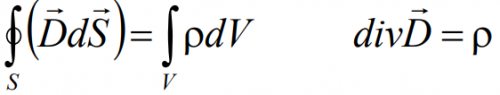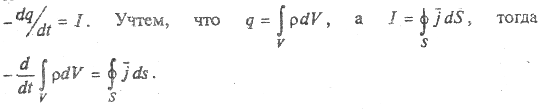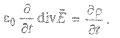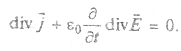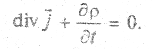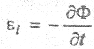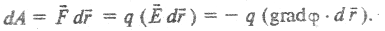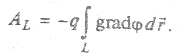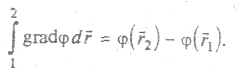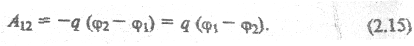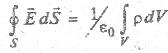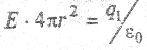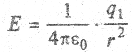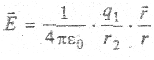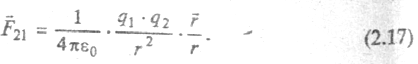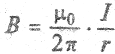- Уравнения Максвелла для электромагнитного поля — основные законы электродинамики
- Уравнений классической электродинамики (уравнения Максвелла)
- Уравнения Максвелла
- Уравнения Максвелла в дифференциальной форме
- Уравнение 1: Закон Гаусса или Теорема Гаусса
- Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)
- Уравнение 3: Закон Гаусса для магнетизма
- Уравнение 4: Закон Ампера
- Уравнения Максвелла в интегральной и дифференциальной форме
- Уравнение 1: Закон Гаусса (Теорема Гаусса)
- Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)
- Уравнение 3: Закон Гаусса для магнетизма
- Уравнение 4: Закон Ампера
- 💡 Видео
Уравнения Максвелла для электромагнитного поля — основные законы электродинамики
Система уравнений Максвелла обязана своим названием и появлением Джеймсу Клерку Максвеллу, сформулировавшему и записавшему данные уравнения в конце 19 века.
Максвелл Джемс Кларк (1831 — 1879) был известным британским физиком и математиком, профессором Кембриджского университета в Англии.
Он практически объединил в своих уравнениях все накопленные к тому времени экспериментально полученные результаты касательно электричества и магнетизма и придал законам электромагнетизма четкую математическую форму. Основные законы электродинамики (уравнения Максвелла) были сформулированы в 1873 году.
Максвелл развил учение Фарадея об электромагнитном поле в стройную математическую теорию, из которой вытекала возможность волнового распространения электромагнитных процессов. При этом оказалось, что скорость распространения электромагнитных процессов равна скорости света (величина которой была уже известна из опытов).
Это совпадение послужило для Максвелла основанием к тому, чтобы высказать идею об общей природе электромагнитных и световых явлений, т.е. об электромагнитной природе света.
Созданная Джеймсом Максвеллом теория электромагнитных явлений нашла первое подтверждение в опытах Герца, впервые получившего электромагнитные волны.
В итоге эти уравнения сыграли главную роль в формировании точных представлений классической электродинамики. Уравнения Максвелла могут быть записаны в дифференциальной или интегральной форме. Практически они описывают сухим языком математики электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и в сплошных средах. К данным уравнениям можно добавить выражение для силы Лоренца, в этом случае мы получим полную систему уравнений классической электродинамики.
Чтобы понимать некоторые математические символы, использующиеся в дифференциальных формах уравнений Максвелла, для начала определим такую занятную вещь, как оператор набла.
Оператор набла (или оператор Гамильтона) — это векторный дифференциальный оператор, компоненты которого являются частными производными по координатам. Для нашего реального пространства, которое является трехмерным, адекватна прямоугольная система координат, для которой оператор набла определяется следующим образом:
где i, j и k – единичные координатные векторы
Оператор набла, будучи применен к полю тем или иным математическим образом, дает три возможные комбинации. Данные комбинации именуются:
Градиент — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.
Дивергенция (расхождение) — дифференциальный оператор, отображающий векторное поле на скалярное (то есть, в результате применения к векторному полю операции дифференцирования получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле», точнее, насколько расходятся входящий и исходящий потоки.
Ротор (вихрь, ротация) — векторный дифференциальный оператор над векторным полем.
Теперь рассмотрим непосредственно уравнения Максвелла в интегральной (слева) и дифференциальной (справа) формах, содержащие в себе основные законы электрического и магнитного полей, включая электромагнитную индукцию.
Интегральная форма: циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.
Дифференциальная форма: при всяком изменении магнитного поля возникает вихревое электрическое поле, пропорциональное скорости изменения индукции магнитного поля.
Физический смысл: всякое изменение магнитного поля во времени вызывает появление вихревого электрического поля.
Интегральная форма: поток индукции магнитного поля через произвольную замкнутую поверхность равен нулю. Это означает, что в природе нет магнитных зарядов.
Дифференциальная форма: поток силовых линий индукции магнитного поля из бесконечного элементарного объёма равен нулю, так как поле вихревое.
Физический смысл: источники магнитного поля в виде магнитных зарядов в природе отсутствуют.
Интегральная форма: циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру прямо пропорциональна суммарному току, пересекающему поверхность, охватываемую этим контуром.
Дифференциальная форма: вокруг любого проводника с током и вокруг любого переменного электрического поля существует вихревое магнитное поле.
Физический смысл: протекание тока проводимости по проводникам и изменения электрического поля во времени приводят к появлению вихревого магнитного поля.
Интегральная форма: поток вектора электростатической индукции через произвольную замкнутую поверхность, охватывающую заряды, прямо пропорционален суммарному заряду, расположенному внутри этой поверхности.
Дифференциальная форма: поток вектора индукции электростатического поля из бесконечного элементарного объема прямо пропорционален суммарному заряду, находящемуся в этом объёме.
Физический смысл: источником электрического поля является электрический заряд.
Система данных уравнений может быть дополнена системой так называемых материальных уравнений, которые характеризуют свойства заполняющей пространство материальной среды:
Видео:Система уравнений Максвелла. Связь интегральной и дифференциальной формы уравнений.Скачать

Уравнений классической электродинамики (уравнения Максвелла)
Всякое решение уравнений поля должно описывать поле, которое может существовать в Природе, Согласно принципу суперпозиции, сумма любых таких полей также должна представлять реально возможное поле. Линейные дифференциальные уравнения обладают таким свойством, что сумма любых решений уравнения также является его решением. Следовательно, уравнения электромагнитного поля должны быть линейными дифференциальными уравнениями.
Система уравнений, описывающих электромагнитное поле, называется уравнениями Максвелла. Они являются основными уравнениями классической электродинамики Уравнения Максвелла связывают в любой точке пространства и в любой момент времени силовые характеристики, определяющие электромагнитное поле ( 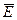
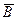
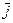
Первое уравнение определяет, что электрическое поле порождается электрическими зарядами; это уравнение устанавливает связь между объемной плотностью заряда ρ и вектором 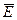
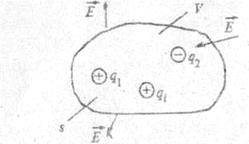 |
Пусть в пространстве выделена некоторая область объемом V, ограниченная замкнутой поверхностью S, а в этом объеме произвольным образом распределен заряд q, так, что объемная плотность заряда ρ (рис. 2.2). Это означает, что 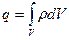
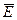
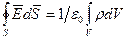
Здесь ε0— постоянный коэффициент, называемый электрической постоянной.
Силовые линии электрического поля, созданного зарядами, разомкнуты, они начинаются и оканчиваются на зарядах или уходят в бесконечность.
Второе уравнение определяет еще один источник электрического поля — изменяющееся во времени магнитное поле. Это уравнение является обобщением закона электромагнитной индукции Фарадея.
Пусть в пространстве выделен некоторый замкнутый контур L, ограничивающий поверхность S. Пусть существует магнитное поле индукцией 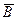
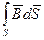
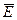
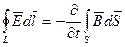
Чем быстрее изменяется магнитное поле, тем сильнее возникающее при этом (индуцированное) электрическое поле. Индуцированное поле носит вихревой характер. Знак “минус” перед правой частью уравнения (2.6) отвечает правилу Ленца.
Третье уравнение определяет факт отсутствия в Природе магнитных зарядов (подобных электрическим) как источников магнитного поля; поток вектора магнитной индукции через произвольную замкнутую поверхность S равен нулю:
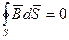
Магнитное поле всегда носит вихревой характер; магнитные силовые линии всегда замкнуты.
Четвертое уравнение определяет, что источником магнитного поля являются движущиеся электрические заряды (т. е. электрический ток) и изменяющееся во времени электрическое поле:
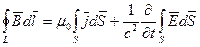
Циркуляция вектора 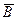
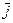
Из (2.6) и (2.8) следует, что электрическое и магнитное поля нельзя в общем случае рассматривать независимо. Они составляют неразрывную совокупность — электромагнитное поле. К этому вопросу мы вернемся при изучении теории относительности
Рассмотренные уравнения (2.5) — (2.8) называются интегральными. Их можно записать с использованием дифференциальных характеристик (МП 5.2) в виде системы дифференциальных уравнений:
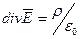
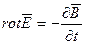
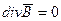
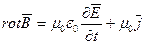
Переход к дифференциальной форме осуществляется с помощью теорем Гаусса и Стокса (МП 5.4). Покажем для примера связь между уравнениями (2.5) и (2.5′). На основании теоремы Гаусса левая часть уравнения (2.5) преобразуется к интегралу по объему 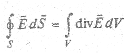
С использованием дифференциальных характеристик удобно сформулировать закон сохранения электрического заряда. Так как заряд электрически изолированной системы сохраняется, то уменьшение заряда в некотором объеме в единицу времени равно силе тока через поверхность, ограничивающую этот объем, т. е.
Применим к правой части интегральную теорему Гаусса:
где интегрирование ведется по одному и тому же объему, следовательно,
Полученное уравнение называется уравнением непрерывности.
Четыре рассмотренных уравнения поля в интегральной и дифференциальной формах представляют собой единую систему уравнений Максвелла для электромагнитного поля в вакууме. Она полностью определяет электромагнитное поле, если известны расположение и движение электрических зарядов. Уравнение Максвелла вместе с выражением для силы Лоренца (2.3) представляют наиболее общие законы электромагнетизма. Все остальное содержание электродинамики составляют выводы и следствия, полученные с помощью математических преобразований уравнений Максвелла-Лоренца для конкретных систем полей, зарядов и токов.
Например, из уравнений (2.5′) и (2.8′) следует закон сохранения электрического заряда в форме (2.9). Продифференцировав обе части уравнения (2.5′) по времени, получим:
Обе части уравнения (2.8′) умножим на 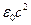
Дивергенция от ротора любого вектора по определению равна нулю. В правой части (2.10) поменяем местами операции дифференцирования и дивергенции:
Заменяя второй член этого уравнения на 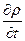
Прямо вытекает из второго уравнения Максвелла (2.6) закон электромагнитной индукции Фарадея. Интеграл в правой части уравнения по определению есть магнитный поток 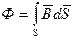
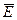
Стационарные электрические и магнитные доля существуют, если расположение зарядов неизменно во времени и электрические токи постоянны. В этом случае 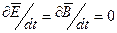
Первая пара уравнений описывает электростатическое поле (поле неподвижных зарядов), а вторая — магнитостатическое (поле постоянных токов). Из уравнений следует, что электростатическое поле потенциальное, а магнитостатическое — вихревое.
Важной характеристикой электростатического поля является потенциал, характеризующий потенциальную энергию заряда, находящегося в поле. Пусть заряд помещен в некоторую точку электростатического поля. Тогда потенциалом φ называется отношение потенциальной энергии U этого заряда к величине заряда:
На заряд действует со стороны поля сила, стремящаяся уменьшить его потенциальную энергию: 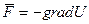
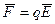
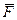
Формула (2.14) описывает связь напряженности и потенциала для электростатического поля.
Сила 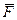
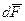
Работа сил поля на некотором участке траектории L определяется интегралом
Из свойств интеграла (МП 3.2) следует, что интеграл от гpaдиента потенциала на некотором участке траектории 1-2 равен разности значений потенциала на концах участка, т. е.
Здесь 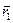
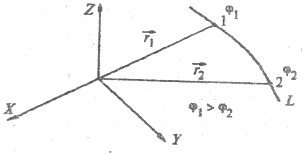 |
Важно, что работа не зависит от вида траектории, а определяется только положением начала и конца последней. С выражением (2.15) связана широко используемая в атомной физике и физике элементарных частиц внесистемная единица энергии — электровольт (эВ). 1 эВ — энергия, приобретаемая одним элементарным зарядом (е) при прохождении им разности потенциалов 1 В. Из (2.15) непосредственно следует, что работа сил потенциального поля при перемещении заряда по замкнутому контуру равна нулю, так как в этом случае 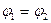
Вернемся к выражению элементарной работы 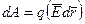
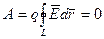
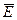
Выражение (2.16) дает необходимое и достаточное условие потенциальности поля. В противоположность электростатическому магнитостатическое поле является вихревым и характеризуется не скалярным, а векторным потенциалом.
Рассмотрим вывод из уравнений Максвелла некоторых законов электромагнетизма, полученных эмпирически.
Поле точечного заряда. Закон Кулона. Этот закон определяет силу взаимодействия двух неподвижных точечных зарядов в вакууме.
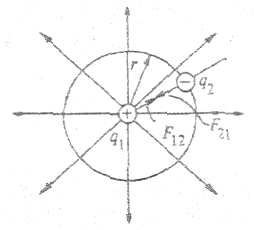
Линии напряженности (силовые линии) поля, создаваемого этим зарядом, радиальны, поле обладает центральной симметрией. На поверхности сферы значение 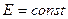
Воспользуемся ‘ первым уравнением Максвелла (2.5) —теоремой Гаусса
которое при выбранных условиях преобразуется к простому виду
Направление вектора 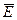
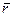
Полученная формула определяет напряженность электрического поля точечного заряда в точках, удаленных от него на расстояние r. Поместим в любую точку на поверхности сферы другой точечный заряд q2, например, отрицательный. По определению напряженности, на него будет действовать сила притяжения — кулоновская сила.
Если в наших рассуждениях заряды поменять местами, получим, что на заряд q1 со стороны q2, действует сила 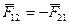

Направление силовых линий связано с направлением тока правилом правою винта. Предположим, что переменное электрическое поле отсутствует, тоща уравнение (2.8) упростится:
Выберем одну из силовых линий радиуса r. Тогда в выражении (2.18)
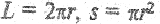
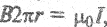
Эта формула определяет модуль вектора магнитной индукции магнитного поля, создаваемого током I в точках, отстоящих от проводника на расстояние r.
Дата добавления: 2017-11-21 ; просмотров: 2194 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:О чем говорят уравнения Максвелла? Видео 1/2Скачать

Уравнения Максвелла
Уравнения Максвелла — это 4 уравнения, которые описывают, как электрические и магнитные поля распространяются и взаимодействуют; т.е. эти уравнения (правила или даже законы) описывают процессы/взаимодействия электромагнетизма.
Эти правила описывают, как проходит управление поведением электрических и магнитных полей. Уравнения Максвелла показывают, что электрический заряд (положительный и отрицательный):
- Порождает электрическое поле (также если заряд изменяется со временем, то он вызывает появление электрического поля).
- В дальнейшем он вызывает появление магнитного поля.
Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Уравнения Максвелла в дифференциальной форме
Уравнение 1: Закон Гаусса или Теорема Гаусса
Дивергенция электрического поля равняется плотности заряда. Существует вязь между электрическим полем и электрическим зарядом.
Дивергенция в физике показывает, насколько данная точка пространства является источником или потребителем потока поля.
Очень кратко: Электрические поля расходятся от электрических зарядов: электрический заряд создаёт поле вокруг себя и, таким образом, действует как источник электрических полей. Это можно сравнить с краном, который является источником воды.
Ещё закон Гаусса говорит о том, что отрицательные заряды действуют как сток для электрических полей (способ, как вода стекает через отверстие стока). Это означает, что линии электрического поля имеют начало и поглощаются при электрическом заряде.
Заряды с одинаковым знаком отталкиваются друг от друга, а противоположные заряды притягиваются друг к другу (если есть два положительных заряда, они будут отталкиваться; а если есть один отрицательный и один положительный, они будут притягиваться друг к другу).
Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)
Можно создать электрическое поле, изменив магнитное поле.
Очень кратко: Закон Фарадея гласит, что изменяющееся магнитное поле внутри контура вызывает индуцированный ток, который возникает из-за силы или напряжения внутри контура. Это значит:
- Электрический ток порождает магнитные поля, а эти магнитные поля (вокруг цепи) вызывают электрический ток.
- Изменяющееся во времени магнитное поле вызывает распространение электрического поля.
- Циркулирующее во времени электрическое поле вызывает изменение магнитного поля во времени.
Уравнение 3: Закон Гаусса для магнетизма
Дивергенция магнитного потока любой замкнутой поверхности равна нулю. Магнитного монополя не существует.
Закон Гаусса для магнетизма утверждает (очень кратко):
- Магнитных монополей не существует.
- Расхождение полей B или H всегда равно нулю в любом объёме.
- На расстоянии от магнитных диполей (это круговой ток) магнитные поля текут по замкнутому контуру.
Уравнение 4: Закон Ампера
Магнитное поле создаётся с помощью тока или изменяющегося электрического поля.
Очень кратко: Электрический ток порождает магнитное поле вокруг тока. Изменяющийся во времени электрический поток порождает магнитное поле.
Видео:Тригонометрические уравнения № 13 ЕГЭ 2024Скачать

Уравнения Максвелла в интегральной и дифференциальной форме
Вспомним сначала в дифференциальной форме и следом будет в интегральной форме.
Уравнение 1: Закон Гаусса (Теорема Гаусса)
Это же уравнение в интегральной форме:
Поток вектора электрической индукции D через любую замкнутую поверхность равняется сумме свободных зарядов, охваченных этой поверхностью. Электрическое поле создаётся нескомпенсированными электрическими зарядами (это те, что создают вокруг себя своё собственное электрическое поле).
Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)
И это же уравнение в интегральной форме:
Циркуляция вектора напряжённости Е вихревого электрического поля (по любому замкнутому контуру) равняется скорости изменения магнитного потока через площадь контура (S) с противоположным знаком.
Уравнение 3: Закон Гаусса для магнетизма
И это же уравнение в интегральной форме:
Силовые линии магнитного поля замкнуты, т.к. поток вектора индукции В магнитного поля через любую замкнутую поверхность равняется нулю.
Уравнение 4: Закон Ампера
И это же уравнение в интегральной форме:
Циркуляция вектора напряжённости Н магнитного поля по замкнутому контуру равняется алгебраической сумме токов, которые пронизывают этот контур. Магнитное поле создаётся не только током проводимости, но и переменным электрическим полем.
💡 Видео
Билеты №32, 33 "Уравнения Максвелла"Скачать

Электромагнетизм Л11.1. Уравнения Максвелла в интегральной формеСкачать

Электродинамика | закон Ома в интегральной формеСкачать

3 14 Уравнения МаксвеллаСкачать

Электродинамика | уравнения Максвелла | 1 | для взрослыхСкачать
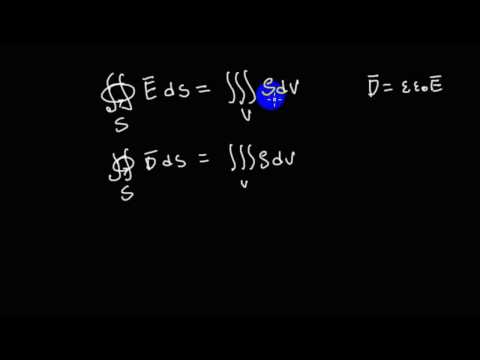
ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать

ЧК_МИФ /ЛИКБЕЗ/ 3_3_5_1 СИСТЕМА УРАВНЕНИЙ МАКСВЕЛЛА. ПРИМЕРЫ (минимум теории)Скачать

Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

Экскурсия по классической электродинамикеСкачать

Основные физические понятия технической электродинамики, 1978Скачать
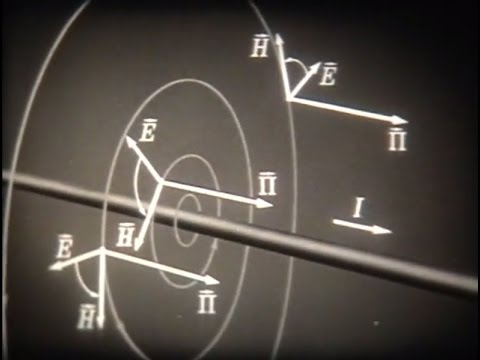
Закон КулонаСкачать

Тургенбаев Досжан Нурмагамбетович 8 СИСТЕМА УРАВНЕНИЙ МАКСВЕЛЛА ПЕРВОЕ УРАВНЕНИЕ МАКСВЕЛЛАСкачать

Чирцов А.С. "Бессильные линии". Уравнения Максвелла. Электромагнитные волны. Оператор. Производная.Скачать

ЧК_МИФ: 4.1.1. Уравнение ДеламбераСкачать

Вывод уравнения электромагнитной волныСкачать

Уравнения Максвелла 2021Скачать