Уравнения касательных к гиперболе x2 4y2 16 проведенных из точек a 0 2

Условие

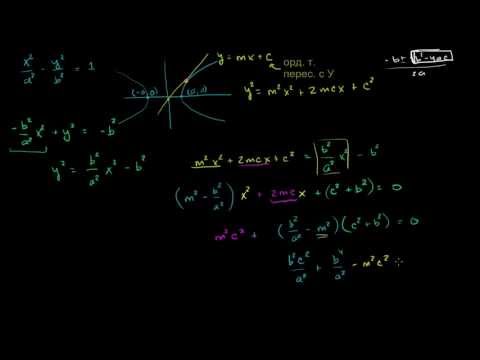
найти уравнение касательных к гиперболе x^2/5-y^2/4=1 параллельных прямой x+y-4=0

Решение

x + y — 4 = 0 ⇒ y= — x + 4

Значит, касательные || прямой имеют вид

Прямая y=-x+b и гипербола y^2=(4/5)x^2 — 4
имеют одну общую точку, т. е

(4/5)x^2-4=(-x+b)^2 имеет единственное решение

Квадратное уравнение имеет один корень, если D=0

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Калькулятор онлайн.
Уравнение прямой касательной к графику функции в заданной точке

Эта математическая программа находит уравнение касательной к графику функции ( f(x) ) в заданной пользователем точке ( x_0 ).

Программа не только выводит уравнение касательной, но и отображает процесс решения задачи.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Статью из энциклопедии о касательной прямой вы можете посмотреть здесь (статья из Википедии).

Если вам нужно найти производную функции, то для этого у нас есть задача Найти производную.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> Введите выражение функции ( f(x)) и число (x_0) — абсциссу точки в которой нужно построить касательную Найти уравнение касательной

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Немного теории.

Видео:найти уравнение касательной к эллипсуСкачать

Угловой коэффициент прямой

Напомним, что графиком линейной функции ( y=kx+b) является прямая. Число (k=tg alpha ) называют угловым коэффициентом прямой, а угол ( alpha ) — углом между этой прямой и осью Ox

Видео:Уравнение касательнойСкачать

Уравнение касательной к графику функции

Если точка М(а; f(a)) принадлежит графику функции у = f(x) и если в этой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то из геометрического смысла производной следует, что угловой коэффициент касательной равен f'(a). Далее мы выработаем алгоритм составления уравнения касательной к графику любой функции.

Пусть даны функция у = f(x) и точка М(а; f(a)) на графике этой функции; пусть известно, что существует f'(a). Составим уравнение касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат, имеет вид y = kx + b, поэтому задача состоит в нахождении значений коэффициентов k и b.

С угловым коэффициентом k все понятно: известно, что k = f'(a). Для вычисления значения b воспользуемся тем, что искомая прямая проходит через точку М(а; f(a)). Это значит, что если подставить координаты точки М в уравнение прямой, получим верное равенство: (f(a)=ka+b ), т.е. ( b = f(a) — ka ).

Осталось подставить найденные значения коэффициентов k и b в уравнение прямой:

Нами получено уравнение касательной к графику функции ( y = f(x) ) в точке ( x=a ).

Алгоритм нахождения уравнения касательной к графику функции ( y=f(x) )
1. Обозначить абсциссу точки касания буквой ( a )
2. Вычислить ( f(a) )
3. Найти (f'(x) ) и вычислить (f'(a) )
4. Подставить найденные числа ( a, f(a), f'(a) ) в формулу ( y=f(a)+ f'(a)(x-a) )

Видео:Уравнение касательной в точке. Практическая часть. 2ч. 10 класс.Скачать

Урок по теме «Уравнение касательной к графику» для 10-х классов с углубленным изучением математики

Разделы: Математика

Тема: Уравнение касательной к графику.

Цель урока: повторить теоретические знания по данной теме, закрепить их при решении задач.

Ход урока

1. Устная работа

1) Геометрический смысл производной.

— Если к графику функции у = f(x) в точке с абсциссой х₀ можно провести касательную не параллельную оси Оу, то производная данной функции в точке х₀ выражает угловой коэффициент касательной.

2) Записать формулу уравнения касательной.

у =

3) Известно, что угловой коэффициент касательной к графику функции в точке с абсциссой х₀ равен 0,6. Чему равно значение производной в этой точке?

— геометрический смысл.

4) Касательная к графику функции f(x) в точке с абсциссой х₀ образует с положительным направлением оси Ох угол 45 0 . Найдите значение производной в точке касания.

, т.к.

5) В каких точках кривой у = 2 – х 2 касательная к ней параллельна оси Ох.

(0; 2)

6) Какой угол (острый или тупой ) образует с положительным направлением оси Ох касательная к графику функции в точке с абсциссой х₀.

а) — острый.

б) — тупой.

2. Проверка домашней работы.

Двое работают у доски во время устной работы.

3. Работа в группах.

Учитель выступает в роли консультанта. Порядок выполнения заданий не играет роли.

Задача 1. Найти угол между касательными к графику функции , проведенными в точках с абсциссами 1 и 2.

Решение: . Найдем тангенсы углов наклона касательных к положительному направлению оси Ох.

— угол между касательными;

;

;

.

Задача 2. Является ли прямая у=х-1 касательной к кривой у=х 3 -2х+1?

Решение: Найдем общие точки графиков.

Воспользуемся схемой Горнера.

(1;0), (-2;-3) – общие точки.

Найдем угловые коэффициенты касательных в этих точках:

.

k₁= k₂=, т.к. угловой коэффициент прямой у=х-2 равен 1, то в точке (-2;-3) она не может быть касательной.

Найдем уравнение касательной в точке (1;0)

Ответ: у=х-1 – касательная в точке (1;0) к графику функции у= х 3 -2х+1.

Задача 3. На параболе у=х 2 взяты две точки с абсциссами 1 и 3. Через эти точки проведена прямая. В какой точке параболы касательная будет параллельна проведенной прямой?

Решение: у=х 2 , (1;1), (3;9).

Найдем уравнение прямой .

Прямые параллельны, если их угловые коэффициенты равны.

— угловой коэффициент касательной в точке с абсциссой х₀.

2х₀ = 4.

Ответ: в точке (2;4) касательная параллельна заданной прямой.

Задача 4. Составить уравнение касательной к графику функции у=х 3 , х>0, отсекающей от осей координат треугольник, площадь которого равна .

Решение: Пусть (х₀; у(х₀)) — точка касания . Составим уравнение касательной у=х₀ 3 +3х₀ 2 (х-х₀).

Найдем точки пересечения этой прямой с осями координат:

.

А(; 0).

ОВ = 2х₀ 3 ; ОА = .

Sтреуг = ОВ*ОА.

По условию х₀ > 0 х₀ = 1 – абсцисса точки касания.

Уравнение касательной у = 1 3 + 3*1 3 (х – 1).

4. Итог урока.

В – I.

1. Найдите уравнение касательной к графику функции в точке с абсциссой х₀ = — 1.

А) у=-2х-3; Б) у= 2х-1; В) у= -2х+3; Г) у= 2х+3.

2. К графику функции у=3(х+2) проведены две параллельные касательные, одна из которых проходит через точку графика с абсциссой х₀= — 1. Найдите абсциссу точки, в которой другая касательная касается графика данной функции.

А) — 2; Б) 2; В) 1; Г) — 3.

3. Напишите уравнение касательной к графику функции f(x) = x 2 – 4x + 5, если эта касательная проходит через точку (0; 4) и абсцисса точки касания положительна.

А) у = 2х+4; Б) у = -2х+4; В) у = -4х+4; Г) у = 4х-3.

В – II.

1. Найдите уравнение касательной к графику функции в точке с абсциссой х₀ = — 2.

А) у =2х-6; Б) у = 10х+12; В) у= 4х+8; Г) у= -10х+8.

2. К графику функции у=-4(х-3) проведены две параллельные касательные, одна из которых проходит через точку графика с абсциссой х₀= 1. Найдите абсциссу точки, в которой другая касательная касается графика данной функции.

А) — 1; Б) 5; В) 2; Г) — 3.

3. Напишите уравнение касательной к графику функции f(x) = x 2 + 3x + 5, если эта касательная проходит через точку (0; 1) и абсцисса точки касания отрицательна.

А) у = 2х+1; Б) у = х+1; В) у = -х+1; Г) у = -2х-5.

Видео:Касательная к графику функции в точке. 10 класс.Скачать

Составить уравнение касательной, проведенной в точке A ( — 2 ; 1) окружности x ^ 2 + y ^ 2 — 2x + 4y — 13 = 0?

Математика | 10 — 11 классы

Составить уравнение касательной, проведенной в точке A ( — 2 ; 1) окружности x ^ 2 + y ^ 2 — 2x + 4y — 13 = 0.

Составить уравнение касательной, проведенной в точке A ( — 2 ; 1) окружности x ^ 2 + y ^ 2 — 2x + 4y — 13 = 0

( — 2) ^ 2 + 1 ^ 2 — 2( — 2) + 4·1 — 13 = 4 + 1 + 4 + 4 — 13⇒

A ( — 2 ; 1)∈ окружности x ^ 2 + y ^ 2 — 2x + 4y — 13 = 0

(x ^ 2 — 2x) + (y ^ 2 + 4y) — 13 = 0

(x — 1) ^ 2 + (y + 2) ^ 2 = 13 + 1 + 4

(x — 1) ^ 2 + (y + 2) ^ 2 = 18

центр окружности в точке С(1 ; — 2), R = 3√2

т A ( — 2 ; 1) находится на кривой y = √(18 — (x — 1)²)

уравнение касательной y = y0 + f¹( — 2)(x + 2)

f¹(x) = [1 / (2√(18 — (x — 1)²)]·( — 2(x — 1)) = — (x — 1) / √(18 — (x — 1)²) f¹( — 2) = — ( — 2 — 1) / √(18 — ( — 2 — 1)²) = 3 / 3 = 1

уравнение касательной y = 1 + (x + 2) y = x + 3.

Видео:Гипербола и её касательнаяСкачать

Из точки а проведены две касательные к окружности с центром в точке О?

Из точки а проведены две касательные к окружности с центром в точке О.

Из точки а проведены две касательные к окружности с центром в точке О.

Найдите радиус окружности, если угол между касательными равен 60 градусов, а расстояние от точки А до точки О равно 8.

По подробнее пожалуйста.

Видео:Математический анализ, 33 урок, Касательная плоскость и нормаль к поверхностиСкачать

Составить уравнение касательной к окружности х2 + у2 — 4х — 6у + 8 = 0 проведенной в точке А(3 ; 5) на ней?

Составить уравнение касательной к окружности х2 + у2 — 4х — 6у + 8 = 0 проведенной в точке А(3 ; 5) на ней.

Видео:Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

Составить уравнение касательной проведенной к графику функции y = 3x — x ^ 3 в точке с абсциссой x0 = 0?

Составить уравнение касательной проведенной к графику функции y = 3x — x ^ 3 в точке с абсциссой x0 = 0.

Видео:Эллипс, парабола и гипербола. Конические сечения | Ботай со мной #055 | Борис Трушин |Скачать

Составить уровнение касательной к окружности х ^ 2 + y ^ 2 — 4x — 6y + 8 = 0 проведенной в точке на ней А(3 ; 5)?

Составить уровнение касательной к окружности х ^ 2 + y ^ 2 — 4x — 6y + 8 = 0 проведенной в точке на ней А(3 ; 5).

Видео:Составить уравнения касательных к окружности (x-1)2+(y+3)2=40, перпендикулярных прямой 3x+y-4=0Скачать

Угол между касательной и хордой проведенной из точки касания равен 37?

Угол между касательной и хордой проведенной из точки касания равен 37.

Найдите величину дуги высекаемой на окружности этой хордой.

Видео:Уравнение касательной, параллельной заданной прямой.Скачать

Составить уравнение касательной к окружности х2 + у2 — 4х — 6у + 8 = 0, проведенной в точке А(3 ; 5) на ней?

Составить уравнение касательной к окружности х2 + у2 — 4х — 6у + 8 = 0, проведенной в точке А(3 ; 5) на ней.

Видео:§18 Каноническое уравнение эллипсаСкачать

Составить уравнение касательной проведенной к графику функции : f(x) = 2x ^ 2 — x + 1, в точке х0 = 1?

Составить уравнение касательной проведенной к графику функции : f(x) = 2x ^ 2 — x + 1, в точке х0 = 1.

Видео:Лекция. Гиперболоиды, параболоиды, конус. Исследование методом сечений.Скачать

На отрезке Ав выбрана точка С?

На отрезке Ав выбрана точка С.

Построена окружность с центром А проходящая через С.

Найдите длину отрезка касательной проведеной из точки В к этой окружности.

Видео:МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Найдите уравнение касательной, проведенной к графику функции f(x) = sin⁡3x в точке x_0 = π / 6 ?

Найдите уравнение касательной, проведенной к графику функции f(x) = sin⁡3x в точке x_0 = π / 6 .

Найдите уравнение касательной, проведенной к графику функции f(x) = 1 / 4(x ^ 4 + 1) в точке x_0 = 1 .

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Касательной к окружности называется прямая, проходящая через точку окружности?

Касательной к окружности называется прямая, проходящая через точку окружности.

К радиусу, проведенному в эту точка.

Данная точка называется.

Вы перешли к вопросу Составить уравнение касательной, проведенной в точке A ( — 2 ; 1) окружности x ^ 2 + y ^ 2 — 2x + 4y — 13 = 0?. Он относится к категории Математика, для 10 — 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Математика. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

Масса бидона М, его ёмкость V Полный M + 2V = 27 Половина M + V = 15 Вычтем второе из первого V = 12 л И масса бидона M = 15 — V = 3 кг Осталось добавить N литров раствора для того, чтобы масса бидона с раствором была в три раза больше массы пустого ..

1) 500 + 500 = 1000(динаров) получит третий сын. 2) 1000 * 3 = 3000(динаров) всё наследство. 3) 3000 : 2 = 1500(динаров) стоит один дом. Ответ : 1500 (В).

📹 Видео

Обратная пропорциональность. ГИПЕРБОЛА. §10 алгебра 8 классСкачать

Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

§21 Каноническое уравнение гиперболыСкачать