Уравнения и неравенства с модулем графики функций

Видео:Как раскрыть модуль. Неравенство и график с модулем ЕГЭСкачать

Решение неравенств с модулем

Сегодня, друзья, не будет никаких соплей и сантиментов. Вместо них я без лишних вопросов отправлю вас в бой с одним из самых грозных противников в курсе алгебры 8—9 класса.

Да, вы всё правильно поняли: речь идёт о неравенствах с модулем. Мы рассмотрим четыре основных приёма, с помощью которых вы научитесь решать порядка 90% таких задач. А что с остальными 10%? Что ж, о них мы поговорим в отдельном уроке.:)

Однако перед тем, как разбирать какие-то там приёмы, хотелось бы напомнить два факта, которые уже необходимо знать. Иначе вы рискуете вообще не понять материал сегодняшнего урока.

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Что уже нужно знать

Капитан Очевидность как бы намекает, что для решения неравенств с модулем необходимо знать две вещи:

1. Как решаются неравенства;
2. Что такое модуль.

Начнём со второго пункта.

Определение модуля

Тут всё просто. Есть два определения: алгебраическое и графическое. Для начала — алгебраическое:

Определение. — это либо само это число, если оно неотрицательно, либо число, ему противоположное, если исходный $x$ — всё-таки отрицателен.

Записывается это так:

[left| x right|=left ;4 right)$

Задача. Решите неравенство:

[left| ^ >+2x-3 right|+3left( x+1 right) lt 0]

Решение. Это задание уже чуть посложнее. Для начала уединим модуль, перенеся второе слагаемое вправо:

[left| ^ >+2x-3 right| lt -3left( x+1 right)]

Очевидно, перед нами вновь неравенство вида «модуль меньше», поэтому избавляемся от модуля по уже известному алгоритму:

[-left( -3left( x+1 right) right) lt ^ >+2x-3 lt -3left( x+1 right)]

Вот сейчас внимание: кто-то скажет, что я немного извращенец со всеми этими скобками. Но ещё раз напомню, что наша ключевая цель — грамотно решить неравенство и получить ответ. Позже, когда вы в совершенстве освоите всё, о чём рассказано в этом уроке, можете сами извращаться как хотите: раскрывать скобки, вносить минусы и т.д.

А мы для начала просто избавимся от двойного минуса слева:

[-left( -3left( x+1 right) right)=left( -1 right)cdot left( -3 right)cdot left( x+1 right)=3left( x+1 right)]

Теперь раскроем все скобки в двойном неравенстве:

Переходим к двойному неравенству. В этот раз выкладки будут посерьёзнее:

Оба неравенства являются квадратными и решаются методом интервалов (потому и говорю: если не знаете, что это такое, лучше пока не браться за модули). Переходим к уравнению в первом неравенстве:

Как видим, на выходе получилось неполное квадратное уравнение, которое решается элементарно. Теперь разберёмся со вторым неравенством системы. Там придётся применить теорему Виета:

Отмечаем полученные числа на двух параллельных прямых (отдельная для первого неравенства и отдельная для второго):

Опять же, поскольку мы решаем систему неравенств, нас интересует пересечение заштрихованных множеств: $xin left( -5;-2 right)$. Это и есть ответ.

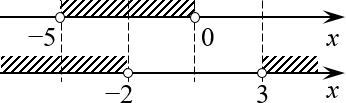
Думаю, после этих примеров схема решения предельно ясна:

1. Уединить модуль, перенеся все другие слагаемые в противоположную часть неравенства. Таким образом мы получим неравенство вида $left| f right| lt g$.
2. Решить это неравенство, избавившись от модуля по описанной выше схеме. В какой-то момент потребуется перейти от двойного неравенства к системе из двух самостоятельных выражений, каждое из которых уже можно решать отдельно.
3. Наконец, останется лишь пересечь решения этих двух самостоятельных выражений — и всё, мы получим окончательный ответ.

Аналогичный алгоритм существует и для неравенств следующего типа, когда модуль больше функции. Однако там есть парочка серьёзных «но». Об этих «но» мы сейчас и поговорим.

Видео:Неравенства с модулем | Математика | TutorOnlineСкачать

2. Неравенства вида «Модуль больше функции»

Выглядят они так:

[left| f right| gt g]

Похоже на предыдущее? Похоже. И тем не менее решаются такие задачи совсем по-другому. Формально схема следующая:

Другими словами, мы рассматриваем два случая:

1. Сначала просто игнорируем модуль — решаем обычное неравенство;
2. Затем по сути раскрываем модуль со знаком «минус», а затем умножаем обе части неравенства на −1, меня при этом знак.

При этом варианты объединены квадратной скобкой, т.е. перед нами совокупность двух требований.

Обратите внимание ещё раз: перед нами не система, а совокупность, поэтому в ответе множества объединяются, а не пересекаются. Это принципиальное отличие от предыдущего пункта!

Вообще, с объединениями и пересечениями у многих учеников сплошная путаница, поэтому давайте разберёмся в этом вопросе раз и навсегда:

• «∪» — это знак объединения. По сути, это стилизованная буква «U», которая пришла к нам из английского языка и является аббревиатурой от «Union», т.е. «Объединения».
• «∩» — это знак пересечения. Эта хрень ниоткуда не пришла, а просто возникла как противопоставление к «∪».

Чтобы ещё проще было запомнить, просто пририсуйте к этим знакам ножки, чтобы получились бокалы (вот только не надо сейчас обвинять меня в пропаганде наркомании и алкоголизма: если вы всерьёз изучаете этот урок, то вы уже наркоман):

Разница между пересечением и объединением множеств

В переводе на русский это означает следующее: объединение (совокупность) включает в себя элементы из обоих множеств, поэтому никак не меньше каждого из них; а вот пересечение (система) включает в себя лишь те элементы, которые одновременно находятся и в первом множестве, и во втором. Поэтому пересечение множеств никогда не бывает больше множеств-исходников.

Так стало понятнее? Вот и отлично. Переходим к практике.

[left| 3x+1 right| gt 5-4x]

Решение. Действуем по схеме:

Решаем каждое неравенство совокупности:

Отмечаем каждое полученное множество на числовой прямой, а затем объединяем их:

Объединение множеств

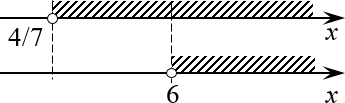
Совершенно очевидно, что ответом будет $xin left( frac ;+infty right)$

Ответ: $xin left( frac ;+infty right)$

Задача. Решите неравенство:

Решение. Ну что? Да ничего — всё то же самое. Переходим от неравенства с модулем к совокупности двух неравенств:

Решаем каждое неравенство. К сожалению, корни там будут не оч:

Во втором неравенстве тоже немного дичи:

Теперь нужно отметить эти числа на двух осях — по одной оси для каждого неравенства. Однако отмечать точки нужно в правильном порядке: чем больше число, тем дальше сдвигам точку вправо.

И вот тут нас ждёт подстава. Если с числами $frac > lt frac > $ всё ясно (слагаемые в числителе первой дроби меньше слагаемых в числителе второй, поэтому сумма тоже меньше), с числами $frac > lt frac > $ тоже не возникнет затруднений (положительное число заведомо больше отрицательного), то вот с последней парочкой всё не так однозначно. Что больше: $frac > $ или $frac > $? От ответа на этот вопрос будет зависеть расстановка точек на числовых прямых и, собственно, ответ.

Поэтому давайте сравнивать:

Мы уединили корень, получили неотрицательные числа с обеих сторон неравенства, поэтому вправе возвести обе стороны в квадрат:

Думаю, тут и ежу понятно, что $4sqrt gt 3$, поэтому $frac > gt frac > $, окончательно точки на осях будут расставлены вот так:

Случай некрасивых корней

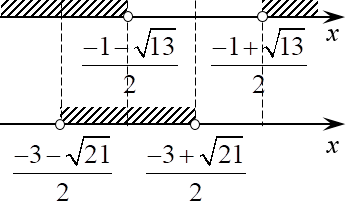
Напомню, мы решаем совокупность, поэтому в ответ пойдёт объединение, а не пересечение заштрихованных множеств.

Как видите, наша схема прекрасно работает как для простых задач, так и для весьма жёстких. Единственное «слабое место» в таком подходе — нужно грамотно сравнивать иррациональные числа (и поверьте: это не только корни). Но вопросам сравнения будет посвящён отдельный (и очень серьёзный урок). А мы идём дальше.

Видео:НЕРАВЕНСТВА С МОДУЛЕМ 😉 ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

3. Неравенства с неотрицательными «хвостами»

Вот мы и добрались до самого интересного. Это неравенства вида:

[left| f right| gt left| g right|]

Вообще говоря, алгоритм, о котором мы сейчас поговорим, верен н только для модуля. Он работает во всех неравенствах, где слева и справа стоят гарантированно неотрицательные выражения:

[f gt g,quad fge 0,gge 0]

Что делать с этими задачами? Просто помните:

В неравенствах с неотрицательными «хвостами» можно возводить обе части в любую натуральную степень. Никаких дополнительных ограничений при этом не возникнет.

Прежде всего нас будет интересовать возведение в квадрат — он сжигает модули и корни:

Вот только не надо путать это с извлечением корня из квадрата:

Бесчисленное множество ошибок было допущено в тот момент, когда ученик забывал ставить модуль! Но это совсем другая история (это как бы иррациональные уравнения), поэтому не будем сейчас в это углубляться. Давайте лучше решим парочку задач:

[left| x+2 right|ge left| 1-2x right|]

Решение. Сразу заметим две вещи:

1. Это нестрогое неравенство. Точки на числовой прямой будут выколоты.
2. Обе стороны неравенства заведомо неотрицательны (это свойство модуля: $left| fleft( x right) right|ge 0$).

Следовательно, можем возвести обе части неравенства в квадрат, чтобы избавиться от модуля и решать задачу обычным методом интервалов:

На последнем шаге я слегка схитрил: поменял последовательность слагаемых, воспользовавшись чётностью модуля (по сути, умножил выражение $1-2x$ на −1).

Дальше можно перенести всё вправо и расписать разность квадратов. Только аккуратно:

Решаем методом интервалов. Переходим от неравенства к уравнению:

Отмечаем найденные корни на числовой прямой. Ещё раз: все точки закрашены, поскольку исходное неравенство — нестрогое!

Избавление от знака модуля

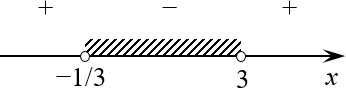
Напомню для особо упоротых: знаки мы берём из последнего неравенства, которое было записано перед переходом к уравнению. И закрашиваем области, требуемые в том же неравенстве. В нашем случае это $left( x-3 right)left( 3x+1 right)le 0$.

Ну вот и всё. Задача решена.

Ответ: $xin left[ -frac ;3 right]$.

Задача. Решите неравенство:

Решение. Делаем всё то же самое. Я не буду комментировать — просто посмотрите на последовательность действий.

Возводим в квадрат:

Всего один корень на числовой прямой:

Ответ — целый интервал

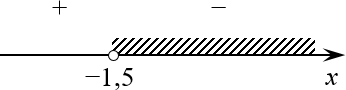
Небольшое замечание насчёт последней задачи. Как точно подметил один мой ученик, оба подмодульных выражения в данном неравенстве заведомо положительны, поэтому знак модуля можно без ущерба для здоровья опустить.

Но это уже совсем другой уровень размышлений и другой подход — его условно можно назвать методом следствий. О нём — в отдельном уроке. А сейчас перейдём к финальной части сегодняшнего урока и рассмотрим универсальный алгоритм, который работает всегда. Даже тогда, когда все предыдущие подходы оказались бессильны.:)

Видео:Решение системы линейных неравенств с одной переменной. 6 класс.Скачать

4. Метод перебора вариантов

А что, если все эти приёмы не помогут? Если неравенство не сводится неотрицательным хвостам, если уединить модуль не получается, если вообще боль-печаль-тоска?

Тогда на сцену выходит «тяжёлая артиллерия» всей математики — метод перебора. Применительно к неравенствам с модулем выглядит он так:

1. Выписать все подмодульные выражения и приравнять их к нулю;
2. Решить полученные уравнения и отметить найденные корни на одной числовой прямой;
3. Прямая разобьётся на несколько участков, внутри которого каждый модуль имеет фиксированный знак и потому однозначно раскрывается;
4. Решить неравенство на каждом таком участке (можно отдельно рассмотреть корни-границы, полученные в пункте 2 — для надёжности). Результаты объединить — это и будет ответ.:)

Ну как? Слабо? Легко! Только долго. Посмотрим на практике:

[left| x+2 right| lt left| x-1 right|+x-frac ]

Решение. Эта хрень не сводится к неравенствам вида $left| f right| lt g$, $left| f right| gt g$ или $left| f right| lt left| g right|$, поэтому действуем напролом.

Выписываем подмодульные выражения, приравниваем их к нулю и находим корни:

Итого у нас два корня, которые разбивают числовую прямую на три участка, внутри которых каждый модуль раскрывается однозначно:

Разбиение числовой прямой нулями подмодульных функций

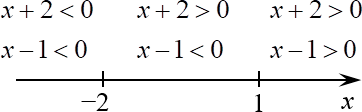
Рассмотрим каждый участок отдельно.

1. Пусть $x lt -2$. Тогда оба подмодульных выражения отрицательны, и исходное неравенство перепишется так:

Получили довольно простое ограничение. Пересечём его с исходным предположением, что $x lt -2$:

Видео:11 класс, 29 урок, Уравнения и неравенства с модулямиСкачать

Уравнения с модулем

Эта статья посвящена приёмам решения различных уравнений и неравенств, содержащих
переменную под знаком модуля.

Если на экзамене вам попадётся уравнение или неравенство с модулем, его можно решить,
вообще не зная никаких специальных методов и пользуясь только определением модуля. Правда,
занять это может часа полтора драгоценного экзаменационного времени.

Поэтому мы и хотим рассказать вам о приёмах, упрощающих решение таких задач.

Прежде всего вспомним, что

Рассмотрим различные типы уравнений с модулем. (К неравенствам перейдём позже.)

Видео:Уравнения с модулем. Разбор 22 задания из ОГЭ | Математика 9 класс | TutorOnlineСкачать

Слева модуль, справа число

Это самый простой случай. Решим уравнение

Есть только два числа, модули которых равны четырём. Это 4 и −4. Следовательно, уравнение
равносильно совокупности двух простых:

Второе уравнение не имеет решений. Решения первого: x = 0 и x = 5.

Видео:Уравнения с модулемСкачать

Переменная как под модулем, так и вне модуля

Здесь приходится раскрывать модуль по определению. . . или соображать!

Уравнение распадается на два случая, в зависимости от знака выражения под модулем.
Другими словами, оно равносильно совокупности двух систем:

Решение первой системы: . У второй системы решений нет.
Ответ: 1.

Первый случай: x ≥ 3. Снимаем модуль:

Число , будучи отрицательным, не удовлетворяет условию x ≥ 3 и потому не является корнем исходного уравнения.

Выясним, удовлетворяет ли данному условию число . Для этого составим разность и определим её знак:

Значит, больше трёх и потому является корнем исходного уравнения

Стало быть, годятся лишь и .

Ответ:

Видео:11 класс, 11 урок, Показательная функция, её свойства и графикСкачать

Квадратные уравнения с заменой |x| = t

Поскольку , удобно сделать замену |x| = t. Получаем:

Видео:Неравенства с модулем Часть 1 из 2 Простейшие неравенстваСкачать

Модуль равен модулю

Речь идёт об уравнениях вида |A| = |B|. Это — подарок судьбы. Никаких раскрытий модуля по определению! Всё просто:

Например, рассмотрим уравнение: . Оно равносильно следующей совокупности:

Остаётся решить каждое из уравнений совокупности и записать ответ.

Видео:Неравенства с модулем Часть 2 из 2 Более сложные неравенстваСкачать

Два или несколько модулей

Не будем возиться с каждым модулем по отдельности и раскрывать его по определению — слишком много получится вариантов. Существует более рациональный способ — метод интервалов.

Выражения под модулями обращаются в нуль в точках x = 1, x = 2 и x = 3. Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении.)

Таким образом, нам нужно рассмотреть четыре случая — когда x находится в каждом из интервалов.

Случай 1: x ≥ 3. Все модули снимаются «с плюсом»:

Полученное значение x = 5 удовлетворяет условию x ≥ 3 и потому является корнем исходного уравнения.

Случай 2: 2 ≤ x ≤ 3. Последний модуль теперь снимается «с минусом»:

Полученное значение x также годится — оно принадлежит рассматриваемому промежутку.

Случай 3: 1 ≤ x ≤ 2. Второй и третий модули снимаются «с минусом»:

Мы получили верное числовое равенство при любом x из рассматриваемого промежутка [1; 2] служат решениями данного уравнения.

Случай 4: x ≤ 1 ≤ 1. Второй и третий модули снимаются «с минусом»:

Ничего нового. Мы и так знаем, что x = 1 является решением.

Видео:МодульСкачать

Модуль в модуле

Начинаем с раскрытия внутреннего модуля.

1) x ≤ 3. Получаем:

Выражение под модулем обращается в нуль при . Данная точка принадлежит рассматриваемому
промежутку. Поэтому приходится разбирать два подслучая.

1.1) Получаем в этом случае:

Это значение x не годится, так как не принадлежит рассматриваемому промежутку.

1.2) . Тогда:

Это значение x также не годится.

Итак, при x ≤ 3 решений нет. Переходим ко второму случаю.

Здесь нам повезло: выражение x + 2 положительно в рассматриваемом промежутке! Поэтому никаких подслучаев уже не будет: модуль снимается «с плюсом»:

Это значение x находится в рассматриваемом промежутке и потому является корнем исходного уравнения.

Так решаются все задачи данного типа — раскрываем вложенные модули по очереди, начиная с внутреннего.

Читайте также о том, как решать неравенства с модулем.

Видео:НЕРАВЕНСТВА С МОДУЛЕМСкачать

Графики функций, содержащих переменную под знаком модуля. Обобщающее повторение при подготовке к экзамену

Разделы: Математика

Определение модуля

Алгебрагическое определение: | x | =

Геометрическое определение: модулем числа называется расстояние от точки, изображающей это число, до начала отсчета.

Понятие модуля впервые вводится в 6 классе, в 7 классе рассматривается линейная функция и ее график и уже можно показывать построение несложных графиков функций, содержащих модуль. Далее, по мере изучения различных функций, их свойств, каждую такую тему можно заканчивать рассмотрением более сложных графиков, в том числе с модулем. В этой статье рассматриваются основные приемы построения графиков таких функций.

I. На алгебрагическом определении основан метод «раскрытия модуля на промежутках».

Например: | x + 2 | = | x + 2 | =

Этот метод можно применять при построении графиков функций, содержащих один или более модулей. Например, построим график функции у = | x + 2 | – 2x + 1 , предварительно упростив ее.

у = у =

Если модулей несколько, то каждый из них раскрываем на промежутках относительно точек, обращающих каждый из них в нуль. Например, построим график функции у = | 3 – x | – x + | x + 2 | + 1.

Функцию записываем как кусочно-заданную:

у =

Подобно тому, как числовая прямая точками – 2 и 3 разбивается на промежутки, координатная плоскость прямыми х = – 2 и х = 3 разбивается на части («полосы»), в каждой из которых строим свой график. Заметим, что данная функция непрерывна, поэтому на «границах» части графика должны соединяться.

II. Этот метод можно применять к функциям разных видов.

Например, построим график функции у = | log₂ x – 1 | – log_0,5 x.

Заметим, что х > 0.

Построим сначала график функции у = х 2 – 2х – 3. Графиком этой функции является парабола, ветви которой направлены вверх. Координаты ее вершины: х = 1, у = – 4. Точки пересечения параболы с осями координат: (0; – 3); (– 1; 0); (3; 0). Далее выполняем отображение части графика, лежащей в нижней полуплоскости, относительно оси абсцисс.

2) у = f(| x |). Используем определение модуля: f(| x |) =

Чтобы построить график такой функции строим график функции у = f(x) и берем ту его часть, где х > 0 (в правой полуплоскости). Затем эту часть симметрично отображаем в левую полуплоскость, где х 2 – 2| х | – 3. Сначала строим график функции у = х 2 – 2х – 3, далее выполняем указанные преобразования.

3) Построим график функции y = | f(| x |)|, например, y = | x 2 – 2| х | – 3 |, выполним последовательно преобразования, рассмотренные в пунктах 2 и 1.

4. Рассмотрим зависимость | y | = f(x). Ее нельзя назвать функцией, так как не выполняется условие: каждому значению х должно соответствовать единственное значение у.

Рассмотрим построение графика такой зависимости (можно говорить «графика уравнения»). Используем определение модуля: у = f(x), если у > 0, – у = f(x), y = – f(x), если у 0; чтобы построить график в нижней полуплоскости (где у 2 – 2х – 3

Заметим, что графики, не относящиеся к рассмотренным частным случаям, следует строить « раскрывая модули на промежутках».

1

0

– 1

y

0

IV. Приведем некоторые примеры

1. Построим график уравнения | y | = arccos| x |.

2. Графическим способом можно решать и неравенства с двумя переменными. Например, решением неравенства | y | 2 – 4 | x | + 3 |; y = + 1.

2. Решите графически уравнения c одной и двумя переменными: | 3 – x | – 3 = 2| x | – x 2 ; | y | = 2| x | – x 2 ; = | x – 2,5 | –1,5.

3. Решите графически неравенства с двумя переменными: | y | > x 2 4x + 3; | x | + | y | 15.11.2011

🔥 Видео

Уравнения с модулем. Часть 2 | Математика | TutorOnlineСкачать

Графическое решение простейших неравенств с модулемСкачать

Математика | Двойной модуль. ОГЭСкачать

Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Неравенства с модулем. Как правильно раскрывать модульСкачать

Решение линейных неравенств, содержащих переменную под знаком модуля. Урок 3.Скачать