Школьная программа не предусматривает выработки прочных навыков решения задач, содержащих параметры, всеми учащимися, и более глубокое изучение возможно только на внеклассных занятиях. Нельзя дать универсальных указаний по решению задач с параметрами. Но для неравенств первой и второй степени с параметрами при заданном условии можно рекомендовать использовать графический метод решения, как более наглядный. При этом учитель может рассмотреть задачи, включающие несколько возможных случаев.
Активному и сознательному усвоению учащимися методов решения неравенств первой и второй степени с параметрами способствует актуализация знаний о свойствах линейной и квадратичной функций и их графиках.
Определение. Функция вида y = kx + b, где k и b – произвольные числа, называется линейной функцией.
Графиком линейной функции является прямая с углом наклона к оси абсцисс равным j , где tg j = k. Если k > 0, то угол j острый; если k j тупой; если k = 0, то график либо совпадает с осью абсцисс, либо параллелен ей.
Задача 1. При каких значениях k неравенство (k – 4)x + k – 5 Ј 3?
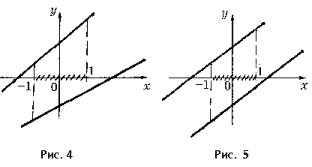
Задача 2. Найти все значения a, при которых для всех x, удовлетворяющих условию | x | Ј 1, справедливо неравенство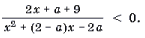 
.
Задача 3. При каких значениях a неравенство 2x – a 2 + 5
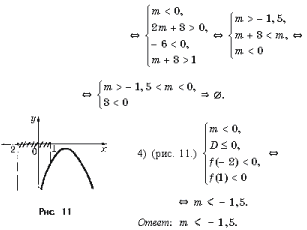
Задача 4. При каких значениях m неравенство (m – 2)x + 2m – 16 і 5?
Задача 5. При каких значениях b неравенство
верно при всех x, удовлетворяющих условию | x | Ј 2?
Неравенства второй степени
Определение. Функция, задаваемая формулой ax 2 + bx + c, где a № 0, называется квадратичной функцией.
График квадратичной функции имеет вид, изображенный на рис. 6, и называется параболой. Точка графика с абсциссой
При a > 0 «ветви» параболы направлены вверх, а при a
При D = b 2 – 4ac > 0 уравнение ax 2 + bx + c = 0 имеет два действительных корня
При D = 0 уравнение имеет один корень
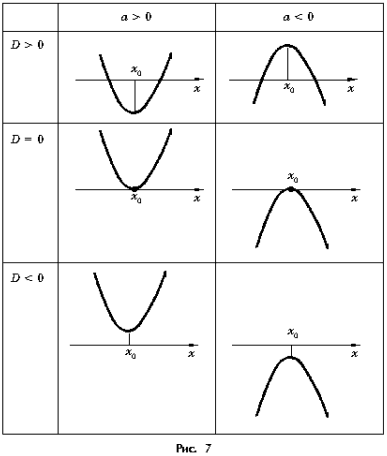
Рассмотрим расположение графика по отношению к оси абсцисс во всех шести случаях (рис. 7).
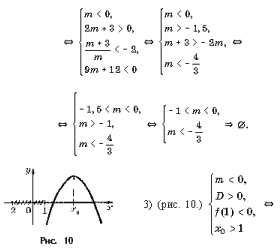
Задача 1. При каких значениях m неравенство mx 2 – 2(m + 3)x + m Ј x Ј 1?
Задача 2. При каких a неравенство ax 2 + 2(3 – 2a)x – 24 > 0 верно при всех x, удовлетворяющих условию | x |
Задача 3. Найдите все значения a, при которых для всех x, удовлетворяющих условию | x | Ј 3, справедливо неравенство
Задача 4. При каких значениях a неравенство ax 2 – x – a(a 2 + 1) > 0 верно при всех x, удовлетворяющих условию | x |
Задача 5. При каких значениях a функция f(x) = – x 3 + 4x 2 – ax – 8 возрастает на (1; 2)?
Решение. Напишем производную от f(x) и воспользуемся критерием возрастания:
f ‘(x) = – 3x 2 + 8x – a > 0, т. е. 3x 2 – 8x + a
Пусть j (x) = 3x 2 – 8x + a. Тогда имеем
Задача 6. Найдите все значения a, при которых функция
Решение задач с параметрами в школьной практике (неравенства – один из видов таких задач) позволяет проверить:
– знание основных разделов школьной математики;
– уровень математического и логического мышления;
– первоначальные навыки исследовательской деятельности;
– перспективы возможности успешного овладения курсом математики вуза.Содержание
- Алгебра
- Целые неравенства
- Неравенства первой степени
- Неравенства второй степени
- Метод интервалов
- Неравенства высоких степеней
- Дробно-рациональные неравенства
- Решение неравенств первой и второй степени с одной переменной
- Описание презентации по отдельным слайдам:
- Математика: теория и методика преподавания в образовательной организации
- Дистанционное обучение как современный формат преподавания
- Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 🔍 Видео
Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать
Алгебра
Помощь студентам в решении контрольных и курсовых работ
Подготовка к дипломной, повышение уникальности
Помощь студентам в решении контрольных и курсовых работ
Консультация, сбор материала, повышение уникальности
Помощь в подготовке дипломной. Сопровождение до защиты!
План урока:
Видео:Решение квадратных неравенств | МатематикаСкачать
Целые неравенства
Неравенства по своей сути очень похожи на уравнения. Аналогично понятию целого уравнения существует понятие целого неравенства. Так называют то нер-во, в котором используются сложение и умножение, вычитание и деление, возведение в степень, но в котором нет деления на выражения с переменной. Другими словами, ни в одном знаменателе в целом нер-ве не должно быть переменных величин.
Приведем примеры целых нер-в:
14х 4 + 13х 2 ⩽ 91х 3 + 2
Если бы переменная могла быть в знаменателе, то знаменатель мог бы обращаться в ноль при некоторых ее значениях, что недопустимо в математике.Но так как в целых нер-вах переменная не находиться в знаменателе, то она может принимать любое значение.
Любое целое нер-во можно преобразовать так, чтобы в одной его части (обычно правой) стоял ноль, а в другой части – некоторый многочлен Р(х).
Пример. Преобразуйте нер-во
(х 3 + 7)(2х – 3) >4х(х 2 – 5х + 9)
к виду Р(х) > 0, где Р(х) – это многочлен.
Решение. Раскроем скобки в каждой части нер-ва:
(х 3 + 7)(2х – 3) >4х(х 2 – 5х + 9)
2х 4 – 3х 3 + 14х – 21 > 4x 3 – 20х 2 + 36х
Перенесем слагаемые влево и приведем подобные слагаемые:
2х 4 – 3х 3 + 14х – 21 – 4x 3 + 20х 2 – 36х > 0
2х 4 – 7х 3 + 20х 2 – 22х – 21 > 0
Ответ:2х 4 – 7х 3 + 20х 2 – 22х – 21 > 0
Как и в случае с уравнениями, у нер-в есть степени. Она равна степени многочлена, стоящего в одной из его частей. Так, степень неравенства в рассмотренном только что примере равна 4, ведь степень полинома 2х 4 – 7х 3 + 20х 2 – 22х – 21 равна 4.
Видео:Как решать неравенства? Часть 1| МатематикаСкачать
Неравенства первой степени
В общем виде неравенства первой степени выглядит так:
где а и b– некоторые числа, а х – переменная.
Естественно, вместо знака «>»могут стоять знаки « 0
Напомним, что решения нер-в традиционно записывают в виде числовых промежутков. Запись х > 3 аналогична записи х∈(3; + ∞). На числовой прямой этот промежуток выглядит так (отмечен штриховкой):
Для наглядности построим график функции у = 5х – 15 и отметим промежуток, на котором она больше нуля:
Заметим, что неравенство строгое, а потому само число 3 в его решение не входит. Из-за этого в записи (3; + ∞) первая скобка – круглая.
Пример. Решите нер-во
х ⩽ 9/(– 3) (обратите внимание, из-за деления на отрицательное число изменился знак нер-ва!)
Также построим график у = – 3х – 9 и убедимся, что мы не ошиблись:
Неравенство нестрогое, и число – 3 входит в ответ, поэтому поле него в промежутке стоит квадратная скобка.
Видео:Решение неравенства методом интерваловСкачать
Неравенства второй степени
Неравенства второй степени в общем виде записываются так:
Примерами таких нер-в являются
5х 2 – 3х + 19 > 0
– 12у 2 + 1,23у + 64 ⩾ 0
462z 2 + 3z– 54 2 + bx + c смотрят вверх, если коэффициент а > 0, и смотрят вниз, если а 2 + bx + c, надо решить квадратное ур-ние ах 2 + bx + c = 0. Если его дискриминант (D) больше нуля, то есть два нуля. Если D = 0, то есть только один ноль. Если D 2 + bx + c> 0
надо решить ур-ние ах 2 + bx + c = 0 и проанализировать положение графика квадратичной функции относительно оси Ох.
Пример. Найдите промежуток, на котором справедливо нер-во
2х 2 – 5х + 2 2 – 5х + 2 = 0.
D = b 2 – 4ас = (– 5) 2 – 4•2•2 = 25 – 16 = 9
Коэффициент а параболы положителен, поэтому ее ветви смотрят вверх. Сам график будет выглядеть так:
Однако нам достаточно и схематичного изображения параболы и ее нулей на координатной прямой:
Нули функции разбивают прямую на три промежутка. На каждом из них знак квадратичной функции неизменен. Отметим эти знаки:
В нер-ве стоит знак « 2 + 9х – 9 ≤ 0
Решение. Сначала находим нули параболы, решая ур-ние
D = b 2 – 4ас = 9 2 – 4•(– 2)•(– 9) = 81 – 72 = 9
Коэффициент а параболы отрицательный, поэтому ее ветви смотрят вниз. Отметим на координатной прямой нули ф-ции и схематично график параболы, а также промежуток, на котором она неположительна:
Так как нер-во нестрогое, то сами нули ф-ции входят в ответ, а потому скобки рядом с нулями – квадратные. В итоге х∊(– ∞; 1,5]∪[3; + ∞).
Пример Решите нер-во
х 2 – 2х + 1 > 0
Решение. Решим квадратное ур-ние
D = b 2 – 4ас = (– 2) 2 – 4•1•1 = 4 – 4 = 0
Дискриминант равен нулю, поэтому у ур-ния лишь 1 корень.
Парабола будет касаться прямой Ох в единственной точке, при этом ветви параболы должны смотреть вверх:
Получается, что ф-ция положительна на всей координатной прямой, кроме точки х = 1, где она обращается в ноль. Соответственно, в ответе надо указать объединение промежутков: х∊(– ∞; 1)∪(1; + ∞).
Пример. Найдите решение нер-ва
– 5х 2 + х – 100 2 + х – 100 = 0
D = b 2 – 4ас = 1 2 – 4•(– 5)•(– 100) = 1 – 2000 = – 2001
Дискриминант меньше нуля, поэтому корней не будет. Вся парабола будет находиться ниже оси Ох, так как ее ветви должны смотреть вниз из-за отрицательного коэффициента а = – 5.
Видно, что при любых значениях х левая часть нер-ва меньше нуля, то есть нер-во справедливо при х∊(– ∞; + ∞).
Видео:Решение квадратных неравенств методом интервалов. 8 класс.Скачать
Метод интервалов
Ясно, что знак произведения зависит от знаков множителей. Так, если мы перемножаем три отрицательных числа и два положительных, то мы получим отрицательное произведение:
Если же отрицательных множителей два или четыре, то итоговое произведение получится положительным:
Вообще можно заметить, что если в произведении находится нечетное количество множителей (1, 3, 5, 7…), то и всё произведение отрицательно. Если же количество отрицательных множителей четно (0, 2, 4, 6, 8…), то произведение положительно. Дело в том, что при умножении отрицательных чисел действует правило «минус на минус дает плюс», то есть два минуса как бы «самоуничтожаются». Поэтому при перемножении четного количества отрицательных чисел все минусы попарно сократятся. Из этого правила есть одно исключение – если хотя бы один множитель равен нулю, то и всё произведение равно нулю, независимо от количества отрицательных сомножителей.
Пример. Справедливо ли нер-во
(– 12)•453•62,36•725•(– 975)•(– 812,99) 0
Перенеся единицу вправо, получим, что
Графически это можно показать так:
Аналогично, рассматривая нер-ва
можно показать, какие значения принимает каждая из скобок при различных х:
Видно, что скобки (х – 1), (х – 2), (х – 3) и (х – 4) изменяют знаки с «–» на «+» при «перескоке» через точки 1, 2, 3 и 4. Отметим их все вместе на одной прямой и укажем знаки скобок на каждом из образовавшихся промежутков:
Получили 5 промежутков. Если выражение выделено красным, то оно отрицательно на промежутке, а если синим – то положительно. Напомним, что произведение отрицательно, если в его состав входит нечетное количество (1, 3, 5…) отрицательных множителей. На рисунке видно, что на промежутке (1; 2) отрицательны 3 множителя, а на промежутке (3; 4) – один множитель. Следовательно, именно на них всё произведение
(х – 1)(х – 2)(х – 3)(х – 4)
оказывается отрицательным. Соответственно на других промежутках произведение положительно. Это можно отметить так:
Штриховкой отмечены промежутки, где произведение отрицательно. Получается, что решением нер-ва является объединение промежутков (1; 2)∪(3; 4). Сами точки 1, 2, 3 и 4 исключены из решения, так как нер-во строгое. Если бы нер-во было нестрогим, то на рисунке точки были бы закрашены, а скобки в промежутке были бы квадратными.
Убедимся в верности этого решения, выбрав произвольное число из каждого промежутка и подставив его в произведение.
Из промежутка (– ∞; 1) возьмем значение х = 0:
(0 – 1)(0 – 2)(0 – 3)(0 – 4) = (– 1)•(– 2)(– 3)•(– 4) = 24 > 0
Из следующего промежутка возьмем х = 1,5:
(1,5 – 1)(1,5 – 2)(1,5 – 3)(1,5 – 4) = 0,5•(– 0,5)•(– 1,5)•(– 2,5) 0
Из промежутка (3; 4) выберем х = 3,5:
(3,5 – 1)(3,5 – 2)(3,5 – 3)(3,5 – 4) = 3,5•1,5•0,5•(– 0,5) 0
Для решения нер-ва мы просто нашли, при каких значениях выражение слева принимает нулевые значения, а потом расставили знаки в полученных интервалах. Данный способ называется методом интервалов.
Пример. Решите неравенство методом интервалов:
(у – 5)(– 2у + 6)(у + 4) ≥0
Решение. Вынесем из второй скобки множитель (– 2):
(у – 5)(– 2)(у – 3)(у + 4) ≥ 0
Поделим нер-во на число (– 2). Напомним, что при делении нер-ва на отрицательную величину его знак меняется на противоположный:
(у – 5)(у – 3)(у + 4) ≤ 0
Используем метод интервалов. Отметим на координатной прямой точки, при которых каждая скобка обращается в ноль (это 5, 3 и (– 4)), и расставим знаки над получившимися промежутками:
Определить эти знаки можно, просто выбрав произвольное число из промежутка и подставив его в левую часть. Так, выберем из промежутка (– ∞; – 4) число (– 5) и получим:
(– 5 – 5)(– 5 – 3)(– 5 + 4) = (– 10)•(– 8)•(– 1) 0
Из промежутка (3; 5) возьмем число 4:
(4 – 5)(4 – 3)(4 + 4) = (– 1)•1•8 0
Итак, выражение слева меньше или равно нулю при у∊(– ∞; – 4]∪[3; 5].
Обратим внимание, что в рассмотренных примерах знаки на промежутках чередовались. Это значит, что достаточно было определить знак на одном промежутке, а дальше просто менять их при переходе через отмеченные точки. Есть один частный случай, когда такое чередование НЕ происходит. Такое возможно, если в двух скобках находится одинаковые выражения.
Пример. Решите нер-во
(z – 5)(3z – 15)(7 – z) ≤ 0
Решение. Вынесем из второй скобки множитель 3, а из третьей – (– 1):
(z – 5)•3•(z – 5)•(– 1)•(z – 7) ≤ 0
Делим нер-во на (– 3):
(z – 5)(z – 5)(z – 7) ≥ 0
Обратите внимание – мы получили две одинаковые скобки (z – 5). Отметим на прямой нули левого выражения (это числа 5 и 7), а также знаки промежутков:
Для расстановки знаков подставим в выражение слева числа:
при z = 4 (4 – 5)(4 – 5)(4 – 7) = (– 1)•(– 1)•(– 3) 0
Получилось, что на соседних интервалах (– ∞; 5) и (5; 7) знаки совпадают, а не чередуются. Так произошло из-за того, что при переходе через точку z = 5 знак поменяла не одна, а сразу 2 скобки (х – 5).
При записи ответа надо учесть, что в задании дано нестрогое нер-во. Поэтому в ответ надо включить как промежуток [7; + ∞), так и число 5, которое обращает в ноль произведение в левой части.
Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать
Неравенства высоких степеней
Напомним, что если некоторое число а – корень многочлена Р(х) (то есть оно является корнем ур-ния Р(х) = 0), то этот многочлен можно представить как произведение двучлена (х – а) и какого-то другого многочлена Р1(х). Другими словами, зная корни многочлена, можно разложить его на множители. За счет этого можно решать нер-ва высоких степеней.
Пример. Решите нер-во
х 3 – 3х 2 – х + 3 3 – 3х 2 – х + 3 = 0
Попробуем подобрать корни, начав с целых чисел. Напомним, что все целые корни должны быть делителем свободного члена, то есть в данном случае числа 3. Поэтому «кандидатами» являются числа 1, (– 1), 3 и (– 3). Подставляя их в ур-ние, находим, что оно имеет три корня: 1, (– 1) и 3:
1 3 – 3•1 2 – 1 + 3 = 1 – 3 – 1 + 3 = 0
(– 1) 3 – 3•(– 1) 2 – (– 1) + 3 = – 1 – 3 + 1 + 3 = 0
3 3 – 3•3 2 – 3 + 3 = 27 – 27 – 3 + 3 = 0
Число (– 3) не подходит, ведь при его подстановке в левую часть ноль не получается:
(– 3) 3 – 3•(– 3) 2 – (– 3) + (– 3) = – 27 +27 + 3 + 3 = 6
Напомним, что у ур-ния 3-ей степени не может быть более 3 корней, поэтому других корней у ур-ния нет.
Зная корни, мы можем разложить многочлен на множители:
х 3 – 3х 2 – х + 3 = (х – 1)(х + 1)(х – 3).
В справедливости такого разложения можно убедиться, раскрыв скобки в правой части этого равенства. Теперь можно переписать исходное нер-во
х 3 – 3х 2 – х + 3 0
при х = 2 имеем (2 – 1)(2 + 1)(2 – 3) = 1•3•(– 1) 0
Получаем, что левая часть отрицательна при х∊(– ∞; – 1)∪(1; 3).
Пример. Решите нер-во
Решение. Рассмотрим ур-ние
Подбором можно определить лишь один его корень – единицу:
Поделим исходный многочлен на (х – 1):
Получили, что х 3 + 2х – 3 = (х – 1)(х 2 + 2х + 3)
Можно ли разложить на множители квадратный трехчлен х 2 + 2х + 3? Попытаемся решить ур-ние
D = b 2 – 4ас = 4 2 – 4•2•3 = 16 – 24 = – 8
Получили, что корней нет. Это значит, что функция у = х 2 + 2х + 3 не пересекает ось Ох, и, так как коэффициент а этого трехчлена положителен, то выражение х 2 + 2х + 3 больше нулю при любом х.
Это можно показать и иначе, если выделить полный квадрат из трехчлена:
х 2 + 2х + 3 = х 2 + 2х + 1 + 2 = (х + 1) 2 + 2
Перепишем исходное нер-во с учетом разложения многочлена на множители:
(х – 1)(х 2 + 2х + 3) > 0
Так как выражение х 2 + 2х + 3 положительно при любом значении х, то мы можем поделить неравенство на него:
Отсюда получаем, что х∊(1; + ∞).
Пример. Укажите наименьшее целое решение неравенства
4х 3 + 4х 2 – 7х + 2 > 0
Решение. Попытаемся найти корень многочлена 4х 3 + 4х 2 – 7х + 2. Целый корень должен быть делителем двойки (свободного члена), то есть возможны варианты 1 и (–1), 2 и (– 2). Из них подходит только – 2:
4•(– 2) 3 + 4•(– 2) 2 – 7•(– 2) + 2 = – 32 + 16 + 14 + 2 = 0
Значит, можно поделить исходный многочлен на х + 2:
Можно записать, что 4х 3 + 4х 2 – 7х + 2 = (х + 2)(4х 2 – 4х + 1).
Далее разложим получившийся при делении квадратный трехчлен на множители, для чего приравняем его к нулю:
D = b 2 – 4ас = (– 4) 2 – 4•4•1 = 16 – 16 = 0
Получается, что есть лишь один корень.
х = – b/(2a) = – (– 4)/(2•4) = 0,5
Если у квадратного трехчлена дискриминант равен нулю, то это значит, что он является полным квадратом какого-то выражения. Действительно:
4х 2 – 4х + 1 = (2х) 2 – 2•2х•1 + 1 2 = (2х – 1) 2
Тогда можно записать:
4х 3 + 4х 2 – 7х + 2 = (х + 2)(4х 2 – 4х + 1) = (х + 2)(2х – 1) 2 =
Перепишем с учетом этого исходное нер-во:
4х 3 + 4х 2 – 7х + 2 > 0
(х + 2)(2х – 1)(2х – 1) > 0
Вынесем множитель 2 из двух последних скобок и поделим нер-во на них:
(х + 2)•2•(х – 0,5)•2•(х – 0,5) > 0
(х + 2)(х – 0,5)(х – 0,5) > 0
Решим его методом интервалов:
Снова из-за двух одинаковых скобок (х – 0,5) на соседних промежутках (– 2; 0,5) и (0,5; 2) получили один и тот же знак. Функция положительна на них, однако она равна нулю при х = 0,5, поэтому это число из решения неравенства исключается. Получаем, что х∈(– 2; 0,5)∪(0,5; + ∞).
Нам надо указать наименьшее целое решение. Самым малым целым числом из множества (– 2; 0,5)∪(0,5; + ∞) является (– 1).
Видео:Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать
Дробно-рациональные неравенства
До сих пор мы рассматривали целые нер-ва. Однако, по аналогии с уравнениями, существуют ещё и дробно-рациональные нер-ва. В них выражение с переменной может стоять в знаменателе. Приведем примеры дробно-рациональных нер-в:
Любое такое нер-во можно представить в виде
где Р(х) и Q(х) – некоторые многочлены. Естественно, вместо знака «>» может стоять и другой знак. Для примера преобразуем к такому виду нер-во
Перенесем все слагаемые влево:
Далее приведем левую часть к общему знаменателю:
Осталось раскрыть скобки:
В итоге и в числителе, и в знаменателе стоят многочлены.
Докажем, что они равносильны друг другу. Возможны 5 случаев:
- И а, и b являются положительными числами. Тогда оба нер-ва верны, ведь и произведение, и отношение двух положительных чисел само положительно:
- Оба числа, а и b, отрицательны, тогда снова оба нер-ва справедливы, ведь при умножении и делении двух отрицательных чисел получается положительное число. Например:
- Только одно из чисел положительно, а другое отрицательно, тогда их произведение, как и частное, меньше нуля, и нер-ва неверны:
(– 10)•5 = – 50 0 и ab> 0 снова одновременно неверны.
Получили, что при любых значениях а и b нер-ва а/b> 0 и ab> 0 либо одновременно справедливы, либо одновременно несправедливы. Это значит, что они равносильны.
Это значит, что от дробно-рационального нер-ва можно перейти к равносильному ему целому нер-ву.
Пример. Решите нер-во
Исходному нер-ву равносильно иное нер-во:
(х – 1)(х – 2)(х – 3)(х – 4)> 0
Решим его методом интервалов:
Получаем, что х∊(1; 2)∪(3; 4).
Пример. Решите нер-во
Решение. В числителе и знаменателе находятся квадратные трехчлены. Их можно разложить на корни, если знать их корни. Найдем их.
D = b 2 – 4ас = (– 9) 2 – 4•1•14 = 84 – 56 = 25
Так как корни равны 2 и 7, то можно записать, что
х 2 – 9х + 14 = (х – 2)(х – 7)
Аналогично разложим знаменатель
х 2 – 14х + 45 = 0
D = b 2 – 4ас = (– 14) 2 – 4•1•45 = 196 – 180 = 16
х 2 – 14х + 45 = (х – 5)(х – 9)
Перепишем исходное нер-во:
Ему равносильно другое нер-во:
(х – 2)(х – 7)(х – 5)(х – 9) > 0
Его можно решить методом интервалов:
Получаем, что х∊(– ∞; 2)∪(5; 7)∪(9; + ∞).
Обратим внимание на одну особенность метода интервала в случаях, когда решается дробно-рациональное нер-во. Она касается нестрогих нер-в (со знаками «≤» и «≥»). В целых нестрогих нер-вах сами точки, при которых выражение слева обращается в ноль, включаются в решение. Но при рассмотрении дроби важно понимать, что ее знаменатель не может быть равным нулю. Поэтому при нестрогом нер-ве в ответ надо включить точки, обращающие в ноль числитель, но при этом исключить точки, обращающие в ноль знаменатель.
Пример. Решите нер-во
Числитель обращается в ноль в точках (– 2) и 4, а знаменатель – в точках (– 7) и 8. Так как нер-во нестрогое, то числа 4 и (– 2) будут входить в решение (на координатной прямой мы отметим их закрашенным кружочком), а числа (– 7) и 8 – нет (их отметим как «выколотые точки»):
В итоге получаем, что дробь неотрицательна при х∊(– ∞; – 7)∪[– 2; 4]∪(8; – ∞).
Видео:Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать
Решение неравенств первой и второй степени с одной переменной
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
Описание презентации по отдельным слайдам:
Решение неравенств первой и второй степени с одной переменной
Неравенства первой степени – это неравенства вида ах + b > 0 или ах + b ≥ 0, ах + b 0; 0,3x +1,2 > 0; 5 – 10x ≤ 0 являются неравенствами первой степени. Решим, например, последнее из этих неравенств: 5 – 10x ≤ 0 x ≥ 0,5 можно считать ответом, так как оно вполне ясно описывает множество всех значений x, являющихся его решениями. Можно также записать решение неравенства в виде числового промежутка: [0,5; +оо). Множеством решений неравенства первой степени всегда является числовой луч
Пример 1. Определим, в каком случае на координатной прямой изображено множество решений неравенства 19 – 7x > 20 – 3(x – 5).
Самая правильная стратегия поиска ответа на вопрос состоит в том, чтобы просто решить неравенство. 19 – 7x > 20 – 3(x – 5), 19 – 7x > 20 – 3x +15, –4x > 16, 4x 0; б) нет корней, а0; г) 1 коре. » onclick=»aa_changeSlideByIndex(5, 0, true)» >
Ответы: у х у х у х у х 0 0 0 0 а) 2 корня, а>0; б) нет корней, а 0; г) 1 корень, а 0 при х (-∞;. » title=»Ответы: у у у х х х 0 0 0 х1 х2 х0 х0 а) у>0 при х (х1;х2), б) у>0 при х (-∞;. » onclick=»aa_changeSlideByIndex(7, 0, true)» >
Ответы: у у у х х х 0 0 0 х1 х2 х0 х0 а) у>0 при х (х1;х2), б) у>0 при х (-∞;+∞), в) у>0 при х (-∞;х0)U(х0;+∞). у 0 и ах2+вх+с 0 2х2-7х 0
Рассмотреть функцию, соответствующую данному неравенству, определить направление ветвей параболы. Найти нули функции, т.е. абсциссы точек пересечения параболы с осью х, если они есть. Изобразить схематически параболу в координатной плоскости. Выбрать нужные промежутки. Записать ответ.
Решить неравенство 5х2+9х-2>0. Решение. у = 5х2+9х-2. Графиком функции является парабола, ветви которой направлены вверх. 2. Нули функции. 5х2+9х-2=0; D=81+40=121, х1=0,2, х2=-2 3. 4. у>0 при х (-∞; -2)U(0,2; +∞). Ответ: (-∞; -2)U(0,2; +∞). -2 0,2 х у 0
Решите неравенство: Вариант 1 Вариант 2 а) х²-9>0; а) х²-16 0; в) –х²-10х-25>0. в) –х²+6х-9>0.
Правильные ответы: Вариант 1 Вариант 2 а) (-∞;-3)U(3;+∞); а) (-4;4); б) (3;5); б) (-∞;3)U(7;+∞); в) решений нет. в) решений нет.
Спасибо за урок!
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 694 человека из 75 регионов
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 867 человек из 78 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Сейчас обучается 52 человека из 24 регионов
«Профессиональный имидж педагога: стереотипы и методы их преодоления»
Свидетельство и скидка на обучение каждому участнику
«Мотивация здорового образа жизни. Организация секций»
Свидетельство и скидка на обучение каждому участнику
- Для всех учеников 1-11 классов
и дошкольников- Интересные задания
по 16 предметам
Видео:Неравенства с двумя переменными. 9 класс.Скачать
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 840 320 материалов в базе
Материал подходит для УМК
«Алгебра», Никольский С.М., Потапов М.К., Решетников Н.Н. и др.
§ 2. Неравенства второй степени с одним неизвестным
Ищем педагогов в команду «Инфоурок»
Другие материалы
- 17.10.2020
- 990
- 40
- 16.10.2020
- 442
- 57
- 04.08.2020
- 634
- 39
- 27.07.2020
- 97
- 0
- 26.07.2020
- 201
- 11
- 20.07.2020
- 343
- 35
- 18.07.2020
- 162
- 14
- 03.07.2020
- 1170
- 102
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 18.10.2020 616
- PPTX 2.1 мбайт
- 11 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Луценко Елена Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 6 месяцев
- Подписчики: 1
- Всего просмотров: 20502
- Всего материалов: 11
Московский институт профессиональной
переподготовки и повышения
квалификации педагоговВидео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать
Дистанционные курсы
для педагогов663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
С 1 сентября в российских школах будут исполнять гимн России
Время чтения: 1 минута
Около 20% детей до 15 лет не воспринимают прочитанную информацию
Время чтения: 1 минута
Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу
Время чтения: 1 минута
Минобрнауки отменило плановые и внеплановые проверки вузов в 2022 году
Время чтения: 1 минута
Эвакуированные в Россию из ДНР и ЛНР дети смогут поступить в вузы по квоте
Время чтения: 1 минута
Онлайн-конференция о профессиональном имидже педагога
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
🔍 Видео
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать
Решение неравенств второй степени с одной переменной. Алгебра, 9 классСкачать
Понятие неравенства второй степени с одним неизвестным.Скачать
Решение неравенств второй степени. Видеоурок 12. Алгебра 9 классСкачать
Алгебра 9. Урок 1 - Неравенства. Определения и свойстваСкачать
Алгебра 9. Урок 7 - Неравенства. Метод интервалов - основные фактыСкачать
Решение системы неравенствСкачать
Это просто! Как решать Показательные Неравенства?Скачать
Алгебра 9 класс (Урок№19 - Решение неравенств второй степени с одной переменной.)Скачать
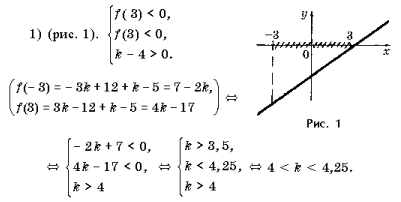
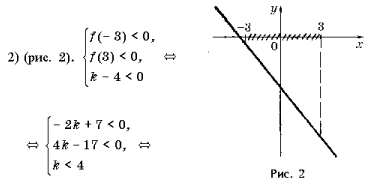
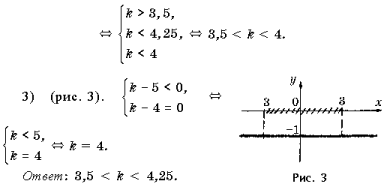
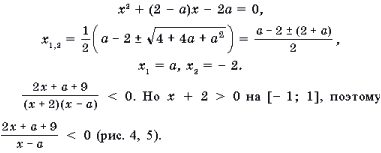
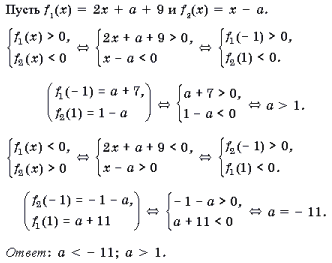
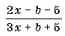верно при всех x, удовлетворяющих условию | x | Ј 2?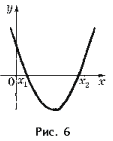
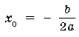называется вершиной параболы, ордината этой точки равна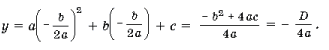
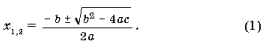
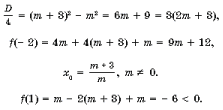
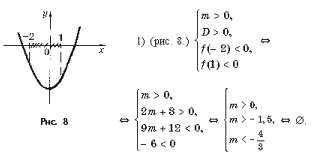
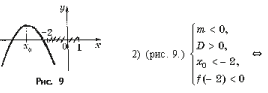
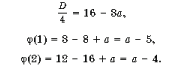
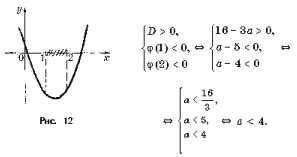
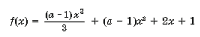возрастает для всех x О R.
