Чтобы уметь решать различные задачи на движение тел по физике, необходимо знать определения физических величин, а также формулы, с помощью которых они связаны. В этой статье будут рассмотрены вопросы, что такое тангенциальная скорость, что такое полное ускорение и какие компоненты его составляют.
- Понятие о скорости
- Понятие об ускорении
- Полное, нормальное и тангенциальное ускорения
- Связь тангенциального ускорения и скорости
- Скорость и нормальное ускорение
- § 1.27. Тангенциальное, нормальное и полное ускорения
- Ускорение при неравномерном криволинейном движении
- Модуль нормального ускорения
- Модуль тангенциального и полного ускорений
- Классификация движений
- Тангенциальное ускорение — определение, формула и измерение
- Общие сведения
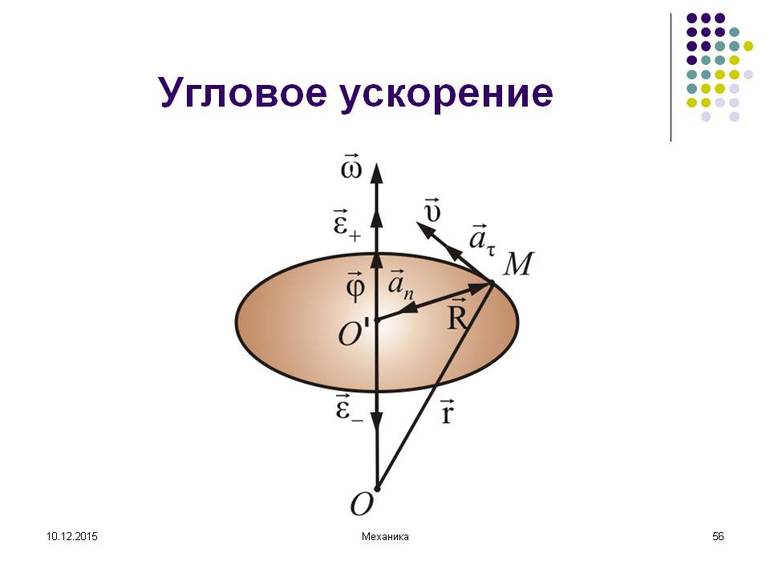
- Угловое ускорение
- Вывод формулы
- Решение простых примеров
- Сложная задача
- 🎦 Видео
Видео:Лекция 6.5 | Нормальное и тангенциальное ускорение | Александр Чирцов | ЛекториумСкачать

Понятие о скорости
Двумя основными величинами кинематики перемещения тел в пространстве являются скорость и ускорение. Скорость описывает быстроту перемещения, поэтому математическая форма записи для нее имеет следующий вид:

Здесь l¯ — является вектором перемещения. Иными словами, скорость — это производная по времени от пройденного пути.
Как известно, всякое тело движется по воображаемой линии, которая называется траекторией. Вектор скорости всегда направлен по касательной к этой траектории, в какой бы точке не находилось движущееся тело.
Существует несколько названий величины v¯, если рассматривать ее совместно с траекторией. Так, поскольку направлена она по касательной, то ее называют тангенциальной скоростью. Также о ней могут говорить, как о линейной физической величине в противоположность угловой скорости.
Вычисляется скорость в метрах в секунду в СИ, однако на практике часто пользуются километрами в час.
Видео:Рассмотрение темы: "Тангенциальное, нормальное и полное ускорение"Скачать
Понятие об ускорении
В отличие от скорости, которая характеризует быстроту прохождения телом траектории, ускорение — это величина, описывающая быстроту изменения скорости, что математически записывается так:
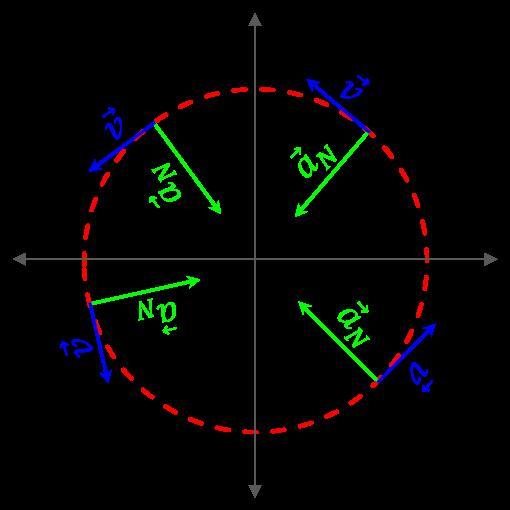
Как и скорость, ускорение — это векторная характеристика. Однако его направление не связано с вектором скорости. Оно определяется изменением направления v¯. Если в процессе движения скорость не изменяет своего вектора, тогда ускорение a¯ будет направлено вдоль той же линии, что и скорость. Такое ускорение называют тангенциальным. Если же скорость будет менять направление, сохраняя при этом абсолютное значение, то ускорение будет направлено к центру кривизны траектории. Оно называется нормальным.
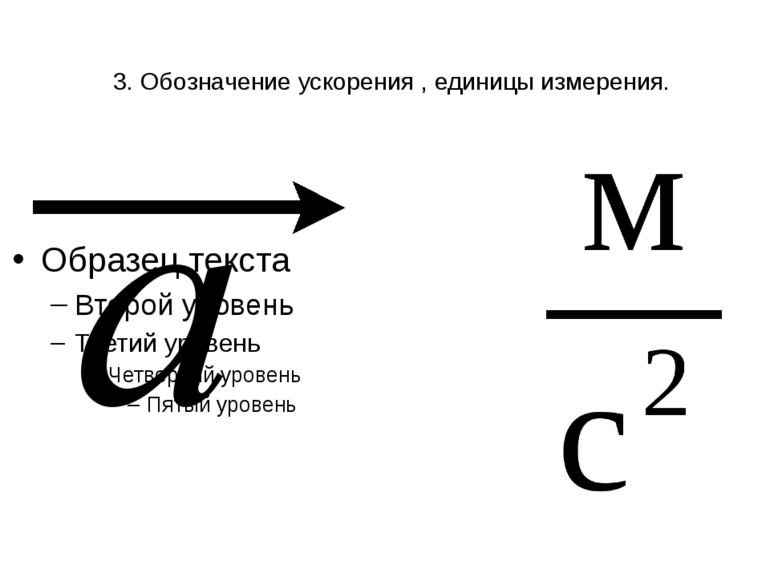
Измеряется ускорение в м/с2. Например, известное всем ускорение свободного падения является тангенциальным при вертикальном подъеме или падении объекта. Его величина вблизи поверхности нашей планеты составляет 9,81 м/с2, то есть за каждую секунду падения скорость тела увеличивается на 9,81 м/с.
Причиной появления ускорения является не скорость, а сила. Если сила F оказывает действие на тело массой m, то она неминуемо создаст ускорение a, которое можно вычислить так:
Эта формула является прямым следствием из второго закона Ньютона.
Видео:Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

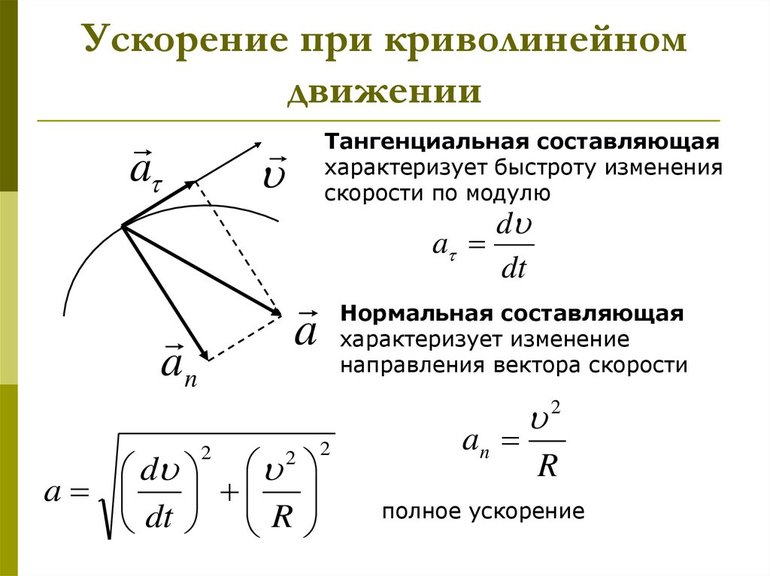
Полное, нормальное и тангенциальное ускорения
Скорость и ускорение как физические величины были рассмотрены в предыдущих пунктах. Теперь мы подробнее изучим, какие компоненты составляют полное ускорение a¯.
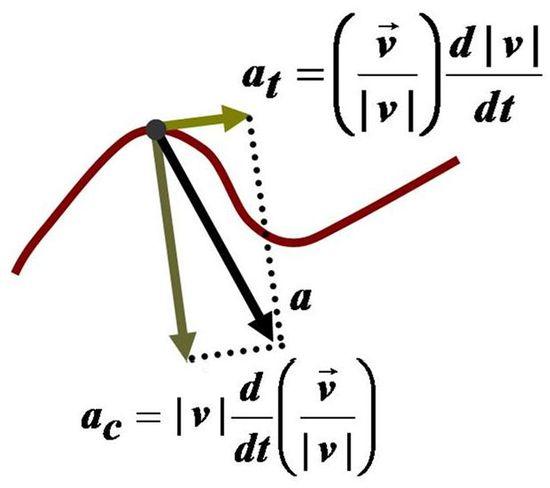
Предположим, что тело движется со скоростью v¯ по криволинейной траектории. Тогда будет справедливо равенство:
Вектор u¯ имеет единичную длину и направлен вдоль касательной линии к траектории. Воспользовавшись таким представлением скорости v¯, получим равенство для полного ускорения:
a¯ = dv¯/dt = d(v*u¯)/dt = dv/dt*u¯ + v*du¯/dt.
Полученное в правом равенстве первое слагаемое называется тангенциальным ускорением. Скорость связана с ним тем фактом, что она количественно определяет изменение абсолютного значения величины v¯, не принимая во внимание ее направление.
Второе слагаемое — это нормальное ускорение. Оно количественно описывает изменение вектора скорости, не принимая во внимание изменение ее модуля.
Если обозначить как at и an тангенциальную и нормальную составляющие полного ускорения a, тогда модуль последнего можно вычислить по формуле:
Видео:Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

Связь тангенциального ускорения и скорости
Соответствующую связь описывают кинематические выражения. Например, в случае движения по прямой с постоянным ускорением, которое является тангенциальным (нормальная составляющая равна нулю), справедливы выражения:
В случае движения по окружности с постоянным ускорением эти формулы так же справедливы.
Таким образом, какой бы ни была траектория перемещения тела, тангенциальное ускорение через тангенциальную скорость рассчитывается, как производная по времени от ее модуля, то есть:
Например, если скорость изменяется по закону v = 3*t3 + 4*t, тогда at будет равно:
at = dv/dt = 9*t2 + 4.
Видео:Хитрый способ нахождения тангенциального и нормального ускорений: Волькенштейн 1.19Скачать

Скорость и нормальное ускорение
Запишем в явном виде формулу для нормальной компоненты an, имеем:
an¯ = v*du¯/dt = v*du¯/dl*dl/dt = v2/r*re¯
Где re¯ — единичной длины вектор, который к центру кривизны траектории направлен. Это выражение устанавливает связь тангенциальной скорости и нормального ускорения. Видим, что последнее зависит от модуля v в данный момент времени и от радиуса кривизны r.
Нормальное ускорение появляется всегда, когда изменяется вектор скорости, однако оно равно нулю, если этот вектор сохраняет направление. Говорить о величине an¯ имеет смысл только тогда, когда кривизна траектории является конечной величиной.
Выше мы отмечали, что при движении по прямой линии нормальное ускорение отсутствует. Однако в природе существует тип траектории, при движении по которой an имеет конечную величину, а at = 0 при |v¯| = const. Этой траекторией является окружность. Например, вращение с постоянной частотой металлического вала, карусели или планеты вокруг собственной оси происходит с постоянным нормальным ускорением an и нулевым тангенциальным ускорением at.
Видео:Центростремительное ускорение. 9 класс.Скачать

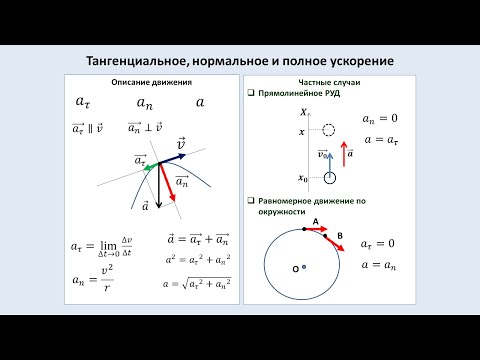
§ 1.27. Тангенциальное, нормальное и полное ускорения
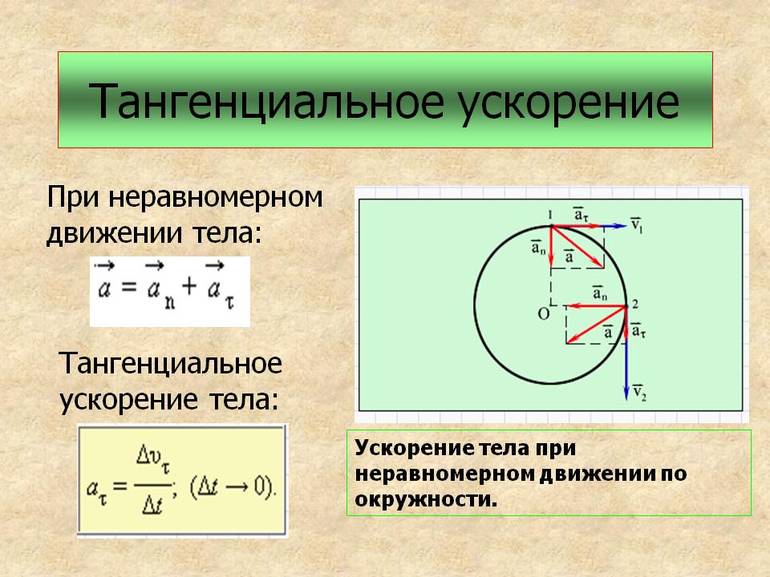
Ускорение при неравномерном криволинейном движении
Пусть в некоторый момент времени t точка занимает положение А (рис. 1.83, а) и имеет скорость v1, a спустя малое время Δt точка переместилась в положение В1 приобретя скорость v2.
Разложим вектор изменения скорости Δ 








Δ 


Разделим почленно это равенство на Δt и перейдем к пределу при стремлении Δt -» 0:
Каждое слагаемое этого равенства есть составляющая ускорения (см. § 1.15). Левая часть равенства (1.27.1) является полным ускорением точки. Первое слагаемое в правой части называется тангенциальным (касательным) ускорением, второе слагаемое — уже знакомое нам нормальное ускорение.
Тангенциальное ускорение направлено по касательной к траектории, так как 

Полное ускорение точки равно сумме тангенциального и нормального ускорений:
На рисунке 1.84, а изображен случай ускоренного движения, а на рисунке 1.84, б — замедленного движения точки.
Модуль нормального ускорения
Мы нашли, как направлены тангенциальное и нормальное ускорения. Выражение для модуля нормального ускорения при движении по окружности радиусом r нам известно:
Если движение происходит вдоль произвольной кривой, то под r надо понимать радиус кривизны траектории в данной точке. Выясним, что такое радиус кривизны кривой линии в точке. Выберем на кривой АВ вблизи точки М с обеих сторон от нее еще две точки: К и L (рис. 1.85). Через три точки К, М и L можно провести единственную окружность. Если точки К и L приближать к точке М, каждый раз проводя через эти три точки окружность, то мы получим серию окружностей разных радиусов, дуги которых вблизи точки М все меньше и меньше будут отличаться от кривой АВ.
В пределе, когда точки К и L сколь угодно близко подходят к точке М, радиус проходящей через них окружности также стремится к предельному значению. Это предельное значение радиусов окружностей и называется радиусом кривизны кривой АВ в точке М.
Модуль тангенциального и полного ускорений
Модуль тангенциального ускорения равен
где dv — приращение модуля скорости за бесконечно малый интервал времени dt. Модуль полного ускорения а. точки можно найти по теореме Пифагора (см. рис. 1.84, а, б):
Полное ускорение направлено по секущей в сторону вогнутости траектории.
Классификация движений
По значениям, которые принимают нормальное и тангенциальное ускорения, можно классифицировать различные движения точки.
Если аn = 0, то при любых значениях скорости движение точки происходит по прямой линии. Эту прямую можно рассматривать как окружность бесконечно большого радиуса (г —> ∞).
Если аt = 0 и аn = 0, но скорость отлична от нуля, то движение по прямой будет равномерным, так как не меняется модуль скорости.
В случае аn ≠ 0 движение точки криволинейное, так как меняется направление скорости. Когда аn ≠ 0, аt = 0, то при движении по кривой линии модуль скорости точки не изменяется — точка движется равномерно.
Если аt = 0, аn = const, то точка совершает равномерное движение по окружности.
И наконец, когда оба ускорения 

В заключение заметим, что если точка движется равномерно по криволинейной траектории, то можно вычислить путь, пройденный точкой, по формуле s = vt.
При произвольном движении вектор ускорения направлен внутрь траектории. Тангенциальная составляющая этого вектора характеризует изменение скорости по модулю, а нормальная составляющая — по направлению.
Видео:Нормальное и тангенциальное ускорение [Физзадачи #37]Скачать
![Нормальное и тангенциальное ускорение [Физзадачи #37]](https://i.ytimg.com/vi/HTVGtCaQgEk/0.jpg)
Тангенциальное ускорение — определение, формула и измерение
Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Общие сведения
Первая лекция для студентов, изучающих кинематику, начинается с рассмотрения тангенциального ускорения, характеризуемого произвольным движением. По сути, рассматривается неравномерное прямолинейное движение общего вида. Кинематика входит в механику и изучает перемещение объектов без учёта сил, вызвавших их движение. Под перемещением понимают изменение положения в пространстве по отношению к другому физическому телу, которое и считается точкой отсчёта. Если изменение положения связать с координатами и временем, то образуется система отсчёта. С её помощью можно определить положение объекта в любой момент.
В кинематике любые процессы принято рассматривать, приняв тело за материальную точку. То есть его размерами и формой пренебрегают. При изменении за какой-то промежуток времени точка проходит путь, описывающийся линией — траекторией. Она является скалярной величиной, а само перемещение — векторной. Движение материальной точки может происходить с разной скоростью и ускорением. Быстроту движения разделяют на среднюю и мгновенную. Вторая определяется как предел, к которому стремится скорость на бесконечно малом временном интервале: v = Δs / Δt (Δt → 0).
Перемещение может происходить с ускорением. Это физическая величина, определяющая изменение быстроты перемещения. Иными словами, показывает изменение положения за единицу времени. Измеряется она в метрах на секунду в квадрате. В кинематике существует три вида ускорения:
- Тангенциальное — направленное вдоль касательного пути точки в определённый момент. Из-за происхождения слова его часто называют касательным.
- Нормальное — совпадающее с нормалью траектории изменения положения.
- Полное — определяющееся суммой тангенциального и нормального ускорений.
Но также используется понятие «вектор среднего ускорения тела». Определяется он как приращение вектора скорости за промежуток времени: aср = Δv / Δt. При этом он будет совпадать по направлению с вектором скорости, то есть направлен в сторону вогнутости траектории.
Видео:Вращательное движение. 10 класс.Скачать

Угловое ускорение
Если имеется какая-то точка, находящаяся на вращающемся теле, то скорость её направлена по касательной. Когда движение равномерное, то линейная скорость связана с угловой равенством: v = w * r. А вот ускорение тела будет направлено по радиусу к центру окружности, причём модуль вычисляется как a = v / r либо если это точка на вращающемся теле: a = w2 * r.
В момент, когда тело поворачивается за небольшой промежуток времени на угол дельта фи, угловую скорость можно связать с условием поворота через формулу: w = Δ φ / Δ t. Если тело вращается равномерно, то промежуток времени может быть любым. В ином случае эта величина будет равна мгновенной угловой скорости.
Можно представить, что материальная точка движется неравномерно, то есть изменяется угловая скорость тела. Линейная скорость не будет представлять собой постоянную величину, в отличие от равномерного перемещения. Угол поворота равняется: w = v / r. Так как скорость не может быть константой, то отсюда следует, что и угловая скорость не будет постоянной величиной. Её изменение обозначают Δw. Она равняется разности конечной угловой скорости и начальной: Δw = wк — wн.
Изменение угловой скорости можно разделить на промежуток времени, за который оно поменяло значение: (wк — wн) / Δt. По сути, получается ускорение. Обозначается характеристика буквой эпсилон E и называется угловым ускорением. Измеряется характеристика в радианах на секунду в квадрате. Её смысл заключается в описании физической величины через отношение изменения угловой скорости тела за небольшой промежуток времени к длительности этого промежутка.
Пусть есть дуга окружности с центром. В начальный момент времени у тела есть скорость, направленная по касательной к траектории v0. Через некоторое время точка переместится по окружности на небольшое расстояние. Так как движение неравномерное, модуль скорости изменится v ≠ v0. Для того чтобы найти ускорение тела, нужно воспользоваться следующей формулой: a = Δv / Δt, при этом Δv = v — v0.
Чтобы найти эту разность, нужно воспользоваться правилом треугольника. Для этого следует перенести вектор V0 к V и соединить их линией. Радиус от центра к материальной точке можно обозначить R. Дельта V можно представить, как сумму взаимно перпендикулярных векторов. Один из них будет направленных тангенциально к радиусу, в физике обозначают его Δ Vτ, а другой радиально Δ Vr. В итоге: ΔV = Δ Vτ + Δ Vr.
Видео:Лекция №1 "Кинематика материальной точки" (Булыгин В.С.)Скачать

Вывод формулы
Для доказательства формулы необходимо рассмотреть плоскую систему координат, в которой материальная точка изменяет своё положение по криволинейной траектории. В начальный момент её скорость будет равняться V0. Через некоторое время она изменится и станет V. На графике в плоском измерении это можно представить в виде синусоиды. В определённый момент времени скорость превышает начальную: V > V0. На схеме вектор нулевой скорости направлен из точки t0 вверх по касательной, а вектор V с нижней точки синусоиды параллельно оси ординаты.
Исходя из графика, можно сделать два вывода:
- Через промежуток времени Δt скорость изменяется как по направлению, так и по модулю: Δt = t — t0.
- Вектор изменения скорости, определяемый по правилу треугольника, будет равняться разности существующей скорости на данный момент и начальной: Δv = v — v0.
Для того чтобы построить вектор изменения Δv, нужно из конечной точки отрезка V0 провести линию к рассматриваемой точки, характеризующейся во времени скоростью V. Вершины полученного треугольника можно обозначить буквами ABD. Из верхнего угла B на сторону AD можно опустить медиану. Точка пересечения со стороной пусть будет C. Получается, что вектор Δv можно разложить на две составляющие — отрезки BC и СD. Причём медиана равняется Δvn, а изменение по оси ординаты Δvt.
Для разложения необходимо использовать вектор АС, длина которого совпадает с Vo по модулю: |AC| = |AB| = V0. Так как Δvn — результирующий вектор, то его можно вычислить через сумму: Δv = Δvn + Δvt. Причём первый член в равенстве характеризует изменение быстроты за промежуток времени по направлению, а второй — по модулю. Исходя из того, что t не равняется нулю, на него можно разделить левую и правую часть равенства: Δv / Δt = Δvn / Δt + Δvt / Δt. Если дельта-времени стремится к нулю, то формулу можно переписать в виде: lim Δv / Δt = lim Δvn / Δt + lim Δvt / Δt.
Учитывая связь между ускорениями и то, что полное значение состоит из суммы изменения быстроты движения по модулю и направлению, можно утверждать о верности формулы: a = at + an. Так как направление векторов ускорения и скорости всегда совпадают, то последний можно представить, как параметр, состоящий из двух взаимно перпендикулярных компонент:
- at — тангенциальной составляющей, совпадающей с отрезком V;
- an — перпендикулярным по отношению расположения V вектором.
Используя теорему Пифагора, можно сказать, что модуль полного ускорения равняется корню квадратному из суммы квадратов тангенциального и нормального ускорения: a = √at 2 + an 2 .
Видео:Что такое тангенциальное ускорение #shorts #ЕНТ #ЕНТ_по_физике #Умскул #НиколайАкуловСкачать

Решение простых примеров
В школьном курсе на уроках физики учащимся для закрепления материала предлагается решить определённый тип задач, используя определение тангенциального ускорения. Это типовые примеры, объясняющие суть характеристики и её применение в реальной практике. Вот некоторые из них.
- Вычислить все ускорения точки, лежащей на окружности, через десять секунд после воздействия на диск вращателя. При этом учесть, что радиус окружности составит 20 см, а угол между валом и радиус вектором тела соответствует закону: j =3-t+0.2t 3 . Для решения примера необходимо использовать формулы для нахождения угловой скорости и ускорения. Подставив заданные значения, можно получить: w = d φ / dt = -1 + 0,2 * 3t 2 и e = dw / dt = 0,6 * 2t. Применив формулу связи, легко найти ускорение: at = R * E * (0,6 * 2t) = 1,2 * Rt = 24 м 2 /с. Подставив в формулу нормального ускорения значения, можно вычислить и его an = V 2 / R = R * (0,6 * 10 2 — 1) 2 / 0,2 = 696 м/с 2 . Отсюда полное ускорение будет равняться: a = √ 24 2 + 696 2 = 697 м/с 2 .
- Материальное тело перемещается по окружности, имеющей радиус 20 см. При этом тангенциальное ускорение равняется 5 см на секунду в квадрате. Определить, сколько понадобится времени, чтобы ускорения сравнялись и нормальное стало больше тангенциального в два раза. Исходя из условия, можно утверждать, что движение является равноускоренным. Поэтому можно применить формулы: an = V2 / t; at = V / t. Отсюда: t = V / at, а V = √an * R. Подставив второе выражение в первое, получится: t = (√an * R) / at. При равенстве ускорений an = at, будет верной запись: t = √R / at = √20 / 5 = 2 с. Для второго случая an = 2at, поэтому: t = (√2 * 20) / 5 = 2,8 c.
Но не всегда решаемые задания можно решить, обойдясь одной формулой. При этом значения тех или иных величин могут быть довольно сложными для проведения вычислений. В таких случаях есть резон использовать так называемые онлайн-калькуляторы. Это специализированные сайты, выполняющие подсчёт в автоматическом режиме. Из таких сервисов можно выделить: сalc, widgety, webmath. Указанные интернет-решители работают на русском языке, так что вопросов, как с их помощью выполнять расчёты, возникнуть не должно.
Видео:Нормальное и тангенциальное ускорениеСкачать

Сложная задача
Пусть имеется физическое тело, которое движется, замедляясь по окружности радиусом R так, что в каждый момент времени её тангенциальное и нормальное убыстрение равны друг другу по модулю. Необходимо найти зависимость скорости и полного ускорения от времени и пройденного пути. В начальный момент скорость равняется V0.
Согласно условию, тангенциальное ускорение будет отрицательным, так как точка движется, замедляясь. Для понимания задачи можно изобразить схему движения. Для этого необходимо нарисовать окружность и указать на ней вектор начальной скорости, тангенциального и нормального ускорения. Изобразить вектор полного ускорения как сумму векторов.
Нормальное ускорение можно выразить через скорость и радиус: an = V 2 / R. Затем необходимо записать формулу для тангенциального ускорения: at = dV / dt. Так как они равны, то справедливым будет равенство: V 2 / R = dV / dt. Анализируя уравнение, можно сделать вывод, что так как скорость и радиус положительный, то слева будет стоять величина со знаком плюс. Но, с другой стороны, со временем скорость убывает, поэтому с правой стороны нужно поставить знак минус: V 2 / R = — dV / dt.
Полученное уравнение является дифференциальным и показывает зависимость скорости от времени. Равенство можно преобразовать, умножив на отношение dt / V 2 . В итоге должно получиться выражение: dV / V 2 = — dt / R. Это уравнение можно проинтегрировать. При этом пределами интеграла с левой стороны будет V0 и V, а с правой — 0 и t. Получился обыкновенный степенной интеграл, который будет равняться: 1 / V = dt / R.
Подставив пределы, можно получить равенство: (1 / V) — (1 / V0) = t / R. Из полученной формулы следует выразить скорость: V = (V0 * R) / (R + V0 * t). Поделив числитель и знаменатель на радиус, ответ примет вид: V (t) = V0 / (1 + (V0 * t / R)).
Теперь можно найти тангенциальное убыстрение, так как оно представляет производную от скорости. После взятия производной получится: at = dV / dt = — V02 / R (1 + V0 * t / R)2 = — V2 / R. Отсюда можно написать, что модуль полного ускорения будет равняться: a = √2 *|ar| = (√2 * V2) / R. Осталось найти путь. Он совпадает с длиной дуг и равняется интегралу модуля скорости от времени. После решения должно получиться равенство: S (t) = R * ln (1 + V0 * t / R). Задача решена.
🎦 Видео
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Найти нормальное и тангенциальное ускорения движения через 3 секунды после начала движенияСкачать

Траектория и уравнения движения точки. Задача 1Скачать

Скорости и ускорения точек вращающегося телаСкачать

Кинематика точки. Продолжение. Авторы: Борисов Никита, Ларионов Егор, Петрашова ПолинаСкачать

Физика - движение по окружностиСкачать

Координаты тела заданы параметрически. Найти скорость, тангенциальное и нормальное ускоренияСкачать

Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать