 Линейная функция Линейная функция |
 График линейной функции График линейной функции |
 Прямые, параллельные оси ординат Прямые, параллельные оси ординат |
 Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые |
- Линейная функция
- График линейной функции
- Прямые, параллельные оси ординат
- Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
- График линейной функции, его свойства и формулы
- Понятие функции
- Понятие линейной функции
- Свойства линейной функции
- Построение линейной функции
- Решение задач на линейную функцию
- 4.13. Уравнения прямых на координатной плоскости
- 🎥 Видео
Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Линейная функция
Линейной функцией называют функцию, заданную формулой
| y = kx + b, | (1) |
где k и b – произвольные (вещественные) числа.
При любых значениях k и b графиком линейной функции является прямая линия .
Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .
Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

График линейной функции
При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.
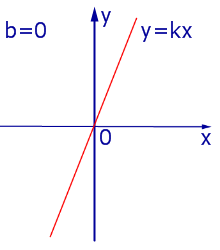 |
| Рис.1 |
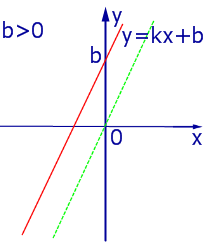 |
| Рис.2 |
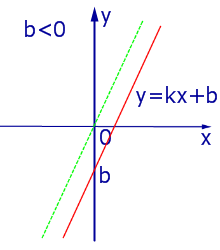 |
| Рис.3 |
При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.
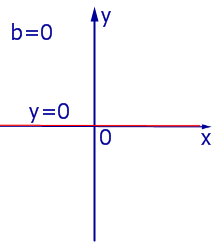 |
| Рис.4 |
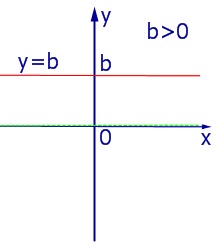 |
| Рис.5 |
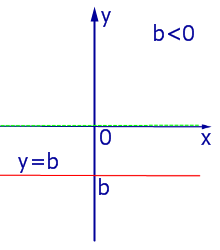 |
| Рис.6 |
При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.
| k y = kx + b1 и y = kx + b2 , имеющие одинаковые угловые коэффициенты и разные свободные члены имеющие разные угловые коэффициенты y = kx + b1 и перпендикулярны при любых значениях свободных членов. Угловой коэффициент прямой линии
равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).
Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b . При Видео:Линейная функция и ее график. 7 класс.Скачать  Прямые, параллельные оси ординатПрямые, параллельные оси Oy , задаются формулой
где c – произвольное число, и изображены на рис. 13, 14, 15.
Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .; Видео:Уравнение прямой по графику. ПримерыСкачать  Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
где p, q, r – произвольные числа. В случае, когда что и требовалось. В случае, когда откуда вытекает, что уравнение (4) задает прямую линию вида (3). В случае, когда q = 0, p = 0, уравнение (4) имеет вид
и при r = 0 его решением являются точки всей плоскости: В случае, когда Замечание 2 . При любом значении r1 , не совпадающем с r прямая линия, заданная уравнением
параллельна прямой, заданной уравнением (4) . Замечание 3 . При любом значении r2 прямая линия, заданная уравнением
перпендикулярна прямой, заданной уравнением (4) . Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и
В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде
где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство Итак, уравнение прямой, параллельной к прямой В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде
где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать  График линейной функции, его свойства и формулыО чем эта статья: Статья находится на проверке у методистов Skysmart. Видео:Функция прямой пропорциональности. 7 класс.Скачать  Понятие функцииФункция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции. Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек. Видео:Линейная функция. Часть 4. Параллельность и перпендикулярность прямых.Скачать  Понятие линейной функцииЛинейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент. Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат. Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки. Если известно конкретное значение х, можно вычислить соответствующее значение у. Нам дана функция: у = 0,5х — 2. Значит:
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции. Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат. Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби. Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b». Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart! Видео:Прямая пропорциональность и её график. Алгебра, 7 классСкачать  Свойства линейной функции
Видео:Как запомнить графики функцийСкачать  Построение линейной функцииВ геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y. Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график: В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая. В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3). Теперь рассмотрим графики функций y = -2x + 3, y = — 1 /2x + 3, y = -x + 3. В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая. Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3). Рассмотрим графики функций y = 2x + 3, y = 2x, y = 2x — 2. Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые. При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты. Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b. Если k 0, то график функции y = kx + b выглядит так: 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»> Если k > 0 и b > 0, то график функции y = kx + b выглядит так: 0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»> Точки пересечения графика функции y = kx + b с осями координат:
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать  Решение задач на линейную функциюЧтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся! Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Видео:Параллельные прямые | Математика | TutorOnlineСкачать  4.13. Уравнения прямых на координатной плоскостиДавайте рассмотрим такие функций, графики которых имеют вид прямых. Простоты ради, мы будем иметь дело с безразмерными величинами, а значит, в качестве осей у нас будут выступать простые числовые прямые, и все наши чертежи мы будем делать на обычной координатной плоскости. Прямая, проходящая через начало координат Построение графика по заданной функции Пусть переменная (y) пропорциональна переменной (x) с коэффициентом пропорциональности (k) : Давайте договоримся, что (x) здесь — это независимая переменная, а (y) — зависимая. Коэффициент (k) играет роль константы (параметра). В таких случаях говорят, что (y) является (однородной) линейной функцией от (x) . Графиком этой функции, как мы хорошо знаем, является прямая, проходящая через начало координат ((0, 0)) . Для построения этой прямой нам достаточно определить еще какую-либо одну ее точку ((x_1, y_1)) . Для этого положим, например, (x_1 = 1) . Тогда (y_1 = k cdot 1 = k) . Проводим через эту точку и начало координат прямую линию. Это и есть график функции (y) от (x) . Так, по крайней мере, обстоит дело в теории, а на практике точку ((x_1, y_1)) лучше брать настолько далеко от начала координат, насколько позволяет чертеж. В этом стучае прямую удается провести наиболее точно. Ниже приведен пример такого построения для функции (y=frac x) . Восстановление функции по графику Решим теперь обратную задачу. Пусть на координатной плоскости с осями (x) и (y) нам дана прямая, проходящая через начало координат. Спрашивается: графиком какой функции она является? При этом подразумевается, что функция должна быть задана в виде формулы, связывающей переменные (x) и (y) . Такая формула носит название уравнения графика функции. В данном случае речь идет об уравнении прямой, проходящей через точку ((0,0)) . Заранее ясно, что это уравнение имеет вид От нас фактически только требуется найти значение константы (k) . Для этого отметим на прямой произвольную точку, отличную от ((0,0)) , и определим ее координаты ((x_1, y_1).) Эти координаты, очевидно, связаны соотношением При этом следует особо подчеркнуть, что константа (k) не зависит от выбора точки ((x_1, y_1).) Какую бы точку на прямой мы не выбрали в качестве ((x_1, y_1),) мы придем к одному и тому же значению (k) . Таким образом, Пример нахождения уравнения прямой приведен на следующем рисунке. Отметим два особых случая. Во-первых, прямая может совпасть с осью (x) . Тогда значение (y) остается постоянным и равным нулю на всем ее протяжении. Тем не менее наше общее решение остается в силе. При этом оказывается, что (k = 0) и переменную (y) можно всё еще формально считать функцией от (x) : Во-вторых, прямая может совпасть с осью (y) . В этом случае в каждой ее точке (x = 0) . Формула для константы (k) оказывается неприменимой, потому что число (x_0) , стоящее в знаменателе, обращается в нуль. Приходится признать, что мы не можем подобрать такую функцию (y) от (x) , которая имела бы подобный график. Разве что, мы можем теперь принять (y) за независимую переменную и формально рассматривать (x) как функцию от (y) Несложно убедиться, что всякая точка, лежащая на оси (y) , удовлетворяет этому равенству. Заметим, что если бы мы захотели написать уравнение прямой, проходящей через начало координат, в самом общем виде, то мы могли бы это сделать так: Это соотношение между (x) и (y) остается справедливым в обоих рассмотренных частных случаях, однако выбор параметров не является однозначным, так как в качестве пары чисел ((x_1, y_1)) можно взять координаты любой точки, принадлежащей прямой. Произвольная прямая Восстановление функции по графику Начнем с обратной задачи. Пусть теперь на координатной плоскости дана произвольная прямая, не проходящая через начало координат. Вопрос нас будет интересовать всё тот же: графиком какой функции она является или, короче говоря, каково уравнение этой прямой? Отметим на прямой две любые несовпадающие точки и обозначим их координаты через ((x_0, y_0)) и ((x_1,y_1)) . Поместим в точку ((x_0, y_0)) начало новой системы координат с осями (x’) и (y’) , сонаправленными с соответствующими осями (x) и (y) старой системы. Тогда координаты другой отмеченной точки в новой системе окажутся равны (begin x_1′ \ y_1′ end = begin x_1 \ y_1 end — begin x_0 \ y_0 end = begin x_1 — x_0 \ y_1 — y_0end.) Вообще, как мы знаем, новые («штрихованные») координаты любой точки связаны со старыми («нештрихованными») координатами соотношением Наша прямая проходит через начало координат новой системы, поэтому мы можем сразу же выписать ее уравнение в «штрихованных» переменных: Переходя к «нештрихованным» переменным, получаем Что и решает поставленную задачу. При желании, можно еще выразить функцию (y) от (x) в явном виде: (y = k,x — k,x_0 + y_0) (y = k,x + b,) где (b = — k,x_0 + y_0.) Значения констант (k) и (b) не зависят от выбора точек ((x_0, y_0)) и ((x_1,y_1)) . Какие бы точки на заданной прямой мы не взяли, мы всегда придем к одним и тем же значениям (k) и (b) . Заметим, что из-за дополнительного слагаемого (b) переменные (x) и (y) не пропорциональны друг другу. Поэтому константа (k) называется теперь не коэффициентом пропорциональности, как это было раньше, а угловым коэффициентом. Название это происходит от того, что значение (k) тесно связано с углом наклона прямой по отношению к оси (x) . Чем круче идет прямая, тем больше ее угловой коэффициент. Константу (b) иногда называют свободным членом. Как легко видеть, переменная (y) равна (b) при (x = 0) . Иными словами, (b) — это точка на оси (y) , в которой эта ось пересекается с нашей прямой. Если (b = 0) , то прямая проходит через начало координат, и мы возвращаемся к частному случаю, рассмотренному ранее. Из наших рассуждений следует, что любая прямая на координатной плоскости может быть описана уравнением вида при подходящем выборе констант (k) и (b) . Единственным исключением является особый случай, когда в выражении для углового коэффициента (k = frac) знаменатель обращается в ноль. Это происходит, если (x_1 = x_0) . Это значит, что прямая перпендикулярна оси (x) (и соответственно параллельна оси (y) ). При таких обстоятельствах (x) неизбежно утрачивает роль независимой переменной, но может формально рассматриваться как функция от (y) : (x = 0 cdot (y — y_0) + x_0.) В совершенно общем виде уравнение прямой можно написать следующим образом: ((x_1-x_0) (y-y_0) = (y_1-y_0) (x-x_0).) При этом, однако, выбор двух пар параметров ((x_0, y_0)) и ((x_1, y_1)) (которые, по смыслу, являются координатами двух произвольных точек, лежащих на прямой) неоднозначен. Построение графика по заданной функции Теперь давайте выясним, как построить график неоднородной линейной функции (y) от (x) , которая определяется как где (k) и (b) — любые действительные числа. Как мы только что выяснили, к такому виду сводится уравнение произвольной прямой (при условии, что она не параллельна оси (y) ). Строго говоря, это не исключает, что при некоторых значения параметров (k) и (b) график этой функции может отличаться от прямой линии. Давайте убедимся, что этого никогда не происходит. Перепишем данное нам уравнение следующим образом: Если перейти в новую, штрихованную, систему координат с началом в точке ((0, b)) и с осями (x’) и (y’) , сонаправленными с соответствующими осями старой системы, то в новых координатах уравнение примет вид: Мы получим тогда не что иное, как уравнение пропорциональной зависимости, которое гарантировано задает прямую линию. Значит, и график неоднородной линейной функции представляет собой прямую линию при любых значениях параметров (k) и (b) . Но для того, чтобы построить прямую, достаточно знать две ее произвольные точки ((x_0, y_0)) и ((x_1, y_1)) . В качестве (x_0) и (x_1) можно взять, например, соответственно ноль и единицу. Тогда (y_0 = b) (при (x_0 = 0) ), Проводим прямую через точки ((x_0, y_0)) и ((x_1, y_1)) — и задача решена. На практике, впрочем, лучше брать такие точки, которые расположены друг от друга по возможности дальше, насколько позволяет чертеж. Пример графика неоднородной линейной функции со значением параметров (k = frac) и (b = 1) представлен на следующем рисунке. Конспект (1) . Линейная функция (y = k,x + b) называется однородной при (b = 0) и неоднородной при (b ne 0.) Ее график на координатной плоскости представляет собой прямую линию, которая строится по двум произвольным точкам. (2) . Уравнение прямой, проходящей через начало координат: (y = frac x,) где ((x_1, y_1)) — координаты произвольной точки, принадлежащей этой прямой ((x_1 ne 0).) Исключение: прямая совпадает с осью (y) . Тогда уравнение прямой: (x = 0.) (3) . Уравнение произвольной прямой: (y-y_0 = frac (x-x_0),) где ((x_0, y_0)) и ((x_1, y_1)) — координаты двух различных произвольных точек, принадлежащих этой прямой. Исключение: прямая проходит через точку ((x_0, y_0)) параллельно оси (y) . Тогда уравнение прямой: (x = x_0) . 🎥 ВидеоЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать  Линейная функция и её график. Алгебра, 7 классСкачать  Урок ГРАФИК ЛИНЕЙНОЙ ФУНКЦИИ 7 КЛАСССкачать  Графики функций. Задание №11 | Математика ОГЭ 2023 | УмскулСкачать  Взаимное расположение прямых на плоскости. 7 класс.Скачать  ОГЭ по математике. Задача 5-2Скачать  Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать  Все графики функций за 20 секундСкачать  График функции. Как определить? #shortsСкачать  |

 , параллельны .
, параллельны . , пересекаются при любых значениях свободных членов.
, пересекаются при любых значениях свободных членов.



 прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле
прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле



 уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .
уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .

 получаем:
получаем:

 уравнение (5) решений вообще не имеет.
уравнение (5) решений вообще не имеет.














