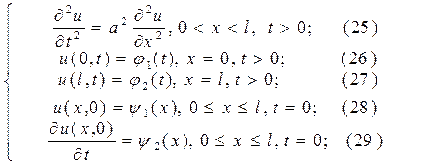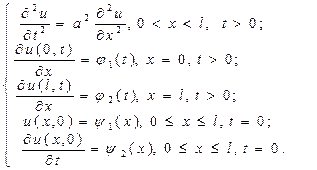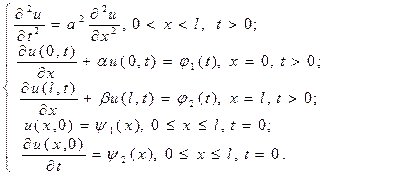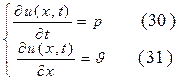Видео:2.1. Метод характеристик. Задача Коши для гиперболического уравнения на плоскости.Скачать
Метод характеристик при решение задачи коши для уравнений гиперболического типа
Стерлитамакский филиал Башкирский государственный университет
NovaInfo58, с. 11-15
Опубликовано 25 января 2017
Раздел: Физико-математические науки
Просмотров за месяц: 95
CC BY-NC
Видео:Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать
Аннотация
В статье рассматривается решение задачи Коши для уравнения гиперболического типа. Продемонстрировано решение данного уравнения методом характеристик.
Видео:6.1 Смешанные краевые задачи для уравнений гиперболического и параболического типов. Метод Фурье.Скачать
Ключевые слова
Видео:3.2 Решение уравнений гиперболического типа методом характеристикСкачать
Текст научной работы
Многие задачи физики, в частности механики, приводят к исследованию дифференциальных уравнений в частных производных второго порядка. Так, например, при изучении различных видов волн: звуковых, электромагнитных и других колебательных явлений приходят к волновому уравнению
где u=u(x,y,z,t), a — скорость распространения волны в данной среде. В одномерном случае это уравнение примет вид
которое является уравнением вынужденных колебаний однородной струны [1, 12].
В одномерном случае рассмотрим уравнение струны [2, 26]:
Задача Коши: Найти решение u(x,y) данного уравнения, удовлетворяющее начальным условиям:
Задача Коши для уравнения струны является математической моделью физической задачи о колебаниях настолько большой струны, что влияние ее концов уже не сказывается на колебаниях других точек струны. По этой причине в этой задаче отсутствуют граничные условия.
Приведем уравнение (1) к каноническому виду. Для этого составим уравнение характеристик
где A=0, 2B=e y , C=-1. Вычислим D=B^2-AC=frac<e^>>0
. Следовательно, уравнение (1) является уравнением гиперболического типа.
Подставляя в уравнение характеристик наши значения, получим:
Видео:Классические точные аналитические методы решения уравнений гиперболического и параболического типаСкачать
Постановка задачи для уравнения гиперболического типа
Классическим примером уравнения гиперболического типа является волновое уравнение, которое имеет вид:
, 0 0 (24)
В данном случае искомая функция u(x, t) описывает малые продольные или поперечные колебания стержня или туго натянутой струны, точкам которых в начальный момент времени t =0 сообщили начальное смещение y1(t)и скорость y2(t). В случае продольных колебаний параметр a характеризует скорость звука в материале, из которого изготовлен стержень, а для поперечных колебаний параметр a связан с массой единицы длины струны и силой её натяжения.
Первая начально-краевая задача. Если концы стержня движутся по заданным законам, то есть на концах заданы перемещения (значения искомой функции), то первая начально-краевая задача для волнового уравнения имеет вид:
При постановке первой начально-краевой задачи для волнового уравнения условием (28) задаётся начальное распределения значений искомой функции u(x, t) (характеризующей смещение точек стрежня или струны), а условием (29) задаётся ещё и начальная скорость такого смещения.
Вторая начально-краевая задача. Если на концах стержня заданы значения силы, которая по закону Гука пропорциональна производной перемещения по пространственной переменной (т.е. на концах заданы значения первых производных по пространственной переменной x), то ставится вторая начально-краевая задача для волнового уравнения:
В условиях, когда концы стержня свободны, то функции j 1(t) = j 2(t) = 0.
Третья начально-краевая задача. Если концы стержня или струны закреплены упруго, т.е. на концевые заделки действуют силы, пропорциональные перемещениям, то ставится третья начально-краевая задача для волнового уравнения
Аналогично ставятся двумерные трехмерные начально-краевые задачи для двумерного и трёхмерного волнового уравнения.
Замечание. Необходимо отметить, что волновое уравнение (24) легко трансформируется в систему уравнений акустики (13), являющихся простейшей линейной моделью газодинамических течений. Действительно, введём следующие обозначения:
Продифференцируем уравнение (30) по переменной t, а уравнение (31) по переменной x и подставим результат в волновое уравнение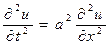 
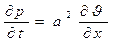
, при этом получим:
(32)
Далее продифференцируем уравнение (30) по переменной x, а уравнение (31) по переменной t ,в результате будем иметь:
и 
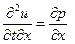
Полагая далее, что смешанные производные от u(x, t) по переменным x и t не зависят от порядка дифференцирования, получим:
(33)
Полученную систему уравнений (32), (33):
называют уравнениями акустики, как уже отмечалось выше, функции p и J характеризуют возмущения (т.е. слабые колебания) давления и скорости в акустической волне.
🌟 Видео
Задача Коши для волнового уравнения (Часть 1)Скачать
Уравнения математической физики. Лекция 5: Уравнения гиперболического типа (I). Лектор Хохлов Н.А.Скачать
УМФ. Метод Фурье для параболического уравненияСкачать
Принцип максимума для Параболического уравнения (Часть 1)Скачать
2.3. Задача Гурса для гиперболического уравнения на плоскости.Скачать
Уравнения математической физики. Решение гиперболического уравнения методом Фурье.Скачать
Решение первой краевой задачи для неоднородного уравнения теплопроводности.Скачать
Разбор решения задачи Штурма-ЛиувилляСкачать
Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать
Метод Фурье для неоднородного уравнения теплопроводностиСкачать
2.2. Локализованная задача Коши для гиперболического уравнения на плоскости.Скачать
Боголюбов А. Н. - Методы математической физики - Уравнения параболического типаСкачать
