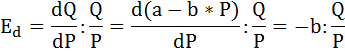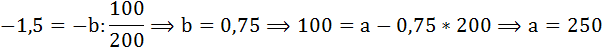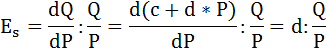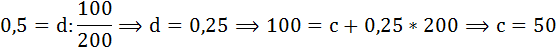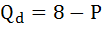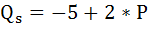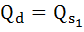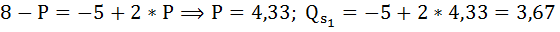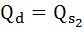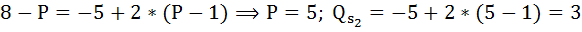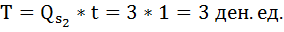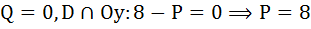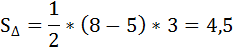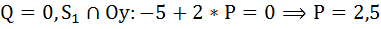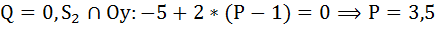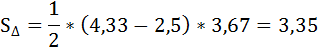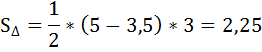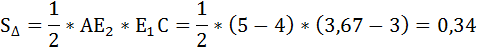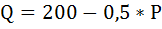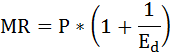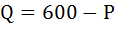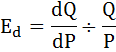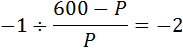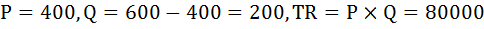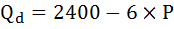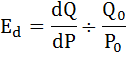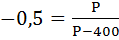Спрос и предложение на рынке на товар задаются линейными уравнениями. Известно, что равновесная цена равна 200 руб. за упаковку товара, а равновесное количество — 100 упаковок в день. В точке равновесия однопроцентное повышение цены на данный товар влечет снижение величины спроса на 1,5% и повышение величины предложения на 0,5%.
Определите уравнения кривых спроса и предложения, считая их линейными.
Решение:
Общая точка двух прямых спроса и предложения имеет координаты:
Общий вид линейной функции спроса:
Так как однопроцентное повышение цены на данный товар влечет снижение величины спроса на 1,5%, следовательно, коэффициент эластичности спроса равен:
Запишем формулу точечной эластичности спроса по цене:
Подставим имеющиеся по условию данные:
Тогда функция спроса на данный товар имеет вид:
Общий вид линейной функции предложения:
Так как однопроцентное повышение цены на данный товар влечет повышение величины предложения на 0,5%., следовательно, коэффициент эластичности предложения равен:
Формула эластичности предложения будет иметь вид:
Подставим имеющиеся по условию данные:
Тогда функция предложения на данный товар имеет вид:
Видео:Равновесная цена | Крест МаршаллаСкачать

Основы математики и ее приложения в экономическом образовании (стр. 11 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
Как и в предыдущем случае, в случае непрерывной зависимости Δ D от Δ Q удобно перейти к пределу при ΔР 
Аналогичное понятие можно ввести и для функции предложения S ( P ). Напомним, что функция D ( P ) убывает, а функция S ( P ) возрастает с ростом цены Р.
Укажем некоторые свойства эластичности. Как следует из формулы (5.14а), ее можно выразить так:
Из равенства (5.14 б) следует, что E ( D ) обладает свойствами логарифма, а значит,
Заметим, что поскольку функция D ( P ) убывающая, то D ‘( P ) E ( D ) Напротив, поскольку функция предложения возрастающая, то соответствующая эластичность E ( S ) > 0.
Различают три вида спроса в зависимости от величины | E ( D )| :
Рассмотрим два примера из этой области.
Пример 1. Пусть функция спроса описывается формулой
где D 0 и k — известные величины. Найти, при каких значениях цены Р спрос будет эластичным.
Р ешение . Согласно формуле (5.14а) составляем выражение для E ( D ):
Для того чтобы спрос был эластичным (случай а), необходимо, чтобы выполнялось неравенство
Пример 2. Найти изменение выручки с увеличением цены на товар при разных вариантах эластичности спроса.
Р ешение . Выручка I равна произведению цены Р на товар на величину спроса D:
Найдем производную этой функции:
Теперь проанализируем все варианты эластичности спроса, приведенные выше, с учетом формулы (5.14а).
1) E ( D ) -1; тогда, подставляя (5.14а) в это неравенство, получаем, что правая часть уравнения (5.15) отрицательна. Таким образом, при эластичном спросе повышение цены Р ведет к снижению выручки. Напротив, снижение цены на товар увеличивает выручку.
2) E ( D ) = — 1. Из (5.14а) следует, что правая часть (5.15) равна нулю, т. е. при нейтральном спросе изменение цены на товар не влияет на выручку.
3) E ( D ) > -1. Тогда I ‘( P ) > 0, т. е. при неэластичном спросе повышение цены Р на товар приводит к росту выручки.
Понятие эластичности распространяется и на другие области экономики. Рассмотрим один характерный пример.
Пример 3. Пусть зависимость между себестоимостью продукции С и объемом Q ее производства выражается формулой
Требуется определить эластичность себестоимости при выпуске продукции Q = 30 ден. ед.
Р ешение . По формуле (5.14а) получаем
откуда при Q = 30 искомая эластичность составит около —0,32, т. е. при данном объеме выпуска продукции его увеличение на 1% приведет к снижению себестоимости примерно на 0,32%.
Пусть Q — количество реализованного товара, R ( Q ) — функция дохода; C ( Q ) — функция затрат на производство товара. В реальности вид этих функций зависит в первую очередь от способа производства, организации инфраструктуры и т. п. Прибыль от реализации произведенного товара дается формулой
В микроэкономике известно утверждение: для того чтобы прибыль была максимальной, необходимо, чтобы предельный доход и предельные издержки были равны. Оба упомянутых предельных показателя определяются по аналогии с (5.14а), так что этот принцип можно записать в виде R ‘( Q ) = C ‘( Q ). Действительно, из необходимого условия экстремума для функции (5.16) следует, что П'( Q ) = 0, откуда и получается основной принцип.
Пример 4. Найти максимум прибыли, если доход и издержки определяются следующими формулами:
Р ешение . Согласно (5.16), прибыль П( Q ) = — Q 3 + 36 Q 2 — 69 Q — 4000. Приравнивая производную функции прибыли к нулю, получаем уравнение
Корни этого уравнения Q 1 = 1, Q 2 = 23. Проверка показывает, что максимальная прибыль достигается при Q = 23: П m ах = 1290.
Закон убывающей эффективности производства
Этот закон утверждает, что при увеличении одного из основных факторов производства, например капитальных затрат К, прирост производства начиная с некоторого значения К является убывающей функцией. Иными словами, объем произведенной продукции V как функция от К описывается графиком со сменой выпуклости вниз на выпуклость вверх.
Пример 5. Пусть эта функция дается уравнением
где b и с — известные положительные числа (они определяются прежде всего структурой организации производства), а Vlim — предельно возможный объем выпускаемой продукции. Нетрудно подсчитать, что вторая производная функции (5.17) имеет вид
Критическая точка находится из условия V «( K ) = 0, откуда
График функции (5.17) приведен на рис. 5.10. В точке перегиба (5.18) выпуклость графика функции вниз меняется на выпуклость вверх. До этой точки увеличение капитальных затрат приводит к интенсивному росту объема продукции: темп прироста объема продукции (аналог первой производной) возрастает, т. е. V «( K ) > 0. При К > Кcr темп прироста объема выпускаемой продукции снижается, т. е. V «( K )
Таким образом, в стратегии капиталовложений оказывается очень важным моментом определение критического объема затрат, сверх которого дополнительные затраты будут приводить все к меньшей отдаче при данной структуре организации производства. Зная этот прогноз, можно пытаться совершенствовать и менять структуру организации производства: «улучшать» показатели b, с и V lim в сторону повышения эффективности капиталовложений.
Найти пределы с использованием правила Лопиталя.
5.1. 

5.3. 

5.5. 


5.8. 

5.10. 

5.12. Разложить по формуле Маклорена функцию f ( x ) = tg x до члена с x 3 включительно.
5.13. Разложить по формуле Маклорена функцию f ( x ) = e-x до члена с x2 включительно.
Найти пределы с использованием разложений по формуле Маклорена.
5.14. 

5.16. 

Найти интервалы выпуклости и точки перегиба графиков функций.
5.18. 
5.20. 
Найти асимптоты графиков функций.
5.21. 

5.23. 
Исследовать и построить графики функций.
5.24. 

5.26. 

5.28. 

5.30. 
5.32. 

Решите задачи на наибольшее и наименьшее значения.
5.34. Разложить число 12 на два слагаемых так, чтобы их произведение было наибольшим.
5.35. Определить размеры открытого бассейна с квадратным дном объемом V, при которых на облицовку дна и стен пойдет наименьшее количество материала.
5.36. Даны точки А(0, 3) и В(4, 5). На оси Ох найти точку, сумма расстояний от которой до точек А и В наименьшая.
Решите задачи с экономическим содержанием.
5.37. Зависимость между издержками производства С и объемом продукции Q выражается функцией С = 30 Q — 0,08 Q 3 . Определить средние и предельные издержки при объеме продукции: а) Q = 5 ед., б) Q = 10 ед.
5.38. Функции долговременного спроса D и предложения S от цены р на мировом рынке нефти имеют соответственно вид
1) Найти эластичность спроса в точке равновесной цены.
2) Как изменятся равновесная цена и эластичность спроса при уменьшении предложения нефти на рынке на 25%?
5.39. Функции спроса D и предложения S от цены р выражаются соответственно уравнениями
Найти эластичность спроса и предложения при равновесной цене, а также изменение дохода (в процентах) при увеличении цены на 10%.
5.40. Зависимость объема выпуска продукции V от капитальных затрат К определяется функцией V = V 0 ln (4 + K 3 ). Найти интервал изменения К, на котором увеличение капитальных затрат неэффективно.
6.1. Первообразная и неопределенный интеграл
Понятие первообразной функции
Предыдущие главы были посвящены одной из основных задач дифференциального исчисления — нахождению производной заданной функции. Множество вопросов математического анализа и приложений в разнообразных науках приводит к другой задаче: по данной функции f ( x ) найти такую функцию F ( x ), производная которой равна функции f ( x ).
Определение 1. Функция F ( x ) называется первообразной для функции f ( x ) на промежутке X, если для любого х 
Пример 1. Функция F ( x ) = sin x является первообразной для функции f ( x ) = cos x на бесконечном промежутке (-

Пример 2. Функция F ( x ) = ln x — первообразная для функции f ( x ) = 1/ x на промежутке (0, +
Видео:Спрос и предложение разбор задачСкачать

Решение задач по спросу и предложение
Условие задачи
Спрос и предложение фирмы на рынке описываются уравнениями: Qd=200-5Р; Qs=50+Р. Определите параметры рыночного равновесия.
Решение
Рыночное равновесие достигается при равенстве объемов спроса Qd и предложения Qs :
Подставив в равенство функции спроса и предложения, получим:
200 — 5Р = 50 + Р
200 – 50 = Р + 5Р
Р = 25
Для того чтобы определить равновесный объем, необходимо в уравнение спроса или предложения подставить равновесную цену:
200 – 5 × 25 = 75 ед.
Таким образом, равновесная цена составляет 25 ден. ед., а равновесный объем – 75 ед.
Задача 2. Расчет параметров рыночного равновесия при введении налога на потребителей ↑
Условие задачи
Кривая спроса описывается уравнением Qd=70-2Р, а кривая предложения — уравнением Qs=10+Р. Правительство ввело налог на потребителей в размере 9 долл. за единицу. Определите:
- как изменятся равновесные цена и объем продукции;
- каков доход государства от введения этого налога;
- в какой степени пострадают от введения этого налога потребители и производители.
Решение
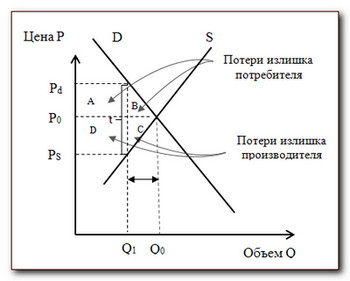
До введения налога рыночное равновесие достигалось при цене Р0 и объеме Q0(на рисунке — в точке пересечения кривых спроса D и предложения S). Рассчитаем параметры равновесия:
70 — 2Р=10 + Р
3Р=60
Р=20 долл.
Q0=30 ед.
В результате введения налога произойдут следующие изменения:
Последствия введения налога
- Поскольку вводится налог на потребителей, то для них цена возрастет и составит Pd. Количество товара, которое потребители приобретут по данной цене, составит Q1(на рисунке — точка пересечения кривой спроса D и цены Pd).
- Чистая цена, которую получат производители, составит Ps. Количество товара, которое производится при данной цене Ps, составит Q1 (на рисунке — точка пересечения кривой предложения S и цены Ps).
Теперь по пунктам ответим на поставленные в задаче вопросы.
1. Как изменятся равновесные цена и объем продукции? Рыночное равновесие достигается тогда, когда объем продаж производителя равен объему покупок потребителя:
Равновесный объем продаж Q1 после введения налога соответствует цене Pd на кривой спроса и цене Ps на кривой предложения. Разница между ценой покупки Pd и ценой продажи Ps составляет величину налога t:
Так как кривые спроса, предложения и размер налога заданы, параметры рыночного равновесия после введения налога можно найти из уравнений:
Подставив первые два уравнения в третье получим:
Введение налога на потребителей приведет к росту цены продажи. Она составит Pd= Ps + 9. Подставляем Pd в уравнение и получим:
Подставив равновесную цену Ps в уравнение предложения, получим равновесный объем Q1:
Тот же результат можно получить, если подставить цену покупки Pd в уравнение спроса:
Q1 = 70 – 2 × 23 = 24
После введения налога на потребителей в размере 9 долл. за ед. равновесный объем на рынке составит 24 ед. при равновесной цене (Ps ) 14 долл. за ед. Таким образом,введение налога на потребителей приведет к сокращению равновесного объема на 6 ед. (30 – 24) и равновесной цены на 6 долл. (20 – 14).
2. Каков доход государства от введения налога? За каждую единицу проданного товара государство получит 9 долл. Общая сумма налогов, полученных государством, составит:
Дг = Q1 × t = 24 × 9 = 216 долл.
Графически общая сумма доходов государства представлена на рисунке суммарной площадью прямоугольников A и D.
3. В какой степени пострадают от введения этого налога потребители и производители? Для того чтобы определить, каким образом налоговое бремя распределяется между покупателями и производителями, необходимо определить размер их потерь в результате введения налога. Объем покупок потребителей в результате введения налога сократился с 30 ед. до 24 ед., а цена покупки возросла с 20 долл. до 23 долл. Общие потери потребителей (в результате роста цены и сокращения объема покупок) с введением налога графически представлены суммарной площадью фигур А и В. При налоге потребителям каждая единица товара обходится на 3 долл. дороже, чем без налога, т.е. они дополнительно тратят:
Q1 × 3 = 24 × 3 = 72 долл.
Таким образом, оплачиваемая потребителями часть налоговых поступлений составит 72 долл. (на рисунке – площадь прямоугольника А) В результате введения налога цена продажи сократилась с 20 долл. до 14 долл. за ед. , а значит за каждую единицу товара производитель получит на 6 долл. меньше. Его потери в результате сокращения цены составят:
Q1 × 6 = 24 × 6 = 144 долл.
Часть налоговых поступлений , оплачиваемая производителями, графически представлена на рисунке площадью прямоугольника D. Результаты расчета свидетельствуют о том, что при введении налога на потребителей производители оплачивают в 2 раза большую часть налоговых поступлений, чем сами потребители.
Задача 3. Расчет параметров рыночного равновесия при введении налога на производителей ↑
Условие задачи
Предположим, что кривая спроса описывается уравнением Qd =400- Р, а кривая предложения — уравнением Qs= 100 + 2Р. Правительство ввело налог на производителей в размере 15 долл. за единицу продукции.
- как изменятся равновесные цена и объем продукции;
- каков доход государства от введения этого налога;
- в какой степени пострадают от введения этого налога потребители.
Решение
1. Задача решается аналогично предыдущей (см. Задача 2), с той лишь разницей, что налогом облагаются не потребители, а производители. Определяем параметры рыночного равновесия до введения налога:
400 — Pd = 100 + 2(Pd – 15)
3Pd = 330
Pd = 110 ден. ед.
Ps = 110-15 = 95 ден. ед.
Q1 = 400 – 110 = 290 ед.
Параметры рыночного равновесия после введения налога определяем с помощью уравнений:
Введение налога на производителей приведет к тому, что получаемая ими чистая цена уменьшится. Введение налога на производителей не отразится на цене покупки Pd, а цена продажи будет равна Ps = Pd – 15. Сделав все необходимые подстановки, получаем:
400 — Pd = 100 + 2(Pd – 15)
3 Pd = 330
Pd = 110 долл.
Ps = 110 – 15 = 95 долл.
Q1 = 400 – 110 = 290 ед.
После введения налога на производителей равновесный объем составил 290 ед., а равновесная цена – 110 долл. Таким образом, равновесный объем сократился на 10 ед., а равновесная цена возросла на 10 долл.
2. За каждую единицу проданного товара государство получит 15 долл. Общая сумма налогов, полученных государством, составит:
Дг = Q1 × t = 290 × 15 = 4350 долл.
3. При налоге на производителей каждая единица товара обходится потребителям на 10 долл. дороже (до налога цена покупки составляла 100 долл., при налоге -110 долл.). Часть налоговых поступлений, оплачиваемая потребителями, составит:
Q1 × 10 = 290 × 10 = 2900 долл.
До введения налога цена продажи составляла 100 долл., а после введения налога – 95 долл., т.е. при налоге производители за каждую проданную единицу товара получают на 5 долл. меньше. Часть налоговых поступлений, оплачиваемая производителями, составит:
Q1 × 5 = 290 × 5 = 1450 долл.
Таким образом, при введении налога на производителей покупатели оплачивают в 2 раза большую часть налоговых поступлений, чем производители.
Задача № 4
По данным таблицы 1. характеризующим различные ситуации на рынке консервированного зелёного горошка необходимо:
а) Начертить кривую спроса и предложения
б) Если рыночная цена на банку горошка составляет 1 гр. 60 коп., что характерно для данного рынка — излишек или дефицит? Каков их объём?
в) Если рыночная цена на банку горошка составляет 3 гр. 20 коп. , что характерно для данного рынка — излишек или дефицит? Каков их объём?
г) Чему равна равновесная цена на этом рынке?
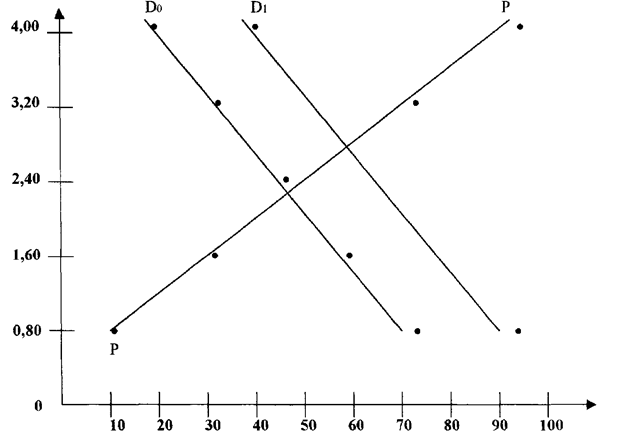
д) Рост потребительских расходов повысил потребление консервированного горошка на 30 млн. банок при каждом уровне цен. Какова будет равновесная цена и равновесный объём производства?
| № | Цена (грн.) | Объём спроса (млн. банок) | Объём предложения (млн. банок) |
| 0,80 | |||
| 1,60 | |||
| 2,40 | |||
| 3,20 | |||
| 4,00 |
Задача 5.
По данным таблицы 2. характеризующей различные ситуации на рынке электродрелей необходимо:
а) Начертить кривые спроса и предложения
б) Какова равновесная цена на рынке электродрелей?
в) Каков равновесный объём купли-продажи электродрелей?
г) Если цена электродрели составит 30 грн. , какова величина дефицита на этом рынке?
д) Если цена электродрели повысится до 60 грн., какова величина избытка на этом рынке?
Объём (тыс./штук)
| Цена (грн.) |
| Спроса |
| Предложения |
Задача 6.
Функция спроса выражается уравнением у = 5 — 1 / 2р
а) Определить количество товара, которое могут приобрести покупатели по ценам р = 1; р = 2; р = 3;
б) Установите значение объёма насыщения и запретительной цены;
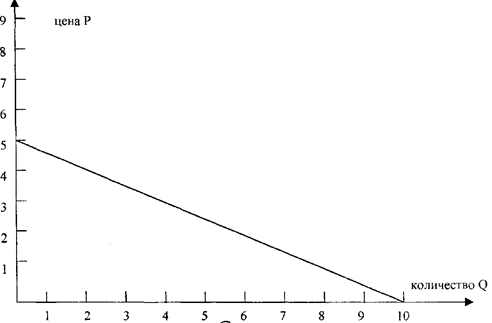
в) Изобразите графически функцию спроса в системе координат Р : Q.
Задача 7.
Для товара Q на рынке заданы следующие значения функции:
Функция предложения: p = l+3/2Q
Функция спроса: p = 5-l/2Q
а) Какое количество товара предложит продавец по цене р = 3;р = 6;р = 9
б) Какое количество товара предложит продавец по цене р = 1
в) Представьте обе функции графически и определите равновесную цену и равновесное количество
2) Почему цены р = 4,5 и р = 3 не являются равновесными
Решение задач по спросу и предложение.
Задача 4. – решение:
А) (Смотрите рис. 3)
б) дефицит, равный 30 млн. банок в год г) Равновесная цена равна 2 грн. 40 коп.
в) излишек 130 млн. банок в год д) Равновесная цена составит 3 грн. 20 коп.
равновесный объём 60 млн. банок
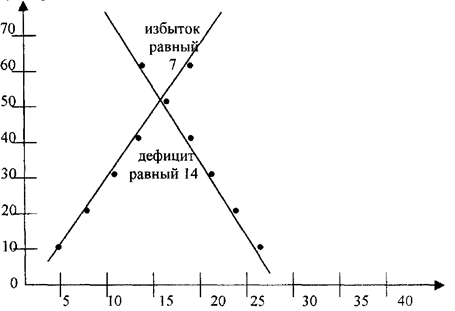
Задание 5
б) 50 г) Дефицит, равный 14 тыс. штук
в) 16 д) Избыток, равный 7 тыс. штук
Задание 6.
а) Если подставить значения цен в функцию спроса, то значения количества товаров будут следующими: Q = 8 при Р =1; Q = 6 при Р = 2; Q = 4 при Р = 3;
б) Объём насыщения Q, будет осуществлён при Р = 0; Q = 10. Запретительная цена — это цена, при которой пользующиеся спросом количество равно нулю;
Задание 7.
а) Если данные цены подставить в функцию предложения, то получим следующие количества предлагаемого в каждом отдельном случае товара:
Q = 11/3 при Р = 3
Q = 31/3 при Р = 6
Q = 51/3 при Р = 9
б) при Р = 1 продавцы вообще ничего не предлагают. Причина в том, что их расходы были выше чем цена
Х = 2 спрос
Точка пересечения будет находиться на пересечении обоих кривых. Если сопоставить функцию предложения и спроса, получим: l+3/2Q = 5-l/2Q Q = 2;P = 4.
г) Ни одна из этих цен не может обозначать равновесную цену, потому, что предложенное и пользующееся спросом количество товара в данном случае разное. При цене Р = 4,5 предложенное количество товара составит Q = 7 / 3, а пользующееся спросом — Q = 1 т. е. возникает превышение предложения. Противоположной является ситуация при Р — 3. Предложенное количество составит Q = 1 / 3, а пользующееся спросом Q — 4 т. е. наблюдается превышение спроса. Обе величины не могут существовать на протяжении длительного времени, если цены устанавливаются свободно.
Задача №8. Расчёт цены покупателя и цены продавца, суммы налога, излишков, чистых потерь
Спрос и предложение
Функция спроса населения на данный товар имеет вид:
Предположим, на данный товар введён налог, уплачиваемый продавцом, в размере 1 ден. ед.
а) цену для покупателя и цену для продавца с учётом налога;
б) общую сумму вносимого в бюджет налога;
в) излишек покупателя и излишек продавца до и после введения налога;
г) чистые потери общества.
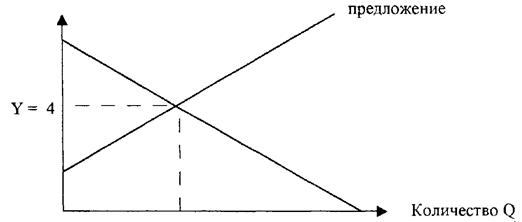
а) Найдём равновесную цену и объём до введения налога.
После введения налога кривая предложения сдвинется вверх на величину налога. Найдём равновесную цену и объём после введения налога:
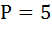
Для того, чтобы определить цену продавца, в первоначальную функцию предложения подставим равновесный объём после введения налога.
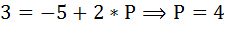
Точка А будет иметь координаты (3,4).
б) Определим общую сумму вносимого в бюджет налога. Она численно будет равна площади прямоугольника (5, E2, А, 4):
в) Для нахождения излишка покупателя и излишка продавца до и после введения налога воспользуемся графиком:
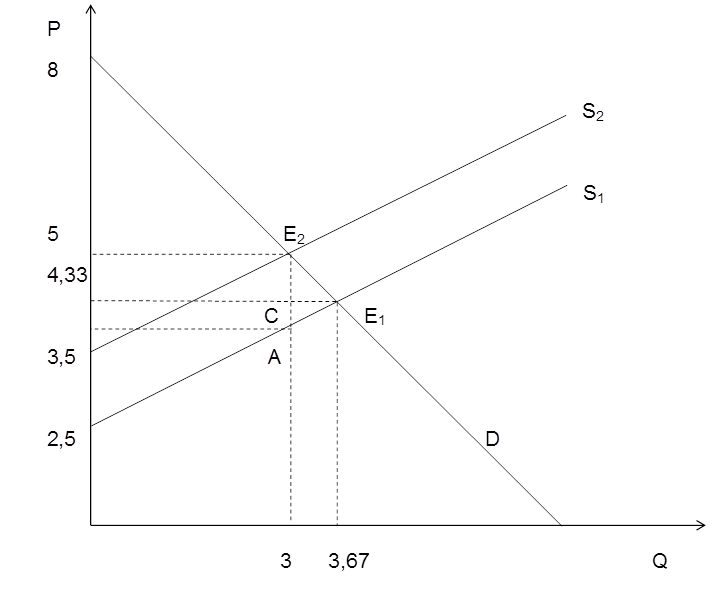
Найдём точку пересечения графика функции спроса с осью оу:
При
Излишек покупателя до введения налога численно равен площади треугольника (4,33; E1; 8):
Излишек покупателя после введения налога численно равен площади треугольника (8; 5; E2):
Найдём точки пересечения графиков функций предложения с осью оу:
При
При
Излишек продавца до введения налога численно равен площади треугольника (4,33; E1; 2,5):
Излишек продавца после введения налога численно равен площади треугольника (5; E2; 3,5):
г) Чистые потери общества численно равны площади треугольника (А, Е1, Е2):
Задача №9. Определение изменения дохода при увеличении проданной продукции на одну единицу
Фирма имеет кривую спроса:
Зная, что P=100, определить изменение дохода при увеличении проданной продукции на одну единицу.
Прирост дохода при увеличении проданной продукции на одну единицу называют предельной выручкой (MR — marginal revenue).
Предельная выручка может быть представлена как частная производная общей выручки по количеству товара.
Кроме того цена и объём связаны между собой функциональной зависимостью: Р = f(Q).
Легко заметить, что второе слагаемое в скобках есть обратное значение эластичности спроса:
Определим эластичность спроса по цене:
Таким образом, увеличение количества проданной продукции на единицу, уменьшит доход фирмы на 200 единиц.
Задача №10. Расчёт выручки
Кривая спроса на продукцию монополиста описывается уравнением
Монополист установил такую цену на товар, при которой эластичность спроса на него равна (-2). Определить величину выручки монополиста.
Запишем уравнение кривой спроса в привычном виде: выразим величину спроса Qчерез цену P.
Эластичность спроса в случае непрерывной функции рассчитывается по формуле:
И равна по условию
Задача №11. Эластичность спроса по цене
Функция задана уравнением
а) Выведите формулу эластичности этого спроса.
б) При какой цене эластичность спроса по цене составит – 0,5?
в) При какой цене в интервале цен от 200 до 300 эластичность будет максимальной по абсолютной величине?
а) Так как в условии задачи нам дана непрерывная функция, для вывода формулы эластичности этого спроса воспользуемся коэффициентом точечной эластичности.
В точке (P0,Q0) точечная эластичность вычисляется как
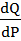
б)
в) Чем больше P, тем больше эластичность по абсолютной величине. Поэтому на интервале цен от 200 до 300 она достигает максимума в точке Р=300.
Задача 1
Постановка задачи:Зависимость объема спроса товара Х от его цены представлена в таблице.
| Цена (Р) (долл.) | Объем спроса (Qd) (кг) |
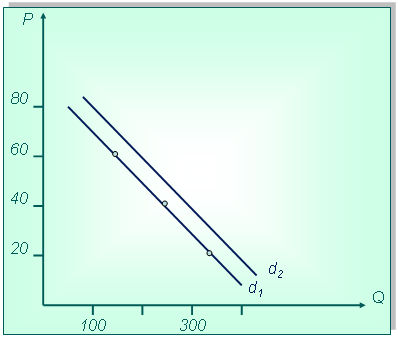
Нарисуйте кривую спроса данного товара и покажите, как она изменится, если покупатели будут предпочитать приобретать на 20 кг больше при каждом уровне цен?
Технология решения задачи:Сначала нарисуем систему координат и выберем масштаб, затем поставим точки, соответствующие значениям объема спроса при определенной цене. Соединив точки, получим кривую спроса. Увеличение спроса на 20 единиц изменит предпочтения потребителей, что проявится в увеличении объема спроса. Так, при цене 20 $ покупатели будет готовы приобрести не 320 кг, а 340, при цене 30 $ — 300 кг, при 40 $ — 260. Построим еще один столбец в таблице:
| Цена (Р) (долл.) | Объем спроса (Qd1) (кг) | Объем спроса (Qd2) (кг) |
В результате сдвинется и кривая спроса, она разместится правее d1.
Задача 2
Постановка задачи:Зависимость объема спроса товара Х от его цены представлена в таблице.
| Цена (Р) (тыс. руб.) | Объем спроса (Qd) (шт.) |
Нарисуйте кривую спроса данного товара.
Технология решения задачи:Сначала нарисуем систему координат и выберем масштаб, затем поставим точки, соответствующие значениям объема спроса при определенной цене. Соединив точки, получим кривую спроса.
Задача 3
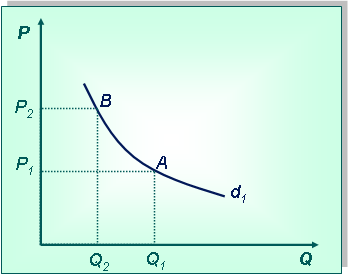
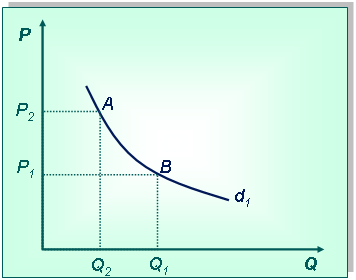
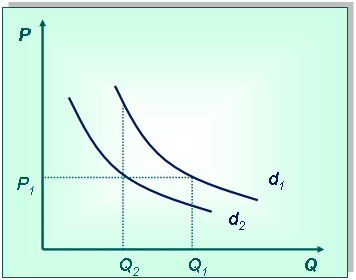
Постановка задачи:Дана кривая спроса d1 на услуги химчистки. Покажите, как изменится спрос, если химчистка объявит об увеличении тарифа на свои услуги.
Технология решения задачи:Сначала нарисуем систему координат и изобразим кривую спроса (при этом кривая не должна быть очень пологой, т. к. заменителей у данного производства мало).
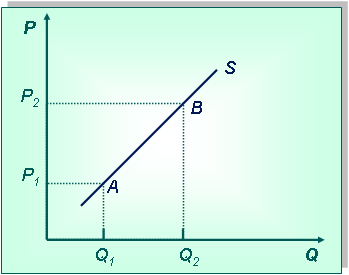
Повышение тарифов приводит к уменьшению спроса на услуги, что изображается перемещением точки А в В по кривой спроса, поскольку меняется ценовой фактор. Объем спроса при этом уменьшится с Q1 до Q2.
Задача 4
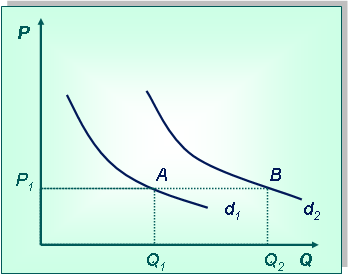
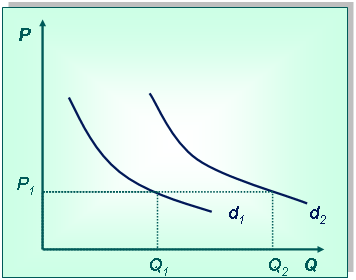
Постановка задачи:Дана кривая спроса d1 на товар Х. Покажите изменение спроса, если товар станет более модным.
Технология решения задачи:Сначала нарисуем систему координат и изобразим кривую спроса (при этом вид кривой не имеет значения). Возьмем любую цену и отметим на кривой спроса точку А, которая характерна для этой цены, при этом объем спроса будет Q1.
Если товар Х станет модным, то кривая спроса сдвинется вправо в положение d2, что приведет к увеличению спроса на товар. Это можно изобразить перемещением точки А в точку B на новой кривой спроса при той же цене Р1. Объем спроса при этом увеличится с Q1 до Q2.
Задача 5
Постановка задачи:Первоначально кривая спроса на товар Х находилась в положении d1. Покажите изменение спроса, если на товар У увеличится цена (товар Х и У – заменители).
Технология решения задачи:Сначала нарисуем систему координат и изобразим кривую спроса на товар Х (при этом вид кривой не имеет значения). Возьмем любую цену и отметим на кривой спроса точку А, которая характерна для этой цены, при этом объем спроса будет Q1.
Если цена товара У увеличится, то спрос на него упадет и часть потребителей перейдет на потребление товаров-заменителей, в том числе товара Х. При этом кривая спроса на товар Х сдвинется вправо в положение d2, что приводит к увеличению спроса на товар. Это можно изобразить перемещением точки А в точку Bна новой кривой спроса при той же цене Р1. Объем спроса при этом увеличится с Q1 до Q2.
Задача 6
Постановка задачи:Изобразите произвольную кривую спроса на товар А. Покажите изменение спроса, если на рынок пришли новые покупатели.
Технология решения задачи:Сначала нарисуем систему координат и изобразим кривую спроса (при этом вид кривой не имеет значения). Возьмем любую цену и отметим на кривой спроса точку A, которая характерна для этой цены, при этом объем спроса будет Q1.
Если на рынок товара А пришли новые покупатели, то кривая спроса сдвинется вправо в положение d2, что приводит к увеличению спроса на товар. Это можно изобразить перемещением точки A в точку B на новой кривой спроса при той же цене Р1. Объем спроса при этом увеличится с Q1 до Q2.
Задача 7
Постановка задачи:Цены на видеомагнитофоны снизились. Покажите на графиках, что произойдет на рынке видеомагнитофонов и рынке видеокассет.
Технология решения задачи:Сначала нарисуем систему координат и изобразим кривую спроса на видеомагнитофоны.
Понижение цен приведет к увеличению спроса на видеомагнитофоны, что изображается перемещением точки А в В по кривой спроса, поскольку меняется ценовой фактор. Объем спроса при этом увеличивается с Q1 до Q2.
Так как видеомагнитофоны и видеокассеты – товары комплиментарные (взаимодополняющие друг друга), то на рынке видеокассет тоже произойдут изменения. Поскольку спрос на видеомагнитофоны вырос, то и на видеокассеты он тоже увеличится.
Рассмотрим это на графике:
Кривая спроса на видеокассеты сдвигается вправо, поскольку изменяется неценовой фактор, и при той же цене Р1 объем спроса увеличится с Q1 до Q2.
Задача 8
Постановка задачи:Дана кривая спроса d1 на товар А. Покажите, как изменится положение этой кривой, если сезон на потребление товара закончится.
Технология решения задачи:Сначала нарисуем систему координат и изобразим кривую спроса d1. Если сезон потребления товара закончился, то спрос на него упадет и кривая спроса сдвинется влево (вниз), при этом объем спроса при той же цене Р1 уменьшится с Q1 до Q2.
Задача 9
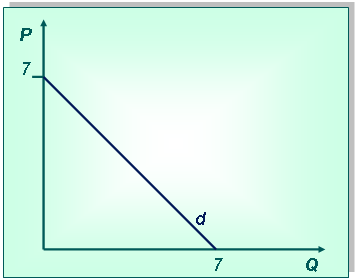
Постановка задачи:Функция спроса задана формулой Qd = 7-Р. Постройте кривую спроса.
Технология решения задачи:
1-й способ. Нарисуем систему координат и выберем масштаб, затем поставим точки, соответствующие значениям объема спроса при определенной цене. (Например, Р=1, Qd=6; Р=2, Qd=5 и т. д.) Соединив точки, получим кривую спроса.
2-й способ.Сначала нарисуем систему координат и выберем масштаб. Затем определим точки, соответствующие значениям объема спроса при нулевой цене и цене при объеме, равном нулю. Соединив точки, получим кривую спроса.
Задача 10
Постановка задачи:Зависимость объема предложения товара А от его цены представлена в таблице:
| Цена (Р) (тыс. руб.) | Объем предложения (Qs) (шт.) |
Нарисуйте кривую предложения данного товара.
Технология решения задачи:Сначала нарисуем систему координат и выберем масштаб, затем поставим точки, соответствующие значениям объема предложения при определенной цене. Соединив точки, получим кривую предложения.
Задача 11
Постановка задачи:Зависимость объема предложения товара А от его цены представлена в таблице:
| Цена (Р) (тыс. руб.) | Объем предложения (Qs) (шт.) |
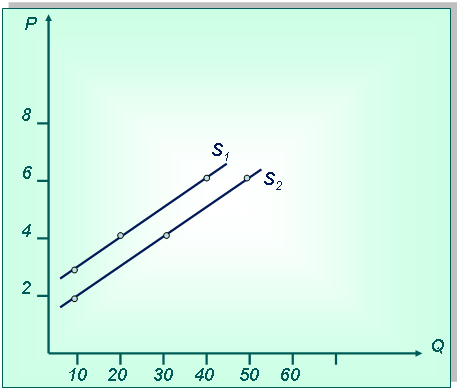
Покажите на графике, что произойдет с кривой предложения данного товара, если производители увеличат предложение товара А на 10 единиц при каждом уровне цен.
Технология решения задачи:Сначала нарисуем новую таблицу, чтобы показать изменения в предложении товара.
| Цена (Р) (тыс. руб.) | Объем предложения (Qs1) (шт.) | Объем предложения (Qs2) (шт.) |
Теперь нарисуем систему координат и выберем масштаб, затем поставим точки, соответствующие значениям объема предложения при определенной цене. Соединив точки, получим кривую предложения s1. Затем построим новую кривую предложения s2, соответствующую новым значениям предложения при разных ценах.
Задача 12
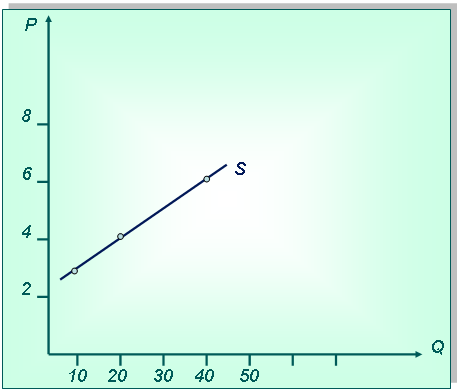
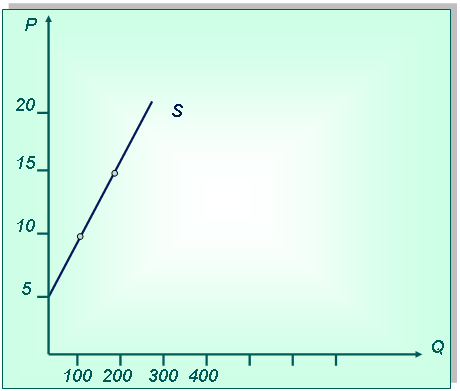
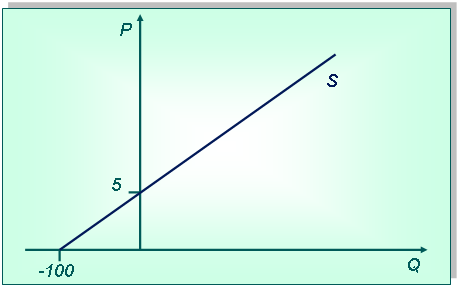
Постановка задачи:Функция предложения товара У задана формулой Qs = –100 + 20Р. Нарисуйте кривую предложения.
Технология решения задачи:
1-й способ. Нарисуем систему координат и выберем масштаб, затем поставим точки, соответствующие значениям объема предложения при определенной цене (например, Р=5, Qs=0; Р=10, Qs=100 и т. д.). Соединив точки, получим кривую предложения.
2-й способ.Сначала нарисуем систему координат и выберем масштаб. Затем определим точки, соответствующие значениям объема предложения при нулевой цене (Qs = –100 + 20*0= –100) и цене при объеме предложения, равном нулю (0= –100 + 20*Р, Р=5). Соединив точки, получим кривую предложения.
Задача 13
Постановка задачи:Дана кривая предложения на товар Х. Покажите изменение предложения, если в производстве будет применяться более дорогое сырье.
Технология решения задачи:Сначала нарисуем систему координат и изобразим кривую предложения (при этом вид кривой не имеет значения). Возьмем любую цену и отметим на кривой предложения точку А, которая характерна для этой цены, при этом объем предложения будет Q1. Применение более дорогого сырья приведет к росту издержек производства, объем производства сократится, а следовательно уменьшится, и объем предложения товара на рынке. Кривая предложения сдвинется влево (вверх), и при той же цене объем предложения уменьшится до Q2.
Задача 14
Постановка задачи:Цена товара А выросла. Покажите на графике, что произойдет с предложением этого товара.
Технология решения задачи:Сначала нарисуем систему координат и изобразим кривую предложения (при этом вид кривой не имеет значения). Возьмем любую цену Р1 и отметим на кривой предложения точку А, которая характерна для этой цены, при этом объем предложения будет Q1. Повышение цены приведет к росту дохода, поэтому производитель будет увеличивать производство этого товара, следовательно, и объем предложения товара на рынке увеличится. Кривая предложения при этом не изменяется, т. к. происходит изменение ценового фактора, что отразится на самой кривой. Точка переместится в положение B, объем предложения увеличится до Q2.
Задача 15
Постановка задачи:Государство ввело налог на товар А. Покажите на графике, какие изменения произойдут в предложении товара.
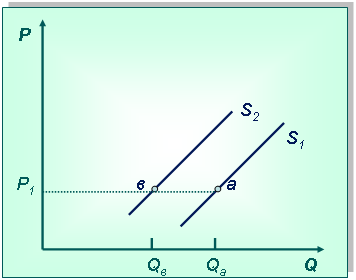
Технология решения задачи:Сначала нарисуем систему координат и изобразим кривую предложения (при этом вид кривой не имеет значения). Возьмем любую цену Р1 и отметим на кривой предложения s1 точку а, которая характерна для этой цены, при этом объем предложения будет Qa. Введение налога приведет к снижению дохода, поэтому производитель будет уменьшать производство этого товара, следовательно, и объем предложения товара на рынке уменьшится. Кривая предложения при этом сдвинется влево в положение s2, т. к. происходит изменение неценового фактора. Точка переместится в положение в, объем предложения уменьшится до Qв.
Задача 16
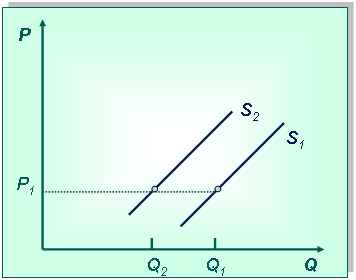
Постановка задачи:Государство ввело дотацию на производство товара Х. Как изменится положение кривой предложения этого товара?
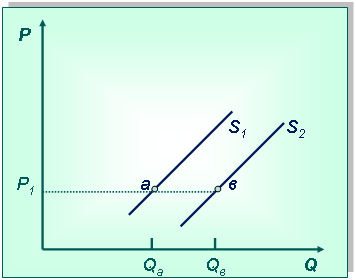
Технология решения задачи:Сначала нарисуем систему координат и изобразим кривую предложения s1 (при этом вид кривой не имеет значения). Возьмем любую цену и отметим на кривой предложения точку а, которая характерна для этой цены, при этом объем предложения будет Qa. Получение дотации снизит издержки предприятия, а доход вырастет, поэтому производство продукции увеличится, возрастет и объем предложения товара на рынке. Кривая предложения при этом сдвинется вправо в положение s2. Точка переместится в положение в, объем предложения увеличится до Qв.
Задача 17
Постановка задачи:Изобразите произвольную кривую предложения на товар А. Покажите изменение предложения, если на рынок пришли новые продавцы.
Технология решения задачи:Сначала нарисуем систему координат и изобразим кривую предложения (при этом вид кривой не имеет значения). Возьмем любую цену и отметим на кривой предложения точку а, которая характерна для этой цены, при этом объем предложения будет Qa. Появление на рынке новых продавцов приведет к увеличению объема предложения товара на рынке. Кривая предложения при этом сдвинется вправо в положение s2, т. к. происходит изменение неценового фактора. Точка переместится в положение в, объем предложения увеличится до Qв.
🎥 Видео
Как спрос и предложение задают ценыСкачать

Что такое спрос и предложение? Неценовые факторы спроса и предложения | обществознание ЕГЭ 2022Скачать

Эластичность спроса и предложения | Как цена влияет на спросСкачать

Линейные функции спроса и предложения, определение равновесной ценыСкачать
Графики спрос и предложение, равновесная цена. Для ЕГЭСкачать

Разбор листка «Линейные уравнения. Сложение спроса и предложения» (Ми-1)Скачать

Пси 22/23 - Спрос и предложение - Неделя 1 - ПрактикаСкачать

2.3.5. Обратные функции спроса и предложенияСкачать

2.3 Рыночное равновесиеСкачать

2.1 Спрос и величина спросаСкачать
Микра для начинающих/Эластичность_3Скачать

Тема 2. Задача 1Скачать

Экономика доступным языком: Спрос и предложение. Рыночное равновесие.Скачать

Спрос и предложение. Олмат.Экономика.Скачать

Микра для начинающих/Предложение_1Скачать

2.6 Спрос, предложение и общественное благосостояниеСкачать

3.1 Ограничения модели спроса и предложенияСкачать

Теория спроса и предложенияСкачать