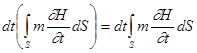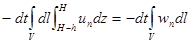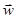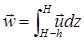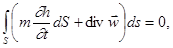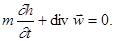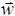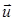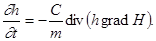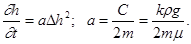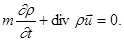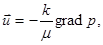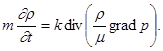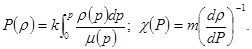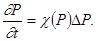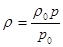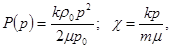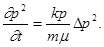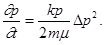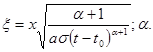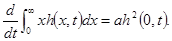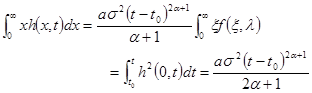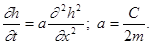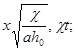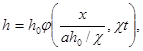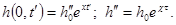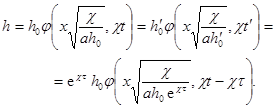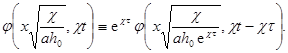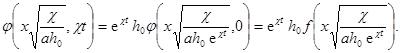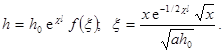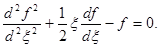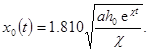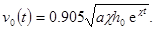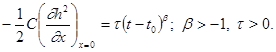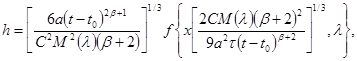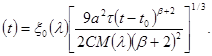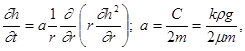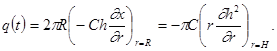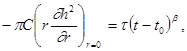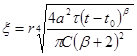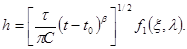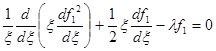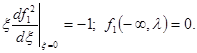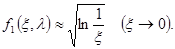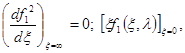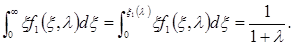Исследования показали, что хотя при установившейся фильтрации газа и происходит понижение температуры, оно относительно невелико даже при больших перепадах давления. Во многих случаях можно принимать для практических целей, что установившаяся фильтрация газа в пористых породах совершается в условиях изотермического изменения его состояния.
1. Дифференциальное уравнение установившейся фильтрации идеального газа.
Как было сказано ранее, для вывода дифференциального уравнения необходимо совместное решение уравнения неразрывности потока, уравнения движения и уравнения состояния.
Уравнение неразрывности потока:
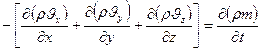
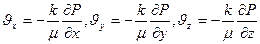
Уравнение состояния идеального газа:
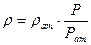
При установившейся фильтрации идеального газа

С учетом (2) – (4) уравнение (1) принимает вид:
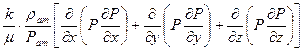
или 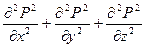
Сравнивая дифференциальное уравнение установившейся фильтрации идеального газа (5) с дифференциальным уравнением установившейся фильтрации несжимаемой жидкости, можно сделать вывод о аналогии, т. е. решения уравнения (5) должны быть аналогичны решениям дифференциального уравнения установившейся фильтрации несжимаемой жидкости. Только вместо Р необходимо брать 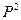
2. Прямолинейно-параллельный поток идеального газа.
Дифференциальное уравнение (5) в этом случае будет иметь вид:
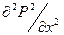
Примем граничные условия:
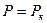
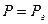
По аналогии с установившимся движением несжимаемой жидкости решение уравнения (6) при условиях (7) дает закон распределения давления в виде:
или 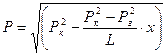
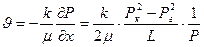
Дебит галереи, приведенный к атмосферному давлению
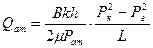
Средневзвешенное по объему пластовое давление
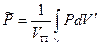
где 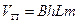

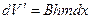
Тогда
После интегрирования получим
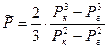
3. Плоскорадиальный фильтрационный поток идеального газа.
Дифференциальное уравнение (5) будет иметь вид:
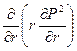
которое решается при следующих граничных условиях
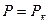
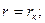
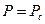
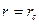
Решение уравнения (13) имеет вид:
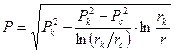
Уравнение (15) представляет собой закон распределения давления в пласте.
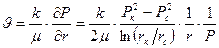
Дебит газовой скважины, приведенный к атмосферному давлению,
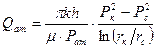
Средневзвешенное по объему пластовое давление определяется по (11) при 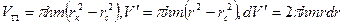

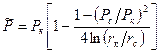
4. Плоскорадиальный фильтрационный поток реального газа по закону Дарси.
Если пластовое давление выше 10МПа и депрессия не слишком мала ( 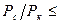
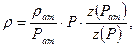
где z – коэффициент сверхсжимаемости газа. Кроме того, для высоких пластовых давлений нужно учитывать зависимость вязкости от давления

или при малых изменениях давления

где µ0 — вязкость при фиксированном давлении;
αµ — коэффициент, определяемый экспериментально и зависящий от состава газа.
Проницаемость пласта принимается постоянной.
Дебит газовой скважины, приведенный к атмосферному давлению,

Имеется несколько способов вычисления интеграла в формуле (22), наиболее употребляем из которых следующий: по графикам зависимостей 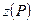

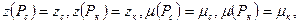
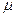
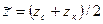
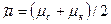
Тогда интеграл в формуле (22) вычисляется и (22) принимает следующий вид:
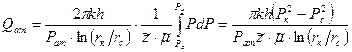
Основная литература: 2 117
Дополнительная литература: 4 71
Контрольные вопросы:
1. Какой газ называется идеальным?
2. Уравнения состояния идеального и реального газов.
3. Дифференциальное уравнение установившейся фильтрации идеального газа.
4. Закон распределения давления при фильтрации идеального газа.
5. Дебит газовой скважины.
6. Средневзвешенное по объему пластовое давление.
7. Коэффициент сверхжимаемости.
8. Зависимость вязкости реального газа от давления.
9. Дебит газовой скважины при фильтрации реального газа.
Дата добавления: 2016-03-10 ; просмотров: 1692 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Двухфазная фильтрация в пористой средеСкачать

Модели пористых сред. Закон Дарси
Вы будете перенаправлены на Автор24
Видео:Раздел 4 Основные модели фильтрацииСкачать

Закон Дарси. Техническая реализация закона. Способы записи закона Дарси
Анри Дарси получил известность благодаря сооружению водопровода в городе Дижон. В 1856 году он смог обосновать закон, который связывал скорость фильтрации жидкости с градиентом давления. В последние годы своей жизни Дарси занимался опытами в области законов движения воды в открытых каналах. Благодаря его исследованиям удалось сделать полезные выводы относительно воздействия профиля русла на коэффициенты сопротивления движению воды.
Закон Дарси – это закономерность фильтрации газов и жидкостей в пористой среде.
Закон Дарси устанавливает линейную зависимость между гидравлическим градиентом (перепад давления, уклон) и объемным расходом газа или жидкости в таких пористых структурах, как:
- Мелкозернистые грунты.
- Глинистые грунты.
- Песчаные грунты.
Данный закон можно выразить через следующую формулу:
Рисунок 1. Формула. Автор24 — интернет-биржа студенческих работ
где, Q — объемный расход жидкости; v — скорость фильтрации жидкости или газа; F — эффективная площадь рассматриваемого объема пористой среды (площадь поперечного сечения образца); k — коэффициент проницаемости пористой среды; р1, р2 — давления, которые созданы на концах испытуемого образца; u — абсолютная вязкость (для жидкости); L — длина фильтрующей части породы.
Коэффициент фильтрации в законе Дарси представляет собой одновременно характеристики среды и жидкости. Значение данного коэффициента зависит от следующих факторов: вязкости жидкости, размер частиц, пористость среды, форма частиц, степень шероховатости. Он применяется, как правило, в гидротехнических расчетах, в которых жидкостью является вода.
Готовые работы на аналогичную тему
При изучении течений газов и жидкостей в пористой среде, в фундаментальной механике сплошных сред, используется дифференциальная форма закона Дарси, которая выглядит следующим образом:
Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ
где, P — внешнее давление; p — плотность флюида; n — динамическая вязкость флюида; g — ускорение свободного падения; z — вертикальная координата; K — коэффициент проницаемости.
Закон Дарси также возможно представить в виде уравнения баланса сил:
Рисунок 3. Формула. Автор24 — интернет-биржа студенческих работ
где, f — поле внешних сил; n — динамическая вязкость газа или жидкости; K = nk / pg — коэффициент проницаемости.
Таким образом, полную систему уравнений фильтрации, включающую условие не сжимаемости, можно записать следующим образом:
Рисунок 4. Система уравнений. Автор24 — интернет-биржа студенческих работ
При условии, что поле скорости фильтрации имеет скалярный потенциал (то есть коэффициент проницаемости постоянен), то закон Дарси можно записать в форме уравнения Лапласа:
Рисунок 5. Уравнение Лапласа. Автор24 — интернет-биржа студенческих работ
Из условия не сжимаемости получается уравнение Лапласа с граничным условием:
Рисунок 6. Уравнение. Автор24 — интернет-биржа студенческих работ
где n — вектор нормали к поверхности.
Техническая реализация закона Дарси происходит при помощи лабораторной установки, использующейся для изучения реальных и модельных характеристики пористых пород. Схема данной установки изображена на рисунке ниже.
Рисунок 7. Схема установки. Автор24 — интернет-биржа студенческих работ
1 — насос с жидкостью или баллон с газом; 2 — вентиль; 3 — регулятор давления; 4 — входной манометр; 5 — модель пористой среды; 6 — выходной манометр; 7 — расходомер.
Закон Дарси используется для расчета фильтрации жидкостей, которые подчиняются закону Навье-Стокса. Для фильтрации некоторых видов нефтей связь между скоростью фильтрации и градиентом давления может быть нелинейной. Для ньютоновских жидкостей применение закона Дарси ограничено маленькими скоростями фильтрации (число Рейнольдса).
Видео:15.10.20 | Фильтрация жидкости в однородной среде со смешанным граничным условиемСкачать

Модели пористых сред
Пористая среда – это твердое тело, пронизанное системой пустот, которые имеют нерегулярный характер и делают среду проницаемой для газов и жидкостей.
Первые исследования порового пространства осуществлялись при помощи идеализированных моделей грунта, называемых:
- Идеальным грунтом.
- Фиктивным грунтом.
Под идеальным грунтом понимается модель пористой среды, каналы которой представляют собой пучки тонких капилляров в виде цилиндров, имеющих параллельные оси. Фиктивный грунт — модель пористой среды, которая состоит из шариков одинакового диаметра. Американский гидрогеолог Слихтер смог упростить теорию фильтрации, что позволило сравнить течение жидкости по порам с движением жидкости по цилиндрическим трубкам. Слихтер, основываясь на модели фиктивного грунта, рассмотрел геометрическую задачу, что позволило связать пористость с углами, которые образованы радиусами соприкасающихся между собой шаров — моделирующих пористую среду, при различной упаковке.
Если объем пустот при воздействии нагрузок не деформируется, то среда – недеформируемая, если деформируется и после снятия нагрузки не восстанавливается, то среда – деформируемая, в случае, если деформируется, но при снятии нагрузки восстанавливается – среда упругая.
Геометрическим параметром, который характеризует размер порового пространства является эффективный диаметр. Данный показатель определяется при помощи механического анализа грунта. Эффективный диаметр, который слагает пористую среду, представляет собой диаметр шаров, которые образовывают фиктивный грунт, в котором гидравлическое давление (оказываемое фильтрующей жидкостью) в эквивалентном и реальном фиктивном грунте одинаково. Эффективный диаметр можно выразить следующей формулой:
Рисунок 8. Формула. Автор24 — интернет-биржа студенческих работ
где, di — средний диаметр i фракции; n — число частиц фракции.
Использование закона Дарси и моделей пористых систем в нефтегазовой промышленности позволяет уже на ранних стадиях проектирования разработки месторождения нефти или природного газа качественно определить основные параметры работы, что будет способствовать техническому и экономическому успеху.
Видео:Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Реферат: Физическое описание явления фильтрации жидкости
| Название: Физическое описание явления фильтрации жидкости Раздел: Рефераты по физике Тип: реферат Добавлен 17:10:55 23 июля 2005 Похожие работы Просмотров: 3226 Комментариев: 21 Оценило: 6 человек Средний балл: 3.7 Оценка: 4 Скачать |
(i , j =1, 2, 3,…) (16)
где компоненты тензора фиктивных напряжений; компоненты тензора истинных напряжений; δij =1 при j =i , δij =0 при i ?j ,
Будучи величинами скалярными, пористость и проницаемость могут зависеть только от инвариантов тензора фиктивных напряжений. Зависимостью их от второго и третьего инвариантов тензорафиктивных напряжений пренебрегают, откуда
где ==- главные нормальные фиктивные напряжения, аq среднее напряжение.
Величину q можно связать с давлением р, если рассматривать напряженные состояние в пласте. Пусть Н — глубина залегания пласта, h-его мощность, а r0 — средняя плотность горных пород. Обыкновенно нефтяные пласты располагаются на значительной глубине под дневной поверхностью и их мощность мала сравнительно с глубиной залегания, т. е. h 3 ), равно по порядку величины
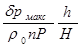
Значение dрмакс /r0 gH обычно не превышает одной-двух десятых; величина h/Н исчезающе мала, так что изменение напряжения во всем вышележащем массиве и, в частности, на его границах мало сравнительно с исходным напряжением. Поэтому можно считать, что при изменении давления жидкости в пласте напряжения, действующие на кровле и подошве пласта, остаются постоянным.
Предыдущее рассуждение существенно основано на том, что модуль Юнга системы жидкость — пористая среда Е и модуль вышележащего массива горных пород Е1 имеют одинаковый порядок величины (что обычно имеет место в действительности). Если бы эти модули Юнга сильно отличались между собой, то выражение (21) содержало бы дополнительный множитель Е1 /Е и при Е1 >> Е отношение напряжений могло бы и не быть малым. Физически это означает, что в случае, когда вышележащая толща сложена из очень жестких пород, могут образоваться своды, и при изменении давления жидкости напряжения на кровле и подошве пласта будут меняться.
Есть теперь пренебречь влиянием таких границ области фильтрации, как стенки скважин (эти границы имеют сравнительно очень малую протяжность; их влияние будет оценено ниже), то из независимости от времени уравнений равновесия системы жидкость — пористая среда (20) и напряжений на кровле и подошве пласта следует важный вывод о независимости суммарного напряженного состояния в системе жидкость — пористая среда от времени, так что
Откуда (22)
Свертывая уравнения (22) (т. е. полагая i, j=1, 2, 3 и суммируя получающие уравнения), имеем
откуда вытекает важное соотношение
2. Основные задачи нестационарной фильтрации
2.1. Уравнение неразрывности
Рассмотрим баланс массы жидкости в произвольном элементе объема пористой среды V, ограниченном поверхностью S. За бесконечно малое время dt приток жидкости внутрь элемента равен согласно определению скорости фильтрации
( единичный вектор нормали; за положительное направление нормали принято направление внешней нормали к поверхности; un — нормальная к поверхности составляющая скорости фильтрации). Приращение массы жидкости внутри этого элемента равняется
откуда в силу произвольности элемента V и вытекает уравнение неразрывности
2.2. Упругий режим фильтрации
1. Самым простым и наиболее изученным случаем нестационарной фильтрации является фильтрации слабосжимаемой жидкости в упругодеформируемом пласте (в технических приложениях эти задачи получили название задач упругого режима фильтрации). В основу исследования кладется система уравнений закона фильтрации и уравнения неразрывности:
Для того чтобы получить замкнутую систему уравнений, нужно воспользоваться тем, что свойства жидкости (плотность r и вязкость m), так же как и пористость и проницаемость пористой среды, являются функциями давления (мы предполагаем движение изотермическим).
В силу (23) имеем
исходя из предположения о слабой сжимаемости жидкости и пористой среды, можно считать относительные изменения величин r и m малыми и коэффициенты при dp/dt в предыдущих формулах постоянными:
Опытные данные показывают, что в реальных случаях
(p-p0 )/Кm 2 , а второй (dp) 2 /L 2 К. Отсюда следует, что вторым членом в принятом приближении также следует пренебречь. Таким образом, имеем
где коэффициент
носит название коэффициента пьезопроводности. Уравнение (29) обычно называется уравнением упругого режима или, по предложению В.Н.Щелкачева, уравнением пьезопроводности. Оно совпадает с хорошо известным классическим уравнением теплопроводности.
2. Рассмотрим постановку основных задач теории упругого режима. Определим распределение давления р в некоторой замкнутой области пространства D на протяжении промежутка времени 0 £ t£ T. Из теории уравнения теплопроводности известно, что если задать на границе Г области D линейную комбинацию давления и его производной по нормали к границе области
и задать начальное распределение давления в области D
то существует распределение давления p(x, y, z, t), и при том единственное, удовлетворяющее уравнению (29), непрерывное в замкнутой области D, включая границу, и удовлетворяющее условия (31) и (32).
Сформулированная задача охватывает почти все основные задачи теории упругого режима фильтрации.
Рассмотрим подробнее физический смысл тех или иных дополнительных условий.
Область, в которой ищется распределение давления жидкости, обычно представляет собой пористый пласт, частично имеющий непроницаемые границы, а частично сообщающиеся с другими пластами и вскрывающими его скважинами. На непроницаемых границах должно удовлетворятся очевидное условие отсутствия потока — равенство нормальной компоненты скорости фильтрации нулю:
откуда, используя закон Дарси, получаем (33)
На участках границы с областями, в которых перераспределения давления практически не происходит (“области питания”), давление можно считать постоянным и известным, так что
Такое условие справедливо, если, например, рассматриваемый пласт граничит с высокопроницаемой областью,
запас жидкости в которой весьма велик. Давление на границе такой области близко к среднему давлению в ней и ввиду ее большого объема мало зависит от процессов, происходящих в исследуемой области. Характерным примером является нефтяная залежь, окруженная со все сторон обширной водоносной областью.
При рассмотрении нестационарных процессов в залежи давление в водоносной области можно считать постоянным. Следует, однако, отчетливо представлять себе, что понятие области постоянного давления не является абсолютным. Чем более длительный характер носят изменения давления, тем на большую область они распространяются.
Часть границы области фильтрации обычно образована стенками скважины или дренажных галерей. На этой части границы чаще всего задается либо давление жидкости, либо поток ее через стенки скважины. Выбор того или иного условия зависит от режима работы скважины или галереи. Могут быть и более сложные условия, когда задается связь с расходом жидкости. Задание потока жидкости согласно закону Дарси эквивалентно заданию нормальной производной от давления.
Условия этого типа выполняются на тех участках границы, через которые может происходить обмен жидкости с соседними пластами через сравнительно слабопроницаемые перемычки. Если толщина перемычки D мала, а давление р¢ за ней можно считать постоянным, то расход вытекающей жидкости через участок перемычки площадью ds составит . Это количество жидкости должно быть равно
где g — замкнутый контур, ограничивающий площадку S, а un — нормальная компонента вектора потока , определяемого соотношением
(x , y , z , t ) = H (x , y , z , t ) + O (u z /C ); =C grad H + O (uz ).
Таким образом, скорость можно, пренебрегая малыми величинами, вынести из-под знака интегрирования по вертикали в соотношении (42), определяющем вектор Тогда получаем
= – Сh grad H . (45)
Представляя (45) в (44), имеем
В это уравнение следует подставить соотношение
определяющее вертикальную координату свободной поверхности Н через ее расстояние h до водоупора и расстояние h0 от водоупора до плоскости отсчета z = 0; получим окончательное уравнение для определения h . В частности, если поверхность водоупора представляет собой горизонтальную плоскость, то ее можно принять за плоскость отсчета и, следовательно, h 0 (x ,y ) можно считать равным нулю. Тогда Н = h , и уравнение (46) принимает вид:
Уравнения (46) и (47) были даны Буссинеском.
2.4. Основные уравнения фильтрации газа
При исследовании фильтрации газа основное значение имеет тот факт, что сжимаемость газа обычно на несколько порядков превышает сжимаемость пористой среды. С учетом этого обстоятельства в уравнении неразрывности
изменением пористости m во времени можно пренебречь, так что получим
Для того чтобы получить замкнутую систему уравнений, снова нужно использовать связь плотности газа r с его давлением р и температурой Т:
поэтому в задаче появляется новая переменная Т, и для замыкания системы уравнений нужно добавить еще одно уравнение — уравнение энергии. Однако, если в среде отсутствуют источники выделения или поглощения энергии, то изменения температуры в процессе движения газа крайне малы, и при расчете поля давления газа ими можно пренебречь. Это обстоятельство легко понять, если учесть, во-первых, крайнюю малость скорости фильтрации и, во-вторых, наличие теплового балласта — скелета пористой среды, эффективно подавляющего изменения температуры. Будем поэтому считать, что
где Т0 — постоянная температура.
Присоединяя к уравнениям (49) и (51) уравнение закона фильтрации (предполагаемого линейным)
получаем замкнутую систему уравнений. Исключая скорость фильтрации, имеем
В уравнении (53) r — известная функция давления. Аналогично и вязкость газа, зависящая в общем случае от давления и температуры, может быть представлена в виде:
Таким образом, и вязкость может считаться известной функцией одного лишь давления.
Введем теперь функции
Уравнение (53) принимает при этом вид:
Можно показать, что уравнение для давления сохранит форму (56) и в случае, если учитывается деформируемость пористой среды, т. е. зависимость от давления пористости и проницаемости (среда по-прежнему считается однородной).
В простейшем случае, когда газ можно считать термодинамически идеальным, с вязкостью, не зависящей от давления,
и уравнение (56) преобразуется к виду:
Уравнения (59) и (60) выведены в предположении постоянства температуры газа Т0 . Поэтому их обычно называют уравнениями изотермической фильтрации газа.
Уравнение (60) — основное для теории фильтрации газа — получено впервые Л. С. Лейбензоном, а затем, несколько позднее, в работе Маскета и Ботсета. Преобразования (55) также берет свое начало от работ Л. С. Лейбензона. Далее уравнение (60) совпадает с уравнением Буссинеска (47) для напора при пологих безнапорных фильтрационных движениях. Эта аналогия, впервые обнаруженная Л. С. Лейбензоном, позволяет рассматривать исследование изотермической фильтрации газа и пологих безнапорных движений несжимаемой жидкости как одну задачу.
3. НЕЛИНЕЙНЫЕ ИНВАРИАНТНЫЕ ЗАДАЧИ
ЖИДКОСТЕЙ И ГАЗОВ
3.1. Общая характеристика инвариантных задач
теории нестационарной фильтрации.
Автомодельные пологие безнапорные движения
при нулевом начальном уровне жидкости
3.3.1. Общая характеристика инвариантных задач теории нестационарной фильтрации. В разделе 2 было показано, что основные задачи гидродинамической теории нестационарной фильтрации приводят к краевым, смешанным или начальным задачам для нелинейных, как правило, дифференциальных уравнений в частных производных параболического типа. Нелинейность вообще характерна для многих актуальных задач современной гидродинамики: газодинамики, теории волн, теории движений вязкой жидкости и т. д. В настоящее время существует сколько-нибудь общих эффективных аналитических методов решения достаточно широких классов нелинейных задач математической физики; это в полной мере относится и к теории фильтрации. Поэтому в теории фильтрации уже давно привлекли внимание своеобразные частные решения, которые выражаются через функции одной переменной. Вначале эти решения обратили на себя внимание только потому, что их получение сводилось к решению обыкновенных уравнений и представлялось (особенно в домашинную эру) более простым, чем решение уравнений в частных производных в общем случае. При построении различных приближенных методов решения, более общих, эти решения часто использовались как эталоны, позволяющие оценить точность метода. (Приближенные методы аналитического решения сохраняют, особенно в теории фильтрации, свое значение и сейчас, при широком внедрении машин, поскольку эти методы дают аналитические формулы, позволяющие наглядно проследить влияние различных параметров, а высокая точность в теории фильтрации не представляет особого интереса. В ряде случаев задачи, описываемые такими решениями, представляют и самостоятельный интерес.
Однако главная ценность таких решений была осознана позднее. Оказалось, что они представляют собой асимптотические представления решений весьма широких классов задач именно там, где детальная структура граничных и начальных условий перестает быть существенной, а эти области часто бывают наиболее интересными (например, спустя некоторое время после начала отбора из скважины, пока воронка депрессии не достигла области влияния соседней скважины и т. д.). Поэтому, зная такие решения, мы фактически получаем возможность судить, по крайней мере качественно, о поведении очень широкого класса фильтрационных движений.
Важным свойством рассматриваемых ниже решений является их инвариантность: для одних из этих решений — “автомодельных” — распределение давлений, напоров, плотностей и т. п. оказывается все время подобным самому себе, для других — перемещается как твердое тело с постоянной скоростью и т. д. Это свойство связано с особым характером задач, приводящих к таким решениям. Выполнение определенных преобразований зависимых и независимых переменных оставляет уравнения, граничные и начальные условия задачи неизменными. Как говорят в математике, эти задачи инвариантны относительно некоторой группы непрерывных преобразований. Такие задачи называются инвариантными, они рассматриваются ниже.
3.1.2. Автомодельные пологие безнапорные движения при нулевом начальном уровне жидкости. Ниже будут рассмотрены точные решения некоторых линейных задач нестационарной фильтрации, характеризующихся нулевым начальным условием. Исследование этого класса движений представляет, помимо непосредственного, также принципиальный интерес, поскольку в подобных задачах наиболее сильно проявляется существенно нелинейный характер рассматриваемой проблемы и обнаруживаются некоторые свойства нелинейных движений, резко отличающие их от соответствующих линейных задач и неизбежно утрачиваемые при линеаризации.
Будем рассматривать безнапорные пологие фильтрационные движения в первоначально сухом грунте, имея в виду, что в силу обнаруженной Л. С. Лейбензоном аналогии все результаты непосредственно переносятся на задачи изотермической фильтрации газа. Излагаемые ниже в этом параграфе решения были получены Г. И. Баренблаттом.
Рассмотрим полубесконечный пласт, имеющий снизу плоскую горизонтальную непроницаемую границу — водоупор, а со стороны канала — плоскую вертикальную границу, перпендикулярную оси x и проходящую через точку x =0.
Пусть начальный напор жидкости в пласте равен нулю, а напор на вертикальной границе пласта изменяется по степенному закону, начиная с исходного момента t =t 0 :
где s > 0, а a — некоторая константа, которую будем выбирать в пределах –Ѕ -1 L 2 T -1 ; [t — t0 ] = T; [x] = L; [s] = [h] T — a , (64)
где через [h], L и Т обозначены соответственно размерности напора, длины и времени; константа a безразмерна. Из аргументов, от которых зависит напор жидкости, можно составить только две независимые безразмерные комбинации:
В силу p- теоремы анализа размерностей выражение для напора можно представить в виде произведения комбинации определяющих параметров, имеющей размерность напора (в качестве нее можно взять s (t — t0 ) a ), на безразмерную функцию от безразмерных комбинаций (65). Имеем таким образом
где f — безразмерная функция, а параметр l введен вместо параметра a для удобства последующего изложения. Очевидно, что l лежит в интервале -1 2 /dx.
При непрерывной функции f(x) и f ¹ 0 требование непрерывности функции df 2 /dx = 2fdf/dx совпадает с требованием непрерывности производной df/dx. Однако при f = 0 из непрерывности df 2 /dx непрерывность df/dx не вытекает. Напротив, как увидим далее, искомая функция f(x, l) имеет в точке, где f обращается в нуль, разрыв первой производной.
Условие (69) удобнее привести к другому виду. Умножим обе части основного уравнения (62) на х и проинтегрируем по х от нуля до бесконечности. В результате получим
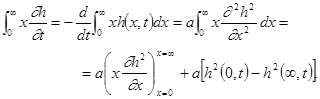
Очевидно, что dh 2 /dx стремится к нулю при х ®¥, быстрее, чем х -1 , в противном случае h не стремилось бы к нулю при х ®¥. Используя это обстоятельство и условие на бесконечности (63), получаем
Интегрируя это соотношение в пределах от t = t 0 до t и используя граничное условие (61) и представление решения (66), имеем
(напомним, что считаем a удовлетворяющим неравенству -1/2
отсюда на основе p- теоремы решение рассматриваемой задачи будет
где j — безразмерная функция.
Положим теперь t = t¢ + t , где t — произвольная константа. При этом условие (72) и уравнение (74), как нетрудно проверить, записываются через новую переменную t¢, так же как и через прежнюю переменную, а условие (73) принимает вид:
Таким образом, сдвиг во времени влияет лишь на некоторое преобразование величины h0 , и постановка задачи оказывается по отношению к группе преобразований переноса по времени; для определения h в переменных х, t¢, a, c, h¢0 получается та же задача, что и для определения h в переменных (75). Стало быть, на основе соотношений (76) и (77) имеем
Отсюда следует, что при любом t имеет место тождество
Положим теперь t = t и получим
Итак, функция h , зависящая от пяти аргументов (75), представляется через функцию одного аргумента:
Подставляя (81) в основное уравнение (74), получаем для функции f (x) обыкновенное дифференциальное уравнение
Подставляя выражение (81) в условие на бесконечности (72) и граничное условие (73), имеем граничные условия для функции f (x):
В силу непрерывности напора жидкости и потока жидкости функция f(x) по-прежнему должна быть непрерывной и иметь непрерывную производную от квадрата df 2 /dx. Мы получили, таким образом, для определения функции f(x) граничную задачу того же типа, что и граничные задачи для автомодельных решений, рассмотренных в предыдущем параграфе, и соответствующую значению параметра a, равному бесконечности, т. е. l = 1. Функция f(x) = f(x, 1) тождественно равна нулю при x ³ x0 = 1,810; передний фронт х0 (t) перемещается, таким образом, по закону
а скорость его перемещения равна
Полученное решение является в некотором смысле предельным для автомодельных решений, рассмотренных выше. В самом деле, положим в формуле (66)
где h0 — константа размерности напора; t — константа размерности времени, причем, очевидно, эти константы выбираются с точностью до некоторого постоянного множителя. Решение (66) принимает вид
Будем неограниченно увеличивать в этом решении a при начальном моменте t0 ® — ¥ по закону
Раскрывая неопределенность, получаем, что при a ® ¥
Уравнение (67) в пределе при a ® ¥ переходит в уравнение (82), а условия (68) и (69) совпадают с условиями (83); f (x, l) ® f (x, 1) = f (x).
Обозначая t через 1/c, получаем, что при a ® ¥ решение (87) стремится к решению (81). Поэтому решение (81) было названо предельным автомодельным решением. Это решение было получено в работе Г. И. Баренблатта. предельные автомодельные решения представляют и принципиальный интерес в том отношении, что для доказательства автомодельности этих решений уже недостаточно соображений анализа размерности, т. е. недостаточно инвариантности постановки задачи относительно группы преобразования подобия величин с независимыми размерностями, как это было в ранее рассмотренных автомодельных задачах, а требуется дополнительно воспользоваться инвариантностью постановки задачи относительно еще одной группы — группы преобразований переноса по времени.
Приведенные при рассмотрении предельной автомодельной задачи рассуждения носят общий характер и могут применяться во многих других задачах. Очевидно, что предельные автомодельные движения существуют всегда, если система основных уравнений рассматриваемой задачи имеет автомодельные решения обычного степенного типа с произвольным показателем степени (который может принимать сколь угодно большие значения) и инвариантна относительно преобразования переноса соответствующей координаты. Как пример можно указать задачу пограничного слоя в несжимаемой жидкости, а также задачу одномерных неустановившихся движений газа. Полученные для этих задач автомодельные решения, содержащие степенные функции независимых переменных, при предельном переходе, аналогичном проделанному в рассматриваемой задаче теории фильтрации, дают предельные автомодельные решения, полученные Гольдштейном и Станюковичем путем формальной постановки.
Задача. На границе х=0 полубесконечного пласта с непроницаемым горизонтальным водоупором задается поток (расход) жидкости как степенная функция времени
Начальный напор во всем пласте равен нулю.
Решение задачи представляется в виде:
где м (l) =-df 2 (0, l)/dx , а координата переднего фронта жидкости х0 (t) — в виде:
2. Осесимметричные автомодельные движения. При осесимметричных пологих безнапорных движениях жидкости напор жидкости h удовлетворяет уравнению
где r — расстояние рассматриваемой точки пласта от оси симметрии.
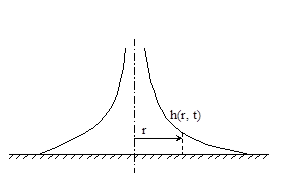
Предположим далее, что расход закачиваемой жидкости изменяется со временем по степенному закону. Выражение для полного расхода жидкости, закачиваемой через скважину радиусом R, имеет вид:
По предположению, радиус скважины пренебрежимо мал (ниже мы остановимся на причинах, по которым это допущение можно делать для большинства реальных движений), поэтому можно принять R = 0; так как расход жидкости, закачиваемой в скважину, меняется по степенному закону, граничное, условие на скважине принимает вид:
где t > 0 и b > -1. В частности, случай b = 0 соответствует закачке жидкости в пласт с постоянным расходом. Таким образом, решение задачи удовлетворяет уравнению (93) и условиям (94) и (96). По-прежнему, используя p- теорему анализа размерности, можно показать, что это решение является автомодельным и представляется в виде:
представляют собой две независимые безразмерные комбинации определяющих параметров решения; других независимых комбинаций этих параметров не существует. Постоянный множитель снова введен в формулу для x с целью удобства последующего изложения. Как и прежде, искомая функция должна быть непрерывной и иметь непрерывную производную от квадрата. Подставляя выражение (77) в уравнение (93) и условия (94) и (96), находим, что функция f1 (x, l) удовлетворяет уравнению
Исследование этой граничной задачи проводится аналогично предыдущему; также единственным образом строится функция f1 (x, l), отличающаяся от нуля лишь при 0 £ x £ x1 (l), где x1 (l) — некоторая функция x, а при x ³ x1 (l) тождественно равная нулю. Функция f1 (x, l) при x®0 имеет особенность, как нетрудно видеть из первого условия (100):
Второе условие (100) может быть приведено к другой форме: умножая уравнение (99) на x и интегрируя в пределах от x = 0 до x = ¥, получаем, используя оба условия (100) и условия
следующее интегральное соотношение:
Первое условие (102) непосредственно следует из условия, которому функция f1 (x, l) на бесконечности, так как если бы предел == при x ® ¥ не был равен нулю, то функция f1 (x, l) не стремилась бы к нулю при x ® ¥. Второе условие (102) непосредственно следует из (101).
Эффективное вычисление функции f1 (x, l) удобно проводить следующим образом. Строим решение задачи Коши Ф1 (x, l) для уравнения (99). обращающееся в нуль при x = 1 и имеющее в этой точке конечную первую производную. Исследование, в точности аналогичное приведенному в п. 3 x1, показывает, что эта производная равна -1/4. Строить решение задачи Коши удобно так: вблизи x = 1 можно представить решение в виде ряда, при помощи которого находится надлежащее число начальных значений, после чего применяется метод численного интегрирования Адамса — Штермера. Далее численно вычисляется величина
🎥 Видео
Особенности фильтрации в трещиноватых и трещиновато-пористых средах {подземная гидрогазодинамика}Скачать

Определение коэффициента фильтрации неуплотненного песчаного грунтаСкачать

Лекция_Проницаемость_Закон_Дарси_09_10_2018Скачать

МОДЕЛИРОВАНИЕ МНОГОФАЗНЫХ ФИЛЬТРАЦИОННЫХ ТЕЧЕНИЙСкачать

Процесс фильтрования | Лекция по ПАППСкачать

Гидродинамика, теплопередача и механика грунтов в COMSOL Multiphysics®. Версия 5.6Скачать

Механика и термодинамика пористой средыСкачать

Закон БернуллиСкачать

К.Д.Толстыгин «Сравнение метода поро-сетевых моделей и уравнения ван Генухтена-Муалема»Скачать

Подземная гидромеханика Лекция 9 Ильдар ИбрагимовСкачать

Супер ЖЕСТЬ для продвинутых: sqrt(2+sqrt(2-sqrt(2+x)))=xСкачать

Вязкость и течение Пуазёйля (видео 14) | Жидкости | ФизикаСкачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Эффект Вентури и трубка Пито (видео 16) | Жидкости | ФизикаСкачать

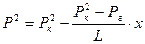


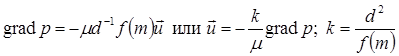

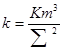
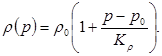
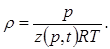
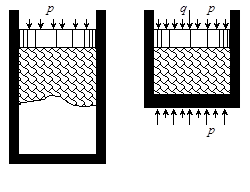 разберем следующую элементарную схему опыта. Пусть в цилиндрическом сосуде с площадью поперечного сечения, равной единице, находится некоторый объем пористой среды, в котором содержится жидкость под давлением p. На верхней грани этого объема лежит непроницаемый поршень, по другую сторону которого находится жидкость под тем же давлением p. В силу известного принципа гидростатики — принципа отвердевания — эта система находится в состоянии равновесия. Для выяснения зависимости пористости от нагрузки приложим к поршню дополнительную нагрузку q. Вычислим сжимающее нормальное напряжение, действующее в сечении объема пористой среды плоскостью, параллельной поршню; для этого составим уравнение равновесия части рассматриваемого объёма, ограниченной поршнем и плоскостью сечения. Пренебрегая силами трения о стенки вмещающего сосуда и собственным весом среды и жидкости, получаем
разберем следующую элементарную схему опыта. Пусть в цилиндрическом сосуде с площадью поперечного сечения, равной единице, находится некоторый объем пористой среды, в котором содержится жидкость под давлением p. На верхней грани этого объема лежит непроницаемый поршень, по другую сторону которого находится жидкость под тем же давлением p. В силу известного принципа гидростатики — принципа отвердевания — эта система находится в состоянии равновесия. Для выяснения зависимости пористости от нагрузки приложим к поршню дополнительную нагрузку q. Вычислим сжимающее нормальное напряжение, действующее в сечении объема пористой среды плоскостью, параллельной поршню; для этого составим уравнение равновесия части рассматриваемого объёма, ограниченной поршнем и плоскостью сечения. Пренебрегая силами трения о стенки вмещающего сосуда и собственным весом среды и жидкости, получаем Величину s f будем в дальнейшем называть фиктивным напряжением.
Величину s f будем в дальнейшем называть фиктивным напряжением.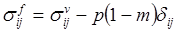
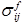
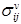
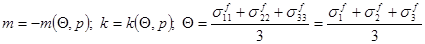
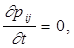
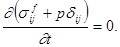
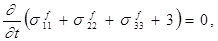
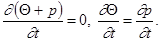
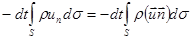
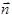
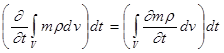
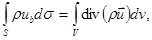
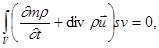
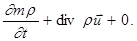

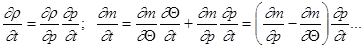
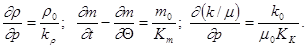

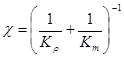

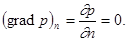
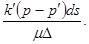
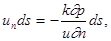
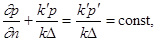
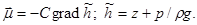


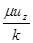
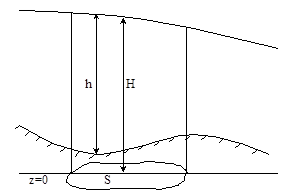 Выведем важное для дальнейших рассуждений соотношение. Рассмотрим объем V, ограниченный свободной поверхностью жидкости и некоторой цилиндрической поверхностью с вертикальными образующими. Обозначим через h расстояние от свободной поверхности жидкости до водоупора, а через H- расстояние от свободной поверхности до горизонтальной плоскости z = 0; очевидно, dh/dt = dH/dt. Объем жидкости, заключенной в объеме V, равен
Выведем важное для дальнейших рассуждений соотношение. Рассмотрим объем V, ограниченный свободной поверхностью жидкости и некоторой цилиндрической поверхностью с вертикальными образующими. Обозначим через h расстояние от свободной поверхности жидкости до водоупора, а через H- расстояние от свободной поверхности до горизонтальной плоскости z = 0; очевидно, dh/dt = dH/dt. Объем жидкости, заключенной в объеме V, равен