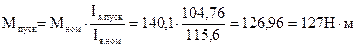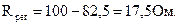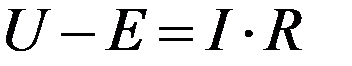В процессе работы генератора постоянного тока в обмотке якоря индуцируется ЭДС Ea. При подключении к генератору нагрузки в цепи якоря возникает ток, а на выводах генератора устанавливается напряжение, определяемое уравнением напряжений для цепи якоря генератора:
сумма сопротивлений всех участков цепи якоря: обмотки якоря ra , обмотки добавочных полюсов rД , компенсационной обмотки rк.о., последовательной обмотки возбуждения и переходного щеточного контакта rщ.
При отсутствии в машине каких-либо из указанных обмоток в (28.2) не входят соответствующие слагаемые.
Якорь генератора приводится во вращение приводным двигателем, который создает на валу генератора вращающий момент М1 Если к генератору не подключена нагрузка (работает в режиме х.х. Ia=0 ), то для вращения его якоря нужен сравнительно небольшой момент холостого хода M0. Этот момент обусловлен тормозными моментами, возникающими в генераторе при его работе в режиме х.х.: моментами от сил трения и вихревых токов в якоре.
При работе генератора с подключенной нагрузкой в проводах обмотки якоря появляется ток, который, взаимодействуя с магнитным полем возбуждения, создает на якоре электромагнитный момент М. В генераторе этот момент направлен встречно вращающему моменту приводного двигателя ПД (рис. 28.1), т. е. он является нагрузочным (тормозящим).
Рис. 28.1. Моменты, действующие в генераторе постоянного тока
При неизменной частоте вращения n = const вращающий момент приводного двигателя M1 уравновешивается суммой противодействующих моментов: моментом х.х. M0 и электромагнитным моментом М, т. е.
Выражение (28.3) —называется уравнением моментов для генератора при постоянной частоте нагрузки. Умножив члены уравнения (28.3) на угловую скорость вращения якоря ω, получим уравнение мощностей:
где P1 = M1ω — подводимая от приводного двигателя к генератору мощность (механическая); P0 = M0ω мощность х.х., т. е. мощность, подводимая к генератору в режиме х.х. (при отключенной нагрузке); PЭМ = Mω— электромагнитная мощность генератора.
Согласно (25.27), получим
или с учетом (28.1)
где P2 — полезная мощность генератора (электрическая), т. е. мощность, отдаваемая генератором нагрузке; PЭa — мощность потерь на нагрев обмоток и щеточного контакта в цепи якоря .
Учитывая потери на возбуждение генератора PЭВ, получим уравнение мощностей для генератора постоянного тока:
Следовательно, механическая мощность, развиваемая приводным двигателем P1, преобразуется в генераторе в полезную электрическую мощность P2, передаваемую нагрузке, и мощность, затрачиваемую на покрытие потерь
Так как генераторы обычно работают при неизменной частоте вращения, то их характеристики рассматривают при условии n = const.
Видео:Электромеханические переходные процессы. Устойчивость. Уравнение движение ротора.Скачать
Рассмотрим основные характеристики генераторов постоянного тока.
Характеристика холостого хода — зависимость напряжения на выходе генератора в режиме х.х. U0 от тока возбуждения IВ:
Нагрузочная характеристика — зависимость напряжения на выходе генератора U при работе с нагрузкой от тока возбуждения IВ:
Внешняя характеристика — зависимость напряжения на выходе генератора U от тока нагрузки I:
Регулировочная характеристика — зависимость тока возбуждения IВ от тока нагрузки I при неизменном напряжении на выходе генератора
Вид перечисленных характеристик определяет рабочие свойства генераторов постоянного тока которые во многом зависят от способа включения генератора в схему, поэтому мы рассмотрим каждый способ включения по отдельности.
Видео:Генератор переменного тока. 11 класс.Скачать

Машины постоянного тока.
Устройство, назначение отдельных частей машины (главные полюсы – создание основного магнитного потока; якорь – индуктируется ЭДС; щёточно-коллекторный аппарат – механический выпрямитель в режиме генератора, перераспределение тока по обмотке якорь-двигатель). Принцип работы в режиме генератора (якорь вращается в неподвижном поле полюсов статора; в проводниках обмотки якоря индуктируется переменная ЭДС 
Связь между ЭДС и напряжением в генераторном 


где Ф, Вб – магнитный поток одного полюса.

где р – число пар полюсов,
а — число пар параллельных ветвей,
N – число проводников якоря.
Генератор – ЭДС, двигатель – противоЭДС.
При n = const и 
Вращающий (двигатель), тормозной (генератор) момент




Электромагнитный момент машины постоянного тока пропорционален току якоря и результирующему потоку каждого полюса.
Уравнение баланса мощностей цепи якоря генератора:

Правая часть уравнения выражает мощность нагрузки и электрические потери мощности в обмотке якоря. Их сумма равна 
Величина 
Для электродвигателя баланс мощностей цепи якоря:

Это уравнение означает, что мощность 


Работа машины постоянного тока сопровождается потерями энергии и нагревом её частей:


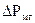

Способы возбуждения машин постоянного тока.

Независимое Последовательное (сериесные)

Параллельное (шунтовые) Смешанное
генераторный: 
двигательный: 
Генераторы с самовозбуждением.
Условия самовозбуждения (наличие остаточного потока, совпадение по направлению 
Двигатели 



Уравнение механической характеристики: 


Из механической характеристики – способы регулирования скорости двигателя:
1) изменение напряжения на якоре U,
2) изменение потока возбуждения Ф,
3) изменение добавочного сопротивления в цепи якоря.
Задача 1.
Генератор независимого возбуждения имеет следующие номинальные данные: 
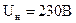


Построить внешнюю характеристику генератора и определить его электромагнитную мощность 
Внешняя характеристика генератора строится по уравнению:


В генераторе независимого возбуждения 
Если пренебречь реакцией якоря, то можно считать


Координаты точек характеристики 



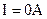

Изменение напряжения на зажимах генератора: 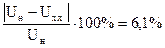
1. Как определяется величина тока генератора независимого возбуждения при режиме К.З.? Опасен ли этот режим для машин?
Величина магнитного потока практически не зависит от нагрузки, следовательно практически постоянной будет и ЭДС генератора. При К.З. U=0, следовательно 

Ток возрастает в 17 раз, что чрезвычайно опасно.
2. Какие причины вызывают уменьшение напряжения генератора при росте нагрузки?
а) при росте нагрузки увеличивается падение напряжения в цепи якоря,
б) хоть и незначительно, изменяется (уменьшается) ЭДС, вследствие реакции якоря.
Задача 2.
На сколько процентов нужно уменьшить магнитный поток генератора постоянного тока с независимым возбуждением и напряжением на выводах 


1) Уравнение электрического равновесия для двух нагрузок:
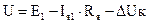

где 

2) В генераторах с независимым возбуждением 



3) Так как ЭДС пропорциональны магнитным потокам, можно записать 
Относительное изменение магнитного потока:




Итак, чтобы напряжение осталось неизменным при уменьшении нагрузки, поток требуется уменьшить на 5,5%.
Задача 3.
Генератор постоянного тока с независимым возбуждением, число полюсов 2р=4, номинальная мощность 


Основные размеры машины: диаметр якоря 


1) Среднюю индукцию воздушного зазора Вб;
2) Полюсное деление 
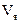
3) число проводников, включённых последовательно в одной ветви обмотки;
4) индуктированную ЭДС;
5) напряжение на выводах генератора и номинальный ток якоря 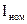
1) Вб – среднее значение индукции на протяжении полюсного деления 


2) Полюсное деление 
Окружная скорость якоря:



3) Число последовательно включённых проводников одной параллельной ветви 
где 2а=2 – число параллельных ветвей при простой волновой обмотке не зависит от числа полюсов и всегда равно 2.
4) ЭДС, индуктированная в якоре 
где Ф – полезный магнитный поток.


5) Уравнение электрического равновесия якорной цепи в номинальном режиме:










Значение 


Дополнительный вопрос.
Машина постоянного тока, рассмотренная в задаче, подключается к сети при напряжении на выводах U=220 В. Ток возбуждения неизменён. Машину в качестве двигателя нагружают до номинальной нагрузки. При этом ток якоря 
Уравнение электрического равновесия в режиме двигателя:




Развиваемый при этом момент 
Задача 4.
Четырёхполюсный генератор постоянного тока вращается с частотой n =1500 об/мин. Диаметр якоря 

1) Построить обмотку так, чтобы она не была ступенчатой;
2) Определить полезный поток машины, если ЭДС Е = 414 В;
3) Определить значение индукции воздушного зазора: среднюю Вб и максимальную Вбmax.
1) Если обмотка не ступенчатая, катушечные стороны располагаются совместно в одном пазу. При этом – пазовый шаг (выражается в количестве зубцовых делений) должен выражаться целым числом.



Число коллекторных пластин k = u·z = 3·43 =129.
Коллекторный шаг 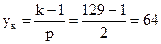
Второй частичный шаг 
Число действующих проводников по периметру якоря: N = 2·u·z·w = 2·3·43·1 = 288.
Схема соединения на рисунке 6.
2) Полезный магнитный поток машины определяется из соотношения 

Средняя индукция воздушного зазора:


Максимальное значение индукции:

Задача 5.
Схема замещения генератора постоянного тока приведена на рис.7.
Uн = 230 В, Iя = 29,6 А, Rя = 0,7 Ом, 
Второй закон Кирхгофа – уравнение электрического состояния генератора 
Номинальный ток возбуждения (закон Ома):

Мощность на нагрузке:

Задача 6.
Условие то же. Построить внешнюю характеристику.
Определить U и Р при I = 24 А.


P = U·I = 232,5·24 = 5580 Вт.
 |  |  |
| 232,5 |
Задача 7.
Характеристика Х.Х. генератора независимого возбуждения задана:
| Е, В | ||
| Iв, А | 1,5 | 4,5 |
Номинальные данные генератора: Рн = 178 кВт, Uн = 230 В, Iян = 775 А, номинальное напряжение на зажимах обмотки возбуждения Uвн = 100 В.
Определить собственное сопротивление обмотки возбуждения Rв, а также сопротивление регулировочного реостата Rp, включаемого в цепь обмотки возбуждения для того, чтобы при неизменном сопротивлении нагрузки R = 0,297 Ом напряжение на её зажимах было равно 
При номинальном режиме 

Согласно характеристике Х.Х. этому значению ЭДС соответствует номинальное значение тока возбуждения Iвн = 4,5 А.
Номинальный режим создаётся при полностью выведенном регулированном реостате. Поэтому собственное сопротивление обмотки возбуждения: 
При снижении напряжения до величины 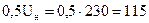

ЭДС обмотки якоря в этом случае определится:

Этому значению ЭДС соответствует на характеристике Х.Х. Iв = 1,55 А. При этом сопротивление цепи возбуждения — 

Сопротивление регулировочного реостата: 
Задача 8.
Генератор постоянного тока с параллельным возбуждением характеризуется следующими номинальными величинами: напряжение Uн, мощность Рн. Мощность потерь в номинальном режиме в % от Рн, в цепи возбуждения Рв.
1) Номинальный ток нагрузки генератора Iн;
2) Номинальный ток возбуждения Iв;
3) Номинальный ток якоря Iя;
4) Сопротивление цепи якоря Rя;
5) ЭДС якоря при токе, равном номинальному;
6) Сопротивление цепи возбуждения при токе возбуждения, равном номинальному;
7) сопротивление обмотки возбуждения, принимая, что при холостом ходе генератора и полностью выведенном реостате в цепи возбуждения ток в этой цепи составляет 1,5Iвн.
При решении воспользоваться зависимостью Е=f(Iв).
| Iв, % |
| Е, % |
| Варианты | Uн, В | Рн, кВт | Ря, % | Рв, % |
| 7,5 | ||||
| 7,5 | ||||
| 6,5 | ||||
| 5,5 | ||||
| 1,5 | ||||
| 4,5 | 1,5 |
Задача 9.
Двигатель постоянного тока параллельного возбуждения включён в сеть U = 110 В, сопротивление обмотки якоря двигателя Rя = 0,07 Ом. При половинной нагрузке частота вращения двигателя n = 1400 об/мин, якорный ток Iя = 74 А. Определить частоту вращения двигателя, если в цепь якоря включено внешнее добавочное сопротивление Rдоб = 0,3 Ом, а нагрузочный момент увеличился вдвое. При этом пренебречь реакцией якоря, а падение напряжения на щётках считать равным 
Момент двигателя постоянного тока 



Уравнение электрического равновесия:




Для второго случая:


Задача 10.
Для тяговых двигателя последовательного возбуждения одинаковой конструкции нагружаются поочерёдно. Напряжение сети U = 500 В. В начале к сети подключается один из этих двигателей и нагружается до тех пор, пока его частота вращения не достигнет n1 = 700 об/мин. Потребляемый из сети ток этого двигателя равен Iя1 = 50 А. Затем то же самое проделывают со вторым двигателем. При той же частоте вращения потребляемый из сети ток Iя2 = 55 А. Внутренне сопротивление цепи якоря каждого двигателя Rя = 0,3 Ом. Валы двух двигателей соединены муфтой. Их электрические цепи соединены последовательно и подключены к сети U = 500 В. Затем оба двигателя нагружаются до тех пор, пока потребляемый ток достигнет значения 
Какова частота вращения машин и в каком соотношении находятся их потребляемые мощности? Предположим, что магнитная цепь машин не насыщена и при малых изменениях магнитный поток изменяется пропорционально току.
Определим индуктированные ЭДС двигателей при их раздельном испытании.





При последовательном включении двигателей:
По условию задачи, магнитный поток изменяется пропорционально току. Так как 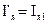

Поток второго двигателя определён из соотношения:




Определяем напряжение на выводах каждого двигателя:


Отношение потребляемых мощностей:

Задача 11.
Двигатель постоянного тока параллельного возбуждения имеет следующие номинальные данные: Рн = 12 кВт, Uн = 220 В, nн = 685 об/мин, Iн = 64 А, Iвн = 1,75 А. Сопротивление обмотки якоря в нагретом состоянии Rя = 0,281 Ом.
Определить скорость вращения якоря двигателя при Х.Х. и тормозном моменте на валу, равном 0,6Мн. Поострить естественную механическую характеристику. Размагничивающим действием реакции якоря пренебречь.
Скорость вращения якоря в режиме идеального Х.Х., когда Uн = Ео, 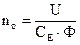


Соотношение токов – по схеме по ходу решения.
Условие динамического равновесия при работе двигателя: 


Вращающий момент пропорционален току якоря. При постоянном магнитном потоке (реакцией якоря пренебрегаем) вращающий момент изменяется вследствие соответствующего изменения тока якоря. Следовательно, при


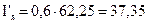
Записываем выражения, определяющие скорости при 



Взяв отношение этих скоростей, получим:

Механическая характеристика n = f(М). Для рассматриваемого двигателя – это прямая линия. Строим по двум точкам: М = 0, n = no = 740 об/мин. М = 0,6Мвр.ном, 
Естественная механическая характеристика – в цепи якоря отсутствует добавочное сопротивление.
1. Составить уравнение баланса мощностей для двигателя в номинальном режиме.


220·62,25 = 202,5·62,25 + 62,25·0,281;
13695 = 12605,6 + 1088,9;
2. Какое дополнительное сопротивление R следует включить в цепь якоря двигателя, чтобы при М = 0,6Мн скорость его вращения снизилась до 630 об/мин?
Соотношение аналогично тому, при котором определилось 


При введении в цепь якоря R получим искусственную механическую характеристику (график).
3. Определить мощность потерь в регулировочном сопротивлении
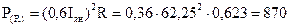
Задача 12.
Двигатель постоянного тока с независимым возбуждением, компенсированный (магнитный поток постоянен), номинальная мощность Рном = 22 кВт, число полюсов 2р = 4, напряжение на выводах U = 220 В, номинальная частота вращения n = 1500 об/мин, КПД 
1) Рассчитать естественную механическую характеристику, считая сопротивление якорной цепи Rя, рассчитать искусственную механическую характеристику при добавочном сопротивлении в цепи якоря Rдоб = 2 Ом;
2) Определить добавочное сопротивление, включаемое последовательно с якорной цепью, для номинального момента, чтобы получить n = 900 об/мин;
3) Определить, насколько нужно уменьшить напряжение на выводах, если необходимо установить n = 900 об/мин при номинальном моменте;
4) Определить, насколько нужно увеличить сопротивление цепи возбуждения, чтобы частота вращения стала равной = 1600 об/мин при номинальном моменте. Характеристика холостого хода машины приведена в виде таблицы
 | 206,5 | ||
 | 0,5 | 1,5 | 2,2 |
1) Механическая характеристика двигателя – это зависимость частоты вращения от момента n = f(M).
Если считать поток постоянным и пренебречь падением напряжения на щётках, то

Получим уравнение прямой, наклон которой к горизонтальной оси определяется величиной m. Теоретически при идеальном холостом ходе Iя = 0 и 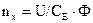
Итак, 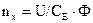



nх = 1583, М = 0 – точка Х.Х. естественной механической характеристики (рис. 8).
Вторая точка – определяется номинальным режимом
Мном = 
На графике – естественная механическая характеристика – 1.
Для искусственной механической характеристики первая точка – точка холостого хода.
Вторую точку можно определить как точку пуска: n = 0, М = Мпуск.

Момент в номинальной точке и пусковой момент: 

На графике – искусственная механическая характеристика 2.
2) Введение добавочного сопротивления в цепь якоря – один из способов регулирования частоты вращения двигателя постоянного тока (уменьшение).
Так регулирование происходит при постоянном моменте, ток якоря в установившемся режиме остаётся неизменным. Если М = Мном, то и Iя = Iя.ном, а поэтому 


125,064 = 220 – 11,56 — Rдоб·115,6,
Механическая характеристика на графике – 3.
Изменение оборотов 

3) Изменение величины питающего напряжения – ещё один способ регулирования частоты вращения двигателя (уменьшение).
Механические характеристики при сохранении неизменным момента в случае уменьшения напряжения сдвигаются параллельно естественной характеристике. При номинальном моменте разность частот вращения 

Для идеального холостого хода:




Итак, напряжение питания надо уменьшить на 83,4 В. Механическая характеристика на графике – 4.
4) Изменение сопротивления цепи возбуждения – ещё один способ изменения скорости вращения двигателя (увеличение).
Уравнение механической характеристики:


Если увеличивается сопротивление цепи возбуждения, ток возбуждения уменьшается, уменьшается и основной поток. Механическая характеристика становится более крутой, частота вращения в режиме холостого хода растёт.
Определим постоянные машины:

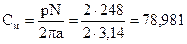
При заданной частоте вращения определим величину магнитного потока:






Выбираем первое решение, так как второе слишком мало для машины с 
Частота вращения при холостом ходе:


На графике – механическая характеристика – 5.
При магнитном потоке 
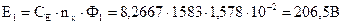
По характеристике холостого хода определяется ток возбуждения: 
Требуемое сопротивление цепи возбуждения:
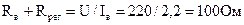
Отсюда
Задача 14.
Электродвигатель постоянного тока с параллельным возбуждением выполнен на номинальное напряжение 220 В. Данные номинального режима электродвигателя: мощность 


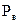
1) номинальный момент на валу электродвигателя;
2) ток 
3) токи в цепи возбуждения и в цепи якоря при номинальной нагрузке;
Видео:Принцип работы генератора переменного токаСкачать

Уравнения электрического равновесия для электрических машин
В процессе работы двигателя его якорь вращается в магнитном поле, при этом в обмотке якоря наводится ЭДС, которая направлена против рабочего тока якоря, поэтому её называют противо ЭДС
В соответствии со вторым законом Кирхгофа электрическое равновесие выглядит следующим образом:
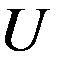
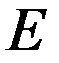
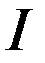
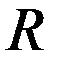
Из второго закона Кирхгофа следует, что подведенное к двигателю напряжение уравновешивается противо ЭДС обмотки якоря и падением напряжения в цепи якоря.
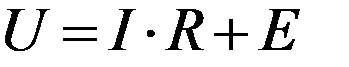
Из формулы (1) видим что ток якоря увеличивается при увеличении питающего напряжения и уменьшения противо ЭДС.
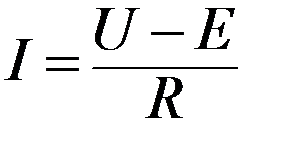
Значение противо ЭДС изменяется прямопропорционально изменению величин конструктивной постоянной машины, магнитного потока полюсов и частоты вращения якоря двигателя.
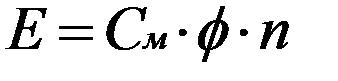
Согласно формулы (3) при трогании с места противо ЭДС Е=0, так как частота вращения якоря двигателя тоже равна нулю n=0 и по этому ток якоря Iя имеет наибольшее значение.
При увеличении скорости движения увеличивается частота вращения якоря ТЭД, следовательно увеличивается значение противо ЭДС, что вызывает уменьшение числителя в формуле (2), т.е. уменьшается ток якоря.
Подставляем значения формулы (3) в Формулу (1) и получаем что:
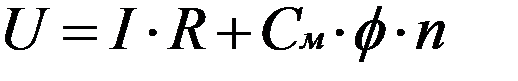
Из формулы (4) определяем значение частоты вращения якоря ТЭД:
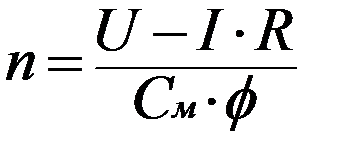
Из формулы (5) видно, что частота вращения якоря двигателя n увеличивается при увеличении подводимого напряжения U, а так же уменьшении магнитного потока 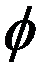
Дата добавления: 2017-06-13 ; просмотров: 2868 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
📹 Видео
Лекция 020-5. Метод эквивалентного генератораСкачать

Урок 356. Генератор переменного электрического токаСкачать

Электрические машины постоянного тока, устройство и принцип действияСкачать

генератор независимого возбужденияСкачать

11 класс урок №11 Генератор переменного токаСкачать

Метод эквивалентного генератора. Задача 2Скачать

Реактивная мощность за 5 минут простыми словами. Четкий #энерголикбезСкачать

Задача 1. Генератор постоянного тока параллельного возбужденияСкачать

Тема: "Генераторы последовательного, параллельного, смешанного возбуждения"Скачать

Схема двигателя постоянного тока. Устройство и принцип работы.Скачать

Математика это не ИсламСкачать

Урок 366. ТрансформаторСкачать

Урок 142 (осн). Решение задачСкачать

2.5. Двигательный режимСкачать

Характиристики машин постоянного токаСкачать

Электрические машины постоянного токаСкачать

Принцип работы трансформатораСкачать