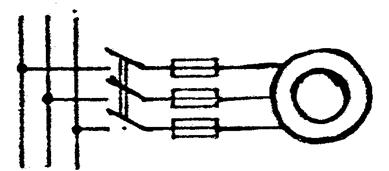
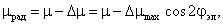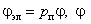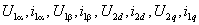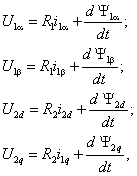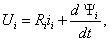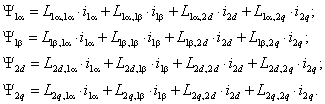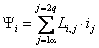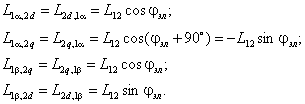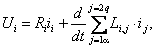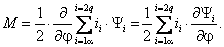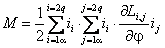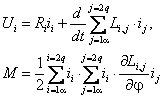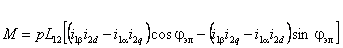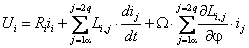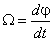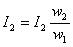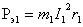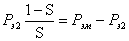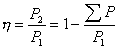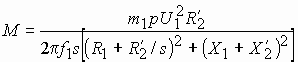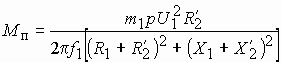2.5. Процессы в асинхронной машине
2.5.1. Цепь статора
А) ЭДС статора.
Магнитное поле, создаваемое обмоткой статора, вращается относительно неподвижного статора с частотой n0=60f)/pи будет наводить в обмотке статора ЭДС. Действующее значение ЭДС, наводимой этим полем в одной фазе обмотки статора определяется выражением:
где: k1=0.92÷0.98– обмоточный коэффициент;
f1=f– частота сети;
w1– число витков одной фазы обмотки статора;
Φ – результирующее магнитное поле в машине.
Б) Уравнение электрического равновесия фазы обмотки статора.
Это уравнение составлено по аналогии с катушкой с сердечником, работающей на переменном токе.

Здесь Ú и Ú1– напряжение сети и напряжение, подведённое к обмотке статора.
R1– активное сопротивление обмотки статора, связанное с потерями на нагрев обмотки.
x1– индуктивное сопротивление обмотки статора, связанное с потоком рассеяния.
z1– полное сопротивление обмотки статора.
İ1– ток в обмотке статора.
При анализе работы асинхронных машин часто принимают I1z1=0. Тогда можно записать:
Из этого выражения следует, что магнитный поток Φ в асинхронной машине не зависит от её режима работы, а при заданной частоте сети fзависит только от действующего значения приложенного напряженияU1. Аналогичное соотношение имеет место и в другой машине переменного тока – в трансформаторе.
Цепь ротора
А) Частота ЭДС и тока ротора.
При неподвижномроторе частота ЭДСf2равна частоте сетиf.
При вращающемсяроторе частота ЭДС ротора зависит от частоты вращения магнитного поля относительно вращающегося ротора, которая определяется соотношением:
Тогда частота ЭДС вращающегося ротора:

Частота ЭДС ротора изменяется пропорционально скольжению и в режиме двигателя имеет наибольшее значение в момент пуска в ход.
Пусть при f=50Гц, номинальное скольжениеSн=2%. Тогда при номинальной частоте вращения ротораf2=f×Sн=1Гц.
Таким образом, в обмотке ротора асинхронной машины частота наводимой ЭДС зависит от частоты вращения ротора.
Б) ЭДС ротора.
При неподвижномротореf2=fи действующее значение ЭДС определяется по аналогии сE1.
где: w2иk2– соответственно число витков и обмоточный коэффициент обмотки ротора.
Если ротор вращается, то f2=f×Sни ЭДСвращающегосяротора определяется соотношением:
ЭДС, наводимая в обмотке ротора, изменяется пропорционально скольжению и в режиме двигателя имеет наибольшее значение в момент пуска в ход.
Отношение ЭДС статора к ЭДС неподвижного ротора называется коэффициентом трансформации асинхронной машины.
| k= | E1 | = | w1k1 | . |
| E2 | w2k2 |
В) ток ротора.
Запишем уравнение равновесия для одной фазы короткозамкнутого ротора.
При неподвижном роторе.

где: x2=2πfL2– индуктивное сопротивление обмотки неподвижного ротора, связанное с потоком рассеяния;
R2– активное сопротивление обмотки ротора, связанное с потерями на нагрев обмотки.
При вращающемся роторе.
Для тока ротора в общем случае можно получить такое соотношение:

Отсюда следует, что ток ротора зависит от скольжения и возрастает при его увеличении, но медленнее, чем ЭДС.
Г) поле ротора
Обмотка ротора, как и обмотка статора, является многофазной и при появлении в ней тока создаёт своё вращающееся магнитное поле. Обозначим через n2частоту вращения магнитного поля ротора относительно ротора.
Здесь p– число пар полюсов обмотки ротора, оно всегда равно числу пар полюсов обмотки статора.
Относительно статора магнитное поле ротора вращается с частотой

Из полученного соотношения следует, что магнитное поле ротора относительно статора вращается с той же частотой, что и магнитное поле статора. Таким образом, магнитные поля ротора и статора относительно друг друга неподвижны. Поэтому при анализе работы асинхронной машины можно применить те же соотношения, что и трансформаторе.
Ток статора
Так как результирующее магнитное поле асинхронной машины не зависит от её режима работы, можно составить для одной фазы уравнение магнитодвижущих сил, приравняв магнитодвижущую силу в режиме холостого хода к сумме магнитодвижущих сил в режиме нагрузки.
Здесь I0– ток в обмотке статора в режиме идеального холостого хода,I’2=−I2(w2k2)/(w1k1) – составляющая тока статора, которая компенсирует действие магнитодвижущей силы обмотки ротора. Полученное выражение для тока статора отражает свойство саморегулирования асинхронной машины. Чем больше ток ротора, тем больше ток статора. В режиме холостого хода ток статора минимальный. В режиме нагрузки ток статора возрастает. Ток реального холостого хода асинхронной машиныI0=(20÷60)%I1ни значительно больше по сравнению с номинальным током, чем у трансформатора. Это объясняется тем, что величина токаI0зависит от магнитного сопротивления среды, в которой создаётся магнитное поле. У асинхронной машины, в отличие от трансформатора, есть воздушный зазор, который создаст большое сопротивление магнитному полю.
К асинхронным машинам полностью применима формула для трансформаторной ЭДС. Пока ротор асинхронного двигателя неподвижен, его обмотка пересекается вращающимся магнитным полем с частотой n1.
где E1—фазное значение ЭДС, наводимой в обмотке статора;E2– фазное значение ЭДС, наводимой в обмотке ротора при неподвижном его состоянии (s= 1;n2= 0);w1, w2—число витков в фазных обмотках статора и ротора;Fm—амплитудное значение магнитного потока фазы асинхронного двигателя;k1,k2—обмоточные коэффициенты статора и ротора асинхронного двигателя.
Обмоточные коэффициенты всегда меньше единицы и в современных асинхронных машинах составляют 0,85 – 0,95. Они обусловлен тем, что в машине переменного тока витки обмотки распределены по внутренней поверхности статора и не одновременно пересекаются магнитным потоком. Поэтому ЭДС отдельных витков сдвинуты по фазе относительно друг друга и складываются не арифметически, как в трансформаторе, а геометрически (рис. 4).
При неподвижном роторе частота индуцируемой в его обмотке ЭДС равна частоте сетиf1. По мере раскручивания ротора скорость (n1–n2) пересечения витков обмотки вращающимся магнитным полем уменьшается, а следовательно, уменьшается частота ЭДС в обмотке ротораf2=p(n1–n2)/60.
Чтобы ввести скольжение в выражение для f2, умножим числитель и знаменатель наn1:
Таким образом, частота ЭДС в обмотке ротора прямо пропорциональна скольжению.
Теперь можно записать выражение для ЭДС обмотки ротора в общем случае:
Следовательно, ЭДС вращающегося ротора(E2s) находится по ЭДС неподвижного ротора умножением его значения на скольжение, соответствующее данной частоте вращения ротора электродвигателя.
Зависимость значения величины и фазы тока от скольжения и от эдс в обмотке ротора
При работе асинхронного двигателя под действием ЭДС (E2s), возникающей во вращающемся роторе, в цепи обмотки ротора возникнет токI2s, который в соответствии с законом Ома для данной цепи найдется из выражения

где Z2s—полное сопротивление фазы ротора;R2—активное сопротивление фазы ротора. Для наиболее широко распространенных двигателейR2считают постоянным и независимым от частоты тока ротора;Х2s— индуктивное сопротивление фазы ротора при заданном скольжении ротораsи частоте тока ротора f2s:X2s=w2L2= 2pf2L2= 2psf1L2=sw1L2, здесьX2= w1L2совпадает с индуктивным сопротивлением обмотки неподвижного ротора. С учетом того, чтоE2s=sE2иX2s= 2pL2f2s=sX2, получим выражение для тока ротора в другом виде:

Из формулы видно, что ток ротора вращающегося двигателя можно определить через ЭДС неподвижного ротора. Индуктивное сопротивление X2, входящее в выражение для тока ротора, соответствует частотеf1и является постоянным, а активное сопротивление электрической цепи ротора при этом зависит от скольжения и находится как отношениеR2/s =R2+R2(1–s)/s.
С учетом вышеприведенного, а также выражения для тока ротора схема замещения вращающегося ротора асинхронного электродвигателя может быть сведена к схеме замещения неподвижного ротора, представленной на рис. 5. Активное сопротивлениеR2(1–s)/sможно рассматривать как внешнее сопротивление, включенное в обмотку неподвижного ротора. В этом случае асинхронный двигатель аналогичен трансформатору, работающему на внешнюю нагрузку, величина сопротивления которого определяется скольжением, а следовательно, механической нагрузкой на валу двигателя. Так, если нагрузочный момент на валу двигателяМ= 0, то скольжениеs= 0. При этомR2(1–s)/s=¥, что соответствует работе двигателя в режиме холостого хода. Если же нагрузочный момент на валу двигателя превышает его вращающий момент, то ротор останавливается (s= 1). При этомR2(1–s)/s= 0, что соответствует режиму короткого замыкания асинхронного двигателя.
При построении схемы замещения асинхронного электродвигателя, параметры схемы замещения ротора, подобно тому, как это делается для вторичной обмотки трансформатора, приводят к числу витков и ЭДС обмотки статора электродвигателя. В результате полная схема замещения асинхронного двигателя имеет вид, представленный на рис. 6.
Магнитная связь обмоток статора и ротора в асинхронном двигателе на схеме замещения заменена электрической связью цепей статора и ротора. Сдвиг фаз между током и ЭДС ротора может быть определен по его схеме замещения (рис. 5).

При неподвижном роторе в момент запуска, когда s= 1, ток и ЭДС ротора сдвинуты по фазе на максимальный угол, 
Схема замещения асинхронного двигателя
При практических расчетах вместо реального асинхронного двигателя, на схеме его заменяют эквивалентной схемой замещения, в которой электромагнитная связь заменена на электрическую. При этом параметры цепи ротора приводятся к параметрам цепи статора.
По сути, схема замещения асинхронного двигателя аналогична схеме замещения трансформатора. Различие в том, что у асинхронного двигателя электрическая энергия преобразуется в механическую энергию (а не в электрическую, как это происходит в трансформаторе), поэтому на схеме замещения добавляют переменное активное сопротивление r2‘(1-s)/s, которое зависит от скольжения. В трансформаторе, аналогом этого сопротивления является сопротивление нагрузки Zн.
Величина скольжения определяет переменное сопротивление, например, при отсутствии нагрузки на валу, скольжение практически равно нулю s≈0, а значит переменное сопротивление равно бесконечности, что соответствует режиму холостого хода. И наоборот, при перегрузке двигателя, s=1, а значит сопротивление равно нулю, что соответствует режиму короткого замыкания.
Как и у трансформатора, у асинхронного двигателя есть Т-образная схемазамещения.
Более удобной при практических расчетах является Г-образная схема замещения.
В Г-образной схеме, намагничивающая ветвь вынесена к входным зажимам. Таким образом, вместо трех ветвей получают две ветви, первая – намагничивающая, а вторая – рабочая. Но данное действие требует внесение дополнительного коэффициента c1, который представляет собой отношение напряжения подводимого к двигателю, к ЭДС статора.
Величина c1 приблизительно равна 1, поэтому для максимального упрощения, на практике принимают значение c1≈1. При этом следует учитывать, что значение коэффициента c1 уменьшается с увеличением мощности двигателя, поэтому более точное приближение будет соответствовать более мощному двигателю.
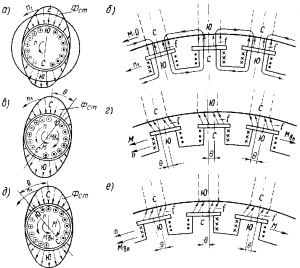
Электромагнитный момент. Электромагнитный момент в синхронном двигателе возникает в результате взаимодействия магнитного потока ротора (потока возбуждения Фв) с вращающимся магнитным полем, создаваемым трехфазным током, протекающим по обмотке якоря (потоком якоря Фв). При холостом ходе машины оси магнитных полей статора и ротора совпадают (рис. 292,а). Поэтому электромагнитные силы I, возникающие между «полюсами» статора и полюсами ротора, направлены радиально (рис. 292, б) и электромагнитный момент машины равен нулю. При работе машины в двигательном режиме (рис. 292, в и г) ее ротор под действием приложенного к валу внешнего нагрузочного момента Мвн смещается на некоторый угол 0 против направления вращения. В этом случае в результате электромагнитного взаимодействия между ротором и статором создаются электромагнитные силы I, направленные по направлению вращения, т. е. образуется вращающий электромагнитный момент М, который стремится преодолеть действие внешнего момента Мвн. Максимум момента Мmax
соответствует углу ? = 90°, когда оси полюсов ротора расположены между осями «полюсов» статора.
Если нагрузочный момент Мвн, приложенный к валу электродвигателя, станет больше Мmax, то двигатель под действием внешнего момента Мвн останавливается; при этом по обмотке якоря неподвижного двигателя будет протекать очень большой ток. Этот режим называется выпаданием из синхронизма, он является аварийным и не должен допускаться.
При работе машины в генераторном режиме (рис. 292, д и е) ротор под действием приложенного к валу внешнего момента Мвн смещается на угол ? по направлению вращения. При этом создаются электромагнитные силы, направленные против вращения, т. е. образуется тормозной электромагнитный момент М. Таким образом, при изменении значения и направления внешнего момента на валу ротора Мвн изменяется лишь угол ? между осями полей статора и ротора, в то время как в асинхронной машине в этом случае изменяется частота вращения ротора.
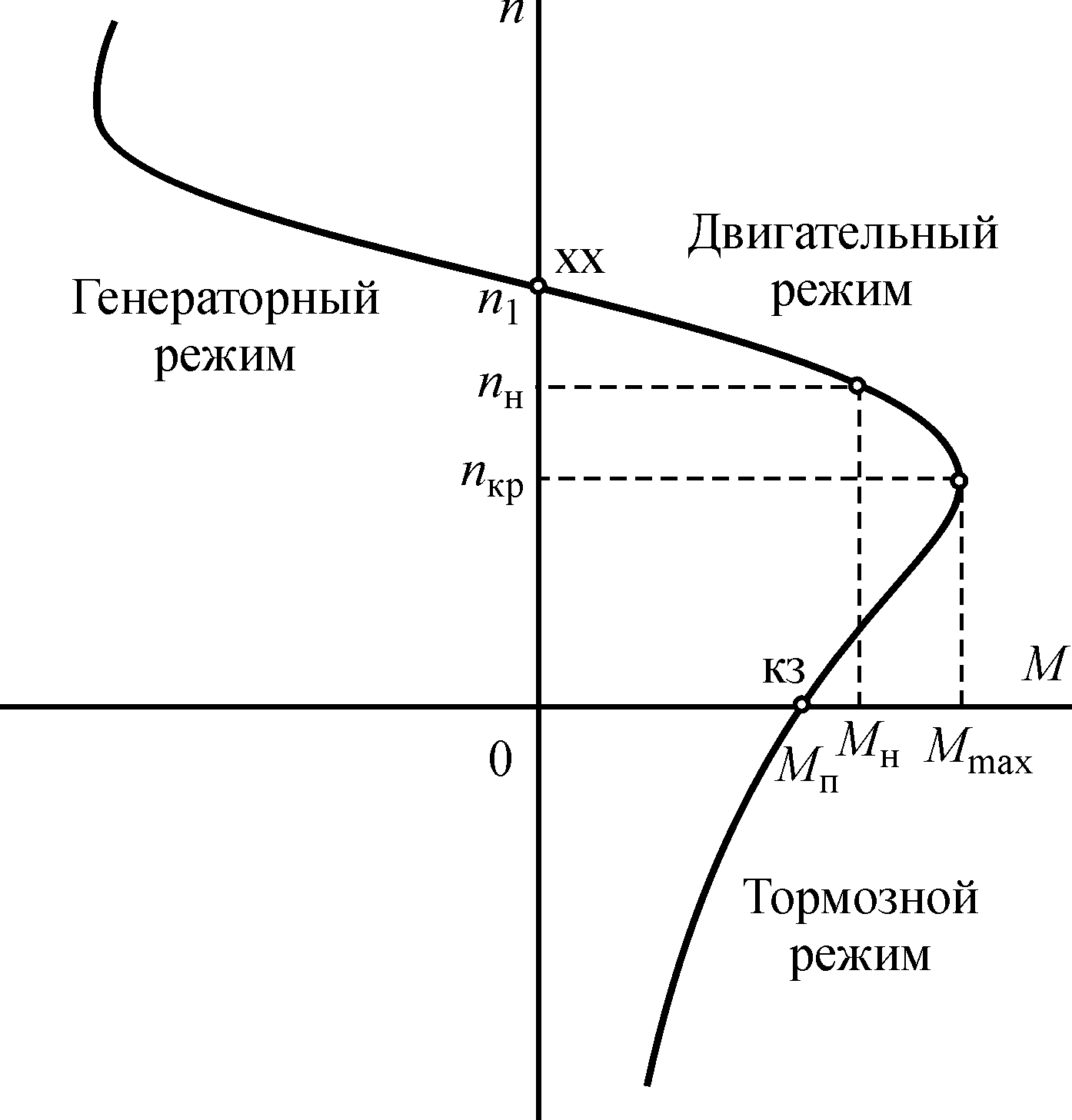
Характеристики асинхронных двигателей. Для правильной эксплуатации асинхронного двигателя необходимо знать его характеристики: механическую и рабочие.
Механическая характеристика. Зависимость частоты вращения ротора от нагрузки (вращающегося момента на валу) называется механической характеристикой асинхронного двигателя (рис. 262, а). При номинальной нагрузке частота вращения для различных двигателей обычно составляет 98—92,5 % частоты вращения n1 (скольжение sном = 2 – 7,5 %). Чем больше нагрузка, т. е. вращающий момент, который должен развивать двигатель, тем меньше частота вращения ротора. Как показывает кривая

на рис. 262, а, частота вращения асинхронного двигателя лишь незначительно снижается при увеличении нагрузки в диапазоне от нуля до наибольшего ее значения. Поэтому говорят, что такой двигатель обладает жесткой механической характеристикой.
Наибольший вращающий момент Mmax двигатель развивает при некоторое скольжении skp, составляющем 10—20%. Отношение Mmax/Mном определяет перегрузочную способность двигателя, а отношение Мп/Мном — его пусковые свойства.
Двигатель может устойчиво работать только при обеспечении саморегулирования, т. е. автоматическом установлении равновесия между приложенным к валу моментом нагрузки Мвн и моментом М, развиваемым двигателем. Этому условию соответствует верхняя часть характеристики до достижения Mmax (до точки В). Если нагрузочный момент Мвн превысит момент Mmax, то двигатель теряет устойчивость и останавливается, при этом по обмоткам машины будет длительно проходить ток в 5—7 раз больше номинального, и они могут сгореть.
При включении в цепь обмоток ротора пускового реостата получаем семейство механических характеристик (рис. 262,б). Характеристика 1 при работе двигателя без пускового реостата называется естественной. Характеристики 2, 3 и 4, получаемые при подключении к обмотке ротора двигателя реостата с сопротивлениями R1п (кривая 2), R2п (кривая 3) и R3п (кривая 4), называют реостатными механическими характеристиками. При включении пускового реостата механическая характеристика становится более мягкой (более крутопадающей), так как увеличивается активное сопротивление цепи ротора R2 и возрастает sкp. При этом уменьшается пусковой ток. Пусковой момент Мп также зависит от R2. Можно так подобрать сопротивление реостата, чтобы пусковой момент Мп был равен наибольшему Мmax.
В двигателе с повышенным пусковым моментом естественная механическая характеристика приближается по своей форме к характеристике двигателя с включенным пусковым реостатом. Вращающий момент двигателя с двойной беличьей клеткой равен сумме двух моментов, создаваемых рабочей и пусковой клетками. Поэтому характеристику 1 (рис. 263) можно получить путем суммирования характеристик 2 и 3, создаваемых этими клетками. Пусковой момент Мп такого двигателя значительно больше, чем момент М’п обычного короткозамкнутого двигателя. Механическая характеристика двигателя с глубокими пазами такая же, как и у двигателя с двойной беличьей клеткой.
Рабочие характеристики.Рабочими характеристиками асинхронного двигателя называются зависимости частоты вращения n (или скольжения s), момента на валу М2, тока статора I1коэффициента полезного действия ? и cos?1, от полезной мощности Р2 = Рmx при номинальных значениях напряжения U1 и частоты f1 (рис. 264). Они строятся только для зоны практической устойчивой работы двигателя, т. е. от скольжения, равного нулю, до скольжения, превышающего номинальное на 10—20%. Частота вращения n с ростом отдаваемой мощности Р2 изменяется мало, так же как и в механической характеристике; вращающий момент на валу М2 пропорционален мощности Р2, он меньше электромагнитного момента М на значение тормозящего момента Мтр, создаваемого силами трения.
Ток статора I1, возрастает с увеличением отдаваемой мощности, но при Р2 = 0 имеется некоторый ток холостого хода I0. К. п. д. изменяется примерно так же, как и в трансформаторе, сохраняя достаточно большое значение в сравнительно широком диапазоне нагрузки.
Наибольшее значение к. п. д. для асинхронных двигателей средней и большой мощности составляет 0,75—0,95 (машины большой мощности имеют соответственно больший к. п. д.). Коэффициент мощности cos?1 асинхронных двигателей средней и большой мощности при полной нагрузке равен 0,7—0,9. Следовательно, они загружают электрические станции и сети значительными реактивными токами (от 70 до 40% номинального тока), что является существенным недостатком этих двигателей.


При нагрузках 25—50 % номинальной, которые часто встречаются при эксплуатации различных механизмов, коэффициент мощности уменьшается до неудовлетворительных с энергетической точки зрения значений (0,5—0,75).
При снятии нагрузки с двигателя коэффициент мощности уменьшается до значений 0,25—0,3, поэтому нельзя допускать работу асинхронных двигателей при холостом ходе и значительных недогрузках.
Вопрос
Работа при пониженном напряжении и обрыве одной из фаз.
Понижение напряжения сети не оказывает существенного влияния на частоту вращения ротора асинхронного двигателя. Однако в этом случае сильно уменьшается наибольший вращающий момент, который может развить асинхронный двигатель (при понижении напряжения на 30% он уменьшается примерно в 2 раза). Поэтому при значительном падении напряжения двигатель может остановиться, а при низком напряжении — не включиться в работу.
На э. п. с. переменного тока при уменьшении напряжения в контактной сети соответственно уменьшается и напряжение в трехфазной сети, от которой питаются асинхронные двигатели, приводящие во вращение вспомогательные машины (вентиляторы, компрессоры, насосы). Для того чтобы обеспечить нормальную работу асинхронных двигателей при пониженном напряжении (они должны нормально работать при уменьшении напряжения до 0,75Uном), мощность всех двигателей вспомогательных машин на э. п. с. берется примерно в 1,5—1,6 раза большей, чем это необходимо для привода их при номинальном напряжении. Такой запас по мощности необходим также из-за некоторой несимметрии фазных напряжений, так как на э. п. с. асинхронные двигатели питаются не от трехфазного генератора, а от расщепителя фаз. При несимметрии напряжений фазные токи двигателя будут неодинаковы и сдвиг между ними по фазе не будет равен 120°. В результате по одной из фаз будет протекать больший ток, вызывающий увеличенный нагрев обмоток данной фазы. Это заставляет ограничивать нагрузку двигателя по сравнению с работой его при симметричном напряжении. Кроме того, при несимметрии напряжений возникает не круговое, а эллиптическое вращающееся магнитное поле и несколько изменяется форма механической характеристики двигателя. При этом уменьшаются его наибольший и пусковой моменты. Несимметрию напряжений характеризуют коэффициентом несимметрии, который равен среднему относительному (в процентах) отклонению напряжений в отдельных фазах от среднего (симметричного) напряжения. Систему трехфазных напряжений принято считать практически симметричной, если этот коэффициент меньше 5 %.
При обрыве одной из фаз двигатель продолжает работать, но по неповрежденным фазам будут протекать повышенные токи, вызывающие увеличенный нагрев обмоток; такой режим не должен допускаться. Пуск двигателя с оборванной фазой невозможен, так как при этом не создается вращающееся магнитное поле, вследствие чего ротор двигателя не будет вращаться.
Использование асинхронных двигателей для привода вспомогательных машин э. п. с. обеспечивает значительные преимущества по сравнению с двигателями постоянного тока. При уменьшении напряжения в контактной сети частота вращения асинхронных двигателей, а следовательно, и подача компрессоров, вентиляторов, насосов практически не изменяются. В двигателях же постоянного тока частота вращения пропорциональна питающему напряжению, поэтому подача этих машин существенно уменьшается.
Пусковые свойства двигателей.
При пуске ротор двигателя, преодолевая момент нагрузки и момент инерции, разгоняется от частоты вращения п = 0 до п . Скольжение при этом меняется от sп = 1 до s. При пуске должны выполняться два основных требования: вращающий момент должен бить больше момента сопротивления (Мвр>Мс) и пусковой ток Iп должен быть по возможности небольшим.
В зависимости от конструкции ротора (короткозамкнутый или фазный), мощности двигателя, характера нагрузки возможны различные способы пуска: прямой пуск, пуск с использованием дополнительных сопротивлений, пуск при пониженном напряжении и др. Ниже различные способы пуска рассматриваются более подробно.
Прямой пуск. Пуск двигателя непосредственным включением на напряжение сети обмотки статора называется прямым пуском. Схема прямого пуска приведена на рис. 3.22. При включении рубильника в первый момент скольжение s = l, а приведенный ток в роторе и равный ему ток статора

максимальны (см.п.3.19 при s=1). По мере разгона ротора скольжение уменьшается и поэтому в конце пуска ток значительно меньше, чем в первый момент. В серийных двигателях при прямом пуске кратность пускового тока kI = IП / I1НОМ = ( 5,…,7), причем большее значение относится к двигателям большей мощности.
Значение пускового момента находится из (3.23) при s = 1:
.(3.38)
Из рис. 3.18 видно, что пусковой момент близок к номинальному и значительно меньше критического. Для серийных двигателей кратность пускового момента МП/ МНОМ = (1.0,…,1.8).
Приведенные данные показывают, что при прямом пуске в сети, питающей двигатель, возникает бросок тока, который может вызвать настолько значительное падение напряжение, что другие двигатели, питающиеся от этой сети, могут остановиться. С другой стороны, из-за небольшого пускового момента при пуске под нагрузкой двигатель может не преодолеть момент сопротивления на валу и не тронется с места. В силу указанных недостатков прямой пуск можно применять только у двигателей малой и средней мощности (примерно до 50 кВт).
Пуск двигателей с улучшенными пусковыми свойствами. Улучшение пусковых свойств асинхронных двигателей достигается использованием эффекта вытеснения тока в роторе за счет специальной конструкции беличьей клетки. Эффект вытеснения тока состоит в следующем: потокосцепление и индуктивное сопротивление X2 проводников в пазу ротора тем выше, чем ближе ко дну паза они расположены (рис.3.23). Также X2 прямо пропорционально частоте тока ротора.
Следовательно, при пуске двигателя, когда s=1 и f2 = f1 = 50 Гц , индуктивное сопротивление X2 = max и под влиянием этого ток вытесняется в наружный слой паза. Плотность тока j по координате h распределяется по кривой, показанной на рис.3.24. В результате ток в основном проходит по наружному сечению проводника, т.е. по значительно меньшему сечению стержня, и, следовательно, активное сопротивление обмотки ротора R2 намного больше, чем при нормальной работе. За счет этого уменьшается пусковой ток и увеличивается пусковой момент МП (см. (3.37), (3.38) ). По мере разгона двигателя скольжение и частота тока ротора падает и к концу пуска достигает 1 – 4 Гц. При такой частоте индуктивное сопротивление мало и ток распределяется равномерно по всему сечению проводника. При сильно выраженном эффекте вытеснения тока становится возможным прямой пуск при меньших бросках тока и больших пусковых моментах.
К двигателям с улучшенными пусковыми свойствами относятся двигатели, имеющие роторы с глубоким пазом, с двойной беличьей клеткой и некоторые другие.
Двигатели с глубокими пазами. Как показано на рис.3.25, паз ротора выполнен в виде узкой щели, глубина которой примерно в 10 раз больше, чем ее ширина. В эти пазы-щели укладывается обмотка в виде узких медных полос. Распределение магнитного потока показывает, что индуктивность и индуктивное сопротивление в нижней части проводника значительно больше, чем в верхней части. Поэтому при пуске ток вытесняется в верхнюю часть стержня и активное сопротивление значительно увеличивается. По мере разгона двигателя скольжение уменьшается, и плотность тока по сечению становится почти одинаковой. В целях увеличения эффекта вытеснения тока глубокие пазы выполняются не только в виде щели, но и трапецеидальной формы. В этом случае глубина паза несколько меньше, чем при прямоугольной форме.
Двигатели с двойной клеткой. В таких двигателях обмотки ротора выполняются в виде двух клеток (рис.3.26): во внешних пазах 1 размещается обмотка из латунных проводников, во внутренних 2 – обмотка из медных проводников. Таким образом, внешняя обмотка имеет большее активное сопротивление, чем внутренняя. При пуске внешняя обмотка сцепляется с очень слабым магнитным потоком, а внутренняя – сравнительно сильным полем. В результате ток вытесняется во внешнюю клетку, а во внутренней тока почти нет.
По мере разгона двигателя ток из внешней клетки переходит во внутреннюю и при s =sНОМ протекает в основном по внутренней клетке. Ток во внешней клетке при этом сравнительно небольшой. Результирующий пусковой момент, складывающийся из моментов от двух клеток, значительно больше, чем у двигателей нормальной конструкции, и несколько больше, чем у двигателей с глубоким пазом. Однако следует иметь в виду, что стоимость двигателей с двойной клеткой ротора выше.
Видео:Как выучить Химию с нуля за 10 минут? Принцип Ле-ШательеСкачать

Уравнения электрического равновесия для фазы статора
Тема: «Краткие сведения из теории обобщенной электрической машины»
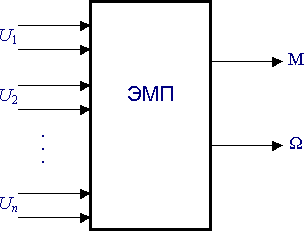
Рассматривая двигатель как элемент электромеханической системы, целесообразно механическую инерцию ротора и момент потерь на его валу отнести к механической части системы, считая механическими переменными электромагнитный момент двигателя М и скорость его ротора 
Рис. 2.1. Электромеханический многополюсник
Этому условию соответствует представление двигателя в виде электромеханического многополюсника [2] (рис. 2.1), имеющего пар электрических зажимов, соответствующих обмоткам двигателя, к которым подведены напряжения u1, u2, , un, и одну пару механических зажимов, представляющих безынерционный ротор двигателя, на котором при скорости 
Переменные М, 
Для построения математического описания динамических процессов в электродвигательных устройствах любого типа (постоянного и переменного тока) используются элементы теории обобщенной электрической машины [2]. Без ее использования практически невозможно построить модель электродвигателей переменного тока.
Известно [2], что любая многофазная электрическая машина с nфазной обмоткой статора и mфазной обмоткой ротора при условии равенства полных сопротивлений фаз статора (ротора) для изучения динамических процессов может быть представлена эквивалентной двухфазной машиной.
Понятие обобщенной электрической машины
Обобщенная машина является упрощенной моделью реальной машины. Ее отличительными признаками являются:
Сосредоточенные в пазах проводники стоком заменены синусоидальными токовыми слоями, эквивалентными по магнитодинамической силе (МДС) первым гармоникам МДС соответствующих реальных обмоток.
Не учитывается неравномерность воздушного зазора, обусловленная пазами.
Наличие явнополюсной структуры на статоре (роторе) учитывается введением первой гармоники переменной составляющей зазора.
Магнитная цепь имеет очень высокую магнитную проницаемость и не насыщается, то есть считается, что энергия магнитного поля сосредоточена в воздушном зазоре. Влияние явнополюсности учитывается введением переменной радиальной магнитной проницаемости [2]
— соответственно электрической и геометрический угол поворота ротора относительно статора; 
Полные сопротивления фаз статора и ротора равны.
Математическое описание процессов электромеханического преобразования энергии в обобщенной машине
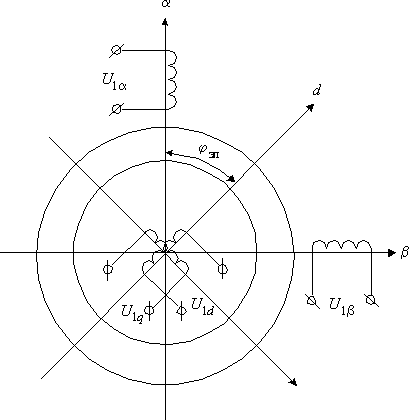
Обобщенная электрическая машина может быть представлена схемой приведенной на рис. 2.2. Две обмотки статора размещены в ортогональной системе координат 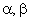
Рис. 2.2. Схема обобщенной машины
Для координат и параметров обобщенной машины будем использовать следующую систему индексов. Индексами 1 и 2 будем обозначать координаты и параметры, относящиеся соответственно к статору и ротору; индексы 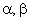
Динамика обобщенной электрической машины описывается четырьмя уравнениями электрического равновесия в цепях ее обмоток и уравнением электромеханического преобразования энергии. Уравнения электрического равновесия, выраженные через потокосцепления, и записанные относительно реальных напряжений и токов статора и ротора
где 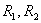
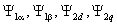
Уравнения (2.2) однотипны и их можно записать в компактной обобщающей форме:
где индекс i принимает значения 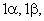
Потокосцепления обмоток в общем виде определяются результирующим действием токов всех обмоток машины:
Здесь для собственных и взаимных индуктивностей обмоток принято одинаковое обозначение с подстрочным индексом, первая часть которого i=

Однотипность записи уравнений (2.4) позволяет в дальнейшем прибегнуть к удобной обобщенной форме записи этой системы
При работе машины взаимное положение обмоток статора и ротора изменяется, поэтому собственные и взаимные индуктивности обмоток в общем случае являются функцией угла поворота ротора
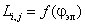
Для симметричной неянополюсной машины собственные индуктивности статора и ротора не зависят от положения ротора
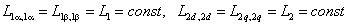
а взаимные индуктивности между обмотками статора или ротора равны нулю
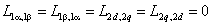
так как магнитные оси этих обмоток сдвинуты в пространстве на угол
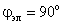
Взаимные индуктивности обмоток статора и ротора проходят полный цикл изменений при повороте ротора на угол
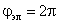
поэтому можно записать
С учетом выражения (2.5) уравнения электрического равновесия можно представить в обобщенной форме записи
где 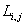
В результате взаимодействия токов, протекающих по обмоткам обобщенной машины, на ее роторе создается электромагнитный момент М, который может быть определен с помощью известных соотношений [2]:
С помощью выражения (2.5) электромагнитный момент может быть выражен через токи обмоток:
Уравнения электрического равновесия (2.7) в сочетании с уравнением электромагнитного момента (2.8) представляют собой математическое описание динамического процесса преобразования энергии, которое в дальнейшем будет конкретизировано для наиболее используемых разновидностей электродвигателей. В обобщенной форме это описание принимает следующий вид:
Уравнение электромагнитного момента можно упростить, подставив в (2.9) выражения для собственных и взаимных индуктивностей обмоток (2.6):
В электрическом двигателе осуществляется связь механического движения привода и приводимого им в движение механизма с электрическими процессами в системе автоматического управления и наоборот. Эта связь объединяет механическую и электрическую части в единую электромеханическую систему.
Так как 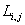
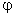
— угловая скорость вала двигателя.
Первый член каждого уравнения (2.12) представляет собой падение напряжения на активном сопротивлении цепи данной обмотки, второй результирующую ЭДС самоиндукции и взаимной индукции 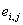
Следовательно, математическое описание процессов преобразования энергии в обобщенной электрической машине в общем виде имеет следующий вид:
Контрольные вопросы к лекции No 2.
Назовите основное условие возможности представления многофазной электрической машины с nфазной обмоткой статора и mфазной обмоткой ротора эквивалентной двухфазной машиной.
С какой скорость вращаются обмотки статора обобщенной электрической машины?
С какой скорость вращаются обмотки ротора обобщенной электрической машины?
Значения каких индуктивностей обмоток статора и ротора от угла поворота ротора 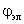
Поясните физический смысл полученных уравнений электрического равновесия напряжений в обмотках обобщенной электрической машины:
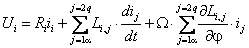
Полные сопротивления фаз статора и ротора должны быть соответственно равны.
Обмотки статора обобщенной электрической машины неподвижны в пространстве.
Обмотки ротора обобщенной электрической машины неподвижны относительно ротора и вращаются в пространстве со скоростью ротора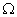
Взаимные индуктивности 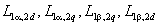
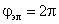
Первый член каждого уравнения представляет собой падение напряжения на активном сопротивлении цепи данной обмотки, второй результирующую ЭДС самоиндукции и взаимной индукции 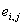
Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Основные уравнения асинхронного двигателя
Напряжение U1, приложенное к фазе обмотки статора, уравновешивается основной ЭДС E1, ЭДС рассеяния и падением напряжения на активном сопротивлении обмотки статора:

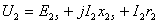

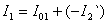
40. Чтобы векторы ЭДС, напряжений и токов обмоток статора и ротора можно было изобразить на одной векторной диаграмме, следует параметры обмотки ротора привести к обмотке статора, т. е. обмотку ротора с числом фаз m2, обмоточным коэффициентом ko62 и числом витков одной фазной обмоткиω2 заменить обмоткой с m1, ω1 и kоб1. При этом мощности и фазовые сдвиги векторов ЭДС и токов ротора после приведения должны остаться такими же, что и до приведения. Пересчет реальных параметров обмотки ротора на приведенные выполняется по формулам, аналогичным формулам приведения параметров вторичной обмотки трансформатора (см. § 1.6).
При s = 1 приведенная ЭДС ротора
где ke = E1/ E2 =ko61 ω1 /(ko62/ ω2) — коэффициент трансформации напряжения в асинхронной машине при неподвижном роторе. Приведенный ток ротора
В отличие от трансформаторов в асинхронных двигателях коэффициенты трансформации напряжения и тока не равны ( kе ≠ ki ). Объясняется это тем, что число фаз в обмотках статора и ротора в общем случае не одинаково ( m1 ≠ m2 ). Лишь в двигателях с фазным ротором, у которых m1 = m2, эти коэффициенты равны.
Активное и индуктивное приведенные сопротивления обмотки ротора:
Следует обратить внимание на некоторую специфику определения числа фаз m2 и числа витков ω2 для короткозамкнутой обмотки ротора (см. рис. 10.3). Каждый стержень этой обмотки рассматривают как одну фазу, а поэтому число витков одной фазы короткозамкнутой обмотки ротора ω2 = ,0,5; обмоточный коэффициент такой обмотки kоб2 = 1, а число фаз m2 = Z2, т. е. равно числу стержней в короткозамкнутой обмотке ротора.
41. В обмотку статора из сети поступает мощность P1. Часть этой мощности идет на потери в стали Pсl, а также потери в обмотке статора Рэ1:
Оставшаяся мощность посредством магнитного потока передается на ротор и называется электромагнитной мощностью:
Часть электромагнитной мощности затрачивается на покрытие электрических потерь в обмотке ротора:
Оставшаяся мощность преобразуется в механическую, получившую название полной механической мощности:
Воспользовавшись ранее полученной формулой
запишем выражение полной механической мощности:
т.е. мощность электрических потерь пропорциональна скольжению.
Мощность на валу двигателя P2 меньше полной механической мощности Р2’ на величину механических Рмех и добавочных Рдоб потерь:
Коэффициент полезного действия есть отношение мощности на валу P2 к потребляемой мощности P1:
42. Электромагнитный момент асинхронной машины создается в результате взаимодействия тока в обмотке ротора с вращающимся магнитным полем. Связь между моментом и скоростью вращения ротора можно получить из уравнения механической мощности. Если в него подставить выражение для тока ротора, то с учетом того, что угловая частота вращения равна 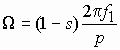
Все величины, входящие в это выражение константы, кроме скольжения s. Взяв производную 


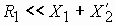


Из выражения для 


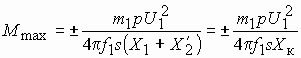
Полагая 




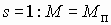
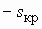
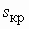
Номинальный режим работы двигателя соответствует скольжению 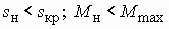

Если за счет внешнего вращающего момента вал двигателя раскручивается до скорости выше синхронной 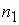
При скольжениях 
На рисунке 


Выражение 

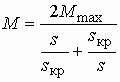



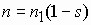


Линеаризованная механическая характеристика рабочего участка примет вид
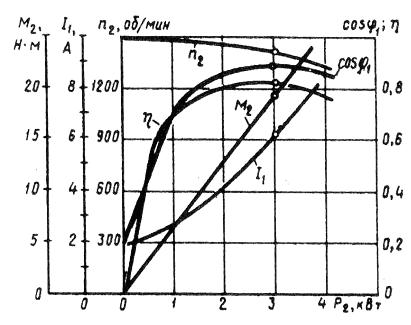
43. Рабочие характеристики асинхронного двигателя представляют собой графически выраженные зависимости частоты вращения n2, КПД η, полезного момента (момента на валу) М2, коэффициента мощности cos φ, и тока статора I1 от полезной мощности Р2 при U1 = const f1 = const.
Скоростная характеристика n2 = f(P2). Частота вращения ротора асинхронного двигателя n2 = n1(1 — s).
Скольжение s = Pэ2/Pэм, т. е. скольжение асинхронного двигателя, а следовательно, и его частота вращения определяются отношением электрических потерь в роторе к электромагнитной мощности. Пренебрегая электрическими потерями в роторе в режиме холостого хода, можно принять Рэ2 = 0, а поэтому s ≈ 0 и n20 ≈ n1.
По мере увеличения нагрузки на валу асинхронного двигателя отношение s = Pэ2/Pэм растет, достигая значений 0,01 — 0,08 при номинальной нагрузке. В соответствии с этим зависимость n2 = f(P2) представляет собой кривую, слабо наклоненную к оси абсцисс. Однако при увеличении активного сопротивления ротора двигателя r2′ угол наклона этой кривой увеличивается. В этом случае изменения частоты асинхронного двигателя n2 при колебаниях нагрузки Р2 возрастают. Объясняется это тем, что с увеличением r2′ возрастают электрические потери в роторе.
Рис. 1. Рабочие характеристики асинхронного двигателя двигателя
Зависимость М2 =f(P2). Зависимость полезного момента на валу асинхронного двигателя М2 от полезной мощности Р2 определяется выражением M2 = Р2/ ω2 = 60 P2/ (2πn2) = 9,55Р2/ n2,
где Р2 — полезная мощность, Вт; ω2 = 2πf 2/ 60 — угловая частота вращения ротора.
Из этого выражения следует, что если n2 = const, то график М2 =f2(Р2) представляет собой прямую линию. Но в асинхронном двигателе с увеличением нагрузки Р2 частота вращения ротора уменьшается, а поэтому полезный момент на валу М2 с увеличением нагрузки возрастает не сколько быстрее нагрузки, а следовательно, график М2 =f (P2) имеет криволинейный вид.
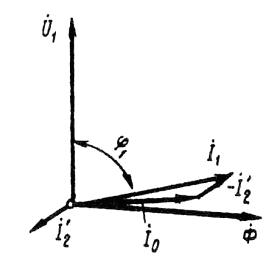
Рис. 2. Векторная диаграмма асинхронного двигателя при небольшой нагрузке
Зависимость cos φ1 = f (P2). В связи с тем что ток статора асинхронного двигателя I1 имеет реактивную (индуктивную) составляющую, необходимую для создания магнитного поля в статоре, коэффициент мощности асинхронных двигателей меньше единицы. Наименьшее значение коэффициента мощности соответствует режиму холостого хода.Объясняется это тем, что ток холостого хода электродвигателя I0 при любой нагрузке остается практически неизменным. Поэтому при малых нагрузках двигателя ток статора невелик и в значительной части является реактивным (I1 ≈ I0). В результате сдвиг по фазе тока статора относительно напряжения получается значительным (φ1 ≈ φ0), лишь немногим меньше 90° (рис. 2).
44. Пусковые свойства асинхронного двигателя зависят от особенностей его конструкции, в частности от устройства ротора.
Пуск асинхронного двигателя сопровождается переходным процессом машины, связанным с переходом ротора из состояния покоя в состояние равномерного вращения, при котором момент двигателя уравновешивает момент сил сопротивления на валу машины.
При пуске асинхронного двигателя имеет место повышенное потребление электрической энергии из питающей сети, затрачиваемое не только на преодоление приложенного к валу тормозного момента и покрытие потерь в самой асинхронном двигателе, но и на сообщение движущимся звеньям производственного агрегата определенной кинетической энергии. Поэтому при пуске асинхронный двигатель должен развить повышенный вращающий момент.
Для асинхронного двигателя с фазным ротором начальный пусковой момент, соответствующий скольжению sп= 1, зависит от активных сопротивлений регулируемых резисторов, введенных в цепь ротора.
Рис. 1. Пуск трехфазного асинхронного двигателя с фазным ротором: а — графики зависимости вращающего момента двигателя с фазным ротором от скольжения при различных активных сопротивлениях резисторов в цепи ротора, б — схема включения резисторов и замыкающих контактов ускорения в цепь ротора.
Так, при замкнутых контактах ускорения У1, У2, т. е. при пуске асинхронного двигателя с замкнутыми накоротко контактными кольцами, начальный пусковой момент Мп1 = (0,5 -1,0) Мном, а начальный пусковой ток Iп = (4,5 — 7) Iном и более.
Малый начальный пусковой момент асинхронного электродвигателя с фазным ротором может оказаться недостаточным для приведения в действие производственного агрегата и последующего его ускорения, а значительный пусковой ток вызовет повышенный нагрев обмоток двигателя, что ограничивает частоту его включений, а в маломощных сетях приводит к нежелательному для работы других приемников временному понижению напряжения. Эти обстоятельства могут явиться причиной, исключающей использование асинхронных двигателей с фазным ротором с большим пусковым током для привода рабочих механизмов.
45. Для пуска асинхронного двигателя с короткозамкнутым ротором применяются следующие способы:
· пуск при пониженном напряжении питания.
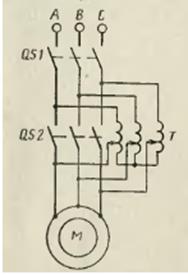
40.2.1. Прямое включение
Прямое включениеасинхронного двигателя в сеть является наиболее простым способом пуска двигателя. В то же время в этом случае обмотки статора и ротора двигателя обтекаются большим пусковым током (током КЗ), равным 4—7-кратному значению номинального. Поэтому очень важно, чтобы время пуска двигателя было при этом как можно меньшим. Такой метод пуска применяется для небольших двигателей, или для двигателей, приводящих во вращение небольшие механические нагрузки.
40.2.2. Пуск при пониженном, напряжении
Пуск при пониженном напряжении питания осуществляется обычно в тех случаях, когда прямой пуск не допускается по условиям работы сети.
Обычно применяют один из четырех способов пуска при пониженном напряжении:
- двигателя через понижающий автотрансформатор;
- переключение обмотки статора со звезды на треугольник;
- включение двигателя через полупроводниковый регулятор напряжения.
Во всех этих случаях снижение напряжения ведет не только к пропорциональному уменьшению пускового тока (положительный эффект), но и к резкому (квадратичному) уменьшению пускового момента (отрицательный эффект).
а) Пуск асинхронного двигателя через автотрасформатор
На рис.40.1. показана схема пуска асинхронного двигателя через автотрансформатор.
Рис.40.1. Пуск асинхронного двигателя с помощью автотрансформатора
Уменьшения напряжения при пуске можно достигать включением между сетью и двигателем понижающего автотрансформатора Т(рис. 40.1). При пуске сначала замыкают рубильник QS1,и пониженное напряжение попадает на обмотки двигателя. По достижении ротором достаточной частоты вращения замыкают рубильник OS2,шунтируя автотрансформатор так, что полное напряжение сети попадает на обмотки двигателя.
б) Пуск с переключением обмоток статора со звезды на треугольник
К способам пуска с понижением напряжения можно отнести также пуск с переключением обмоток статора со звезды на треугольник (рис. 40.2).
Рис.40.2. Схема пуска двигателя с переключением обмоток со звезды на треугольник
В режиме пуска переключатель QSнаходится в положении 

При данном способе пуска фактически снижается напряжение, подводимое к каждой фазе двигателя, поскольку при одинаковом напряжении сети фазное напряжение в схеме звезды в 

46. Частота вращения асинхронного двигателя
Из этого выражения видно, что ее можно регулировать, изменяя частоту f1 питающего напряжения, число пар полюсов р и

скольжение s. Последнее при заданных значениях момента на валу Мвн и частоты f1 можно изменять путем включения в цепь обмотки ротора реостата.
Регулирование путем изменения частоты питающего напряжения.Этот способ требует наличия преобразователя частоты, к которому должен быть подключен асинхронный двигатель. На основе управляемых полупроводниковых вентилей (тиристоров) созданы статические преобразователи частоты и построен ряд опытных электровозов и тепловозов с асинхронными двигателями, частота вращения которых регулируется путем изменения частоты питающего напряжения. Такой способ регулирования частоты вращения ротора асинхронного двигателя является весьма перспективным.
Регулирование путем изменения числа пар полюсов. Этот способ позволяет получить ступенчатое изменение частоты вращения. Для этой цели отдельные катушки 1, 2 и 3, 4, составляющие одну фазу (рис. 266), переключаются так, чтобы изменялось соответствующим образом направление тока в них (например, с последовательного согласного соединения на встречное). При согласном включении катушек (рис. 266, а) число полюсов равно четырем, при встречном включении (рис. 266, б) — двум. Катушки двух других фаз, сдвинутые в пространстве на 120°, соединяются таким же образом. Такое же уменьшение числа полюсов можно осуществить при переключении катушек с последовательного на параллельное соединение. При изменении числа полюсов изменяется частота вращения n1магнитного поля двигателя, а следовательно, и частота вращения n его ротора. Если нужно иметь три или четыре частоты вращения n1, то на статоре располагают еще одну обмотку, при переключении которой можно получить еще две частоты. Существуют двигатели, которые обеспечивают изменение частоты вращения n1 при постоянном наибольшем моменте или при приблизительно постоянной мощности (рис. 267).
В асинхронном двигателе число полюсов ротора должно быть равно числу полюсов статора. В короткозамкнутом роторе это условие выполняется автоматически и при переключении обмотки статора никаких изменений в обмотке ротора выполнять не требуется.



В двигателе же с фазным ротором в этом случае надо было бы изменять число полюсов обмотки ротора, что сильно усложнило бы его конструкцию, поэтому такой способ регулирования частоты вращения используется только в двигателях с коротко-замкнутым ротором. Такие двигатели имеют большие габаритные размеры и массу по сравнению с двигателями общего применения, а следовательно, и большую стоимость. Кроме того, регулирование осуществляется большими ступенями; при частоте f1 = 50 Гц частота вращения поля n1 при переключениях изменяется в отношении 3000:1500:1000:750.
Регулирование путем включения в цепь ротора реостата. При включении в цепь обмотки ротора реостата с различным сопротивлением (Rп4, RпЗ, Rп2 и т. д.) получаем ряд реостатных механических характеристик 4, 3 и 2 двигателя. При этом некоторому нагрузочному моменту Мном (рис. 268) будут соответствовать меньшие частоты вращения n4, n3, n2 и т. д., чем частота nе при работе двигателя на естественной характеристике 1 (при Rп = 0). Это способ регулирования может быть использован только для двигателей с фазным ротором. Он позволяет плавно изменять частоту вращения в широких пределах. Недостатками его являются большие потери энергии в регулировочном реостате, поэтому его используют только при кратковременных режимах работы двигателя (при пуске и пр.).
47. Конденсаторные двигатели — разновидность асинхронных двигателей, в обмотки которого включены конденсаторы для создания сдвига фазы тока.[1] Подключаются в однофазную сеть посредством специальных схем. По количеству фаз статора делятся на двухфазные и трехфазные.
Существует разные схемы подключения, больше вариантов для трёхфазных двигателей, различающиеся способом соединения обмоток двигателя и составом дополнительных элементов, но минимальная работоспособная схема содержит один конденсатор, от чего и происходит название.
Как правило, одна из обмоток («фаза двигателя») запитывается напрямую от однофазной сети, а другие обмотки запитывается через электрический конденсатор, который сдвигает фазу подводимого тока почти на +90°, или через катушку индуктивности, которая сдвигает фазу почти на −90°. Чтобы результирующее вращающееся магнитное поле не было эллиптическим, последовательно с конденсатором включается переменный проволочный резистор, с помощью которого добиваются кругового вращающегося магнитного поля.
Однофа́зный дви́гатель — электродвигатель, конструктивно предназначенный для подключения к однофазной сети переменного тока. Фактически является двухфазным, но вследствие того, что рабочей является только одна обмотка, двигатель называют однофазным.
48. Большинство синхронных машин имеет электромагнитное возбуждение. Источниками постоянного тока для обмоток возбуждения являются специальные системы возбуждения, к которым предъявляется ряд важных требований:
1) надежное и устойчивое регулирование тока возбуждения в любых режимах работы машины;
2) достаточное быстродействие, для чего применяется форсировка возбуждения, т. е. быстрое увеличение напряжения возбуждения до предельного значения, называемого потолочным. Форсировка возбуждения применяется для поддержания устойчивой работы машины во время аварий и в процессе ликвидации их последствий. Потолочное напряжение возбуждения выбирают не менее 1,8-2 номинального напряжения возбуждения. Скорость нарастания напряжения при форсировке возбуждения должна быть не менее 1,5-2 номинальных напряжений на контактных кольцах ротора в секунду;
3) быстрое гашение магнитного поля, т. е. уменьшение тока возбуждения машины до нуля без значительного повышения напряжения на ее обхмотках. Необходимость в гашении поля возникает при отключении генератора или повреждении в нем.
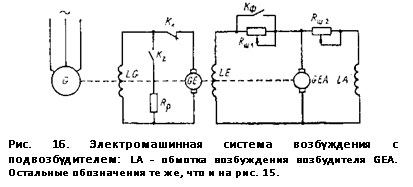
Для возбуждения синхронных машин применяется несколько систем. Простейшей из них является электромашинная система возбуждения с возбудителем постоянного тока (рис. 15). В этой системе в качестве источника используют специальный генератор постоянного тока GE, называемый возбудителем; он приводится во вращение от вала синхронного генератора, а его мощность составляет 1- 3 % мощности синхронного генератора. Ток возбуждения синхронной машины Iв относительно велик и составляет несколько сотен и даже тысяч ампер. Поэтому его регулируют с помощью реостатов, установленных в цепи возбуждения возбудителя. Возбуждение возбудителя осуществляют по схеме самовозбуждения (рис. 15) или независимого возбуждения от специального генератора постоянного тока GEA, называемого подвозбудителем (рис. 16). Подвозбудитель работает с самовозбуждением, и сопротивление резистора Rш2при работе генератора не изменяется.
49. Метод асинхронного пуска. Синхронный двигатель не имеет начального пускового момента. Если его подключить к сети переменного тока, когда ротор неподвижен, а по обмотке возбуждения проходит постоянный ток, то за один период изменения тока, электромагнитный момент будет дважды изменять свое направление, т. е. средний момент за период равняется нулю. При этих условиях двигатель не сможет прийти во вращение, так как его ротор, обладающий определенной инерцией, не может быть в течение одного полупериода разогнан до синхронной частоты вращения. Следовательно, для пуска синхронного двигателя необходимо разогнать его ротор с помощью внешнего момента до частоты вращения, близкой к синхронной.
В настоящее время для этой цели применяют метод асинхронного пуска. При этом методе синхронный двигатель пускают как асинхронный, для чего его снабжают специальной коротко-замкнутой пусковой обмоткой, выполненной по типу «беличья клетка». Чтобы увеличить сопротивление стержней, клетку изготовляют из латуни. При включении трехфазной обмотки статора в сеть образуется вращающееся магнитное поле, которое, взаимодействуя с током Iпв пусковой обмотке (рис. 6.48, а), создает электромагнитные силы F и увлекает за собой ротор. После разгона ротора до частоты вращения, близкой к синхронной, постоянный ток, проходящий по обмотке возбуждения, создает синхронизирующий момент, который втягивает ротор в синхронизм.
Применяют две основные схемы пуска синхронного двигателя. При схеме, изображенной на рис. 6.48, б,обмотку возбуждения сначала замыкают на гасящий резистор, сопротивление которого Rдоб превышает в 8 — 12 раз активное сопротивление Rв обмотки возбуждения. После разгона ротора до частоты вращения, близкой к синхронной (при s ≈ 0,05), обмотку возбуждения отключают от гасящего резистора и подключают к источнику постоянного тока (возбудителю), вследствие чего ротор втягивается в синхронизм. Осуществить пуск двигателя с разомкнутой обмоткой возбуждения нельзя, так как во время разгона ротора при s > 0 в ней вращающимся магнитным полем индуцируется ЭДС Ев = 4,44f2wвФm = 4,4f1swвФm , где f2 = f1s — частота изменения тока в обмотке возбуждения; wв — число витков обмотки возбуждения; Фm — амплитуда магнитного потока вращающегося поля.
В начальный момент пуска при s = 1 из-за большого числа витков обмотки возбуждения ЭДС Ев может достигать весьма большого значения и вызвать пробой изоляции. При схеме, изображенной на рис. 6.48, в, обмотка возбуждения постоянно подключена к возбудителю, сопротивление которого по сравнению с сопротивлением Rв весьма мало, поэтому эту обмотку в режиме асинхронного пуска можно считать замкнутой накоротко. С уменьшением скольжения до
s = 0,3 ÷ 0,4 возбудитель возбуждается и в обмотку возбуждения подается постоянный ток, обеспечивающий при s ≈ 0,05 втягивание ротора в синхронизм. Различие пусковых схем обусловлено тем, что не во всех случаях может быть применена более простая схема с постоянно подключенной к возбудителю обмоткой возбуждения (рис. 6.48, в), так как она имеет худшие пусковые характеристики, чем более сложная схема, приведенная на рис. 6.48,б. Главной причиной ухудшения пусковых характеристик является возникновение одноосного эффекта — влияние тока, индуцируемого в обмотке возбуждения при пуске, на характеристику пускового момента.
50. Под реакцией якоря в синхронных машинах понимают воздействие магнитного поля статора (якоря) на магнитное поле ротора. Реакция якоря оказывает сильное влияние на все электромагнитные процессы в машине. Явление реакции по определению связано с магнитным полем статора, поэтому характер и степень влияния реакции определяется током статора, т.е. нагрузкой машины.
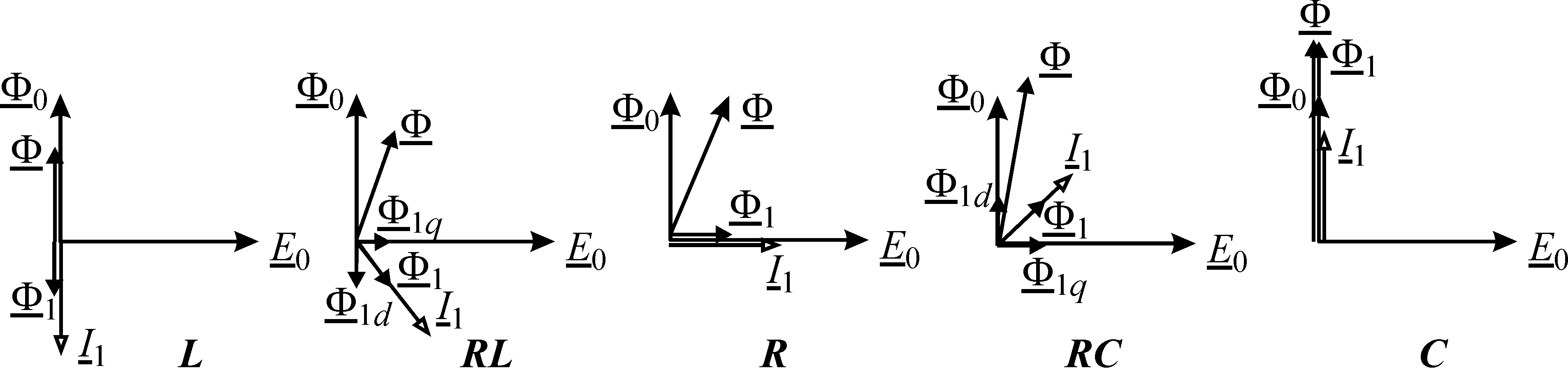



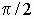
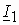



При чисто активной нагрузке (R) ток 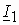




При чисто индуктивной нагрузке (L) ток статора и магнитный поток отстают от ЭДС 
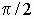


При чисто емкостной нагрузке (C) ток статора и магнитный поток опережают ЭДС на 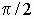
В случае активно-реактивной нагрузки (RL и RC) поток статора оказывается смещенным на угол меньший, чем 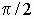



Таким образом реакция якоря в синхронной машине изменяет величину и направление магнитного потока, в отличие от асинхронной машины, у которой 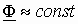
Магнитный поток 


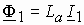

📸 Видео
ЭЛЕКТРОЛИТИЧЕСКАЯ ДИССОЦИАЦИЯ ХИМИЯ 8 класс // Подготовка к ЕГЭ по Химии - INTENSIVСкачать

Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Условия смещения химического равновесия. 9 класс.Скачать

Статика. Момент сил. Условия равновесия тел | Физика ЕГЭ, ЦТ, ЦЭ | Физика для школьниковСкачать

Урок 70. Виды равновесия. Условие равновесия тела при отсутствии вращения.Скачать

Урок 186 (осн). Электрический ток в жидкостях. Закон Фарадея для электролизаСкачать

Асинхронный электропривод. Математические модели. ПоложенияСкачать

Электромеханические переходные процессы. Устойчивость. Уравнение движение ротора.Скачать
Урок 142 (осн). Решение задачСкачать

Модуль №3. Принцип работы асинхронного электродвигателя.Скачать

Принцип работы генератора переменного токаСкачать

Урок 354. Математическое описание процессов в колебательном контуреСкачать

Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Студенты российского вуза разработали вечный двигатель #вечныйдвигатель #изобретенияСкачать

Раскрытие тайн электромагнитной волныСкачать