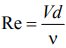Уравнения движения воздуха о рейнольдса

Видео:Урок 138. Число Рейнольдса. Критерий Рейнольдса.Скачать

Калькулятор для расчета Re онлайн

Расчет по общей формуле

Расчет Re для воды

Расчет Re для воздуха

Видео:Потери напора при движении жидкостиСкачать

Формула

Расчетная формула числа Рейнольдса Re в общем виде:

где — плотность среды, кг/м 3 ; — характерная скорость, м/с; — гидравлический диаметр, м; — динамическая вязкость среды, Па·с или кг/(м·с); — кинематическая вязкость среды ( ), м 2 /с; — объёмный расход потока, м 3 /с; — площадь сечения канала, например, трубы, м 2 .

Для труб круглого сечения расчетная формула числа Рейнольдса Re будет:

• V — характерная скорость, м/с;
• d — внутренний диаметр трубы, м;
• — кинематическая вязкость среды ( ), м 2 /с;

Видео:Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Физический смысл

Физический смысл – число Рейнольдса Re характеризует смену режимов течения от ламинарного к турбулентному. Re является критерием подобия течения вязкой жидкости.

Критерий назван в честь выдающегося английского физика Осборна Рейнольдса (1842—1912).

В настоящее время не существует строгого научно доказанного объяснения этому явлению, однако наиболее достоверной гипотезой считается следующая: смена режимов движения жидкости определяется отношением сил инерции к силам вязкости в потоке жидкости. Если преобладают первые, то режим движения турбулентный, если вторые – ламинарный.

Видео:1. Определение числа РейнольдсаСкачать

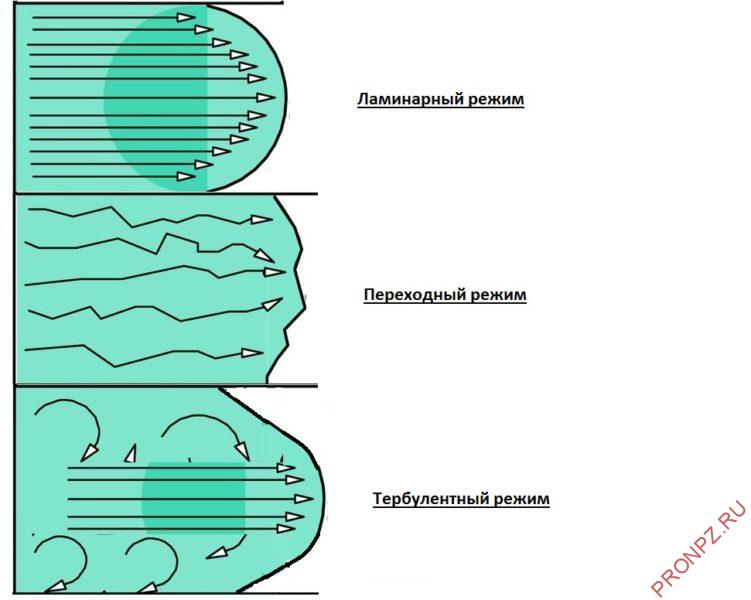
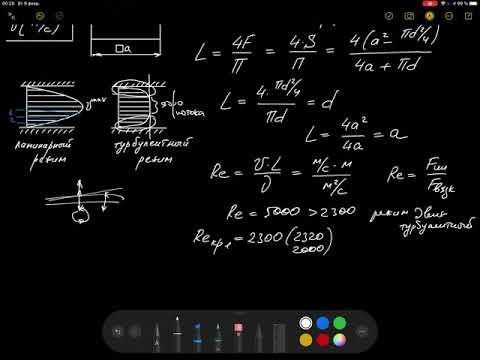
Режимы течения

Режим течения в динамическом пограничном слое зависит от числа Рейнольдса Re и может быть:

1. Ламинарный режим – слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления, все линии тока направлены параллельно.
2. Турбулентный режим – течение, сопровождающееся интенсивным перемешиванием жидкости с пульсациями скоростей и давлений, наряду с основным продольным перемещением жидкости наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости.

Эпюры скоростей

Видео:Вывод уравнений движения идеальной жидкости - Лекция 2Скачать

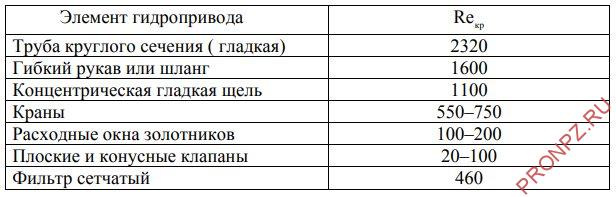
Критическое значение

Переход к турбулентному режиму течения жидкости в пограничном слое определяется критическим значением числа Рейнольдса. Это обусловлено тем, что при возрастании скорости, участвующей в расчете числа Re, его значение растет.
Таким образом, переход от ламинарного режима к турбулентному наблюдается при определенной скорости движения жидкости. Эта скорость называется критической Vкр.

Значение критического числа Re для различных элементов гидропривода

Видео:Закон БернуллиСкачать

Размерность

Числе Re не имеет единиц измерения. Re является безразмерным критерием подобия течения вязкой жидкости.

Видео:Режимы течения жидкости, ламинарный и турбулентный режимыСкачать

Течение в трубе

При ламинарном течении жидкости в прямой трубе или канале постоянного сечения все линии тока направлены параллельно оси трубы, при этом отсутствуют поперечные перемещения частиц жидкости.

При турбулентном течении в канале наряду с основным продольным перемещением жидкости в трубе наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости.

Зависимость режима течения от значения числа Re в гладких трубах:

• 2300 – Турбулентный режим

Обычно предполагается, что при числе Re выше 2300 образуется турбулентный режим.

Тем не менее, при значениях Re выше критического и до определённого предела наблюдается переходной (смешанный) режим течения жидкости, когда турбулентное течение более вероятно, но ламинарное в некоторых конкретных случаях тоже наблюдается — так называемая неустойчивая турбулентность. В трубах такой переходный интервал может достигать вплоть до Re = 2300—10 000.

Видео:Закон БернуллиСкачать

Число Рейнольдса | Это 10+ важных фактов

Видео:Вычислительная гидродинамика (ВГД). Уравнение Рейнольдса и метод конечных объемовСкачать

Content

• Определение числа Рейнольдса
• Уравнение числа Рейнольдса
• Единицы числа Рейнольдса
• Число Рейнольдса для ламинарного потока
• Число Рейнольдса воды
• Число Рейнольдса для турбулентного потока
• Число Рейнольдса в трубе
• Число Рейнольдса воздуха
• Диапазон чисел Рейнольдса
• Таблица чисел Рейнольдса
• Число Рейнольдса кинематическая вязкость
• Цилиндр числа Рейнольдса
• Число Рейнольдса массовый расход
• Число Рейнольдса ламинарное против турбулентного
• Число Рейнольдса для плоской пластины
• Число Рейнольдса в зависимости от коэффициента лобового сопротивления
• Число Рейнольдса сферы
• Что такое число Рейнольдса?
• Значение числа Рейнольдса
• Рейнольдс эксперимент
• Критическое число Рейнольдса

Видео:Определение режима движения жидкости. Число Рейнольдса.Скачать

Определение числа Рейнольдса

«Число Рейнольдса — это отношение сил инерции к силам вязкости».

Число Рейнольдса — это безразмерное число, используемое для изучения жидкостных систем различными способами, такими как структура потока жидкости, природа потока и различные параметры механики жидкости. Число Рейнольдса также важно при изучении теплопередачи. Разработано много взаимосвязей, в том числе число Рейнольда в механике жидкости, трибологии и теплопередаче. Приготовление различных лекарств в аптеке требовало исследования числа Рейнольда.

На самом деле это представление и сравнение силы инерции и силы вязкости.

Видео:Турбулентность на высоких скоростях и число Рейнольдса ( видео 15) | Жидкости | ФизикаСкачать

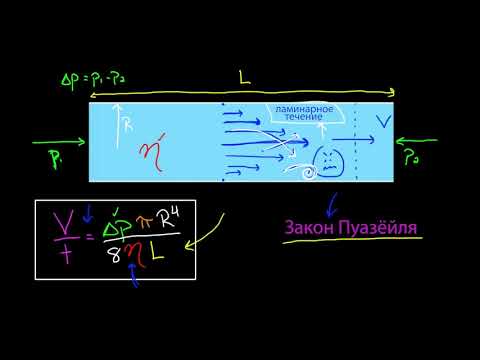
Уравнение числа Рейнольдса

Безразмерное число Рейнольдса показывает, будет ли текущая жидкость ламинарным или турбулентным потоком с учетом некоторых свойств, таких как скорость, длина, вязкость и тип потока. Число Рейнольда обсуждается следующим образом:

Число Рейнольдса обычно называется отношением силы инерции к силе вязкости и характеризует характер потока, такой как ламинарный, турбулентный и т. Д. Давайте посмотрим на уравнение, как показано ниже,

Подставляя выражение силы инерции и силы вязкости в числовое выражение Рейнольдса, мы получаем

В приведенном выше уравнении

Re = число Рейнольдса (безразмерное число)

? = плотность жидкости (кг / м 3 )

V = скорость потока (м / с)

D = Диаметр потока или трубы / Характеристическая длина (м)

μ = вязкость жидкости (Н * с / м 2 )

Видео:Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Единицы числа Рейнольдса

Число Рейнольда безразмерно. Единицы числа Рейнольдса нет.

Видео:Галилео. Эксперимент. Закон БернуллиСкачать

Число Рейнольдса для ламинарного потока

Идентификация потока может быть возможна, зная число Рейнольдса. Число Рейнольдса ламинарного потока меньше 2000. Если в эксперименте вы получите значение числа Рейнольда меньше 2000, то вы можете сказать, что поток является ламинарным.

Видео:Урок 137. Движение тела в жидкости и газе.Скачать

Число Рейнольдса воды

Уравнение числа Рейнольдса имеет вид

Если мы проанализируем приведенное выше уравнение, значение числа Рейнольдса зависит от плотности жидкости, скорости потока, диаметра потока прямо и обратно пропорционально вязкости жидкости. Если жидкостью является вода, то плотность и вязкость воды — параметры, которые напрямую зависят от воды.

Видео:Турбулентное течение круче ламинарного [Veritasium]Скачать

Число Рейнольдса для турбулентного потока

Как правило, эксперимент с числом Рейнольдса может предсказать картину течения. Если значение числа Рейнольдса> 4000, то течение считается турбулентным.

Видео:Движение тел в жидкостях и газах. Лобовое сопротивление и подъемная сила. Формула Стокса. 10 класс.Скачать

Коэффициент сопротивления (Cd) против числа Рейнольдса (Re) в различных объектах

Видео:Теорема Эйлера о движении жидкостиСкачать

Число Рейнольдса в трубе

Если жидкость течет по трубе, мы хотим вычислить число Рейнольдса жидкости, протекающей по трубе. Все остальные параметры зависят от типа жидкости, но за диаметр принимается диаметр трубы Гидравлика D_H (Для этого поток должен правильно выходить из трубы)

Видео:Механика - Движение вязкой жидкости. Эффект МагнусаСкачать

Число Рейнольдса воздуха

Как мы обсуждали в Число Рейнольда для воды, Число Рейнольдса для воздуха напрямую зависит от плотности и вязкости воздуха.

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Диапазон чисел Рейнольдса

Число Рейнольдса — это критерий, по которому можно определить, является ли поток турбулентным или ламинарным.

Если рассматривать поток внутренний, то

Если Re 4000 представляет турбулентный поток

Если значение Re находится между ними (например, от 2000 до 4000), представляет собой переходный поток.

Таблица чисел Рейнольдса

График изменчивости построен между числом Рейнольдса и коэффициентом трения для различной шероховатости.

Мы можем найти коэффициент трения Дарси-Вайсбаха с числом Рейнольдса. Для определения коэффициента трения разработана аналитическая корреляция.

Число Рейнольдса кинематическая вязкость

Кинематическая вязкость определяется как,

Уравнение числа Рейнольдса,

Вышеприведенное уравнение образуется, как показано ниже, если записать его в виде кинематической вязкости,

Цилиндр числа Рейнольдса

Если жидкость протекает через цилиндр, и мы хотим вычислить число Рейнольдса жидкости, протекающей через цилиндр. Все остальные параметры зависят от типа жидкости, но за диаметр принимается диаметр гидравлики D._H (Для этого поток должен правильно выходить из цилиндра)

Число Рейнольдса массовый расход

Затем мы анализируем уравнение числа Рейнольдса, если хотим увидеть взаимосвязь между числом Рейнольдса и массовым расходом.

Как мы знаем из уравнения неразрывности, массовый расход выражается следующим образом:

Помещая значения массового расхода в уравнение для числа Рейнольдса,

Из приведенного выше выражения ясно видно, что число Рейнольдса имеет прямую связь с массовым расходом.

Ламинарное против турбулентного потока число Рейнольдса | Число Рейнольдса ламинарное против турбулентного

Как правило, в механике жидкости мы анализируем два типа потока. Один из них — это ламинарный поток, который происходит с низкой скоростью, а другой — турбулентный поток, который обычно возникает с высокой скоростью. Его название описывает ламинарный поток, поскольку частицы жидкости текут в пластине (линейно) по всему потоку. В турбулентном потоке жидкость движется беспорядочно по всему потоку.

Давайте разберемся в этом важном моменте подробно,

Ламинарный поток

В ламинарном потоке соседние слои жидких частиц не пересекаются друг с другом и текут в параллельных направлениях, что называется ламинарным потоком.

В ламинарном потоке все слои жидкости текут по прямой линии.

• Существует возможность возникновения ламинарного течения, когда жидкость течет с малой скоростью и диаметр трубы небольшой.
• Течение жидкости с числом Рейнольдса меньше 2000 считается ламинарным.
• Течение жидкости очень линейное. Есть пересечение соседних слоев жидкости, и они текут параллельно друг другу и поверхности трубы.
• В ламинарном потоке напряжение сдвига зависит только от вязкости жидкости и не зависит от плотности жидкости.

Турбулентный поток

Турбулентный поток противоположен ламинарному. Здесь, в потоке жидкости, соседние слои текущей жидкости пересекаются друг с другом и не текут параллельно друг другу, что называется турбулентным потоком.

Соседние слои жидкости или частицы жидкости не движутся по прямой в турбулентном потоке. Они беспорядочно текут в зигзагообразных направлениях.

• Турбулентный поток возможен, если скорость текущей жидкости высока, а диаметр трубы больше.
• По значению числа Рейнольдса можно определить турбулентный поток. Если значение числа Рейнольдса больше 4000, то поток считается турбулентным.
• Текущая жидкость не течет в одном направлении. Происходит смешение или пересечение различных слоев жидкости, и они не текут в параллельных направлениях друг к другу, а пересекаются друг с другом.
• Напряжение сдвига зависит от его плотности в турбулентном потоке.

Число Рейнольдса для плоской пластины

Если анализировать обтекание плоской пластины, то число Рейнольдса рассчитывается по характерной длине плоской пластины.

В приведенном выше уравнении диаметр D заменен на L, которая представляет собой характеристическую длину потока по плоской пластине.

Число Рейнольдса в зависимости от коэффициента лобового сопротивления

Предположим, что значение числа Рейнольдса меньше силы инерции. Есть более высокая вязкая сила, которая преобладает над силой инерции.

Если вязкость жидкости выше, то сила сопротивления выше.

Число Рейнольдса сферы

Если вы хотите рассчитать это для этого случая, формула

Здесь диаметр D принимается как гидравлический диаметр сферы в таких расчетах, как цилиндр и труба.

Что такое число Рейнольдса?

Число Рейнольдса — это отношение силы инерции к силе вязкости. Re указывает на это. Это безразмерное число.

Значение числа Рейнольдса | Физическое значение числа Рейнольдса

Число Рейнольда — это не что иное, как сравнение двух сил. Одна — это сила инерции, а вторая — сила вязкости. Если мы возьмем оба соотношения сил, получится безразмерное число, известное как число Рейнольдса. Это число помогает узнать характеристики потока и узнать, какая из двух сил больше влияет на поток. Число Рейнольда также важно для оценки картины течения.

Вязкая сила -> Выше -> Ламинарный поток -> Течение масла

Сила инерции -> Высшее -> Турбулентный поток> Океанские волны

Рейнольдс эксперимент

Осборн Рейнольдс впервые провел эксперимент Рейнольдса в 1883 году и заметил, что движение воды имеет ламинарный или турбулентный характер.

Этот эксперимент очень известен в механике жидкости. Этот эксперимент широко используется для определения и наблюдения трех потоков. В этом эксперименте вода течет через стеклянную или прозрачную трубку.

Краситель впрыскивается потоком воды в стеклянную трубку. Вы можете заметить поток краски внутри стеклянной трубки. Если цвет краски отличается от цвета воды, это хорошо заметно. Если краситель течет линейно или линейно, то поток является ламинарным. Если краситель показывает турбулентность или не течет по прямой, мы можем рассматривать турбулентный поток. Этот эксперимент прост и информативен для студентов, чтобы узнать о потоке и числе Рейнольдса.

Критическое число Рейнольдса

Критическое число Рейнольдса является переходной фазой ламинарного и турбулентного течения. Когда поток меняется с ламинарного на турбулентный, значение числа Рейнольдса считается критическим числом Рейнольдса. Обозначается как Re_Кр. Для каждой геометрии это критическое число Рейнольдса будет другим.

Заключение

Число Рейнольдса является важным термином в области техники и науки. Он используется при изучении потока, теплопередачи, фармацевтики и т. Д. Мы разработали эту тему подробно из-за ее важности. Мы включили в эту тему несколько практических вопросов и ответов.

Число Рейнольдса: для чего оно нужно, как рассчитывается, упражнения

Число Рейнольдса: для чего оно нужно, как рассчитывается, упражнения — Наука

Содержание:

В Число Рейнольдса (р_{а также}) — безразмерная числовая величина, которая устанавливает связь между силами инерции и вязкими силами движущейся жидкости. Силы инерции определяются вторым законом Ньютона и отвечают за максимальное ускорение жидкости. Вязкие силы — это силы, которые препятствуют движению жидкости.

Число Рейнольдса применяется к любому типу потока жидкости, например к потоку в круглых или некруглых каналах, в открытых каналах и потоке вокруг погруженных тел.

Значение числа Рейнольдса зависит от плотности, вязкости, скорости жидкости и размеров пути тока. Поведение жидкости в зависимости от количества энергии, которая рассеивается из-за трения, будет зависеть от того, является ли поток ламинарным, турбулентным или промежуточным. По этой причине необходимо найти способ определения типа потока.

Один из способов определить это — экспериментальные методы, но они требуют большой точности измерений. Другой способ определить тип потока — получить число Рейнольдса.

В 1883 году Осборн Рейнольдс обнаружил, что, если значение этого безразмерного числа известно, можно предсказать тип потока, который характеризует любую ситуацию с проводимостью жидкости.

Для чего нужно число Рейнольдса?

Число Рейнольдса используется для определения поведения жидкости, то есть для определения того, является ли течение жидкости ламинарным или турбулентным. Течение является ламинарным, когда силы вязкости, которые противодействуют движению жидкости, являются доминирующими, и жидкость движется с достаточно малой скоростью и по прямолинейному пути.

Жидкость с ламинарным потоком ведет себя так, как будто это бесконечные слои, которые упорядоченно скользят друг по другу без перемешивания. В круглых воздуховодах ламинарный поток имеет параболический профиль скорости с максимальными значениями в центре воздуховода и минимальными значениями в слоях вблизи поверхности воздуховода. Значение числа Рейнольдса в ламинарном потоке равно р_{а также} 4000.

Переход между ламинарным потоком и турбулентным потоком происходит для значений числа Рейнольдса между 2000 Y 4000.

Как рассчитывается?

Уравнение, используемое для расчета числа Рейнольдса в воздуховоде круглого сечения:

ρ = Плотность жидкости (кг / м 3 )

V = Скорость потока (м 3 / с)

D = Характерный линейный размер пути прохождения жидкости, который в случае круглого воздуховода представляет собой диаметр.

η = динамическая вязкость жидкости (Па · с)

Связь между вязкостью и плотностью определяется как кинематическая вязкость. v = η/ρ, и его единица м 2 / с.

Уравнение числа Рейнольдса как функции кинематической вязкости:

В трубопроводах и каналах с некруглым поперечным сечением характерный размер известен как гидравлический диаметр. D_ЧАС y представляет собой обобщенный размер пути прохождения жидкости.

Обобщенное уравнение для расчета числа Рейнольдса в трубопроводах с некруглым поперечным сечением:

V´ = Средняя скорость потока =Идет

Гидравлический диаметр D_ЧАС устанавливает связь между областью К поперечное сечение потока и смоченный периметр п_M .

Мокрый периметр п_M представляет собой сумму длин стенок трубопровода или канала, контактирующих с жидкостью.

Вы также можете рассчитать число Рейнольдса жидкости, окружающей объект. Например, сфера, погруженная в жидкость, движущуюся со скоростью V. Сфера испытывает силу сопротивления F_р определяется уравнением Стокса.

р = радиус сферы

Число Рейнольдса шара со скоростью V погруженные в жидкость:

р_{а также} 1 при турбулентном потоке.

Решенные упражнения

Ниже приведены три упражнения по применению числа Рейнольдса: Круглый канал, Прямоугольный канал и Сфера, погруженная в жидкость.

Число Рейнольдса в воздуховоде круглого сечения

Рассчитайте число Рейнольдса пропиленгликоля a 20°C в воздуховоде круглого сечения диаметром 0,5 см. Величина скорости потока равна 0,15 м 3 / с. Какой тип потока?

D =0,5 см = 5.10 -3 м (характерный размер)

Плотность жидкости составляет ρ = 1,036 г / см 3 = 1036 кг / м 3

Вязкость жидкости составляет η =0,042 Па · с = 0,042 кг / м.с

Скорость потока V = 0,15 м 3 / с

Уравнение числа Рейнольдса используется для круглого воздуховода.

р_{а также} = (1036 кг / м 3 x0,15 м 3 / с x 5,10 -3 м)/(0,042 кг / м.с) = 18,5

Течение ламинарное, потому что значение числа Рейнольдса мало по отношению к соотношению р_{а также} 3

Динамическая вязкость η = 1,074 мПа · с = 1,074,10 -3 кг / м.с

Сначала определяется средняя скорость потока.

V = 25 мл / мин = 4,16,10 -7 м 3 / с

Поперечное сечение прямоугольное, стороны 0,005 и 0,008 м. Площадь поперечного сечения составляет A = 0,005 м x0,008 м = 4,10 -5 м 2

V´ = (4,16.10 -7 м 3 / с) / (4.10 -5 м 2 )= 1,04×10 -2 РС

Смачиваемый периметр — это сумма сторон прямоугольника.

Гидравлический диаметр D_ЧАС = 4А / П_M

Число Рейнольдса получается из уравнения р_{а также} = ρV´ D_ЧАС/η

р_{а также} = (789 кг / м 3 х1,04 × 10 -2 м / с x1,23.10 -2 м) / 1074,10 -3 кг / м.с

Течение является турбулентным, поскольку число Рейнольдса очень велико (р_{а также}>2000)

Число Рейнольдса для сферы, погруженной в жидкость

Сферическая частица латексного полистирола радиусом р= 2000 нм брошен вертикально в воду с начальной скоростью величинойV₀= 10 м / с. Определите число Рейнольдса частицы, погруженной в воду.

Плотность частицρ=1,04 г / см 3 = 1040 кг / м 3

Число Рейнольдса получается из уравнения р_{а также} = ρV R/η

р_{а также} = (1000 кг / м 3 Икс10 м / с Икс 0,000002 м) / 0,001 кг / (м с)

Число Рейнольдса 20. Течение турбулентное.

Приложения

Число Рейнольдса играет важную роль в механике жидкости и теплопередаче, потому что это один из основных параметров, характеризующих жидкость. Некоторые из его приложений упомянуты ниже.

1-Он используется для моделирования движения организмов, которые перемещаются по жидким поверхностям, таких как: бактерии, взвешенные в воде, которые плавают в жидкости и вызывают беспорядочное движение.

2-Он имеет практическое применение в потоках труб и в каналах циркуляции жидкости, в ограниченных потоках, особенно в пористых средах.

3-В суспензиях твердых частиц, погруженных в жидкость и в эмульсиях.

4-Число Рейнольдса применяется при испытаниях в аэродинамической трубе для изучения аэродинамических свойств различных поверхностей, особенно в случае полетов самолетов.

5-Он используется для моделирования движения насекомых в воздухе.

6-Конструкция химических реакторов требует использования числа Рейнольдса для выбора модели потока с учетом потерь напора, потребления энергии и площади передачи тепла.

7-В прогнозировании теплопередачи электронных компонентов (1).

8-В процессе полива садов и огородов необходимо знать поток воды, выходящей из труб. Чтобы получить эту информацию, определяется гидравлическая потеря напора, которая связана с трением, которое существует между водой и стенками трубы. Потеря напора рассчитывается после получения числа Рейнольдса.

Приложения в биологии

В биологии изучение движения живых организмов в воде или в жидкостях со свойствами, подобными воде, требует получения числа Рейнольдса, которое будет зависеть от размера организмов и скорости, с которой они перемещаются. сместить.

Бактерии и одноклеточные организмы имеют очень низкое число Рейнольдса (р_{а также}1), следовательно, течение имеет ламинарный профиль скорости с преобладанием вязких сил.

Организмы, близкие по размеру к муравьям (до 1 см), имеют число Рейнольдса порядка 1, что соответствует переходному режиму, в котором силы инерции, действующие на организм, столь же важны, как и силы вязкости жидкости.

У более крупных организмов, таких как люди, число Рейнольдса очень велико (р_{а также}1).

Ссылки

1. Применение моделей турбулентного потока с низким числом Рейнольдса для прогнозирования теплопередачи электронных компонентов.Роджерс, П. и Эвелой, В. NV: s.n., 2004, IEEE, Vol. 1, стр. 495-503.
2. Мотт, Р. Л. Прикладная механика жидкости. Беркли, Калифорния: Pearson Prentice Hall, 2006, Vol. I.
3. Коллие, А. М. и Пауни, Д. Дж. Механические и термические свойства материалов. Нью-Йорк: Крейн Руссак, 1973.
4. Кей, Дж. М. и Неддерман, Р. М. Введение в механику жидкости и теплопередачу. Нью-Йорк: Cambridge Universitty Press, 1974.
5. Хаппель Дж. И Бреннер Х. Механика жидкостей и транспортных процессов. Хингем, Массачусетс: Издательство MartinusS Nijhoff, 1983.

Как мотивировать команду на работе: 8 советов

Отказ от курения делает вас толстым? Связь между курением и увеличением веса