Видео:Урок 79. Центр масс тела и методы определения его положенияСкачать
Уравнения движения центра масс самолета
Самолет движется в воздухе по действием аэродинамической силы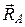 
, силы тяги двигателей 
и силы тяжести 
. С аэродинамической силой и ее проекциями на оси различных систем координат мы познакомились при изучении основ аэродинамики. Сила тяги создается силовой установкой самолета. Вектор обычно располагается в базовой плоскости самолета и образует некоторый угол с осью 0X связанной системы координат, но для простоты мы будем полагать, что этот угол равен нулю, а сам вектор приложен в центре масс.
Полет самолета можно условно разбить на несколько этапов: взлет, набор высоты, горизонтальный полет, снижение и посадка. Самолет также может совершать вираж и другие маневры. На некоторых этапах полета движение самолета может быть как установившимся, так и неустановившимся. При установившемся движении самолет летит с постоянной скоростью, при неизменных углах атаки, крена и скольжения. Ниже мы будем рассматривать только установившееся движение на этапах горизонтального полета, набора высоты и снижения.
Установившийся горизонтальный полет – это прямолинейный полет с постоянной скоростью на постоянной высоте (см. рис. 39). Уравнения движения центра масс самолета запишутся в этом случае следующим образом:
(48)
Поскольку угол атаки a мал (при этом cos a » 1, а sin a » 0), то можно записать:
(49)
Рис. 39. Схема сил, действующих на самолет в установившемся
Если первое из этих равенств не будет выполняться, то скорость самолета будет либо увеличиваться, либо уменьшаться, т.е. не будет выполняться условие установившегося движения. Если же подъемная сила не равна силе тяжести, то самолет будет либо подниматься, либо снижаться, а это значит, что не будет выполняться условие горизонтального полета. Из этого равенства, зная формулу подъемной силы (35), можно получить величину скорости, необходимую для выполнения горизонтального полета Vг.п.
Учитывая, что G = mg (где m – масса самолета, а g – ускорение свободного падения), можно записать:
, (50)
(51)
Из этой формулы видно, что скорость горизонтального полета зависит от массы самолета, плотности воздуха r (которая зависит от высоты полета), площади крыла Sкр и коэффициента подъемной силы Cya. Поскольку Cya напрямую зависит от угла атаки a, то каждому значению скорости горизонтального полета будет соответствовать единственное значение угла атаки. Поэтому для обеспечения установившегося горизонтального полета с требуемой скоростью летчик задает определенную тягу двигателей и величину угла атаки.
Установившийся набор высоты – прямолинейное движение самолета вверх с постоянной скоростью. Схема сил, действующих на самолет при установившемся наборе высоты с углом наклона траектории q, показана на рис. 40.
Рис. 40. Схема сил, действующих на самолет при установившемся
наборе высоты (угол атаки принят малым и не показан)
В этом случае уравнения движения примут вид:
(52)
Необходимо отметить, что при наборе высоты тяга двигателей P уравновешивает не только силу лобового сопротивления Xa, как в горизонтальном полете, но и составляющую силы тяжести Gsinq. Подъемная сила Ya при этом требуется меньшая, поскольку Gcosq
Видео:Движение центра масс твердого телаСкачать
УРАВНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС САМОАЕТА В ПРОЕКЦИЯХ НА ОСИ СВЯЗАННОЙ И ТРАЕКТОРНОЙ СИСТЕМ КООРДИНАТ
Уравнения движения центра масс самолета (1.3) записывают в проекциях на оси выбранной в зависимости от решаемой задачи системы координат. Обычно в качестве таких систем координат выбирают связанную, траекторную и скоростную системы координат. Для упрощения вывода уравнений движения центра масс самолета рассмотрим его полет в спокойной атмосфере без ветра.
Применяя к первому уравнению системы (1.3) формулу дифференцирования вектора скорости материальной точки, движущейся относительно неподвижной системы отсчета, можем переписать это уравнение в виде
где 
— вектор локальных производных
вектора скорости; /, /, к — орты выбранной системы координат;
Ух, Уу, У, — проекции вектора скорости центра масс самолета на оси выбранной системы координат; со — вектор угловой скорости вращения подвижной системы координат, связанной с самолетом, относительно неподвижной системы отсчета; юхК — векторное произведение векторов ® и У.
Рассмотрим уравнения движения центра масс самолета в проекциях на оси связанной и траекторной систем координат [3,5,6].
Уравнения движения центра масс самолета в проекциях на оси свя — занной системы координатОХУХ. Связанная система координат вращается относительно нормальной системы координат с угловой скоростью® = (® О.
Для интегрирования системы дифференциальных уравнений
(1.14) . (1.16) необходимо задать начальные условия Vx(0), К,, (0), Vz (0), X х (0), Я (0), Z? (0), от(0),атакже программы изменения по времени тяги двигателя Р(1), эйлеровых углов у(/), 9(/), у(/) и аэродинамических углов а(/) и Р(0-
Уравнения движения самолета как твердого тела в проекциях на оси связанной системы координат OXYZ. Для того чтобы получить систему уравнений движения самолета как твердого тела (а не материальной точки!), к уравнениям движения центра масс (1.14),
(1.15) и кинематическим уравнениям (1.11), определяющим изменения углов рыскания, тангажа и крена, необходимо добавить систему уравнений вращательного движения самолета вокруг центра масс. Система скалярных уравнений вращательного движения самолета вокруг центра масс получается из второго векторного уравнения (1.3), записанного в проекциях на оси связанной системы координат.
Вычислим производную вектора главного кинетического момента К в предположении, что суммарный кинетический момент роторов ТРД Кр не изменяется по времени:
Подставим в левую часть развернутое выражение для главного кинетического момента, получим
Матрица тензора инерции (У) имеет вид
Кинетический момент роторов двигателей Кр обычно направлен вдоль оси вращения роторов, поэтому
Элементами матрицы тензора инерции являются осевые (I х, Iу, I,) ицентробежные (1ху, IХ1, Iу,) моменты инерции.
Операция 
понимается как умножение матрицы (У) на
вектор 
Выполняя преобразования, получим
где М Л, Му, М г —проекции вектора аэродинамического момента на оси связанной системы координат; МХр, Мур, Мгр — проекции вектора момента тяги двигателя, обусловленного его эксцентриситетом относительно центра масс, на оси связанной системы координат.
Система уравнений (1.18) называется уравнениями моментов и достаточно сложна для анализа движения самолета. Однако в предположении ф,, = 0 и при наличии у самолета плоскости симметрии ОХ? уравнения (1.18) можно существенно упростить, гак как в этом случае /хг = Iп = 0 и уравнения моментов принимают вид 
где 
В случае, когда можно пренебречь слагаемыми с 1ху (режимы малых угловых ускорений и скоростей), система уравнений (1.19) примет наиболее простой вид
Необходимо отметить, что в общем случае уравнения моментов даже в своей наиболее простой форме (1.20) могут быть решены только численными методами при заданных начальных условиях сох(0), со,(0), сог (0).
Уравнение движения центра масс самолета в проекциях на оси гра — екторной системы координат ОХ УКХК. Вектор угловой скорости Ок =(сохк, со^, согк) вращения траекторной системы координат ОХк У к относительно неподвижной системы отсчета вычисляется как результат двух последовательных поворотов траекторной системы координат относительно осей нормальной системы координат на угол пути и угол наклона траектории 0 и записывается в виде
Поскольку ось ОХк траекторной системы координат направлена по вектору земной скорости Ук, проекции Кк на оси этой системы координат имеют вид 
Найдем проекции тяги, аэродинамических сил и веса на оси траекторией системы координат ОХкУк1к.
Проекции тяги вычисляются по формуле
Выполняя преобразования, получим
Проекции аэродинамических сил вычисляются по формуле
Раскрывая матрицы, получим 
Проекции веса вычисляются по формуле 
Раскрывая матрицы, получим 
Подставляя найденные выражения для проекции вектора скоростей и сил на оси траекторной системы координат в (1.13), получим систему дифференциальных уравнений относительно земной скорости VK, угла наклона траектории 0 и угла пути Ч’
Уравнения (1.21) дополняются кинематическими уравнениями, определяющими продольную дальность, высоту полета и боковую дальность самолета в неподвижной системе отсчета,
К уравнениям (1.21), (1.22) необходимо добавить уравнение (1.16), описывающее изменение массы самолета. Интегрирование уравнений (1.20). (1.22) выполняется численными методами при заданных начальных условиях Кк(0), 0(0), ЧЧО), Z?(0), Я(0), Z?(0),/и(0) и заданных программах изменения тяги P(t) и аэродинамических углов a(t), р(/), у Д/).
Уравнения движения центра масс с учетом ветра в проекциях на оси траекторной системы координат ОХк Ук ZK. Все уравнения движения центра масс самолета, рассмотренные выше, были получены в предположении отсутствия ветра. Скорость ветра оказывает существенное влияние на формирование аэродинамических сил и моментов как через изменение воздушной скорости, так и через изменения аэродинамических углов атаки « и скольжения (1 Рассмотрим учет скорости ветра в уравнениях движения самолета.
Скорость ветра У/ определяется в проекциях на оси нормальной системы координат ОХ%:
Вектор воздушной скорости V выражается через вектор земной скорости Кк и вектор скорости ветра ?:
Выражения для проекции вектора воздушной скорости на оси нормальной системы координат имеют вид
Для определения аэродинамических углов атаки а и скольжения (3 необходимо знать проекции вектора воздушной скорости на оси связанной системы координат ОХУ2
Теперь углы атаки и скольжения с учетом ветра могут быть вычислены по формулам 
Зная углы атаки и скольжения, можно пересчитать аэродинамические силы, заданные в скоростной системе координатору,^, в проекции на оси связанной системы координат ОХУХ. Складывая их с проекциями тяги, получим проекции сил (кроме проекций веса) на оси связанной системы координат:
Выполняя последний переход от связанной системы координат ОХУХ к траекторией ОХ к УКХ к искладывая полученный результат с проекциями веса, получим проекции всех сил на оси траекторной системы координат с учетом скорости ветра:
Подставляя выражения для проекций сил в правые части уравнений (1.21), получим систему дифференциальных уравнений относительно земной скорости Кк, угла наклона траектории 0 и угла пути Ч’ с учетом скорости ветра
В этих уравнениях элементы матрицы направляющих косинусов /4С С ” и аэродинамические силы должны вычисляться на углах атаки и скольжения и воздушной скорости с учетом ветра по формулам, приведенным выше.
Уравнение движения центра масс в проекциях на оси скоростной системы координат ОХ„УаИ„. Вектор угловой скорости О„ = = (ши,ш уа, сого ) вращения скоростной системы координат относительно неподвижной системы отсчета является суммой угловой скорости вращения самолета как твердого тела со = (со*, со*, со,) и угловой скорости вращения скоростной системы координат 0ХаУа2а относительно связанной системы координатор»>^:
При отсутствии ветра ось ОХа скоростной системы координат направлена по вектору земной скорости Ук. Поэтому V = Ук и выражение для проекций вектора скорости V на оси скоростной системы координат имеет вид
Проекции вектора тяги Р на оси скоростной системы координат имеют вид
или 
Проекции вектора аэродинамических сил на оси скоростной системы координат определяются наиболее просто:
Проекции веса на оси скоростной системы координат выражаются через проекции веса на оси нормальной системы координат:
Подставляя найденные проекции векторов скоростей и сил на оси скоростной системы координат в (1.14) , получим систему дифференциальных уравнений относительно Ук и аэродинамических углов а,р
К уравнениям (1.25) необходимо добавить кинематические уравнения, определяющие положение (дальность, высоту и боковую дальность) центра масс самолета в неподвижной системе отсчета,
Раскрывая это выражение, получим
К уравнениям (1.25), (1.26) необходимо также добавить уравнение изменения массы самолета. Интегрирование уравнений выполняется численными методами при заданных начальных условиях Ук (0), «(0), Р(0), 2(г(0), // (0), Z,, (0), т (0), программах изменения тяги P(t), углов тангажа б(/), крена у(t) и рыскания V|/(f).
Видео:Центр тяжести. СамолетСкачать
УРАВНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА. МАСС САМОЛЕТА
Уравнение движения центра масс в векторной форме
Положение и движение самолета в полете определяют относительно поверхности Земли. Поэтому за основную систему отсчета, принимают геоцентрическую неинерциальную систему координат, связанную с Землей и совершающую вместе с ней суточное
вращение с угловой скоростью со3 (земная система отсчета).
Движение центра масс самолета описывается динамическим
уравнением (1.7), которое после подстановки FBIi = RA + mgr примет вид
m^^P + RA + mgr + F’ + F*, (1.32)
где 1/к — вектор скорости движения центра масс самолета относи-
тельно Земли и gr — вектор гравитационного ускорения.
Переносную и кориолисову силы инерции, связанные с вращением Земли, определяют известными из теоретической механики выражениями
Fe — — mWe == — m[iо3 х (со3 X r)]
KK = — m#K = — 2m(to3 x VK), . (1.33)
где r —- радиус-вектор, проведенный из начала геоцентрической системы отсчета 0° в центр масс самолета; We и И7К — переносное и кориолисово ускорения центра масс, обусловленные вращением выбранной геоцентрической системы отсчета относительно инерциальной. ‘ . .
Поскольку в справочных таблицах обычно приводятся значения ускорения свободного падения с учетом переносной силы инерции в зависимости от высоты, то в правой части уравнения (1.32) можно
геометрическую сумму сил гравитационного притяжеция. mgr и переносной силы инерции F1 заменить силой тяжести G:
G = mgt + Fe — mg. (1-34)
В (1.34) g—вектор результирующего ускорения свободного падения и центробежной силы,.
Векторное уравнение (1,32) с учетом (1.34) запишем в виде
Как было указано в § 1.1, при практическом применении векторное уравнение движения проектируется на оси прямоугольной системы координат. Выбор систёмы координат для составления-дифференциальных уравнений движения центра масс самолета определяется задачей исследования. При исследовании траекторий обычно применяют траекторные оси. В то же время задачи устойчивости и управляемости удобнее рассматривать в связанной системе координат.
Уравнения движения центра масс в траекторией системе координат
Наиболее простую и удобную форму система динамических уравнений движения центра масс самолета (поступательного движения) примет, если векторное уравнение (1.35) спроектировать на оси траекторной системы координат.
Применяя формулы (1.9) для проектирования левой части уравнения (1.35) и учитывая, что 1/*„ = VI:, Vm = Vzi: =0, получим
Ь Р*к‘> тыг^Ук — Р!,к г Уi; b G,;K — F(1.36) — тыугУК — РZK “Ь
где (оун, согк — проекции на траекторные оси вектора угловой ско-
рости (о„ вращения траекторной системы координат относительно Земли; в правой части приведены проекции соответствующих сил на траекторные оси.
Для написания этих уравнений в развернутом виде необходимо
найти проекции угловой скорости сок, а также проекции кориоли-
совой силы инерции FK на траекторные оси. Проекции внешних сил и тяги на эти оси были определены в § 1.6.
Угловую скорость со„ можно представить в виде суммы переносной
угловой скорости сокр нормальной системы 0XgYgZg в системе от-
счета O^X^YqZq и угловой скорости сок& вращения скоростной системы относительно нормальной:
сон = соКр -|- coKg. (1.37)
Переносная угловая скорость сокр, в свою очередь, может быть представлена суммой угловых скоростей:
где К — угловая скорость поворота меридиональной плоскости,
содержащей центр масс О, вокруг оси вращения Земли; ф — угловая скорость поворота радиуса-вектора центра масс в меридиональной плоскости вокруг оси, лежащей в плоскости экватора (см. рис. 1.4).
Угловая скорость coKg также может быть представлена в виде
 |
суммы угловой скорости Фг вокруг ОСИ OYg и угловой скорости 0 вокруг оси OZg (см. рис. 1.5):
Используя табл. I (см. приложение) направляющих косинусов, находим проекции вектора сок на оси OY„ и OZK траекторной системы
co^j, = Я (sin ер cos 0 — cos ф sin Y sin 0) ф sin Y sin 0 + !F cos 0;
согк = Я, cos ф sin V — ф cos V
которые после подстановки выражений (1.21) в результате несложных преобразований будут иметь вид
gj,(K = ¥ cos 0 V sin 4r cos20 tg ф/(/?з — f Я);
co2K = 0 — И cos Q/(R3 + Я). (1.41)
Найдем теперь проекции кориолисовой силы инерции на траек — торные оси. Вектор кориолисовой силы инерции определяется известной из механики формулой
— mwK = — 2т(и3 х Кк) (1-42)
и перпендикулярен (03 и Ук.
Проекции кориолисовой силы инерции на оси траекторной системы выражаются формулами
Кк = 0; FyK = 2ma>aVR cos ф cos
F*к = 2mcoaVK (sin ф cos 0 — cos ф sin ‘P sin 0).
Подставляя в (1.36) выражения для проекций угловых скоростей, определенные формулами (1.41), проекции тяги, аэродинамической силы, силы тяжести (см. формулы (1.27) и (1.28), а также (1.30)) и проекции кориолисовой силы инерции, выраженные формулами (1.43), получим систему динамических уравнений движения центра масс самолета относительно сферической вращающейся Земли в проекциях на оси траекторной системы координат (при отсутствии ветра ук = V, ¥ = фи):
mV — Р cos (а + ф,) cos р — Ха — mg sin 0; (1.44)
— Zu sin y„ — mg cos 0 — j0$mu>3V cos ф sin ‘P — f mV^cos 0/(/?3 Я);
— mV cos 0 *P = P [sin (а + Ф/ ) sin ya — cos (a ф^ зіп p cos yj -|-
-j — Ya sin yu + Za cos ya -1- 2/ж.>зV (sin ф cos 0 — cos ф cos lP sin 0) —
— mV2 cos2 0 sin Y tg ф/(/?8 + Я). (1.46)
Эти уравнения называют уравнениями поступательного движения.
Приведем некоторые оценки величин членов правых частей уравнений (1.44) … (1.46), связанных с суточным вращением Земли и кривизной ее поверхности. Кориолисова сила, связанная с вращением Земли, пропорциональна скорости полета. При скоростях полета свыше 2000 … 3000 м/с кориолисово ускорение составит 2 … 3 % от ускорения свободного падения. Центростремительное
ускорение, обусловленное кривизной Земли, пропорционально квадрату скорости полета и при скорости 1000 м/с достигает около 1,6 % от ускорения свободного падения. При расчете траекторий самолетов, летающих со скоростями до 1000 м/с, кориолисову силу инерции и силу инерции, связанную с кривизной поверхности Земли, обычно не учитывают.
В динамические уравнения движения центра масс входит масса самолета, заметно меняющаяся у некоторых типов самолетов в процессе полета. Э общем случае характер изменения массы самолета из-за выгорания топлива зависит от скорости, высоты полета и режима работы двигателя:
Перегрузка. Уравнения движения центра масс в безразмерной форме
При исследовании многих задач динамики полета используется понятие перегрузки. Перегрузкой называется отношение суммы векторов тяги и полной аэродинамической силы к величине силы тяжести
• —^ . P + RA . ■mg » title=»УРАВНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА. МАСС САМОЛЕТА» align=»left» width=»58″ height=»45 src=»http://ooobskspetsavia.ru/2015/11/06/uravneniya-dvizheniya-centra-mass-samoleta/style=»margin-left:-70px; margin-right:70px»/>
(1.48)
. Вектор перегрузки характеризует маневренность самолета, поскольку он учитывает величину и направление сил, изменяя которые, можно управлять полетом.
Проектируя вектор перегрузки на оси координат, получим составляющие перегрузки по осям. Проекции перегрузки на оси скоростной системы координат равны:
^ cos ( sin(a 4-фр) +FJ; ‘ (1.49)
«;« = -^[—Р COS (a — f фя) sin р + ZJ
и называются соответственно тангенциальной, нормальной’скоростной и боковой перегрузками.
Проекции вектора перегрузки на оси траекторной системы координат составят (при отсутствии ветра):
пхк = і cos (« + Фи)cos Р — *a] = пха
п1т = Р fsln (« + COS Уа + cos (о — f Фя) Stalin уа1 +
В (1.49) и (1.50) аэродинамические силы определены в скоростной системе осей координат. .
‘ Разделив левые и правые части уравнений (1.44) … (1.46) на О = mg, получим динамические уравнения движения центра масс в перегрузках
-jr ё = tlya COS Yu — «za Sin Yu — COS 0 |-
f — cos ф sin ¥ (/?з + //)’. (1.51)
——— — і = nya sin Yu — «70 cos Ya H — — C0B к (simp cos 0 —
— cos ф cos ¥ sin 0) — Vі cosE0 sin ¥ tg
‘При рассмотрении частных случаев движения самолета выражения для проекций перегрузки значительно упрощаются.
Для]) полета без скольжения (ft == О, Za = 0) с малыми углами атаки, когда можно принять sin (a + фР) « а + фР, cos (os + + Фр) » 1, формулы (1.49) и (1.50) примут вид
Р-Ха. .. Р(а + Фр) + Ко. ха
и, без ветра, » ‘ 1 ‘ ■
«зса» пу* =.■«№COS Yu’.. «Лі = «j/аSin Yu — (15 )
В проекциях на связанные оси вектор перегрузки может быть представлен составляющими пх, пу и nz, которые называются продольной, нормальной и поперечной перегрузкой соответственно. Используя таблицу направляющих косинусов, получим
Пх = пха COS a COS Р + пиа sin о — nzu cos os Sin Р; 4
пу — — пха sin a cos Р -)- пуа cos a + пга sin a sin P; (1-54) «г = nxa Si» P + «га cos P-
§ 1.8. ДИНАМИЧЕСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ САМОЛЕТА ОТНОСИТЕЛЬНО ЦЕНТРА МАСС
Исследование движения самолета относительно центра масс (вращательного,- илн углового) удобно выполнять, если использовать динамические уравнения в проекциях на оси связанной системы координат 0XYZ. При изучении углового движения само-
лета так же, как и при определении траекторий центра масс, применяют в качестве системы отсчета неинерциальную систему, связанную с Землей.
Проектируя векторное уравнение (1.8) на оси связанной системы координат и применяя формулы (1.9) для вычисления проекций производных по времени от вектора кинетического момента самолета, получим систему скалярных уравнений движения самолета относительно центра масс (вращательного, или углового движения)
-j — агКх ьзхКг = Мру’, (1.55)
-rff — •+ ЫхКу — Ь)1/Кх = Мрг,
где К. х, К у, Кг — проекции вектора кинетического момента самолета на связанные оси координат; (ох, ыу, (oz — проекции вектора угловой скорости самолета относительно Земли на те же оси; MRx, MRu, MRz — проекции результирующего момента аэродинамических сил и тяги относительно центра масс на те же оси. Следует иметь в виду, что момент массовых сил (сил тяжести, центробежных и кориолисовых сил инерции) вокруг центра масс самолета равен нулю.
Угловая скорость самолета относительно Земли является суммой векторов угловой скорости самолета относительно нормальной
системы координат и угловой скорости (о«р вращения нормальной системы координат относительно Земли вследствие кривизны поверхности Земли, Для реальных условий полета самолета последняя
составляющая ы„р мала и ею можно пренебречь.
Проекции кинетического момента К на произвольные подвижньЙ! оси записываются в теоретической механике^как /’V-;
Кх JХ^Х ‘ /xytoy /хг(0г)
где /ж, Jy, Jz осевые, а 7*„, Jxz, uJyZ — центробежные моменты инерции, которые определяются формулами:
Jx = J (уг + z[5]) dm Jy — J (Xі — f z-) dm)
Jz = j (Xі + Уъ) dm; Jay = jxy dm
Jxi = j xz dm) Jyz = j t/z dm.
Моменты инерции самолетов с заметно изменяющейся в полете массой являются функциями времени.
Поскольку основная плоскость OXY связанной системы координат является плоскостью симметрии самолета, то в связанных осях центробежные моменты инерции, содержащие координаты г, равны нулю: Jxz — Juz — — 0.
С учетом этого упрощения, используя выражения (1.56), уравнения (1.55), запишем в виде
Jх^х ^ху®у і г ^ у) ^ ху^х^у == рх)
Jу®У ^ху®х (/ж ‘ *^г) ®жВ)г Jx^z == ^Ry’i
Jг Ь (^у ^х) ^[>х^[)у Jxy (Щ* Wp) = Аі рг.
Подробнее выражения для проекций результирующего момента MRx, MRy и MRz будут рассмотрены во второй части книги при анализе углового движения самолета.
💥 Видео
СУПЕРДЖЕТ - Анатомия региональника | система управления. Часть 4.Скачать
Аварийная посадка «Летающего танка»СУ25(Грач)без шассиСкачать
Навигация самолета, ILS, АРК, ИНС - Основы авиации #7Скачать
Аэродинамика для всеx - Часть 3 Центровка, Органы управленияСкачать
Первый самолёт в МиреСкачать
Основная Система управления легкого самолетаСкачать
Конструктивно-силовая схема самолета - Основы авиации #11Скачать
Урок 7. Механическое движение. Основные определения кинематики.Скачать
Главные приборы в самолете - Основы авиации #6Скачать
Подъёмная сила крыла ● 1Скачать
Центр давления профиля крылаСкачать
05, Определение координаты движущегося телаСкачать
Центровка авиамоделиСкачать
Расчёт и построение аэродинамических профилей на примере профиля N.A.C.A.Скачать
TFTAERO x Алексей Кочемасов. Про системы самолета Boeing 737 NG. E3Скачать
Система координат. Система отсчетаСкачать
TFTAERO x Алексей Кочемасов. Про системы самолета Boeing 737 NG. Топливная система. E2Скачать
