Видео:Движение центра масс твердого телаСкачать
Уравнения движения центра масс самолета
Самолет движется в воздухе по действием аэродинамической силы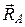 
, силы тяги двигателей 
и силы тяжести 
. С аэродинамической силой и ее проекциями на оси различных систем координат мы познакомились при изучении основ аэродинамики. Сила тяги создается силовой установкой самолета. Вектор обычно располагается в базовой плоскости самолета и образует некоторый угол с осью 0X связанной системы координат, но для простоты мы будем полагать, что этот угол равен нулю, а сам вектор приложен в центре масс.
Полет самолета можно условно разбить на несколько этапов: взлет, набор высоты, горизонтальный полет, снижение и посадка. Самолет также может совершать вираж и другие маневры. На некоторых этапах полета движение самолета может быть как установившимся, так и неустановившимся. При установившемся движении самолет летит с постоянной скоростью, при неизменных углах атаки, крена и скольжения. Ниже мы будем рассматривать только установившееся движение на этапах горизонтального полета, набора высоты и снижения.
Установившийся горизонтальный полет – это прямолинейный полет с постоянной скоростью на постоянной высоте (см. рис. 39). Уравнения движения центра масс самолета запишутся в этом случае следующим образом:
(48)
Поскольку угол атаки a мал (при этом cos a » 1, а sin a » 0), то можно записать:
(49)
Рис. 39. Схема сил, действующих на самолет в установившемся
Если первое из этих равенств не будет выполняться, то скорость самолета будет либо увеличиваться, либо уменьшаться, т.е. не будет выполняться условие установившегося движения. Если же подъемная сила не равна силе тяжести, то самолет будет либо подниматься, либо снижаться, а это значит, что не будет выполняться условие горизонтального полета. Из этого равенства, зная формулу подъемной силы (35), можно получить величину скорости, необходимую для выполнения горизонтального полета Vг.п.
Учитывая, что G = mg (где m – масса самолета, а g – ускорение свободного падения), можно записать:
, (50)
(51)
Из этой формулы видно, что скорость горизонтального полета зависит от массы самолета, плотности воздуха r (которая зависит от высоты полета), площади крыла Sкр и коэффициента подъемной силы Cya. Поскольку Cya напрямую зависит от угла атаки a, то каждому значению скорости горизонтального полета будет соответствовать единственное значение угла атаки. Поэтому для обеспечения установившегося горизонтального полета с требуемой скоростью летчик задает определенную тягу двигателей и величину угла атаки.
Установившийся набор высоты – прямолинейное движение самолета вверх с постоянной скоростью. Схема сил, действующих на самолет при установившемся наборе высоты с углом наклона траектории q, показана на рис. 40.
Рис. 40. Схема сил, действующих на самолет при установившемся
наборе высоты (угол атаки принят малым и не показан)
В этом случае уравнения движения примут вид:
(52)
Необходимо отметить, что при наборе высоты тяга двигателей P уравновешивает не только силу лобового сопротивления Xa, как в горизонтальном полете, но и составляющую силы тяжести Gsinq. Подъемная сила Ya при этом требуется меньшая, поскольку Gcosq
Видео:3.3. Центр масс и закон его движения | Динамика | Александр Чирцов | ЛекториумСкачать
ПОЛНАЯ СИСТЕМА УРАВНЕНИЙ ДВИЖЕНИЯ САМОЛЕТА
В случае анализа динамики самолета, совершающего полет со скоростью, значительно меньшей орбитальной, уравнения движения по сравнению с общшм случаем полета летательного аппарата [13] могут быть упрощены, в частности, можно пренебречь вращением и сферичностью Земли. Кроме этого сделаем еще ряд упрощающих допущений.
Будем считать, что самолет представляет собой абсолютно жесткое тело. Влияние упругости конструкции будем учитывать
только квазистатически, для текущего значения скоростного напора.
Будем считать, что масса и моменты инерции самолета на рассматриваемых интервалах времени неизменны и соответствуют исходному состоянию равновесного полета.
Будем считать, что конфигурация самолета имеет плоскость симметрии и что массы распределены симметрично по отношению к этой плоскости.
При анализе устойчивости и управляемости самолета будем использовать следующие прямоугольные правые системы осей координат.
Нормальная земная система координат OXgYgZg. Эта система осей координат имеет неизменную ориентацию относительно Земли. Начало координат совпадает с центром масс (ЦМ) самолета. Оси 0Xg и 0Zg лежат в горизонтальной плоскости. Их ориентация может быть принята произвольно, в зависимости от целей решаемой задачи. При решении навигационных задач ось 0Xg часто направляют к Северу параллельно касательной к меридиану, а ось 0Zg направляют на Восток. Для анализа устойчивости и управляемости самолета удобно принять направление ориентации оси 0Xg совпадающим по направлению с проекцией вектора скорости на горизонтальную плоскость в начальный момент времени исследования движения. Во всех случаях ось 0Yg направлена вверх по местной вертикали, а ось 0Zg лежит в горизонтальной плоскости и образует вместе с осями OXg и 0Yg правую систему осей координат (рис. 1.1). Плоскость XgOYg называют местной вертикальной плоскостью.
Связанная система координат OXYZ. Начало координат расположено в центре масс самолета. Ось ОХ лежит в плоскости симметрии и направлена вдоль линии хорд крыла (либо параллельно какому-либо другому, фиксированному относительно самолета направлению) к носовой части самолета. Ось 0Y лежит в плоскости симметрии самолета и направлена вверх (при горизонтальном полете), ось 0Z дополняет систему до правой.
Углом атаки а называется угол между продольной осью самолета и проекцией воздушной скорости на плоскость OXY. Угол положителен, если проекция воздушной скорости самолета на ось 0Y отрицательна.
Углом скольжения р называется угол между воздушной скоростью самолета и плоскостью OXY связанной системы координат. Угол положителен, если проекция воздушной скорости на поперечную ось положительна.
Положение связанной системы осей координат OXYZ относительно нормальной земной системы координат OXeYgZg может быть полностью определено тремя углами: ф, #, у, называемыми углами. Эйлера. Последовательно поворачивая связанную систему
Рис. 1.L Нормальная земная OXgYgZg и связанная OXYZ системы координат Рис, 1.2, Углы Эйлера, используемые при исследовании динамики самолетов
координат на каждый из углов Эйлера, можно прийти к любому угловому положению связанной системы относительно осей нормальной системы координат.
При исследовании динамики самолетов используются следующие понятия углов Эйлера.
Угол рыскания г]) — угол между некоторым исходным направлением (например, осью 0Xg нормальной системы координат) и проекцией связанной оси самолета на горизонтальную плоскость. Угол положителен, если ось ОХ совмещается с проекцией продольной оси на горизонтальную плоскость поворотом вокруг оси OYg по часовой стрелке.
Угол тангажа # — угол между продольно# осью самолета ОХ и местной горизонтальной плоскостью OXgZg, Угол положителен, если продольная ось находится выше горизонта.
Угол крена у — угол между местной вертикальной плоскостью, проходящей через ось ОХ у и связанной осью 0Y самолета. Угол положителен, если ось О К самолета совмещается с местной вертикальной плоскостью поворотом вокруг оси ОХ по часовой стрелке. Углы Эйлера могут быть получены последовательными поворотами связанных осей относительно нормальных осей. Будем считать, что нормальная и связанная системы координат в начале совмещены. Первый поворот системы связанных осей произведем относительно оси О на угол рыскания г]; (ф совпадает с осью OYgXрис. 1.2)); второй поворот —относительно оси 0ZX на угол Ф (‘& совпадает с осью OZJ и, наконец, третий поворот произведем относительно оси ОХ на угол у (у совпадает с осью ОХ). Проектируя векторы ф, Ф, у, являющиеся составляющими
вектора угловой скорости движения самолета относительно нормальной системы координат, на связанные оси, получим уравнения связи между углами Эйлера и угловыми скоростями вращения связанных осей:
со2 = ф cos у — ф cos Ф sin у.
При выводе уравнений движения центра масс самолета необходимо рассматривать векторное уравнение изменения количества движения
где ю — вектор скорости вращения связанных с самолетом осей;
R — главный вектор внешних сил, в общем случае аэродинами-
ческих сил и тяги; G — вектор гравитационных сил.
Из уравнения (1.2) получим систему уравнений движения ЦМ самолета в проекциях на связанные оси:
°ixVz) = Ry + G!!’ (1 -3)
т iy’dt “Ь У — = Rz + Gz>
где Vx, Vy, Vz — проекции скорости V; Rx, Rz — проекции
результирующих сил (аэродинамических сил и тяги); Gxi Gyy Gz — проекции силы тяжести на связанные оси.
Проекции силы тяжести на связанные оси определяются с использованием направляющих косинусов (табл. 1.1) и имеют вид:
Gy = — G cos ft cos у; (1.4)
GZ = G cos d sin y.
При полете в атмосфере, неподвижной относительно Земли, проекции скорости полета связаны с углами атаки и скольжения и величиной скорости (V) соотношениями
Vх = V cos a cos р;
Vу = — V sin a cos р;
Видео:Урок 79. Центр масс тела и методы определения его положенияСкачать
Оптимизация конструктивных параметров летательных аппаратов
Оптимизация конструктивных параметров летательных аппаратов
Дифференциальные уравнения движения летательных аппаратов (ЛА), будем называть математической моделью движения ЛА.
Если за признак классификации взять постоянство массы ЛА в полёте, то можно говорить о математических моделях движения ЛА постоянной и переменной массы.
К основным теоремам, используемым при составлении уравнений движения ЛА, относятся теоремы об изменении количества движения, изменении кинетического момента, изменении кинетической энергии. Распространение перечисленных классических теорем на динамику ракет, принадлежащих к классу тел переменного состава (массы), проводятся на основе так называемого принципа затвердевания, формулируемого следующим образом: уравнение движения тела переменного состава можно представлять в форме уравнений движения тела постоянного состава, имеющую мгновенно зафиксированную (затвердевшую) массу. В число сил, действующих на тело в рассматриваемый конкретный момент, включаются внешние силы, реактивные силы Кориолиса и вариационные силы [1, 2,5].
Характер движения оперенного летательного аппарата (ОЛА) вокруг центра масс существенно зависит от способа стабилизации его в полете. В настоящее время широко применяются два способа стабилизации летательных аппаратов (ЛА): вращением и оперением [2, 3].
К причинам, вызывающим колебания неуправляемых ЛА относительно центра масс, относятся следующие основные баллистические факторы.
1. Эксцентриситет силы тяги (МΔ) относительно центра массы ЛА, создается благодаря тому, что вектор силы тяги не совпадает с центром массы ЛА (рис. 2).
2. Начальные возмущения в момент пуска, к которым относят: первоначальный толчок, состоит в получении ЛА начальной угловой скорости вращения (
) относительно экваториальной оси; начальный угол (
) отклонения продольной оси ЛА от направления вектора скорости в момент пуска.
3. Аэродинамическая асимметрия ЛА (перекос, деформация и несимметричность формы элементов стабилизатора и т. п.), которая приводит к появлению дополнительных аэродинамических моментов, вызывающих колебания ЛА относительно центра масс (рис. 1).
Следует отметить, что эксцентриситет силы тяги и центра масс, а также аэродинамическая асимметрия прежде всего обусловлены производственными и эксплуатационными причинами.
Для изучения влияния перечисленных факторов на кучность использована система дифференциальных уравнений (СДУ) движения неоперенного летательного аппарата (НЛА) в возмущенной среде.
Получение математических моделей, описывающих состояние ЛА, имеет своей целью, как правило, определение искомых параметров движения: компонентов скорости движения центра масс, угловой скорости ЛА относительно его центра масс, углов, характеризующих ориентацию аппарата, и, наконец, координат центра масс, по которым может быть построена траектория движения ЛА. В качестве независимой переменной (главного аргумента) в математической модели движения ЛА выступает текущее время t. Основу математической модели, характеризующей состояние ЛА, составляют дифференциальные уравнения движения. Для того чтобы получить их решения в конечной форме, должны быть однозначно заданы начальные условия и определены силы, находящиеся в правых частях дифференциальных уравнений. При этом несущественно, в какой форме задаются воздействия (детерминированный или стохастический подход), важно, чтобы принятая модель сил характеризовалась полной информацией об их значениях в рассматриваемом интервале времени. Именно эта полная совокупность сил, определяющая вид входных воздействий, и будет характеризовать при помощи фазовых координат состояние ЛА в данный и последующий моменты времени [1, 5]
Дифференциальные уравнения пространственного движения получены проектированием на оси полускоростной и полусвязанной систем координат (рис 1, 2) [3, 4] общих векторных уравнений, выражающих содержание теорем о производных по времени от векторов количества и момента количества движения:
(1)
В качестве составляющих главного вектора действующих сил 
были учтены такие силы: сила лобового сопротивления; подъемная сила; сила тяги; сила Кориолиса, возникающая за счет истечения пороховых газов; силы, вызванные эксцентриситетом тяги и центра масс; силы, вызванные вращением Земли.
Составляющими главного момента 
количества движения учитывались следующие моменты: опрокидывающий (для ОЛА – стабилизирующий) момент; экваториальный демпфирующий момент; момент трения; момент Кориолиса, возникающий за счет истечения пороховых газов; моменты, вызванные эксцентриситетом тяги и масс; моменты, вызванные вращением Земли.
Уравнения вращательного движения неоперенного летательного аппарата около его центра масс являются динамическими уравнениями Эйлера, для которых существует наиболее простое представление в проекциях на полусвязанные оси С
(рис. 2) [3, 4].
1. Уравнения движения ЛА при наличии перекоса и смещения с оси симметрии вектора силы тяги
При исследовании этого вопроса будем иметь в виду то, что ЛА все же является телом вращения, причем его ось симметрии одновременно является и осью динамической симметрии. В рассматриваемом случае к ЛА будут приложены следующие дополнительные силы и моменты:
— вследствие смещения и перекоса вектор силы тяги раскладывается на две составляющие, одна из которых параллельна оси симметрии, а вторая – ей перпендикулярна. Вследствие малости угла наклона вектора силы тяги к оси симметрии составляющую, параллельную этой оси, можно принять равной силе тяги;
— вследствие эксцентриситета силы тяги в плоскости сξη (рис.2) возникает отклоняющий реактивный момент МΔ, величина которого равна произведению силы тяги Р на эксцентриситет Δ, стремящийся вращать ЛА относительно центра масс.
Учтем также момент от косо поставленного оперения, который направлен вдоль оси симметрии ЛА и описывается соотношением:
(2)
где 
– угол наклона оперения, L – длинна ЛА, 
– площадь поперечного сечения ЛА, 
–массовая плотность воздуха, V – скорость ЛА, 
– аэродинамический коэффициент, А – полярный момент инерции.
С учетом дополнительных сил и моментов, создаваемых перекосом и смещением с оси симметрии вектора силы тяги, уравнения будут иметь вид [4]:
(3)
где 
.
Рассмотрим, каким же образом влияют конструктивные параметры ЛА на величину характеристик рассеивания по дальности 
и по направлению 
.
Расчет характеристик рассеивания с учетом конструктивных параметров ЛА можно провести по зависимостям [5]:
(4)
.
Поправочные коэффициенты по дальности:
на изменение 
– угла бросания, 
– начальной скорости, 
– баллистического коэффициента, 
, 
– углов нутации, 
, 
– угловых скоростей нутации, 
– линейного эксцентриситета силы тяги, 
– углового эксцентриситета силы тяги, 
– угла наклона сопел, 
, 
– линейных эксцентриситетов центра масс, 
– угловых эксцентриситетов центра масс, 
– угловой скорости собственного вращения ЛА, 
– времени выключения реактивного двигателя, – угла наклона оперения, 
– диаметра оперения, 
– углов нутации в точке выключения двигателя, 
– угловых скоростей нутации в точке выключения двигателя, 
– времени работы реактивного двигателя, 
– дальность полёта ЛА. Коэффициенты, характеризующие разброс соответствующего параметра (фактора): 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, , 
, 
, 
, , 
, 
, 
, 
. Поправочные коэффициенты по дальности рассчитаны с помощью СДУ(7).
Проведенные расчеты с помощью зависимостей (4, 8) показали, что для получения оптимальных характеристик рассеивания по дальности и по направлению , а также для обеспечения устойчивого полета ОЛА, эксцентриситет силы тяги не должен превышать ∆ 
мм, угловой аэродинамический эксцентриситет 
(рис. 4, 7).
2. Влияние асимметрии масс на полет летательных аппаратов
Рассмотрим случай, когда центр масс не лежит на геометрической оси симметрии ЛА, которая, в свою очередь, уже не является главной центральной осью инерции. Будем считать, что вектор силы тяги лежит на геометрической оси симметрии, а центр масс смещен с нее на некоторую величину ε (рис. 1). Данное смещение называется эксцентриситетом силы тяжести. Все оси координат связываем с центром инерции, а положение главных центральных осей Сξ1,η1,
1 относительно связанных осей 
определяем с помощью малых углов γ1 и γ2 (рис. 2).
Учитывая изложенное выше и данные работы [5] получим уравнения вращательного движения с учётом асиметрии центра масс в следующем виде:
Система уравнений (5) отличается от системы (3) наличием в правой части колеблющихся слагаемых, обусловленных асимметрией масс. Заметим также, что в результате асимметрии в правой части первого уравнения системы (5) появляется почти постоянный подкручивающий момент, обусловленный силой тяги 
, поэтому даже невращающийся ОЛА при наличии асимметрии получает с течением времени угловую скорость собственного вращения.
При наличии разного рода асимметрии, особенно если система попадает в «резонансный» режим, существенно изменяется правая часть уравнения, описывающего изменения скорости полета. Последнее означает, что движение ОЛА будет происходить не по расчетной траектории, и в результате кучность ухудшится.
Расчеты, проведенные по зависимостям (4), (8) для ЛА: «Град», «Ураган» для различных дальностей полёта и различных тормозных колец (без тормозного кольца, с большим тормозным кольцом и малым тормозным кольцом), показали, что для получения оптимальных характеристик рассеивания линейный эксцентриситет центра масс не должен превышать 
; угловой 
(рис 5, 8).
3. Влияние силы и момента Кориолиса за счет истечения газов из сопла
Сила и момент Кориолиса возникают в результате движения пороховых газов по камере и соплу (при наличии угловой скорости вращения ЛА, которую обозначим Ω) (рис. 3).
Элементарная сила Кориолиса 
определится по зависимости:
(6)
где dm = ρ∙σ; ρ – плотность газов, σ – свободная от пороха площадь сечения, U – относительная скорость истечения газов.
С учётом размеров пороховой шашки получим силу 
и момент Кориолиса 
за счёт истечения газов [4]:
где 
, 
; 
массовый расход газов через сопло; 
эффективная скорость истечения газов; 
– расстояния, указанные на рис. 3.
Сравнительная оценка показала, что влияние силы Кориолиса невелико и ею можно пренебречь, а момент силы Кориолиса можно сравнить с экваториальным демпфирующим моментом и его необходимо учитывать [4].
Учитывая уравнения 3, 5, 6 и данные работы [4], система дифференциальных уравнений пространственного движения НЛА будет иметь вид:
1. 
2. 
3. 
4. 
5.
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
В данной СДУ описано движение тела (ЛА) переменной массы в которых учтены: силы лобового сопротивления, подъемная сила, сила тяги, сила Кориолиса за счёт истечения пороховых газов, силы, вызванные эксцентриситетом тяги и центра масс, силы, вызванные вращением Земли, опрокидывающий (для ОЛА – стабилизирующий) момент, экваториальный демпфирующий момент, момент трения, момент Кориолиса за счёт истечения пороховых газов, моменты, вызванные эксцентриситетом тяги и центра масс, моменты, вызванные вращением Земли. Все применяемые обозначения введены в работах [2, 3, 5]
Система дифференциальных уравнений была решена при помощи численного интегрирования методом Рунге-Кутта четвертого порядка.
 |
Экспериментальные характеристики рассеивания 
, 
взяты по данным работ [6, 7].
4. Пути улучшения кучности оперенных летательных аппаратов
Проведенные расчеты показывают, что на угловое отклонение (рассеивание) траектории неуправляемых оперенных летательных аппаратов (ОЛА), которое характеризуется углом ψk отклонения вектора скорости в конце активного участка траектории, доминирующее влияние оказывает эксцентриситет силы тяги.
Из результатов видно, что сравнительно медленное вращение оперенных неуправляемых ОЛА вокруг продольной оси приводят к резкому уменьшению влияния эксцентриситета силы тяги и асимметрии центра масс.
Расчеты, проведенные с помощью зависимостей (4) и СДУ (8) показали, что вследствие вращения рассеивание оперенных неуправляемых ЛА по направлению уменьшается в 2–2,5 раза, по дальности – в 1–1,5 раза (рис. 6,9). Таким образом, вращение оперенных неуправляемых ЛА является эффективным средством уменьшения рассеивания и значительно улучшает кучность. Для каждого оперенного неуправляемого ЛА существует некоторая оптимальная угловая скорость вращения r0, при которой рассеивание ЛА принимает оптимальное значения. Проведенные расчеты показали, что оптимальная скорость вращения при сходе с направляющей и в полете которое будет обеспечивать минимальное техническое рассеивание, составляет: для ОЛА: М21ОФ «Град» r0=20,9 рад/с; для 9М55Ф «Смерч», r0=25,1 рад/с; для 9М27Ф «Ураган» r0=22,5 рад/с (рис. 6,9).
Угол наклона оперения для обеспечения оптимальной скорости вращения r0 и устойчивого полета ЛА должен составлять для ОЛА: М21ОФ «Град» αoper=0,049 рад, для 9М27Ф «Ураган» αoper=0,054 рад, для 9М55Ф «Смерч» αoper≤0,087 рад (рис 6.9)
Вращение оперенных направляемых ЛА можно получить одним из сделующих трех способов:
1. за счет реактивного момента, создаваемого наклоном сопел ;
2. за счет придания вращательного движения в момент старта за счет винтовых направляющих;
3. за счет косопоставленного оперения.
1. Выбранная в качестве объекта исследования совокупность типов неуправляемых ЛА позволяет всесторонне изучить особенности динамики их полета и разработать рекомендации по баллистической подготовке как существующих, так и перспективных ЛА.
2. Принятая в работе математическая модель динамики полета ЛА позволяет наиболее полно исследовать особенности баллистики ЛА и определить направления её совершенствования.
3. С целью повышения достоверности результатов исследования особенностей динамики полета ЛА по современной методике, учитывающей как волновое сопротивление, так и сопротивление трения, определены коэффициенты аэродинамических сил и моментов, действующих на ЛА в полете, а также рассчитаны их инерционно-массовые характеристики [4].
4. Вопросы влияния линейного и аэродинамического эксцентриситета силы тяги и асимметрии центра масс, рассмотренные в статье, а также начальные возмущения при сходе ЛА с направляющей и в точке выключения двигателя [4] являются определяющими при расчете оптимальных характеристик рассеивания ЛА.
5. Предложенная система дифференциальных уравнений (7) позволяет выбрать оптимальные конструктивные параметры неуправляемых ЛА, обеспечивающие максимальную дальность полета и минимальное техническое рассеивание.
6. Разработанная программа решения системы дифференциальных уравнений позволяет:
а) проводить вычисления значений параметров движения ЛА с заданным по времени шагом, а также их отклонения относительно невозмущенного движения как в пределах полной траектории, так и по участкам: активном участке траектории, пассивном участке траектории;
б) исследовать поведение ЛА под действием любой совокупности возмущений;
в) производить вычисления по возмущениям, заданным как в конечном виде, так и различными законами распределения.
7. Предложенная математическая модель (4, 7) может быть использована при разработке перспективных летательных аппаратов с различными способами стабилизации.
Часть результатов, представленных в данной работе, была получена при поддержке президента Украины в рамках гранта Государственного фонда фундаментальных исследований.
1. Джамая механіка. – К.: Видавництво «Дрохва», 2004. – 415с.
2. , Лысенко баллистика. – М.: Издательство «Машиностроение», 2005. – 607 с.
3. , и др. Баллистика ствольных систем. Справочная библиотека разработчика-исследователя. – М.: Издательство «Машиностроение», 2006. – 461 с.
4. и др. Математическая модель пространственного движения ЛА на твердом топливе в атмосфере. Вестник СумГУ №2, 2008, с 1-6.
5. О движении тела, содержащего подвижную внутреннюю массу // Доклады АН. 2005, т. 405.
6. Таблицы полета М21ОФ ТС, – 74. М.: – 1975г. – 96с.
7. Таблицы полета 9М27Ф ТС, – 84РГ. М.: – 1988г. – 272с.
8. Черноусько и оптимизация движения тела, управляемого посредством подвижной внутренней массы // Прикладная математика и механика. 2006, т. 70, вып. 6. С. 915-941.
МАКЕЕВ Василий Ильич, кандидат технических наук, доцент, доцент кафедры военной подготовки Сумского государственного университета.
, доктор технических, профессор, старший научный сотрудник Института проблем машиностроения им. Подгорного НАН Украины.
Адрес: г. Харьков, ул.
БОНДАРЬ Александр Вячеславович кандидат технических наук, доцент кафедры компьютерных наук Сумского государственного университета.
Адрес: 40000, /5, кв. 16
ТРОФИМЕНКО Павел Евгеньевич, кандидат военных наук, профессор, профессор кафедры военной подготовки Сумского государственного университета.
Рис. 1 – Положение центра масс при асимметрии.
С0 – несмещённое положение центра масс ЛА; С – смещённое положение центра масс ЛА; ε1, ε – линейное значение эксцентриситета центра масс.
1
 |
 |
 |
Рис. 2 – Положение новых главных центральных осей инерции ЛА при наличии эксцентриситетов центра его масс.
 |
Рис. 3 – Параметры истечения пороховых газов через сопло. Се – центр выходного сечения сопла;
С – центр тяжести.
 |
Рисунок 4 – Зависимость характеристик рассеивания ВD, Вb, BD opt,
Bb opt от дальности полёта, и эксцентриситета силы тяги для ЛА «Град» М21ОФ (без тормозного кольца)
 |
Рисунок 5 – Зависимость характеристик рассеивания ВD, Вb, BD opt,
Bb opt от дальности полёта, и эксцентриситета центра масс для ЛА «Град» М21ОФ
(с малым тормозным кольцом)
 |
Рисунок 6 – Зависимость характеристик рассеивания ВD, Вb, BD opt,
Bb opt от дальности полёта, угловой скорости вращения ЛА и угла наклона оперения для ЛА «Град» М21ОФ
(с большим тормозным кольцом)
Рисунок 7 – Зависимость характеристик рассеивания ВD, Вb, BD opt,
Bb opt от дальности полёта, и эксцентриситета силы тяги для ЛА «Ураган» 9М27Ф (без тормозного кольца)
 |
Рисунок 8 – Зависимость характеристик рассеивания ВD, Вb, BD opt,
Bb opt от дальности полёта, и эксцентриситета центра масс для ЛА «Ураган» 9М27Ф
(с малым тормозным кольцом)
Рисунок 9 – Зависимость характеристик рассеивания ВD, Вb, BD opt,
Bb opt от дальности полёта, угловой скорости вращения ЛА и угла наклона оперения для ЛА «Ураган» 9М27Ф
🔥 Видео
Уравнение Мещерского, формула ЦиолковскогоСкачать
Центр массСкачать
Лемак С. С. - Механика управляемых систем - Двухуровневое управление летательного аппаратаСкачать
Галилео. Эксперимент. Центр массСкачать
Система материальных точек. Центр масс. Закон движения центра масс. Видеоурок по физике 10 классСкачать
Урок 80. Определение положения центра масс телаСкачать
Модель плоского движения для БПЛА с PID управлением на SimInTechСкачать
Урок 106. Реактивное движениеСкачать
АУПО. Силы и моменты, действующие на летательный аппарат. Математическая модель.Скачать
Урок 93. Основное уравнение динамики вращательного движенияСкачать
Основы теории движения космического аппарата. Гр. 1. Часть 1Скачать
ЦЕНТР ТЯЖЕСТИ И ЦЕНТР МАСССкачать
Аэродинамика для всеx - Часть 3 Центровка, Органы управленияСкачать
Урок 7. Механическое движение. Основные определения кинематики.Скачать
Основы теории движения космического аппарата. Гр. 2. Часть 1Скачать
Лемак С. С. - Механика управляемых систем - Лекция 6Скачать
ОЛИМПИАДНАЯ ФИЗИКА. Центр масс системы. Вебинар №15Скачать
