Уравнения движения точки на ободе колеса катящегося без проскальзывания

Видео:Движение колеса без проскальзывания, качение | Олимпиадная физика, кинематика | 9 – 11 классСкачать

Уравнения движения точки на ободе колеса катящегося без проскальзывания

2017-05-07
Точка А находится на ободе колеса радиуса $R = 0,50 м$, которое катится без скольжения по горизонтальной поверхности со скоростью $v = 1,00 м/с$ Найти:
а) модуль и направление вектора ускорения точки А;
б) полный путь $s$, проходимый точкой А между двумя последовательными моментами ее касания поверхности.

Плоское движение твердого тела можно представить как комбинацию смещения центра масс и вращение вокруг центра масс.

$vec_$ — положение вектора A относительно C. В задаче $v_ = v = const$ и вращение без скольжения, т.е. $v_ = v = omega R$, таким образом, $w_ = 0$ и $beta = 0$. Используя эти условия в уравнении (2)

Здесь $hat_$ — единичный вектор, направленный вдоль $vec_$.

(б) Пусть центр колеса движется вправо (положительная ось x), тогда на жесткой горизонтальной поверхности колесо должно вращаться в направлении по часовой стрелке. Если $omega$ угловая скорость колеса, то $omega = frac<v_> = frac$.

Пусть точка A касается горизонтальной поверхности при $t = 0$, далее определим точку A в точке $t = t$,

Следовательно, расстояние, на которое покрывается точка A при $T = 2 pi / omega$

Видео:Качение колеса без проскальзывания. Лекция 2-3Скачать

Уравнения движения точки на ободе колеса катящегося без проскальзывания

Видео:Мгновенный центр вращенияСкачать

§ 83. Качение без проскальзывания

Итак, у нас есть два типа простейшего движения – поступательное и вращательное. До сих пор мы рассматривали их только по отдельности, но теперь я собираюсь познакомить вас с достаточно большим классом задач, где эти движения тесным образом связаны друг с другом.

Вообразите себе автомобильное колесо, движущееся по сухой асфальтированной дороге.

Что интересно, если взять какой-то произвольный момент времени, окажется, что точка, находящаяся в самом низу колеса, покоится. Ее скорость будет равна нулю.

Если у этой точки будет какая-либо скорость, это означает, что колесо будет проскальзывать и не сможет катиться вперед. Но если сцепление с дорогой будет хорошее, точки, находящиеся на кромке колеса, будут поочередно сменять друг друга, тем самым обеспечивая дальнейшее продвижение объекта.

В физике ситуацию, когда тело, вращаясь, обеспечивает свое движение вперед, называют качением без проскальзывания. Именно для такого случая и существует связь между вращательным и поступательным движением.

В чем же заключается эта связь? Давайте представим, что, прежде чем заставить колесо катиться, мы одну из половин испачкали краской, которая при движении частично будет оставаться на дороге.

Допустим, мы позволили колесу пройти расстояние d , соответствующее дуге l (длине его “загрязненной” стороны).

Это расстояние d также показывает, насколько сместился центр масс.

Таким образом, путь который проделает середина колеса совпадает с длиной дуги l :

Эту самую дугу мы можем заменить произведением модуля углового перемещения и радиуса колеса (если возникли вопросы, смотрите § 72):

Мы можем разделить обе части этого уравнения на время движения. Равенство сохранится:

С левой стороны у нас получилась скорость, с которой перемещался центр масс, а с правой – произведение угловой скорости колеса и его радиуса:

Вы можете сказать: «Мы ведь и раньше знали об этой формуле. К чему весь этот сложный ход рассуждений?»

Раньше мы имели дело с формулой, которая связывала линейную скорость какой-либо точки, вращающейся вокруг некоторой оси, с ее угловой скоростью. А сейчас мы получили выражение, связывающее угловую скорость вращающегося объекта с линейной скоростью его центра масс.

Эта формула работает только в том случае, когда тело катится по какой-либо поверхности. Мы рассмотрим с вами задачу на применение этого уравнения в следующем параграфе.

Видео:Траектория точки обода колесаСкачать

Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях – решение задачи

Видео:Никанорова Е. А. - Механика. Семинары - Кинематика материальной точки и простейших системСкачать

Основные законы и формулы, применяемые при решении задач

Вращательное движение вокруг неподвижной оси

Рассмотри твердое тело, вращающееся вокруг неподвижной оси z . Сделаем рисунок. Ось вращения направим перпендикулярно плоскости рисунка, на нас. Пусть φ – угол поворота тела вокруг оси, отсчитываемый от некоторого начального положения. За положительное направление выберем направление против часовой стрелки. Угловая скорость ω равна производной угла поворота по времени t :
.
При , тело вращается против часовой стрелки; при – по часовой. Вектор угловой скорости направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Угловое ускорение ε равно производной угловой скорости по времени:
.
Вектор углового ускорения также направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

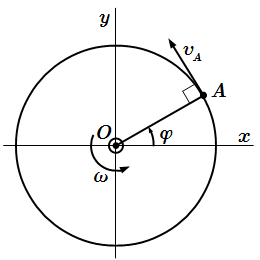
Скорость точки при вращательном движении тела вокруг неподвижной оси

Рассмотрим точку A , принадлежащую твердому телу. Опустим из нее перпендикуляр OA на ось вращения. Пусть – расстояние от точки до оси. Траекторией движения точки A является окружность (или дуга) с центром в точке O радиуса .

Абсолютное значение скорости точки A определяется по формуле:
.
Вектор скорости направлен по касательной к траектории (окружности), перпендикулярно отрезку OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор угловой скорости .

Касательное (или тангенциальное) ускорение точки A определяется аналогично скорости:
.
Оно направлено по касательной к окружности, перпендикулярно OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор углового ускорения .

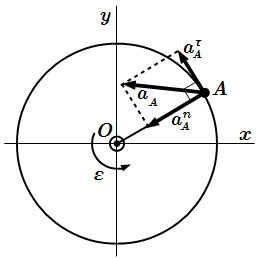
Ускорение точки при вращательном движении тела вокруг неподвижной оси

Нормальное ускорение всегда направлено к центру окружности и имеет абсолютную величину
.

Полное ускорение точки A , или просто ускорение, равно векторной сумме касательного и нормального ускорений:
.
Поскольку векторы и перпендикулярны, то абсолютная величина ускорения точки A определяется по формуле:
.

Поступательное прямолинейное движение

Теперь рассмотрим прямолинейное поступательное движение тела. Направим ось x вдоль его линии движения. Пусть s есть перемещение тела вдоль этой оси относительно некоторого начального положения. Тогда скорость движения всех точек тела равна производной перемещения по времени:
.
При , вектор скорости направлен вдоль оси x . При – противоположно этой оси.

Ускорение точек тела равно производной скорости по времени, или второй производной перемещения по времени:
.
При , вектор ускорения направлен вдоль оси x . При – противоположно.

Соприкосновение тел без проскальзывания

Рассмотрим два тела, находящиеся в зацеплении без проскальзывания. Пусть точка A принадлежит первому телу, а точка B – второму. И пусть, в рассматриваемый момент времени, положения этих точек совпадают. Тогда, если между телами нет проскальзывания, то скорости этих точек равны:
.
Если каждое из тел вращается вокруг неподвижной оси, то равны соответствующие касательные ускорения:
.
Если одно из тел движется поступательно (пусть это второе тело), то ускорение его точек равно касательному ускорению точки соприкосновения первого тела:
.

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Пример решения задачи

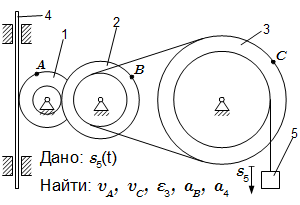
Механизм состоит из ступенчатых колес 1, 2, 3, находящихся в зацеплении и связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 – r₁ = 2 см, R₁ = 4 см, у колеса 2 – r₂ = 6 см, R₂ = 8 см, у колеса 3 – r₃ = 12 см, R₃ = 16 см. На ободьях колес расположены точки A, B и C. Задан закон движения груза: s₅ = t 3 – 6t (см). Положительное направление для s₅ – вниз.

Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.

Указания. Эта задача – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что проскальзывание в ременной передаче и в точках сцепления колес отсутствует. То есть скорости точек колес, находящихся в зацеплении равны, а скорости точек ремня равны скорости точек, лежащих на ободе колес, связанных ременной передачей.

Дано:
t = 2 с; r₁ = 2 см, R₁ = 4 см; r₂ = 6 см, R₂ = 8 см; r₃ = 12 см, R₃ = 16 см; s₅ = t 3 – 6t (см).

Определение скорости и ускорения груза 5

Груз 5 совершает поступательное движение. Поэтому скорости (и ускорения) всех его точек равны. В условии задачи задано смещение s груза относительно некоторого начального положения. Дифференцируя по времени t , находим зависимость скорости точек груза от времени:
.
Дифференцируя скорость груза по времени, находим зависимость ускорения груза от времени:
.

Находим скорость и ускорение груза в заданный момент времени :
см/с;
см/с 2 .

Определение угловых скоростей и ускорений колес

Груз 5 связан нитью с внутренним ободом колеса 3. Поэтому скорости точек внутреннего обода колеса 3 равны скорости груза:
.
Отсюда находим угловую скорость колеса 3 для произвольного момента времени:
.
Здесь подразумевается, что и являются функциями от времени t . Дифференцируя по t , находим угловое ускорение колеса 3:
.
Находим значения угловой скорости и углового ускорения в момент времени с. Для этого подставляем найденные значения и при с:
с –1 ;
с –2 .

Рассмотрим колесо 2. Его внутренний обод связан нитью с внешним ободом колеса 3. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 2 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Рассмотрим колесо 1. Его внутренний обод находится в зацеплении с внешним ободом колеса 2. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 1 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Итак, мы нашли:
ω ₁ = 5.3333 с –1 , ω ₂ = 1.3333 с –1 , ω ₃ = 0.5 с –1 , ε ₁ = 10.6667 с –2 , ε ₂ = 2.6667 с –2 , ε ₃ = 1 с –2 .

Определение скоростей точек A и C

Точка A лежит на окружности радиуса R₁ с центром в точке O₁, расположенной на оси вращения. Поэтому скорость этой точки направлена по касательной к окружности и по абсолютной величине равна
см/с.

Точка C лежит на окружности радиуса R₃ с центром O₃ на оси вращения. Скорость этой точки:
см/с.

Определение ускорения точки B

Точка B лежит на окружности радиуса R₂ с центром O₂, расположенном на оси вращения. Касательное (или тангенциальное) ускорение этой точки направлено по касательной к окружности в сторону, на которую указывает угловое ускорение (по часовой стрелке). По абсолютной величине оно равно
см/с 2 .

Нормальное ускорение всегда направлено к центру окружности. По абсолютной величине оно равно
см/с 2 .

Полное ускорение равно векторной сумме касательного и нормального ускорений:
.
Поскольку касательное ускорение перпендикулярно нормальному, то для абсолютной величины полного ускорения имеем:
см/с 2 .

Определение ускорения рейки 4

Рейка 4 движется поступательно по направляющим. Она находится в зацеплении с внешним ободом колеса 1. Поэтому ее скорость равна скорости точек внешнего обода колеса 1:
.
Дифференцирую по времени, получаем ускорение рейки в произвольный момент времени:
.
Подставляем численные значения для момента времени t = 2 с :
см/с 2 .

см/с; см/с; с –2 ; см/с 2 ; см/с 2 .

Автор: Олег Одинцов . Опубликовано: 25-10-2019

💥 Видео

Качение без проскальзыванияСкачать

Вращательное движение. 10 класс.Скачать

колесо катится с ускорениемСкачать

Мгновенная ось вращения. Лекция 2-2Скачать

Урок 101. Скатывание тела с наклонной плоскостиСкачать

Скатывание тела (колеса, цилиндра) по наклонной плоскостиСкачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Кинематика точкиСкачать

Дифференциальные уравнения движения точкиСкачать

Кинематика точки Движение по окружностиСкачать

Поступательное и вращательное движенияСкачать

Разбор Относительность механического движения, задача 2Скачать

Разбор задач по механикеСкачать

Общая физика | Лекция 2: Кинематика. Движение по кривой. Скорость. Ускорение. | Щербаков А. А.Скачать