Уравнения движения ла в перегрузках

Лекция 4
ПРИНЦИПЫ ОСУЩЕСТВЛЕНИЯ УПРАВЛЯЕМОГО ПОЛЕТА.
1. Уравнение движения ЛА в скоростной системе координат.
2. Маневренные свойства ЛА.
3. Способы создания управляющих сил и моментов
3.1 Газодинамические органы управления.
3.2 Аэродинамические органы управления.

ПРИНЦИПЫ ОСУЩЕСТВЛЕНИЯ УПРАВЛЯЕМОГО ПОЛЕТА.

1. Уравнение движения ЛА в скоростной системе координат.

2. Маневренные свойства ЛА.

3. Способы создания управляющих сил и моментов
3.1 Газодинамические органы управления.
3.2 Аэродинамические органы управления.

1. УРАВНЕНИЕ ДВИЖЕНИЯ ЛА В СКОРОСТНОЙ СИСТЕМЕ КООРДИНАТ.

Скоростная система координат позволяет анализировать силы и моменты, действующие на аппарат. Начало координат располагается в центре масс аппарата, ось ОХ совпадает с вектором скорости, ось ОY – перпендикулярна оси ОX и лежит в плоскости симметрии аппарата, ось OZ перпендикулярна плоскости ХОY и направлена таким образом, чтобы образовалась правая система координат.
Положение аппарата в этой системе координат характеризуется тремя углами:
1) углом атаки между продольной осью ОХ и проекцией вектора скорости ЛА на плоскость ОХY связанной системы координат;
2) углом скольжения между вектором скорости ЛА и плоскостью ОХY связанной системы координат;
3) углом крена между поперечной осью ОZ и осью OZg и нормальной системы координат, смещенной в положение, при котором угол рыскания равен нулю.

Рис. 1. К составлению уравнений движения ЛА

Общее движение аппарата упрощенно представляют в виде суммы двух слагаемых: движения центра масс ЛА и вращения вокруг его центра масс.
Для упрощения исследования движения ЛА рассмотрим его полет в вертикальной (рис. 1) плоскости.
На ЛА действуют аэродинамическая подъемная сила Ry; сила лобового сопротивления Rx, Р – тяга двигателя; mg – сила тяжести и аэродинамический момент Мz. Уравнения движения можно разбить на две группы: динамические и кинематические.
Динамические уравнения
( 1 )
где Iz, z – момент инерции и угловая скорость ЛА относительно оси ОZa; – угол наклона траектории; – угол атаки; m – масса аппарата, которая в общем случае изменяется по формуле:
( 2 )
где m0 – начальная масса; Iу – удельный импульс тяги; – полное время работы двигателя.
Два первых уравнения (1) устанавливают связь между силами, действующими на аппарат, и линейными ускорениями его движения: dV/dt – касательное, Vd/dt – нормальное ускорение (действительно, , где *– радиус кривизны траектории) и применяются при исследовании маневренных свойств ЛА.
Значение силы тяжести mg зависит от скорости и высоты полета аппарата. Для ЛА небольшой дальности, высоты и скорости влияние кривизны Земли на уравнение движения будет незначительным и его можно не учитывать, чего нельзя делать для баллистических и межконтинентальных ЛА, так как это может дать большие погрешности в расчетах.
Проанализируем влияние этих факторов.
Угловая скорость линии местного горизонта (рис. 2) определяется из уравнения:

( 3 )
Пропорционально AB на аппарат будет действовать центробежная сила, уменьшающая силу тяжести, т.е. в первых двух уравнениях системы (2.1) следует использовать:
( 4 )
где g0 – ускорение свободного падения на поверхности Земли.
Кинематические уравнения:
( 5 )
характеризуют траектории движения центра масс ЛА в земной системе ко-ординат.

Рис. 2. Влияние высоты полета ЛА на ускорение свободного падения.

2. МАНЕВРЕННЫЕ СВОЙСТВА ЛА.

При оценке эффективности ЛА его важным свойством является маневренность, которая определяется быстротой изменения вектора скорости. Очевидно, что для изменения величины и направления скорости полета необходимо иметь возможность изменить величину и направление равнодействующей всех сил. При рассмотрении уравнений сил в вертикальной плоскости получим Rx, Ry:
Nx=P+ Ry + Rx ( 6 )
проекции которой на оси Xa и Ya:
Nx=P cos- Rx;
Ny=P sin+ Ry.
Nx – управляющая касательная сила служит для изменения абсолютного значения вектора скорости: при Nx > mg sin скорость возрастает, при Nx = mg sin скорость постоянная, при Nx mg имеет место восходящая криволинейная траектория, при Ny = mg – прямолинейная, при Ny . Соответственно по величине нормальной перегрузки можно судить о характере траектории: nya cos вогнутость направлена вверх.
Аналогично можно сделать выводы и по другим случаям полета. Так, при полете в горизонтальной плоскости nya = 1, при горизонтальном прямолинейном равномерном полете nxa = 0, nya = 1, nza = 0.
При анализе движения ЛА различают два вида перегрузок: потребные и располагаемые.
Если известны все геометрические элементы траектории, то по формулам (12) можно определить перегрузки, которые должен иметь ЛА при движении по этой траектории. Эти перегрузки получили название потребных.
С другой стороны, ЛА при максимальном (предельно допустимом) отклонении органов управления в режиме балансировки может создавать перегрузки, которые получили название располагаемых. Эти перегрузки характеризуют маневренность аппарата, т. е. его способность создавать управляющие силы.
Очевидно, что для осуществления полета по требуемой траектории ЛА должен иметь располагаемые перегрузки, по крайней мере, не меньше потребных. В реальных условиях на ЛА действуют различные случайные факторы, обусловленные разбросом параметров атмосферы и ее турбулентностью, кро-ме того, геометрические параметры корпуса, крыльев, органов управления реализуются с определенной вероятностью при изготовлении. Это приводит к тому, что необходим определенный запас по перегрузке, т. е.
nрасп . (13)
в каждой точке траектории полета (рис. 3).

Рис. 3. Траектория движения ЛА:
1 – действительная; 2 – кинематическая

Продолжим анализ управляемого полета ЛА. Полет может быть установившимся (режим балансировки) и переходным (режим маневра) . При установившемся полете (с постоянной скоростью, на постоянной высоте, с постоянным углом атаки и т. д.) моменты тангажа, рысканья и крена равны нулю, и ЛА (как принято говорить) находится в режиме балансировки. Для продольной балансировки
mz + mz=0, (14)
где mz , mz – производные момента по углу атаки и углу отклонения ру-лей.
Для оценки балансировки обычно вводится понятие «статическая устойчивость ЛА», которое характеризует способность ЛА сохранять заданный режим полета при воздействии различных внешних возмущений. Степень статической устойчивости зависит от расстояния между центром масс xц.м и центром давления xц.д:

При х > 0 ЛА будет статически устойчив; чем больше значение х, тем быстрее ЛА возвращается в исходное положение. Поэтому с целью обеспечения большей устойчивости ЛА обычно увеличивают
В режиме маневра при отклонении органов управления, т. е. при переходе с одного установившегося полета в другой, происходит изменение параметров движения в течение некоторого промежутка времени. Для оценки этого режима вводится понятие «управляемость», которое характеризует способность ЛА совершать тот или иной маневр. Управляемость ЛА зависит от многих факторов, в том числе и от. При прочих равных условиях ЛА будет обладать большей управляемостью при возможно меньших значениях……

Скачать полную версию работы

СКАЧАТЬ работу l-raketostroenie/lekcii_raketostroenie_04.rar

Видео:Тренировка в центрифуге. Перегрузка в 7,6 G на лётчика.Скачать

И. В. Чепурных ДИНАМИКА ПОЛЁТА САМОЛЁТОВ

Юлия Обрютина 4 лет назад Просмотров:

1 Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Комсомольский-на-Амуре государственный технический университет» И. В. Чепурных ДИНАМИКА ПОЛЁТА САМОЛЁТОВ Утверждено в качестве учебного пособия Ученым советом Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Комсомольский-на-Амуре государственный технический университет» Комсомольск-на-Амуре 04

2 УДК (07) ББК я7 Ч-446 Рецензенты: В. М. Козин, доктор технических наук, профессор, заведующий лабораторией МД ФГБУН «Институт машиноведения и металлургии Дальневосточного отделения Российской академии наук»; Секция НТС филиала ОАО «Авиационная холдинговая компания «Сухой» «Комсомольский-на-Амуре авиационный завод имени Ю.А. Гагарина», секретарь НТС начальник НПО КнААЗ, главный научный сотрудник, кандидат технических наук, доцент Р. Ф. Крупский Чепурных, И. В. Ч-446 Динамика полёта самолётов : учеб. пособие / И. В. Чепурных. Комсомольск-на-Амуре : ФГБОУ ВПО «КнАГТУ», 04. с. ISBN Рассматриваются траекторные задачи: составляются уравнения движения центра масс летательного аппарата и на их основе рассчитываются основные лётные характеристики самолёта. Анализируется продольное движение самолёта: дополнительно составляются уравнения моментов и оцениваются статические характеристики продольной устойчивости и управляемости; линеаризуются уравнения движения и рассчитываются динамические характеристики продольной устойчивости и управляемости. Пособие предназначено для студентов, обучающихся по направлению подготовки «Авиа- и ракетостроение» и специальности «Самолёто- и вертолётостроение» при изучении ими дисциплины «Динамика полёта». УДК (07) ББК я7 ISBN ФГБОУ ВПО «Комсомольскийна-Амуре государственный технический университет», 04

3 ОГЛАВЛЕНИЕ ВВЕДЕНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС САМОЛЁТА Уравнения движения материальной точки в векторной форме Системы координат, применяемые в динамике полёта Скалярная форма записи уравнений движения центра масс летательных аппаратов Уравнения движения в перегрузках Исходные данные для интегрирования уравнений движения РАСЧЁТ ЛЁТНО-ТЕХНИЧЕСКИХ ХАРАКТЕРИСТИК САМОЛЁТА ДЛЯ УСТАНОВИВШИХСЯ РЕЖИМОВ ПОЛЁТА Диаграмма потребных и располагаемых тяг Установившийся набор высоты. Скороподъёмность летательного аппарата Установившееся снижение самолёта. Планирование Метод мощностей ДАЛЬНОСТЬ И ПРОДОЛЖИТЕЛЬНОСТЬ ПОЛЁТА Максимальные дальность и продолжительность полёта Радиус действия самолёта Влияние загрузки самолёта на его дальность ВЗЛЁТНО ПОСАДОЧНЫЕ ХАРАКТЕРИСТИКИ САМОЛЁТА Взлёт и начальный набор высоты Заход на посадку и посадка Прерванный и продолженный взлёт МАНЕВРЕННЫЕ ХАРАКТЕРИСТИКИ САМОЛЁТА Горизонтальная приемистость Криволинейный полёт в горизонтальной плоскости вираж Перегрузочная поляра Характерные маневры самолёта в вертикальной плоскости Петля Нестерова ПРОДОЛЬНАЯ СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ И БАЛАНСИРОВКА САМОЛЁТА Момент тангажа самолёта Аэродинамический момент тангажа крыла Аэродинамический момент тангажа фюзеляжа Аэродинамический момент тангажа гондол двигателей Момент тангажа двигателей Момент тангажа самолёта без горизонтального оперения Продольный момент горизонтального оперения

4 6.8. Демпфирующий момент тангажа, возникающий при вращении самолёта Продольная статическая устойчивость самолёта Продольная статическая устойчивость по перегрузке Продольная статическая устойчивость по скорости Продольная балансировка самолёта в горизонтальном полёте Балансировочная поляра Шарнирный момент органов продольного управления Усилие на ручке управления рулём высоты Статические характеристики продольной управляемости Выбор диапазона центровок и параметров горизонтального оперения ДИНАМИКА ПРОДОЛЬНОГО ВОЗМУЩЁННОГО ДВИЖЕНИЯ САМОЛЁТА Линеаризация уравнений движения самолёта Решение системы линейных дифференциальных уравнений с постоянными коэффициентами классическим методом Решение системы линейных дифференциальных уравнений с постоянными коэффициентами операторным методом Свободное продольное возмущённое движение самолёта Быстрая и медленная составляющие продольного возмущённого движения самолёта Собственное продольное короткопериодическое возмущённое движение самолёта Исследование управляемого движения самолёта с помощью передаточных функций и частотных характеристик Реакция самолёта в канале тангажа на ступенчатое отклонение руля высоты (стабилизатора) в короткопериодическом движении Реакция самолёта в канале тангажа на отклонение руля высоты (стабилизатора) по гармоническому закону в короткопериодическом движении Лётчик в системе управления летательным аппаратом Влияние конструктивных параметров самолёта и условий полёта на продольную устойчивость и управляемость ЗАКЛЮЧЕНИЕ. БИБЛИОГРАФИЧЕСКИЙ СПИСОК. 4

5 ВВЕДЕНИЕ Динамика полёта самолётов это раздел механики, в котором изучается движение летательных аппаратов (ЛА) в атмосфере. Ему также соответствует эквивалентное понятие «Аэромеханика самолёта». Эта дисциплина базируется на таких предметах, как теоретическая механика, аэродинамика, силовые установки, теория автоматического управления. В свою очередь, результаты, полученные в динамике полёта, используются в таких дисциплинах, как конструкция, прочность и проектирование самолётов, системы управления ЛА, их техническая эксплуатация. Создание современного самолёта невозможно без ясного понимания конструктором основ динамики полёта. С задачами динамики полёта ему приходится сталкиваться как на всех этапах проектирования ЛА, так и в процессе его эксплуатации. На этапе разработки технического предложения проводятся предварительные исследования различных аэродинамических схем и компоновок, оценивается возможность создания самолёта, удовлетворяющего заданным требованиям. Здесь первостепенное значение приобретают две задачи динамики полёта: ) расчёт основных лётно-технических характеристик (ЛТХ), к ним относят: диапазоны высот и скоростей, в которых возможен безопасный полёт ЛА и выполнение определённых полётных заданий; дальность и продолжительность полета, радиус действия; маневренные характеристики (радиус и время установившегося виража, скороподъёмность, время выполнения заданного маневра, потребный для маневра объём пространства и действующие при этом перегрузки и т.д.); взлётно-посадочные характеристики (ВПХ), куда входят скорость отрыва, посадочная скорость, длина разбега, длина пробега, взлётная дистанция, посадочная дистанция, характеристики прерванного и продолженного взлёта, класс аэродрома базирования и др. Помимо этих показателей в ЛТХ также включают ряд других величин, отражающих условия эксплуатации самолёта и не определяемых расчётами динамики полёта. ) расчёт статических характеристик устойчивости и управляемости самолёта (показатели продольной и боковой устойчивости и управляемости, балансировочные углы отклонения органов управления на различных режимах полёта и др.). На основе решения указанных задач определяются основные проектные параметры самолёта удельная нагрузка на крыло р, стар- G mg S S 5

6 P0 товая тяговооружённость P0, а также параметры аэродинамической m0 g компоновки (S го, S во, L го, L во, S рв, S рн, S эл ), безопасный диапазон (разбег) центровок самолёта и т.п. По мере разработки проекта и получения достоверной информации (продувки моделей в аэродинамической трубе) расширяется круг задач динамики полёта, усложняются математические модели. Например, на этапе эскизного проекта проводятся расчёты оптимальных траекторий полёта, определяются динамические характеристики самолёта как объекта управления, исследуются переходные процессы, проводятся комплексные исследования на имитационных стендах. Спроектированный с учётом требований безопасности для выполнения определённых задач в расчётных условиях самолёт изготавливается и проходит цикл лётных испытаний, в процессе которых его характеристики доводятся в соответствии с техническими требованиями и нормами, одновременно уточняются области эксплуатационных режимов и условий полёта. По результатам расчётов и испытаний составляется «Руководство по лётной эксплуатации» (РЛЭ), регламентирующее способы и условия эксплуатации самолёта. В ходе эксплуатации расчёты траекторий, оценка устойчивости и управляемости осуществляются при модификации самолёта, расширении области его использования, для повышения эффективности использования в изменившихся условиях, а также с учётом накопленного опыта.. УРАВНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС САМОЛЁТА Самолёт (ЛА) представляет собой систему деформируемых тел переменной массы, совершающих как общее переносное, так и взаимные относительные движения. При исследовании динамических свойств обычно применяют упрощённую модель самолёта как абсолютно твёрдого тела переменной массы. При расчёте ЛТХ самолёт рассматривают как материальную точку (используют только уравнения сил). При изучении вопросов устойчивости и управляемости самолёт рассматривают как материальное тело (используют уравнения сил и моментов). 6

7 .. Уравнения движения материальной точки в векторной форме Инерциальными системами отсчёта (ИСО) в классической механике называют те системы, по отношению к которым выполняется закон инерции (первый закон Ньютона). С весьма большой степенью точности ИСО можно считать гелиоцентрическую систему отсчёта. Любая система отсчёта, покоящаяся или движущаяся равномерно и прямолинейно относительно ИСО, сама является ИСО. Наоборот, всякая система, движущаяся ускоренно по отношению к ИСО, является неинерциальной. Геоцентрическая система не является ИСО по причине []: ) вращения вокруг своей оси с запада на восток с периодом Т = 3 ч 56 мин 4,09 с = 8664,09 с и угловой скоростью 5 7,9 0 с З (рис..). Вектор З направлен с юга на север; Т ) годичного обращения вокруг Солнца со средней скоростью движения по орбите 9,9 км/с; 3) нутационного колебания земной оси с периодом 8,6 года и амплитудой 9,»; 4) прецессионного движения относительно оси эклиптики с периодом лет; 5) движения вместе с солнечной системой относительно других звёзд. При исследовании полёта самолёта (ЛА) все эти составляющие движения, кроме первого, не учитываются. Если же скорость ЛА менее км/с (М 8 b сжатие, где b малая полуось общего земного эллипсоида. В некоторых задачах вместо общего земного эллипсоида используют 98,5 референц-эллипсоид. Так, на территории СНГ за размеры референцэллипсоида приняты размеры эллипсоида Красовского: а = м, а сжатие. Центр эллипсоида Красовского не совпадает с центром 98,3 масс Земли. Положение точки М в прямоугольной системе координат определяется радиус-вектором r (рис..3). Кинематическое уравнение [] Z Y О r Экваториальное сечение земного эллипсоида Рис. Геоид и общий земной эллипсоид М Рис..3. Положение точки М X d r, (.) dt где скорость материальной точки. Это уравнение справедливо для любой системы отсчёта. Изменение скорости материальной точки переменной массы в неинерциальной системе отсчёта определяется динамическим уравнением d m( t ) dt Экваториальное сечение геоида P F J пер J кор, (.) где Р главный вектор реактивных сил; F главный вектор внешних сил (кроме реактивных); J пер и J кор переносная и кориолисова силы инерции. 8

9 Для описания движения центра масс (ц.м.) ЛА относительно вращающейся Земли перепишем уравнение (.) в виде d m( t ) P R G J кор, (.3) dt где R главный вектор аэродинамических сил; G вектор силы тяжести; J m. кор З При скоростях полёта ЛА менее км/с сила Кориолиса J кор 10 Нормальная система координат ОХ g Y g Z g (рис..5) это подвижная система координат, начало которой помещено в ц.м. ЛА, ось ОY g направлена вверх по местной вертикали, оси ОХ g и ОZ g лежат в горизонтальной плоскости, их направление выбирается в соответствии с решаемой задачей. Обычно ось ОХ g направлена на север по касательной к географическому меридиану, а ось ОZ g направлена на восток по касательной к географической параллели. Точка пересечения А радиус-вектора r с поверхностью Земли определяет географические (сферические) координаты ЛА λ и φ, описывающие трассу полёта. Здесь λ географическая долгота (отсчитывается от гринвичского меридиана на восток), φ географическая широта (отсчитывается от плоскости экватора), r расстояние от центра Земли до ЛА. Рис..5. Нормальная система координат ОХ g Y g Z g и её положение относительно земной системы: плоскость экватора; местная горизонтальная плоскость, проходящая через точку О; 3 параллель, проходящая через точку А; 4 меридиан, проходящий через точку А Стартовая и нормальная системы координат в общем случае вращаются вместе с Землей. В дальнейшем будем считать их невращающимися. Это допущение при скоростях полёта ЛА менее км/с не вносит большой погрешности в расчёт ЛТХ. В связанной системе координат ОХYZ (рис..6) оси координат совпадают с главными осями инерции ЛА. Плоскость ОХY является плоскостью симметрии ЛА. Направление продольной оси ОХ должно специально оговариваться. Обычно ось ОХ параллельна средней аэродинамической хорде крыла и направлена от хвостовой к носовой части ЛА. 0

11 Рис..6. Связанная система координат ОХYZ Связанная система координат жёстко фиксирована по отношению к ЛА и её положение относительно нормальной системы координат определяет пространственное положение ЛА. Оно характеризуется эйлеровыми углами рыскания, тангажа и крена (рис..7). Рис..7. Связанная система координат ОХYZ и её ориентация относительно нормальной системы координат ОХ g Y g Z g : местная горизонтальная плоскость; плоскость симметрии ЛА; 3 вертикальная плоскость, содержащая ось ОХ

12 Углом рыскания ψ (пси строчная) называют угол между осью ОХ g и проекцией продольной оси ОХ на горизонтальную плоскость ОХ g Z g. Угол тангажа (тэта строчная) это угол между осью ОХ и горизонтальной плоскостью ОХ g Z g. Угол тангажа положителен, если ось ОХ находится выше горизонтальной плоскости. Угол крена γ это угол между осью ОY и вертикальной плоскостью, содержащей продольную ось ОХ. Движение ц.м. ЛА определяется линейными скоростями: воздушной, земной к и путевой п. Если воздух неподвижен, то векторы воздушной и земной скоростей совпадают. При наличии ветра, имеющего скорость W, к W. Путевая скорость п это проекция земной скорости к на горизонтальную плоскость ОХ g Y g. Воздушная скорость играет основную роль в создании аэродинамических сил и моментов, а земная и путевая скорости используются при решении навигационных задач. В скоростной системе координат ОХ а Y а Z а (рис..8) ось ОХ а совпадает по направлению с вектором воздушной скорости, ось подъёмной силы ОY а перпендикулярна оси ОХ а и лежит в плоскости симметрии ЛА, боковая ось ОZ а образует с другими осями правую систему координат. Положение ЛА относительно воздушного потока определяется углами атаки α и скольжения β, задающими взаимную ориентацию связанной и скоростной систем координат. α β α п Рис..8. Скоростная система координат ОХ а Y а Z а и её ориентация относительно связанной системы координат ОХYZ

13 Угол атаки α это угол между продольной осью ОХ и проекцией воздушной скорости на плоскость симметрии ЛА. Угол скольжения β измеряют между вектором воздушной скорости и плоскостью симметрии ЛА. В некоторых случаях рассматривают пространственный угол атаки α п это угол между осью ОХ и вектором воздушной скорости. По отношению к нормальной системе координат скоростная система координат повёрнута на скоростные углы рыскания, тангажа и крена ψ а, а и γ а, введённые по аналогии с эйлеровыми углами ψ, и γ для связанной системы координат (рис..9). Рис..9. Взаимная ориентация скоростной ОХ а Y а Z а и нормальной ОХ g Y g Z g систем координат: местная горизонтальная плоскость; вертикальная плоскость, содержащая вектор воздушной скорости Траекторная система координат ОХ к Y к Z к (рис..0) определяется так: ось ОХ к направлена по вектору земной скорости к, ось ОY к лежит в вертикальной плоскости, проходящей через вектор к, и направлена вверх от поверхности Земли, ось ОZ к образует с другими осями правую систему координат. Ориентация траекторной системы координат относительно нормальной определяется двумя углами: углом пути и углом наклона траектории. Угол пути Ψ (пси заглавная) это угол между проекцией земной скорости к на местную горизонтальную плоскость ОХ g Y g (путевой скоростью п ) и осью ОХ g. 3

14 Угол наклона траектории Θ (тэта заглавная) образован направлением земной скорости к и местной горизонтальной плоскостью ОХ g Y g. Y g Рис..0. Траекторная система координат ОХ к Y к Z к и её положение относительно нормальной системы координат ОХ g Y g Z g : местная горизонтальная плоскость; вертикальная плоскость, содержащая вектор земной скорости Для перехода от одной системы координат к другой пользуются таблицей направляющих косинусов. (см. ГОСТ [3]). X g 4

15 Таблица направляющих косинусов Таблица. Нормальная система координат 5

16 Связанная система координат Продолжение табл.. Примечание. Для траекторной системы соотношения даны без учета ветра. При наличии ветра использовать С, С, С или двойной переход от связанных осей к траекторным через нормальные Примечание. Без ветра. При наличии ветра использовать двойной переход от скоростной к траекторной системе через нормальную 6

17 .3. Скалярная форма записи уравнений движения центра масс летательных аппаратов Уравнения (.4) нельзя использовать непосредственно для расчёта траекторий и ЛТХ ЛА. Их необходимо записать в скалярной форме. Обычным методом перехода является запись уравнений (.4) в проекциях на три взаимно перпендикулярных направления, заданных единичными ортами i, j, k, которые образуют оси той или иной системы координат. Выбор системы координат диктуется соображениями простоты записи уравнений движения и сил для решения конкретных задач. Например, при расчёте ЛТХ динамическое уравнение рассматривают в проекциях на оси траекторной системы координат, а кинематическое уравнение в проекциях на оси нормальной системы координат. Кроме того, реактивные силы задаются в связанной системе координат, а аэродинамические силы в скоростной системе координат. Для определения изменения положения ц.м. ЛА в зависимости от скорости спроецируем кинематическое уравнение системы (.4) на оси нормальной системы координат, используя таблицы направляющих косинусов: d r ; r ( x,, ) g g g в нормальной системе координат; dt (, 0, 0) в траекторной системе координат. Спроецируем отрезок, лежащий на оси ОХ к, по осям ОХ g, ОY g, ОZ g. Направляющие косинусы (cosψ cosθ, sinθ, sinψ cosθ). Тогда x g g g dl L cosψ cosθ; dt dh H sinθ; dt sinψ cosθ. (.5) При отсутствии ветра ( к ) оси ОХ а и ОХ к совпадают, угол пути совпадает со скоростным углом рыскания (Ψ = ψ а ), а угол наклона траектории равен скоростному углу тангажа (Θ = а ). Кроме того, если известны углы ψ, и γ, определяющие пространственное положение самолёта, а также углы Ψ и Θ, определяющие направление скорости его ц.м. относительно нормальной системы координат, то через них можно однозначно вычислить угол атаки α, угол скольжения β и скоростной угол крена γ а. Определяя из табл.. косинусы углов между связанными и нормальными осями, а также между скоростными и нормальными осями, по- 7

18 сле преобразований получим требуемые тригонометрические соотношения. Например, для угла скольжения β имеем: cos( Z, X ) sin k i k cos( X, X ) ig g cos( X cos( X, Z ) k cos( X, X ) cos( Z, X ) cos( X, Y g g g ) cos( Z, Y g g ) cos( X, Z g g, Y ) j g ) cos( Z, Z или sin cossin sin cos( ) cossin( ) sin cossin (.6) Рассуждая аналогично, получим sin (sin cos cos( ) sin sin( )) cos cos sin coscos ; (.7) sin cos cos sin sin cos (sin sin cos cossin ). (.8) Вектор угловой скорости самолёта, получающийся за счёт вращения ЛА относительно связанных осей при отклонении рулей и элеронов, равен геометрической сумме угловых скоростей элементарных поворотов, т.е. x. (.9) Уравнение (.9) это кинематическое уравнение вращательного движения самолёта в векторной форме. Проецируя векторы, и на оси связанной системы координат ОХYZ с помощью табл. получим sin x ; cos cos sin ; cossin cos. Обычно аргументами в данных выражениях являются проекции угловой скорости ω х, ω и ω, задаваемые через углы отклонения рулей и элеронов. Решая последние уравнения относительно, и, найдём искомые кинематические соотношения: d dt у sin cos ; (.0) g ) g 8

19 d dt x d sec( dt tg ( cos sin ) ; (.) у у cos sin ). (.) Если система ортов i, j, k, привязанная к материальной точке, вращается относительно неподвижной системы координат с угловой скоростью, а сама материальная точка движется со скоростью относительно той же неподвижной системы координат, то в динамическом уравнении системы (.4) необходимо использовать выражение для полной производной вектора [4]. Например, если i j k, тогда d dt d i dt x d j dt d k dt di dt x x d j dt dk dt t δ где локальная производная, характеризующая быстроту изменения δ t di d j d k модуля вектора скорости ; i ; j ; k. dt dt dt При движении ц.м. ЛА траекторная система координат вращается относительно нормальной системы с угловой скоростью к, проекции которой на оси ОХ к, ОY к и ОZ к составят хк sin ; к cos ; к. (.3) Спроецируем динамическое уравнение системы (.4) на вращающиеся оси траекторной системы координат ОХ к, ОY к и ОZ к m( t) к P R G t. (.4) Векторы в левой части уравнения имеют проекции в траекторной системе координат, 0, 0;, 0, 0. Тогда с учётом (.3) получим t, к i x хк j ук k к i ук к j x xк к k x xк к j cos k 0 i ; 9

20 0,, к cos. Рассмотрим векторы в правой части уравнения (.4). Тяга силовой установки Р обычно лежит в плоскости симметрии самолёта XOY и составляет угол φ p с положительным направлением оси OX. Используя таблицу направляющих косинусов. между осями связанной и траекторной систем координат, найдём проекции тяги на оси траекторной системы координат Р P cos( ) cos Р Р ук к хк p ; P sin( )cos cos( )sinsin ; (.5) p p P sin( )sin cos( )sincos. Проекции аэродинамической силы R на оси траекторной системы координат выражаются через проекции на скоростные оси R R R ; ахк Х а аук ак Y Y а а p p cos Z sin ; (.6) sin Z cos. Вектор G имеет следующие проекции (рис..): Y g Θ Y к X к Θ mgsinθ X g mgcosθ Θ G= mg Рис. Вектор G и его проекции G G G xк к к mg sin ; mg cos; 0. (.7) 0

21 Таким образом, векторное уравнение (.4) эквивалентно трём скалярным уравнениям m Fхк Pхк Rахк Gхк ; m Fук Pук Rаук G m cos Fк Pк R к ак ; G Здесь проекции сил определяются уравнениями (.5) (.7), т.е. F Pcos( )cos X mg sin F хк p ; ук P sin( )cos cos( )sinsin Y cos Z sin mg cos ; F к p p )sin cos( p )sin cos Y sin Z cos p к. (.8) P sin(. Первое уравнение системы (.8) определяет изменение модуля скорости ц.м. ЛА, второе и третье изменение кривизны траектории соответственно в вертикальной и горизонтальной плоскостях. В курсе «Динамика полёта» в основном рассматривают частные полётные случаи, а именно: ) полёт в вертикальной плоскости без крена и скольжения, при этом β = 0; γ = 0; ψ = Ψ и = α + Θ; б) полёт в горизонтальной плоскости без крена с малыми углами атаки, при этом Θ = 0; γ = 0; sinα 0; cosα ; cos ; = α; β = ψ Ψ; в) полёт без скольжения с малыми углами атаки, тогда β = 0; sinα 0; cosα ; Θ и γ а = γ (при отсутствии ветра)..4. Уравнения движения в перегрузках Введём понятие перегрузки, широко применяемое в динамике полёта. Перегрузкой называется геометрическая сумма всех сил, действующих на ЛА, за исключением силы тяжести, отнесённая к величине силы тяжести [, 4] P R P R n. (.9) G mg Перегрузка это вектор, обычно раскладываемый по осям скоростной системы координат. Тангенциальная перегрузка n xа совпадает с вектором скорости, нормальная перегрузка n а направлена по оси подъёмной силы Y, боковая перегрузка n а совпадает с осью О Z а. Запишем (.9) в скалярной форме. Полагаем, что вектор тяги Р имеет проекции в связанной системе координат (Рcosφ p, Рsinφ p, 0), а вектор

22 аэродинамических сил R имеет проекции в скоростной системе координат ( X, Y, Z ). Применив таблицу направляющих косинусов., получим n n n xа а а P cos( р )cos X mg Psin( mg P cos( р )sin Z mg р ) Y ; ;. (.0) Используя эти выражения и таблицу направляющих косинусов., запишем вектор перегрузки в проекциях на оси траекторной системы координат (при отсутствии ветра) n n n xк к к n n n xа а а ; cos sin n n а а sin ; cos. С учётом (.7) и (.0) уравнения (.8) примут вид m P cos( )cos X mg sin n mg mg sin ; р g nxа sin ; g n а cos nа sin cos; (.) g n а sin nа cos. cos Уравнения (.) называют уравнениями движения в перегрузках, они определяют изменение вектора скорости по величине и направлению в зависимости от действующих на ЛА перегрузок. Девять кинематических уравнений (.5), (.6) (.8), (.0) (.), а также три динамических уравнения в форме (.8) или (.) описывают пространственное движение ц.м. самолёта. К ним добавляют уравнение расхода масс dm Р с m PR сек. (.) dt 3600 где β сек секундный расход топлива; с PR удельный часовой расход топлива с учётом дросселирования двигателей. В итоге получают систему из тринадцати обыкновенных нелинейных дифференциальных уравнений, интегрирование которой в общем случае производится численными методами. x

23 .5. Исходные данные для интегрирования уравнений движения Для решения уравнений движения должны быть заданы аэродинамические характеристики самолёта (зависимости с уа = с уа (α,м) и с ха = с ха (α, М) (рис..), а также поляры с уа = с уа (с ха, М) (рис..3) в крейсерской, взлётной и посадочной конфигурациях), характеристики силовой установки (дроссельные с PR (R) (рис..4), тяговые высотно-скоростные Р(М, Н) (рис..5), расходные высотно-скоростные с P (М, Н) (рис..6)), а также абсолютные (G 0 взлётный вес ЛА, S площадь крыла, Р 0 стартовая тяга) или относительные параметры самолёта (удельная нагрузка на крыло р G S, стартовая тяговооружённость P0 P0 G0 ), ограничения режимов полёта (рис..7), начальные значения параметров движения ( 0, Θ 0, Ψ 0, L 0, H 0, Z 0 ). с уа с ха Рис. Типовые зависимости с уа =с уа (α) и с ха =с ха (α) Рис..3. Типовая поляра с уа = с уа (с ха ) с PR 0 R Рис..4. Дроссельная характеристика силовой установки 3

24 Н 0 25 Н, км Рис..7. Эксплуатационный диапазон высот и скоростей полёта ЛА с учётом ограничений: ограничение по min ; ограничение по mx ; 3 ограничение по переносимости человеком болтанки; 4 ограничение по прочности конструкции при болтанке; 5 ограничение по предельному скоростному напору для конструкции; 6 ограничение по кинетическому нагреву конструкции Расчёт и сравнение лётных данных и характеристик движения самолётов проводят для значений термодинамических параметров воздуха (p H, T H, ρ H, H ), соответствующих на данной высоте стандартной атмосфере (МСА или ISA), определяемой по ГОСТ [5].. РАСЧЁТ ЛЁТНО-ТЕХНИЧЕСКИХ ХАРАКТЕРИСТИК САМОЛЁТА ДЛЯ УСТАНОВИВШИХСЯ РЕЖИМОВ ПОЛЁТА В основе этого расчёта лежит метод тяг Н. Е. Жуковского [, 4, 6, 7]. Его идея заключается в сравнении потребного значения тяги Р п для осуществления выбранного режима полёта с располагаемым значением тяги Р р, которое обеспечивает установленная на самолёте силовая установка. При расчёте ЛТХ самолёта принимают следующие допущения: ) движение самолёта (ЛА) происходит в вертикальной плоскости без крена и скольжения (γ а = β = = 0); ) набор высоты и снижение осуществляются по равновесным траекториям, близким к прямолинейным, с малыми углами Θ (cosθ ; 0 ; n а = ); 5 0, км/ч

26 3) режимы движения характеризуются малыми углами атаки (P cos(α + φ р ) P; P sin(α + φ р ) 27 С учётом (.) уравнения (.3) примут вид Р ; G mg ; п X а Y mg Р п, (.4) к где к аэродинамическое качество самолёта (ЛА) на данном режиме полёта. Последовательность расчёта Р п при фиксированных значениях М() и Н такова. Сначала из второго уравнения системы (.4) определяем mg mg су, затем по поляре находим с ph M х и, наконец, 0,7 S H S H вычисляем Рп сх 0,7 рн М S сх S. На рис.. показан совмещённый график потребной и располагаемой тяг для заданной высоты при определённых массе самолёта (ЛА) и условиях полёта. Р р P п Н=const Р р II режимы I режимы α кр α доп P п P п min α эк α нв 0 св эк min нв кр mx (М) Рис. Кривые потребной P п и располагаемой Р р тяги Здесь указано несколько характерных скоростей горизонтального полёта: св скорость сваливания, соответствующая углу атаки α = α кр (с у = с у mx ); min практическая минимальная скорость, определяемая углом атаки 7

28 α доп α кр 3 0 (с удоп (0,8 0,85 )с уmx ); эк экономическая скорость полёта на экономическом угле атаки α эк, при этом потребная мощность минимальна (полет с такой скоростью является наиболее продолжительным, практически же скорость такого полета больше скорости экономической, экономическая скорость равна примерно 0,75 наивыгоднейшей скорости); нв наивыгоднейшая скорость, соответствующая минимальной потребной тяге (полёт на максимальном аэродинамическом качестве кmx ( с у сх ) mx ); кр крейсерская скорость, определяемая минимальным отношением потребной тяги к скорости (при слабой зависимости удельного расхода топлива от скорости полёта близка к режиму минимального километрового расхода топлива или крейсерскому режиму, обеспечивающему максимальную дальность полёта); mах максимальная скорость горизонтального установившегося полёта на данной высоте. Скорость нв делит скоростной диапазон полётов на данной высоте на две части: справа от нв имеем так называемые I режимы, слева от нв так называемые II режимы. На I режимах самолёт устойчив по скорости, на II режимах неустойчив по скорости. Полёт на II режимах нежелателен, так как в этом случае усложняется пилотирование самолёта, что при близости к критическому углу атаки небезопасно. Опасность повышается ещё и из-за того, что на малых скоростях самолёт сравнительно быстро её теряет. При полёте на II режимах непроизвольное изменение скорости (например, при воздействии ветра), нарушает равновесие сил, которое без вмешательства пилота уже не восстанавливается на прежней скорости. Поскольку полёт дозвукового неманевренного самолёта на вторых режимах нежелателен, то, практически, минимальной скоростью горизонтального полёта является нв. Как правило, полёт на II режимах при нормальной эксплуатации самолёта имеет место только на этапе посадки. У сверхзвуковых самолётов возможны две области I режимов и две области II режимов полёта, по одному в дозвуковой и сверхзвуковой зонах (рис..3). II режим в сверхзвуковой зоне из-за сравнительно медленного изменения скорости и сохранения хорошей управляемости самолёта опасности для пилотирования не представляет. На больших высотах полёт сверхзвукового самолёта выполняется, как правило, на вторых режимах. Обычно на одном графическом поле строят семейства кривых потребных и располагаемых тяг для нескольких высот (рис..4). 8

29 Р р P п Н=const Р рф Р р 0 P п II режимы I режимы II режимы I режимы Рис..3. Зоны первых и вторых режимов для сверхзвукового самолёта М Рис..4. Семейства кривых потребных и располагаемых тяг 9

30 .. Установившийся набор высоты. Скороподъёмность летательного аппарата Запишем уравнения (.) для установившегося набора высоты ( 0) n xа = sinθ ; n а =. (.5) P X Pр Р п P Из (.5) получим sin nxа. (.6) mg mg mg А из (.6) следует, что для подъёма по наиболее крутой траектории полёт необходимо совершать при скорости нв, когда избыточная тяга ΔР максимальна. Вертикальная скорость самолёта Θ P N H sin, (.7) mg mg где ΔN=N p N п избыточная мощность. При максимальной избыточной мощности (ΔN= ΔN mx ) вертикальная скорость максимальна ( = mx ). Для дозвуковых ЛА это соответствует скорости на 0 30 % больше нв. Кривые скороподъёмности для дозвукового и сверхзвукового самолётов приведены на рис..5 и.6. у, м/c уmxн0 Н 0 Н 0 31 у, м/c Н 0 Н 0 32 Отсюда dh dh H dt dt. H t 0 tmin dh H ; dh 0 mx. (.8) Графическая зависимость высоты Н от минимального времени её набора называется барограммой подъёма (рис..8). Это название сложилось исторически и объясняется тем, что первоначально данная кривая вычерчивалась барографом, т.е. барометром-самописцем. H, км H ст 0 Рис..8. Барограмма подъёма t min Дальность при установившемся наборе высоты найдём из уравнения Θ dl наб tg dн dh dl наб sin dh dh mg dlнаб. n P xа Отсюда Н dh mg Н dh Lнаб mg. (.9) P P Установившееся снижение самолёта. Планирование Если Р р 33 При планировании, когда маршевая силовая установка не работает или находится в режиме «малый газ», Р р = 0 и тогда Обычно угол Θ пл мал, поэтому Рп Х а sin пл. mg mg к пл sin пл tgпл. (.0) к Lпл пл к ( Н Н L пл mx кmx ( Н Н. (.) Отсюда Lпл к Н ) и ) Скорость установившегося планирования пл mg cos с S упл Н пл Н. (.) Эта скорость зависит от высоты, поэтому планирование на постоянных α пл и Θ пл не является строго установившимся и должно рассматриваться как квазиустановившееся. Таким образом, формулы (.7) (.) полностью описывают квазиустановившееся движение самолёта в вертикальной плоскости при наборе высоты и снижении..4. Метод мощностей Для самолётов с винтовыми или вентиляторными движителями расчёт ЛТХ обычно проводят по методу мощностей, поскольку характеристики двигателей таких ЛА (ПД, ТВД или ТВлД) задаются в зависимости от их мощности. Вместо графиков потребных и располагаемых тяг строят графики потребных и располагаемых мощностей (рис..9). Рис..9. Семейства потребных и располагаемых мощностей Ан-4 33

34 3. ДАЛЬНОСТЬ И ПРОДОЛЖИТЕЛЬНОСТЬ ПОЛЁТА Дальностью полёта называется расстояние L, проходимое самолётом по горизонтали, при израсходовании определённого запаса топлива (рис. 3.) L L L L. наб кр сн L L наб L кр L сн Рис. 3.. Типовой профиль полёта на дальность Крейсерский этап полёта это часть полёта с постоянной скоростью на постоянной высоте или постоянном эшелоне (диапазоне) высот. Имеющийся на борту запас топлива целиком не расходуется на крейсерский этап, так как часть топлива идёт на запуск и прогрев двигателей, рулёжку самолёта по аэродрому и взлёт, на набор высоты, снижение и посадку самолёта. Оставшуюся после выполнения данных процедур часть топлива будем называть располагаемым запасом топлива m Т.расп. При оценке дальности полёта различают понятия технической и практической дальности полёта [, 4, 6, 7, 8]. Технической дальностью называют расстояние, проходимое самолётом в условиях полного безветрия при израсходовании всего располагаемого запаса топлива и при условии, что траектория полёта лежит в одной и той же вертикальной плоскости. Практической дальностью называют расстояние по горизонтали, проходимое самолётом при израсходовании располагаемого запаса топлива, за исключением аэронавигационного запаса (АНЗ) топлива массой m Т.АНЗ. В соответствии с нормами лётной годности самолётов АП-3 и АП-5 [9, 0] m Т.АНЗ должна обеспечить полёт самолёта на режиме нв (к=к mx ) в течение мин. Часовой расход топлива mg qч сpr Pп сpr, кг/ч. (3.) к Километровый расход топлива qчас Pп mg qкм сpr сpr, кг/км. (3.) 3,6 3,6 3,6 к 34

35 В формулах (3.) и (3.) к полётное аэродинамическое качество самолёта с учётом потерь на балансировку. Дифференциальные уравнения расхода масс dm dm q км ; qч. (3.3) dl dt Интегрируя уравнения (3.3), получим m m dm 3,6 к dm L кp, км; (3.4) m qкм g m сpr m m m dm к dm T кp, ч. m qчас g m сpr m Здесь m=m 0 m Т.взл m Т.наб масса топлива в начале крейсерского этапа полёта (точка на рис. 3.); m 0 взлётная масса самолёта; m Т.взл масса топлива, необходимая для запуска и прогрева двигателей, руления и взлёта самолёта; m Т.наб масса топлива, необходимая для набора крейсерской высоты полёта; m=m m Т.расп масса топлива в конце крейсерского этапа полёта (точка на рис. 3.) при расчёте технической дальности полёта; m=m m Т.расп +m Т.АНЗ масса топлива в конце крейсерского этапа полёта (точка на рис. 3.) при расчёте практической дальности полёта. к Подынтегральная функция в формуле (3.4) называется с PR параметром дальности. 3.. Максимальные дальность и продолжительность полёта Подынтегральные выражения в данных формулах являются сложными функциями (M), и Н и поэтому для получения максимальной дальности или продолжительности полёта для каждого конкретного типа самолёта рассчитывают программы полётов по оптимальным траекториям. 3,6 m к dm L кp.mx ; g m сpr m mx m к dm T кp.mx. g m сpr m mx В первом приближении можно принять подынтегральные функции не зависящими от полётной массы m и тогда 35

36 3,6 к m Lкp.mx ln ; (3.5) g сpr m T к g с mx m ln m кp.mx. PR mx Рассмотрим влияние ветра на дальность полёта. При наличии ветра, имеющего попутную или встречную составляющую скорости W, километровый расход топлива будет равен q км qчас с 3,6 PR Pп 3,6 W q км( W 0) W и тогда Lкp Lкp( W 0). W Для грубых прикидок можно принять: для достижения максимальной дальности крейсерский полёт необходимо осуществлять на высотах ниже статического потолка на 3 км при скорости = кр ; для достижения максимальной продолжительности полёта его необходимо осуществлять на высотах ниже статического потолка на км при скорости = нв. 3.. Радиус действия самолёта Когда полётное задание предусматривает не перелёт самолёта с одного аэродрома на другой, а возвращение самолёта на аэродром базирования после выполнения заданной операции в зоне применения (рис. 3.), то в этом случае вводят понятие радиуса действия самолёта R. Радиус действия, как и дальность, также может быть техническим и практическим. Аэродром базирования m m m сн R R m х m х m сн Зона применения Рис. 3.. К определению радиуса действия R 36

37 Для его вычисления применим формулу (3.5). Имеем 3,6 к R g сpr mx m ln mx 3,6 к g сpr mx mx m ln m m сн сн m mx mсн или ln ln. mx m mсн где m сн масса сбрасываемой нагрузки. Решая последнее уравнение относительно m х, получим m mсн mсн x m m m Подставив (3.6) в (3.5), окончательно находим 3,6 к R g сpr mx ln m сн m сн m сн m m m. (3.6) При постоянно действующем в одном направлении ветре, имеющем составляющую скорости W по линии полёта, радиус действия уменьшается, независимо от направления этой составляющей и будет равен W R R ( W 0) Влияние загрузки самолёта на его дальность Техническая и практическая дальности, как и радиус действия, зависят от массы самолёта, а также от массы целевой нагрузки (ц.н.). Рассмотрим эту зависимость в графическом виде (рис. 3.3). Если m цн = 0, то L = L mx. При увеличении m цн и неизменной заправке топливом m Т =const (участок диаграммы) дальность монотонно уменьшается. При этом растёт взлётная масса m 0. Однако этот рост ограничивается пред величиной m 0, определяемой возможностью эксплуатации с аэродромов расч пред данного класса, т.е. m m m m, отсюда расч цн пред m0 пуст T цн 0 m m 0 mпуст mt. Это соответствует точке b на диаграмме. При этом получаем расчётную дальность L расч. сн. 37

38 m цн, кг пред m цн расч m цн d 3 c b 0 Если и далее продолжать увеличение m цн, то это возможно только за счёт такого же уменьшения массы топлива, что приводит к более интенсивному падению дальности (участок диаграммы). При проектировании самолёта задаётся предельное значение m пред цн L расч, определяемое вместимостью отсеков самолёта, эксплуатационными или иными соображениями (участок 3 диаграммы). Обычно самолёт эксплуатируется в области, ограниченной заштрихованным прямоугольником на диаграмме, что связано с требованиями безопасности полётов. Если самолёт необходимо эксплуатировать на дальностях свыше L mx, то используют подвесные топливные баки (ПТБ), сбрасываемые в полёте после выгорания топлива, или применяют дозаправку самолёта в воздухе от самолёта-танкера (заправщика). 4. ВЗЛЁТНО ПОСАДОЧНЫЕ ХАРАКТЕРИСТИКИ САМОЛЁТА Взлёт и посадка самолёта являются наиболее сложными и ответственными этапами полёта [8]. Ошибки пилотирования на них зачастую заканчиваются трагически, поскольку времени и запаса высоты для их исправления практически нет. Дополнительной нагрузкой для лётчика является изменение аэродинамических характеристик самолёта, вызванное влиянием близости земли. Расчёт ВПХ ведётся для нескольких вариантов состояния атмосферы, в том числе: а L mx Рис Зависимость дальности полёта от массы целевой нагрузки L, км 38

39 для стандартных условий (МСА) Н = 0; Т = 87К (5 0 С); ρ =,5 кг/м 3 ; р=035 Па; для расчётных условий (РУ) Н = 0; Т = 303К (30 0 С); ρ =, кг/м 3 ; р = Па; для самых неблагоприятных атмосферных условий, в которых может находиться проектируемый самолёт в процессе его эксплуатации, например, летняя тропическая атмосфера и значительная высота аэродрома над уровнем моря. 4.. Взлёт и начальный набор высоты Этап взлёта начинается с разбега самолёта по взлётно-посадочной полосе (ВПП) и заканчивается достижением скорости, высоты и конфигурации самолёта, необходимых для начала полёта по маршруту. Для гражданских самолётов высота начала полёта по маршруту устанавливается Авиационными Правилами АП-3, АП-5 [9,0] и составляет 400 м над уровнем ВПП (рис. 4.). Рис. 4.. Взлёт и начальный набор высоты 39

40 Схема собственно взлёта приведена на рис. 4.. = 0 Х а N Y а Р = отр = H F тр L раз G 0 L вув На высоте Н = 0,7 м (35 ft) безопасная скорость самолёта должна, как минимум, на 0 % превышать скорость сваливания во взлётной конфигурации. В целях безопасности полёта до высоты 0 м не допускается изменение конфигурации крыла. Начиная с высоты 0 м и разгона до скорости, на 0 % превышающей скорость сваливания в крейсерской конфигурации, происходит поэтапное изменение конфигурации крыла от взлётной к крейсерской. Одновременно продолжается набор высоты. По достижении высоты 400 м и крейсерской конфигурации взлёт считается закончившимся, работу двигателей переводят со взлётного режима на номинальный, и начинается этап набора крейсерской высоты полёта. По возможности взлёт самолёта осуществляется против ветра. Боковая составляющая скорости ветра затрудняет выполнение взлёта и для каждого самолёта в Руководстве по лётной эксплуатации (РЛЭ) задаётся её предельная величина. Скорость отрыва отр,05, св, где св скорость сваливания во взлётной конфигурации. Эту скорость найдём из условия Y = G 0 = m 0 g или св m0g с mx S m0g св ; c S отр L взл Рис. 4.. Схема собственно взлёта mx m0g, ;, св, (4.) c S mx где с у mx максимальный коэффициент подъёмной силы самолёта во взлётной конфигурации. Для расчёта длины разбега запишем уравнения движения самолёта по ВПП dl L d ; Y N m 0 g ; m0 P X Fтр, (4.) dt dt 40

41 где N реакция на шасси со стороны ВПП; Р тяга двигателей; F f N f m g c S тр тр. раз тр. раз 0 ураз сила трения при движении по ВПП. Коэффициент силы трения при разбеге f тр.раз определяется качеством и состоянием ВПП, характеристиками колёс шасси и изменяется от 0,0 для сухого бетонного покрытия до 0, для мокрого травяного покрова или заснеженной ВПП. Из последнего уравнения (4.) получим c S f m g с S d P X F P храз тр. раз 0 ураз тр g. dt m0 m0g m0g m0g В правой части уравнения сгруппируем слагаемые, содержащие, d P S g fтр. раз c храз fтр. разсураз. (4.3) dt m0g m0g Если принять допущение о том, что в процессе разбега неизменны тяга двигателей Р и угол атаки α (с храз = const ; с ураз = const), то из (4.3) получим d dt L L раз раз d dl omp 0 g dl dt g omp 0 а d dl P m раз dl f d d dt c L d раз omp 0 d d dt тр. раз храз тр. раз ураз 0g d b раз где а раз и b раз постоянные: а раз f тр. раз m0g, P S ; bраз c храз fтр. разсураз. m g f с 0 ; ; S m0g Последний интеграл является табличным. Взяв его, приходим к выражению а раз Lраз ln. (4.4) gb а b раз раз раз отр 4

42 При наличии ветра, имеющего составляющую скорости W вдоль ВПП, W L ( 0) раз Lраз W. (4.5) отр Если ветер попутный, то в (4.5) используем знак +, при встречном ветре используем знак. Взлётной дистанцией называется расстояние, проходимое самолётом по горизонтали с момента страгивания до набора высоты Н и безопасной скорости взлёта (см. рис. 4.) Безопасной скоростью называется скорость, на которой самолёт во взлётной конфигурации обладает удовлетворительной устойчивостью и управляемостью и может перейти к следующему этапу полёта начальному набору высоты L взл раз 4 вув L L, (4.6) где L вув длина воздушного участка взлёта (ВУВ). Траектория ВУВ является криволинейной. В зависимости от типа самолёта и программы полёта вид траектории может быть различным. Однако из-за малой протяжённости этого участка его длину можно определить приближённо, используя закон сохранения энергии, отр L вув Н nxdl. g g 0 Полагая n x = const, получим отр m0g отр Lвув H H. (4.7) nx g Рр Рп g ср Дальнейший требуемый градиент набора высоты должен составлять Рр Рп не менее 3 5 %, т.е. 0,03. 0, 05. m g 4.. Заход на посадку и посадка 0 Заход на посадку начинается с предпосадочного маневрирования самолёта. В соответствии с Авиационными Правилами АП-3, АП-5 [9, 0] заход на посадку должен начинаться не ниже 400 м и заканчиваться на высоте Н пос =5 м (50 ft) над уровнем ВПП. Для небольших самолётов местных воздушных линий (МВЛ) допускается заканчивать заход на посадку на высоте 9 м (30 ft). В процессе этого маневра, который может начинаться с полёта по коробочке на постоянной высоте 400 м с разворотами на 90 0,

43 осуществляется поэтапное изменение конфигурации самолёта от крейсерской к посадочной с постепенным уменьшением скорости полёта до скорости захода на посадку зп. Изменение конфигурации самолёта начинается с выпуска шасси, затем выпускаются предкрылки и в последнюю очередь закрылки (иногда в несколько приёмов). Последний разворот на коробочке предшествует началу снижения самолёта по глиссаде, которая лежит в одной вертикальной плоскости с ВПП. Допускается окончание процесса выпуска закрылков уже на глиссаде (рис. 4.3). Рис Посадка самолёта Посадочной дистанцией называется расстояние, проходимое самолётом по горизонтали, с момента пролёта входной кромки ВПП на высоте Н пос до момента его полной остановки на ВПП (рис. 4.4). = зп H пос = пос Р рев Х а N Y а = 0 F тр L вуп L пр G пос L пос Рис Схема собственно посадки 43

44 Скорость захода на посадку зп, 3св, где св скорость сваливания в посадочной конфигурации. Последнюю находим из условия Y = m пос g или св mпосg с mx S mпосg св ; c S mx зп mпосg,3 ; c S mx пос mпосg c S пос. (4.8) где с у mx максимальный коэффициент подъёмной силы самолёта в посадочной конфигурации; с у пос = 0,85 с у mx ; m пос = m 0 к Т m Т посадочная масса самолёта; к Т коэффициент, зависящий от дальности полёта самолёта 0, если дальность дo 000 км; к Т 0, 3, если дальность от 000 дo 3000 км; 0,7, если дальность свыше 3000 км. На воздушном участке посадки (ВУП) за счёт дросселирования двигателей и постепенного увеличения угла атаки происходит выравнивание траектории, сопровождаемое торможением самолёта с зп до пос и одновременным его снижением до касания ВПП. Длина ВУП рассчитывается энергетическим методом зп пос L вуп кпос H пос, (4.9) g где к пос среднее аэродинамическое качество на ВУП, скорости определяются из выражений (4.8). При пробеге на самолёт действуют те же силы, что и при разбеге. Разница в том, что тяга двигателей отсутствует или направлена назад (реверс), колёса заторможены, используется тормозной парашют. Уравнение движения примет вид m пос d dt Р рев с хпр S f тр. пр m пос g c упр S, (4.0) где f тр.пр = 0, 0,3 коэффициент трения заторможенных колёс по сухому бетонному покрытию. Из (4.0) получим L пр 0 d d g dt 0 пос пос P m рев пос g f тр. пр c d хпр f тр. пр с упр S m пос ; g 44

45 где а пр и b пр постоянные. P рев а пр fтр. пр mпосg 0 d L пр, g а b пос ; b c f с пр пр пр хпр S m тр. пр упр. посg Последний интеграл является табличным. Взяв его, приходим к выражению L пр апр ln. (4.) gb а b пр пр пр пос Посадочная дистанция L пос L L. (4.) вуп Потребная длина ВПП L ВППпотр должна быть не менее:,67 L пос для основных аэродромов;,43 L пос для запасных аэродромов Прерванный и продолженный взлёт При расчёте взлётных характеристик многодвигательных самолётов, кроме нормального взлёта дополнительно рассматривают ещё два варианта взлёта: продолженный взлёт и прерванный взлёт. Оба эти варианта относятся к случаю отказа одного (критического) двигателя. При продолженном взлёте последний продолжается с одним отказавшим двигателем. Дистанцию продолженного взлёта рассчитывают по формуле L взл. прод Lраз, nдв пр nдв Р, отк Lраз Р, отк отр Lвув, (4.3) где L раз длина разбега при всех работающих двигателях от точки старта ( = 0) до скорости отк, при которой происходит отказ критического двигателя. Длина этого участка определяется по формуле, аналогичной (4.4), где вместо отр стоит отк, т.е. L раз а раз ln. (4.4) gb а b раз Длина участка L раз также рассчитывается по формуле, аналогичной (4.4), но в ней уже учитывается отказ критического двигателя и резкое уменьшение тяги на этом участке, скорость изменяется отк до отр. раз раз отк 45

46 где L nдв P n f раз дв а раз тр. раз m0g раз отк отр а раз bраз ln, (4.5) gb а b раз раз ; n дв количество двигателей, создающих продольную тягу при взлёте самолёта. Длину воздушного участка L вув рассчитываем по формуле, аналогичной (4.7), но в ней учтён отказ критического двигателя m 0g отр L вув H. (4.6) n g дв Рр Рп nдв ср nдв Рр Рп nдв Дальнейший требуемый градиент набора высоты m0g должен составлять не менее:, %, если n дв =;,5 %, если n дв = 3;,7 %, если n дв = 4. При прерванном взлёте после отказа критического двигателя пилот производит торможение до полной остановки самолёта. Дистанцию прерванного взлёта рассчитывают по формуле L nдв Р, L 3 Р, отк Lпр, (4.7) взл. прерв Lраз отк раз, nдв где L раз3 длина разбега с одним отказавшим двигателем от момента отказа на скорости отк до момента принятия командиром воздушного судна решения о прекращении взлёта на скорости = отк + t л n x ; t л = 3 с среднее нормативное время реакции пилота; n дв P отк отк c S f тр раз m g сураз S. 0 n храз дв n x продольная перегрузка. m0g m0g m0g а раз bразотк Lраз3 ln. (4.8) gb а b раз раз Длину участка торможения L пр рассчитываем по аналогии с (4.), раз 46

47 где n P L пр дв рев nдв а пр fтр. пр m0g а ln, (4.9) gb а пр пр пр bпр S храз тр. пр ураз. m g ; b c f с пр Существует такая скорость отк, при которой L взл.прод = L взл.прерв. Это сбалансированная скорость отказа EF. Её находят, задаваясь различными значениями отк и рассчитывая L взл.прод и L взл.прерв (рис. 4.5). 0 L взл.прерв L взл.прод L взл L взл.прод L сб L сб L взл.прерв норм. взлёт 0 отк EF 0 EF отк Рис К расчёту сбалансированной скорости отказа EF Величине EF соответствует скорость принятия решения и сбалансированная длина взлётной дистанции L сб. Потребная длина ВПП L ВППпотр (вместе с концевой полосой безопасности (КПБ)) должна быть не менее L сб. 5. МАНЕВРЕННЫЕ ХАРАКТЕРИСТИКИ САМОЛЁТА Способность самолёта изменять свою скорость в полёте как по величине, так и по направлению, определяет его маневренность. Важнейшими показателями маневренности являются предельные значения перегрузок n x, n, n, создаваемые самолётом в полёте, либо время маневра при заданном изменении параметров движения [, 4, 6, 7, ]. В общем случае маневр самолёта является пространственным, однако достаточно полное представление о маневренных возможностях самолёта даёт анализ показателей его маневренности для двух упрощённых вариантов маневрирования маневры только в горизонтальной плоскости и только в вертикальной плоскости. 47

48 5.. Горизонтальная приемистость Способность самолёта изменять скорость горизонтального полёта при разгоне называют горизонтальной приемистостью. Чем меньше время перехода от скорости до скорости, тем выше горизонтальная приемистость. Из первого уравнения системы (.) имеем d g n xа. dt Отсюда время разгона от скорости до скорости где n P P mg xа p п t раз, (5.) g d n. Интеграл в (5.) берётся численно. 5.. Криволинейный полёт в горизонтальной плоскости вираж В этом случае 0, тогда системы уравнений (.5) и (.) примут вид g ; (5.) n xа xа n cos n sin ; (5.3) а а g n а sin nа cos ; (5.4) cos ; (5.5) x g sin. (5.6) g Необходимым условием выполнения криволинейного полёта в горизонтальной плоскости является наличие центростремительной силы, направленной к центру кривизны траектории полёта. Её можно создать креном самолёта, скольжением или одновременным использованием крена и скольжения. Маневр, выполняемый для изменения направления полёта (угла пути Ψ), называется разворотом. Полный разворот на называется виражом. Вираж, при выполнении которого, α, β, γ = const называют установившимся. Правильный вираж (рис. 5.) это установившийся вираж без скольжения (β = 0, n а = 0). Для него уравнения (5.) (5.6) примут вид n xа = 0; (5.7) 48

49 n а ; (5.8) cos g у nа sin. (5.9) Из (5.8) следует, что на вираже нормальная перегрузка всегда больше. вир вир γ Y R вир Ψ ω у =dψ/dt N n γ G Рис. 5.. Маневр правильный вираж Рассчитаем радиус правильного виража вир вир у Rвир Rвир Rвир. Учитывая здесь (5.9), получим Теперь подставим (5.8) в (5.0). В итоге имеем Время выполнения правильного виража вир R вир. (5.0) g n sin а вир вир R вир. (5.) g tg g n а Rвир вир t вир (5.) вир g n Перегрузка в исходном горизонтальном прямолинейном установившемся полёте гп cугп S nуагп. mg а 49

Видео:Что такое перегрузка? - Основы авиации #14Скачать

ОБЩИЕ СВЕДЕНИЯ ПО ДИНАМИКЕ ПОЛЕТА ВС

Динамика полета — это наука о законах движения летательных аппаратов (в данном случае — самолета). Основная задача динамики полета- выявление закона движения самолета под действием заданных сил и моментов (или определение системы сил и моментов, необходимой для реализации заданного закона движения). Другой весьма важной задачей динамики полета является определение закона движения самолета, обеспечивающего экстремальное (максимальное или минимальное) значение какого-либо параметра (максимальной дальности полета, минимального времени выхода заданную точку и т. п.). При изучении Курс основ динамики полета обычно делят на два раздела. В первом разделе изучают законы движения центра тяжести самолета, т. е. законы движения самолета как материальной точки. В этом случае силы, действующие на самолет, приложены в центре тяжести его, а моменты внешних сил уравновешены. Во втором разделе рассматривают движение самолета как твердого тела. При этом изучают общий случай движения тела с учетом, как перемещения центра тяжести, так и вращения относительно его под действием моментов внешних сил. В этом разделе исследуют моменты, приложенные к самолету, и характер движения его. Основные положения динамики полета самолета как науки были разработаны в работах Н. Е. Жуковского по аэродинамике и авиации. В работе «О парении птиц»(1891 г.) он анализирует условия выполнения полета и различные траектории движения при различных положениях центра тяжести. Среди рассмотренных траекторий была траектория вида «мертвой петли». Практические выводы, сделанные Н. Е. Жуковским, подтвердил П. Н. Нестеров, впервые в мире совершивший петлю в вертикальной плоскости («петля Нестерова»). В разработке методов расчета неустановившихся движений самолета большое значение имели работы одного из учеников Н. Е. Жуковского В. П. Ветчинкина «Динамика полета самолета» (1933 г.), а также В. С. Пышнова, А. Н. Журавченко, Б. Т. Горощенко и других советских ученых. Решению проблем динамики переменной массы посвящены труды К. Э. Циолковского и И. В. Мещерского.

СИЛЫ, ДЕЙСТВУЮЩИЕ НА САМОЛЕТ В ПОЛЕТЕ.ВИДЫ ДВИЖЕНИЯ САМОЛЕТА

Величина и направление скорости движения самолета зависят от величины и направления внешних сил, действующих на него. Эти силы являются результатом воздействия на самолет воздушной среды, массы воздуха, отбрасываемой двигателем, и массы Земли. В результате взаимодействия самолета с воздушной средой появляются аэродинамические силы. Воздух, отбрасываемый двигателем, вызывает появление силы тяги. Сила веса самолета есть результат действия на него массы Земли.

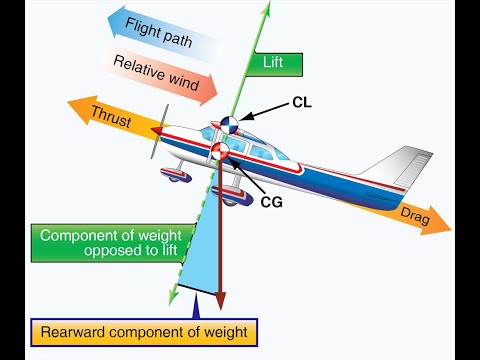
Таким образом, на летящий самолет действуют силы веса G, аэродинамическая R и тяги Р двигателя (см. рисунок ниже). Сила веса G приложена в центре тяжести самолета и направлена по радиусу к центру тяжести Земли. Аэродинамическая сила R приложена в центре давления. В общем случае она может быть заменена тремя составляющими: подъемной силой Y, силой лобового сопротивления К и боковой силой Z. Сила Y направлена перпендикулярно к вектору скорости, сила X — по касательной к траектории движения, а боковая сила Z — по нормали к плоскости сил Y и X. Силы Y и X лежат в плоскости симметрии самолета.

Сила тяги двигателя Р, как правило, действует в плоскости симметрии самолета. Она может иметь две составляющие: Рх — проекция на касательную к траектории движения и Ру — проекция на нормаль к траектории (см.рисунок ниже).

Ввиду малого значения составляющей Ру принимают, что сила тяги Р направлена по касательной к траектории движения самолета.

В первом разделе динамики полета принимают моменты всех сил относительно центра тяжести самолета уравновешенными. Поэтому все внешние силы можно приложить в центре тяжести самолета. В дальнейшем будут рассмотрены различные виды движений самолета под действием внешних сил R, Р и G, приложенных в его центре тяжести. Все силы, направленные параллельно вектору скорости, называются продольными, а перпендикулярно к вектору скорости — поперечными. Сила веса G может быть или продольной (отвесное пикирование), или поперечной (горизонтальный полет),или иметь продольные и поперечные составляющие (планирование, подъем самолета). Сила тяги может тоже иметь как продольную, так и поперечную составляющую (Рх и Ру).В каждый момент самолет при движении имеет вполне определенные величину и направление скорости. Если направление скорости со временем не изменяется, то полет самолета будет прямолинейным, в противном случае — криволинейным. Если при этом сохраняется величина скорости, то движение самолета будет равномерным. При увеличении скорости движение самолета будет ускоренным, при уменьшении — замедленным. Движение самолета с положительным ускорением называется разгоном, а с отрицательным ускорением — торможением. Следует заметить, что величина и направление скорости еще не дают полной характеристики полета. Поэтому чаще полет самолета характеризуется понятием «режим полета». Под режимом полета самолета понимают не только величину и направление скорости, но и высоту полета, характер траектории, ускорение и другие параметры движения. Ранее указывалось, что вид движения самолета определяется величиной и направлением равнодействующих продольных и поперечных сил. Если равнодействующая продольных сил направлена вперед, то движение самолета ускоренное. Сама сила является ускоряющей. Если эта сила направлена назад, то движение самолета будет замедленным (торможение) Таким образом, продольные силы влияют на изменение величины скорости движения самолета

Так как равнодействующая поперечных сил R направлена вдоль радиуса кривизны траектории, то она является центростремительной силой. Эта сила искривляет траекторию движения в сторону своего действия. Векторы скорости V и поперечной силы Rп могут лежать в одной плоскости (плоскость криволинейного

движения) и в разных плоскостях. В последнем случае траектория движения будет пространственной (спираль, боевой разворот и другие виды движения).

УРАВНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА ТЯЖЕСТИ САМОЛЕТА

Из механики известно, что движение свободного тела в пространстве можно представить состоящим из поступательного движения его центра тяжести и вращения тела относительно центра тяжести. В первом разделе динамики самолета рассматривается только движение центра тяжести. Поэтому уравнения, связывающие внешние силы с ускорениями, которые они сообщают самолету, составляются только для движения его центра тяжести (центра масс). Эти уравнения назвали уравнениями движения центра тяжести самолета. Они используются для определения количественных характеристик полета самолета и их качественного анализа.

Любое движение центра тяжести самолета можно разложить на движения его по трем взаимно перпендикулярным осям. Так как движение самолета рассматривается относительно воздушной среды, то уравнения движения центра тяжести изучаются относительно так называемой поточной или скоростной системы координат. За начало координат в этой системе принимают центр тяжести самолета (точка О). Ось Ох направляют по вектору скорости (по касательной к траектории движения). Ось Оу располагают в вертикальной плоскости перпендикулярно к вектору скорости, а ось Oz — перпендикулярно к плоскости хОу. Положительное направление осей показано на рисунке.

Система координат подвижная, перемещается вместе с самолетом, однако система не позволяет построить траекторию движения, а отражает лишь связь ускорения с внешними силами. При рассмотрении вопросов, связанных с вращением самолета относительно его центра тяжести, удобнее пользоваться так называемой связанной системой координат. Эта система позволяет любое вращательное движение заменить вращением относительно трех взаимно перпендикулярных осей, проходящих через центр тяжести (см. рисунок):

— продольная ось самолета Ох, расположенная в плоскости симметрии самолета параллельно корневой (центральной) хорде крыла;

— путевая, или вертикальная, ось самолета Оу, расположенная в плоскости симметрии самолета и перпендикулярная к продольной оси;

— поперечная ось самолета Oz, перпендикулярная к плоскости хОу.

Моменты внешних сил относительно оси Ох называются поперечными Мх, относительно оси Оz – путевыми Му и относительно оси Oz — продольными Mz.

Угол γ у поворота самолета относительно оси Ох называется углом крена. Угол β поворота самолета относительно оси Оу называется углом рыскания. И, наконец, угол поворота самолета относительно оси Oz называется углом атаки. Положительное направление вращения определяется по правилу «буравчика», ввинчиваемого по положительному направлению той или иной оси (по направлению движения часовой стрелки). Связанная система координат используется при изучении вопросов балансировки, устойчивости и управляемости самолета. Выразим уравнения движения центра тяжести самолета в скоростной (поточной) системе координат. Обозначим проекции равнодействующей внешних сил на оси координат соответственно через Fx, Fy и, проекции ускорений — через j_i, j_y и j_z и массу самолета через m_{с-та .} Тогда второе уравнение механики F= m_с-та j проекциях на оси координат выразится в следующем виде:

Ускорение , направленное по касательной к траектории движения, называют тангенциальным или продольным. Оно характеризует только изменение величины скорости. При > 0 происходит разгон самолета, при Х), или замедленным (Р 2 ,

r — радиус кривизны траектории, м.

Предыдущее равенство можно преобразовать в следующее:

,

Из этой формулы следует, что при больших скоростях в горизонтальном полете подъемная сила меньше веса самолета. При скорости V = подъемная сила горизонтального полета равна нулю. Эта скорость получила название первой космической скорости. Самолет в данном случае будет двигаться по траектории искусственного спутника Земли. Первая космическая скорость для земных условий составляет 7900 м/сек. Если полет самолета происходит с небольшими скоростями, подъемная сила мало отличается от веса самолета. Так, например, при скорости полета V = 2500 км/час подъемная сила меньше веса самолета всего на 1%. Это позволяет при анализе горизонтального полета современных самолетов считать, что Y=G.

Потребная скорость горизонтального полета

При горизонтальном полете на данном угле атаки должно быть выполнено равенство Y=G. Известно, что каждому углу атаки соответствует вполне определенное значение c_y. Для обеспечения равенства Y = G данному углу атаки должна соответствовать и вполне определенная величина скорости на заданной высоте полета. Скорость полета, необходимая для создания подъемной силы, равной весу самолета на данном угле атаки, называется п о т р е б н о й с к о р о с т ь ю г о р и з о н т а л ь н о г о п о л е т а.

Потребная скорость горизонтального полета зависит от угла атаки полета, т. е. с_у, от высоты полета, т. е. , и от удельной нагрузки на крыло . С ростом углов атаки до α = α_кр увеличивается коэффициент с_у. Потребная скорость горизонтального полета при этом уменьшается. На критическом угле атаки, при котором c_у = c_уmax потребная скорость горизонтального полета достигает минимального значения. Эта скорость получила название м и н и м а л ь н о т е о р е т и ч е с к о й .

Практически полет на критических углах атаки не производится. При полете на α = α_кр из-за сильного срыва воздушного потока с крыла, возможно сваливание самолета на крыло или на нос. Приближение к критическому углу атаки обнаруживается в полете по тряске самолета. После начала тряски угол атаки увеличивать опасно.

С целью обеспечения безопасности полета наибольшая допустимая величина с_у должна быть меньше c_уmax. Скорость полета, когда коэффициент подъемной силы c_у равен коэффициенту подъемной силы при тряске c_{у доп} называется м и н и м а л ь н о д о п у с т и м о й.

За минимально допустимую скорость иногда принимают так называемую с к о р о с т ь с в а л и в а н и я или с р ы в а . Скорость, при которой происходит непроизвольное сваливание самолета на крыло или на нос, называется скоростью сваливания или скоростью срыва.

Так же, чем больше удельная нагрузка на крыло, тем больше потребная скорость горизонтального полета. У современных самолетов несущие способности крыльев малые, а удельные нагрузки на крыло повышенные (500-600 кГ/м 2 ). Поэтому потребные минимальные скорости горизонтального полета их имеют большое значение (200-300 км/час). С подъемом на высоту из-за

уменьшения массовой плотности воздуха ρ потребная скорость горизонтального полета увеличивается.

Потребная тяга горизонтального полета

Из условия постоянства скорости в горизонтальном полете следует, что должно быть равенство силы тяги Р и силы лобового сопротивления X.

Тяга, необходимая для уравновешивания лобового сопротивления самолета при полете на данной скорости (угле атаки), называется п о т р е б н о й т я г о й г о р и з о н т а л ь н о г о п о л е т а Р_г.п..

Выясним факторы, влияющие на потребную тягу горизонтального полета. Каждому углу атаки полета соответствует вполне определенное аэродинамическое качество самолета.

Максимальное качество самолета соответствует наивыгоднейшему углу атаки. На этом угле атаки потребная тяга минимальна. На меньших и больших углах атаки потребная тяга будет больше. Так как каждому углу атаки соответствует определенная скорость (число М), то потребная тяга зависит от скорости (числа М) полета.

Разберем характер зависимости потребной тяги горизонтального полета от скорости для определенного веса самолета и высоты полета. С ростом скорости полета угол атаки становится меньше. Качество самолета до α = α_наив увеличивается, а на больших углах атаки уменьшается. Поэтому потребная тяга с ростом скорости, до скорости, соответствующей α = α_наив уменьшается, а при больших скоростях увеличивается. На рисунке представлен график, показывающий зависимость потребной тяги горизонтального полета от скорости, который назвали кривой Жуковского. Потребная тяга горизонтального полета зависит так­же от веса самолета и высоты полета. При полете на данном угле атаки с ростом веса самолета потребная тяга увеличивается.

Физически это означает, что для горизонтального полета более тяжелого самолета требуется большая подъемная сила. Это достигается увеличением потребной скорости. При увеличении последней растет сила лобового сопротивления X и как результат потребная тяга горизонтального полета. Это приводит к смещению всех точек кривой потребной тяги в сторону больших скоростей и тяг.

С увеличением высоты при постоянном угле атаки потребная скорость горизонтального полета увеличивается, а потребная тяга остается постоянной.

С подъемом на высоту вследствие уменьшения скорости звука увеличивается число М. Оно может оказаться больше М_кр. При полетах на М > М_кр возникает волновой кризис, появляется волновое сопротивление. Аэродинамическое качество самолета при том же су будет уменьшаться. Это приводит к интенсивному росту потребной тяги на V > V_кр.

ВЗЛЕТ И ПОСАДКА

Динамика полета как раздел аэромеханики рассматривает вопросы, связанные с реализацией различных траекторий полета самолета, которые определяются техническим заданием на проектирование. Для самолетов различного назначения различна и так называемая номенклатура режимов полета, однако для всех самолетов общими являются режимы взлета и посадки.

Взлет — это ускоренное движение самолета с момента страгивания на линии старта до момента одновременного достижения регламентируемых в техническом задании высоты и безопасной скорости взлета, обеспечивающих безопасность полета на участке начального набора высоты.

В конце разбега самолет достигает скорости отрыва, при которой можно безопасно оторвать самолет от земли и продолжать взлет. На высоте Н = 400 м уже должны быть убраны шасси, взлетно-посадочная механизация, двигатели переведены на режим крейсерского полета и самолет начинает полет по маршруту.

Взлет самолета состоит из следующих этапов: разбега, отрыва и разгона с подъемом.

Разбегом самолета называется ускоренное движение его по земле (воде), необходимое для набора скорости, при которой происходит безопасный отрыв. Разбег является равноускоренным движением самолета.

Минимальная скорость безопасного отделения самолета от земли (воды) называется скоростью отрыва.

Разгон с подъемом есть ускоренный прямолинейный полет с малым углом подъема до безопасной высоты 25 м.

Момент отделения самолета от земли (воды) называют отрывом

Расстояние от начала разбега до набора высоты 25 м называется взлетной дистанцией.

Расстояние от начала разбега до отрыва называется длиной разбега. Она определяет длину взлетно-посадочной полосы.

Основными характеристиками взлета являются

· длина взлетной дистанции.

На самолет при разбеге действуют сила веса G, аэродинамические силы X и Y, тяга силовой установки Р.

📹 Видео

Основы динамики самолета, крен, тангаж и рысканье - Основы Авиации #3Скачать

Аэродинамика для всех - Часть 8 Горизонтальный полёт Кривые ЖуковскогоСкачать

Как летает самолет? Закон Бернулли - Основы авиации #2Скачать

Принципы обеспечения устойчивости и управляемости. Авиамодельный цикл 3. Простейшие авиамодели.Скачать

Аэродинамика для всеx - Часть 3 Центровка, Органы управленияСкачать

Подъёмная сила крыла ● 1Скачать

Аэродинамика для всех - Часть 2 Закон Бернулли, Угол атакиСкачать

Причины и виды перегрузокСкачать

Урок 93. Основное уравнение динамики вращательного движенияСкачать

Урок 63. Перегрузка. Вес тела на полюсе и на экватореСкачать

Лекция 2 | Динамика полетаСкачать

АУПО. Силы и моменты, действующие на летательный аппарат. Математическая модель.Скачать

3-2 Численное моделирование полёта ракетыСкачать

Урок 135. Применения ур-ния Бернулли (ч.2). Подъемная сила крыла самолета (ч.1)Скачать

Лекция 1 | Динамика полетаСкачать

Урок 136. Подъемная сила крыла самолета (часть 2)Скачать

Лекция 2 Динамика полета самолета. Часть 3 Взлет самолетаСкачать

Лекция 2 Динамика полета самолета. Часть 5 Пилотаж самолетаСкачать