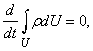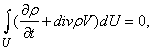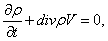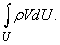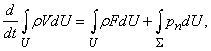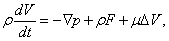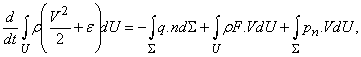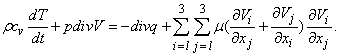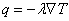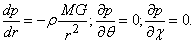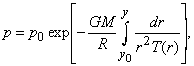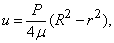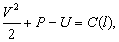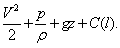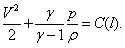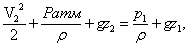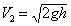Уравнения движения и равновесия идеальной несжимаемой жидкости в однородном поле силы тяготения (7 видео)

ГИДРОАЭРОМЕХАНИКА

ГИДРОАЭРОМЕХАНИКА – наука о движении и равновесии жидкостей и газов. При планировании физических экспериментов или при их проведении необходимо создавать теоретические модели, которые либо предсказывают возможные результаты этих экспериментов, либо объясняют уже полученные. Только в тесном взаимодействии теории и эксперимента можно понять то, что происходит в окружающем нас физическом мире. Для создания той или иной количественной или качественной модели физического явления необходим математический фундамент, на основе которого строятся такие модели. Под математическим фундаментом в данном случае подразумеваются те дифференциальные уравнения и те граничные и начальные условия, с помощью которых можно было бы описывать рассматриваемое физическое явление. Гидромеханика и предлагает модели и аппарат для иcследования явлений, происходящих в жидкостях и газах.

Содержание

О гипотезе сплошности среды.
Замкнутая система уравнений гидроаэромеханики.
Гидростатика
Равновесие совершенного газа в поле сил тяжести.
Течения идеальных жидкостей и газов.
Интеграл Бернулли.
Ударные волны как одно из важных проявлений сжимаемости газа.
Лекция 2
Автор —
ЛЕКЦИЯ №2. Однородная несжимаемая жидкость
💡 Видео

Видео:Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

О гипотезе сплошности среды.

Гидроаэромеханика изучает движения жидкостей и газов в приближении, когда они могут рассматриваться как сплошные среды, т.е. среды, непрерывным образом заполняющие рассматриваемое пространство течения. Чтобы решать математические проблемы, связанные с расчетом движения различных объектов (самолетов, ракет, кораблей и др.) в воздухе или воде, с изучением волновых процессов в жидкостях и газах, с их течениями по трубам и каналам и т.п., необходим математический аппарат, описывающий эти явления. Этим аппаратом и являются уравнения гидроаэромеханики, которые опираются на гипотезу сплошности среды, т.е. на гипотезу о том, что частицы жидкости или газа непрерывным образом заполняют занимаемую ими часть физического пространства.

Возникает естественный вопрос: при каких предположениях справедлива эта гипотеза? Если для жидкостей (воды, жидких металлов и т.п.) эта гипотеза более или менее очевидна, то для достаточно разреженных газов (например, занимающих космическое пространство, включая атмосферы звезд, планет и Солнца), которые состоят из отдельных атомов или молекул, а также других физических объектов, к которым применим аппарат гидроаэромеханики, она требует своего обоснования. Так, например, при расчете торможения искусственных спутников Земли использование математического аппарата гидроаэромеханики не представляется возможным, в то время как именно этот аппарат используется при расчете торможения космических объектов, входящих в плотные слои атмосфер Земли и планет (например, метеоритов или возвращаемых на Землю космических кораблей и пр.). На этот вопрос легко ответить при выводе уравнений. Однако из этого вывода следует, что гипотеза сплошности среды справедлива, в частности, в том случае, когда характерный размер обтекаемого тела L (например, радиус сферического спутника) много больше длины свободного пробега атомов или молекул газа l, т.е. длины между последовательными их столкновениями.

Видео:Вывод уравнений движения идеальной жидкости - Лекция 2Скачать

Замкнутая система уравнений гидроаэромеханики.

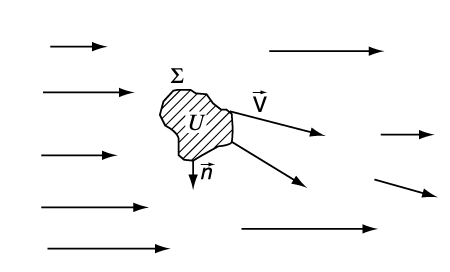
Уравнения гидроаэромеханики в их упрощенном виде представляют собой сложную систему нелинейных дифференциальных уравнений для массовой плотности r (масса жидкости или газа в единице объема), вектора скорости V и давления p, которые, в свою очередь, являются функциями пространственных координат (например, x, y и z в декартовой системе координат) и времени t. Не вдаваясь в математические подробности вывода этих уравнений, можно рассмотреть основные идеи этого вывода, тем более, что эти уравнения представляют собой известные даже из школьных учебников законы сохранения массы, импульса и энергии. Для этого рассматривается некоторый физический объем, непрерывным образом заполненный жидкостью или газом. На рис. 1 изображена движущаяся жидкость (или газ), непрерывным образом заполняющая некоторую часть физического пространства. Выделим из нее некоторый объем U (ограниченный поверхностью S), который в течение всего времени движения состоит из одних и тех же частиц жидкости (этот объем заштрихован).

Очевидно, что при своем движении масса жидкости, заключенная в объеме U, остается постоянной (если, конечно, нет каких-либо дополнительных источников этой массы), хотя сам объем может сильно деформироваться, поскольку частицы не скреплены жестко, как в твердом теле. Если выделить из рассматриваемого объема бесконечно малый элемент DU, то очевидно, что в этом элементе масса жидкости или газа будет равна rDU. Тогда закон сохранения массы, заключенной в выделенном объеме U, можно записать в виде

т.е. масса жидкости или газа, заключенная в выделенном объеме U, не изменяется со временем. Здесь интеграл берется по выделенному объему U, который меняется со временем t. Если использовать формулу производной по времени от интеграла по движущемуся объему, можно получить уравнение

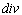
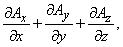
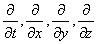
где оператор дивиргенции , примененный к произвольному вектору А, в декартовой системе координат будет имеет вид

а – частные производные по времени t и координатам x, y, z соответственно.

Закон сохранения массы в интегральной форме справедлив как для непрерывных, так и для разрывных функций r и V. Для непрерывных функций закон сохранения массы можно записать в дифференциальной форме

Это уравнение в гидроаэромеханике обычно называется уравнением неразрывности.

Аналогично можно записать теперь закон сохранения импульса. Импульс единицы объема жидкости, равен rV, в элементарном объеме rDU, а в выделенном объеме U –

Обобщение второго закона Ньютона на жидкие среды заключается в том, что кроме массовых сил (например, силы гравитации), которые действуют на любую частицу жидкости, находящуюся внутри выделенного объема U, действуют еще поверхностные силы, которые возникают от воздействия частиц жидкости, примыкающих к поверхности S с внешней от выделенного объема U стороне. Тогда закон сохранения импульса имеет вид

где p_n– вектор поверхностной силы, который действует на элемент поверхности S с единичным вектором нормали n. Одной из основных проблем гидроаэромеханики, окончательно решенной в середине 19 в., является явное определение поверхностных сил. В рамках используемого здесь так называемого феноменологического подхода к получению уравнений гидроаэромеханики, поверхностные силы определяются эмпирически. Дифференцируя по времени интеграл слева в уравнении импульса, как это делалось при выводе уравнения неразрывности, и переходя от поверхностного интеграла справа к объемному, можно написать дифференциальные уравнения движения для непрерывных функций в виде

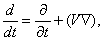
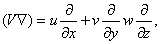
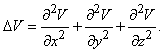
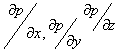
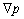
а величины u, v и w, а также – являются проекциями векторов скорости V и градиента давления на оси Ox, Oy и Oz соответственно.

Это уравнение, называемое уравнением Навье – Стокса, выписано в наиболее простой форме для несжимаемой жидкости, где поверхностные силы сводятся к нормальному давлению р, а последний член справа представляет собой «вязкие» силы (m – коэффициент вязкости) в предположении, что r = const.

Впервые уравнение движения было выведено в середине 18 в. Л.Эйлером, когда он работал в Петербургской Академии наук. Поскольку эффекты вязкости в жидкости в то время еще не были известны, то Эйлер получил это уравнение при m = 0. В честь его эти уравнения были названы уравнениями Эйлера. Только в 1822 французским инженером Навье в уравнения Эйлера были введены силы, связанные с вязкостью, определяемой коэффициентом m. В общей форме, справедливой и для сжимаемого газа, уравнение получено Стоксом и получило название уравнения Навье – Стокса.

Для несжимаемой жидкости дифференциальные уравнения неразрывности и импульса (одно скалярное и одно векторное) являются замкнутой системой уравнений для определения вектора скорости V и скалярного давления р (r = const). Если же r № const, то требуется дополнительное уравнение. Это уравнение получается из закона сохранения энергии.

Обобщение закона сохранения энергии на случай движения жидкостей и газов получается аналогично обобщению второго закона Ньютона, однако, в силу наличия теплового движения в жидкостях и газах, энергия, приходящаяся на единицу объема, состоит из кинетической энергии rV 2 /2 и внутренней энергией re, связанной с тепловым движением частиц газа или жидкости. Полная энергия в элементе объема DU равна r(V 2 /2 + e)DU.

Изменение полной энергии в выделенном объеме U равно притоку тепла через поверхность S за счет теплопроводности, а также работе массовых и поверхностных сил, т.е. вместо закона сохранения импульса, получается уравнение

где n – единичный вектор нормали к поверхности S.

Для совершенного газа e = c_v T, где с_v – теплоемкость при постоянном объеме, T – температура, а для вектора потока тепла обычно принимается эмпирический закон Фурье q = – l 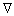T (l – коэффициент теплопроводности). После соответствующего дифференцирования по времени левой части уравнения энергии, перехода от поверхностных интегралов к объемным и при использовании уравнения неразрывности и уравнения движения, можно получить так называемое уравнение притока тепла для непрерывных функций

Все эти уравнения, вместе с уравнением состояния для совершенного газа

где R = (с_р – с_v ) – газовая постоянная, а с_р – теплоемкость при постоянном давлении, и законом Фурье

Образуют замкнутую систему уравнений гидроаэромеханики для определения вектора скорости V, давления p, плотности r и температуры Т.

Если какое либо физическое явление мало зависит от диссипативных процессов (вязкости и теплопроводности), то уравнения эти уравнения сводятся к уравнениям гидроаэромеханики идеальной жидкости. В этом случае замкнутой системой уравнений для определения р, r, V и Т является система

Последнее уравнение есть адиабатический закон, который легко сводится к закону сохранения энтропии. Здесь g = с_p/c_v – показатель адиабаты, т.е. отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме.

Видео:14. Движение идеальной жидкостиСкачать

Гидростатика

представляет собой частный случай гидроаэромеханики, который изучает равновесие жидкостей и газов, т.е. их состояние при отсутствии гидродинамической скорости (V = 0). Результаты и методы гидростатики имеют большое значение для многих задач, важных как с практической, так и с общенаучной точек зрения. В гидростатике рассматриваются задачи, связанные с равновесием воды в водных бассейнах, воздуха в атмосфере Земли, решаются задачи расчета сил, которые действуют на тела, погруженные в жидкость или газ, определяются распределения давления, плотности, температуры в атмосферах планет, звезд, Солнца и множество других задач.

Уравнения гидростатики получаются из уравнений гидроаэромеханики при V = 0. В частности, уравнения сохранения импульса дает

Откуда, в частности, следует известный еще из школьных учебников закон Паскаля, согласно которому при отсутствии внешних массовых сил (F = 0) давление всюду является постоянным (p = const ).

Видео:Уравнение движенияСкачать

Равновесие совершенного газа в поле сил тяжести.

Пусть есть газ в центральном поле сил тяжести. Уравнения равновесия в сферической системе координат будут в этом случае записываются как:

Здесь r, q и c – соответственно расстояние до притягивающего центра массы М, помещенного в начало координат, угол, отсчитываемый от полярной оси Оz, и угол в плоскости Оxy, G – гравитационная постоянная, равная 6,67Ч10 –8 дин см 2 г –2 .

Из этих уравнений видно, что в центрально-симметричном поле гравитации давление зависит только от расстояния до этого центра (легко показать, что давление не зависит и от времени). Легко также показать, что плотность и температура также зависят только от координаты r. Интегрирование первого из этих уравнений приводит к так называемой барометрической формуле, если под М понимать массу Земли, планеты, звезды, Солнца и др. При использовании уравнения состояния барометрическая формула имеет вид

где p₀ – давление на некотором расстоянии r = r₀ от притягивающего центра (для Земли, например, это может быть давление на уровне моря). Эта формула определяет распределение давления в атмосферах звезд, Земли, планет, Солнца и др., если известно распределение температуры Т(r), однако эту температуру часто нельзя определить из написанного ранее уравнения притока тепла, так как в нем учитывается только приток тепла за счет теплопроводности, в то время как для перечисленных атмосфер есть другие источники тепла, неучтенные в приведенном уравнении. Например, атмосфера Солнца разогревается различного рода волновыми процессами, а атмосфера Земли перерабатывает энергию солнечного излучения и т.п., поэтому для определения распределения давления в атмосферах небесных тел при помощи барометрической формулы часто используются эмпирические зависимости Т(r).

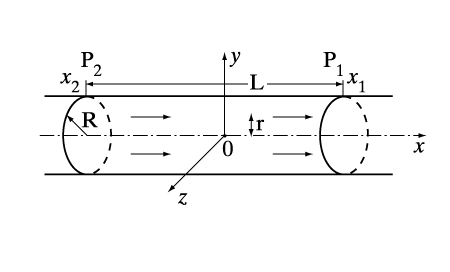
Можно, например, рассчитать распределения давления в атмосфере Земли до расстояний в 11 км от ее поверхности. Если выбрать декартову систему координат с началом на поверхности Земли и направить ось Oz вертикально вверх, тогда в барометрической формуле вместо координаты r нужно брать координату z = r – R_Е, где R_Е – радиус Земли. Поскольку этот радиус много больше толщины атмосферы (z p₁), не влияют на течение в большей части этой трубы, то легко получить точное аналитическое решение уравнения Навье – Стокса в виде

где u – скорость жидкости вдоль оси х, совпадающей с осью симметрии трубы, а r – расстояние от этой оси. Из этой видно, что профиль скорости в трубе является параболическим. На стенках трубы скорость обращается в нуль вследствие прилипания жидкости из-за эффекта вязкости. Такое течение было изучено в середине 19 в. Пуазейлем и Гагеном на примере течений жидкостей в капиллярах и получило название течения Гагена – Пуазейля.

Очевидно, при постоянном потоке (не зависящем от r) жидкости у входа в трубу и на ее начальном участке профиль скорости не будет совпадать с приведенным решением. Параболический профиль устанавливается лишь на достаточно большом расстоянии от входного участка, именно поэтому для получения решения нужно предположить, что труба достаточно длинная, при этом для таких труб это точное решение хорошо совпадает с экспериментальными данными.

Полученное решение описывает стационарное, гладко-слоистое течение, которое обычно называют ламинарным. Однако из практики известно, что в трубах иногда течение бывает нестационарным, с пульсациями скорости, с перемешиванием между слоями, это течение обычно называется турбулентным. Опыты Рейнольдса, проведенные в 1883, показали, что при достаточно больших значениях числа r U L/m, где U – средняя по сечению трубы скорость жидкости, параболический профиль становится неустойчивым по отношению к малым возмущениям, а при дальнейшем увеличении этого числа течение в трубе становится турбулентным. Это число получило название числа Рейнольдса (Re), которое играет очень важную роль в различных задачах гидроаэромеханики. В частности оно характеризует отношение инерционных сил (левая часть уравнения) к силам вязкости, при этом часто силами вязкости можно пренебречь и использовать уравнения гидроаэромеханики идеальной жидкоститолько при Re >> 1.

Видео:Теорема Эйлера о движении жидкостиСкачать

Течения идеальных жидкостей и газов.

Часто важные в приложениях задачи рассматривают на основе уравнений гидроаэромеханики идеальной жидкости, а не на полных уравнениях. Это связано с тем, что математически уравнения идеальной гидроаэромеханики существенно проще. Если нужно определить подъемную силу крыла самолета при малых дозвуковых скоростях, то вязкие силы пренебрежимо малы и нет необходимости использовать уравнения Навье – Стокса. Однако для определения сопротивления такого крыла при движении его в воздухе вязкие силы оказываются определяющими и необходимо использовать более сложный математический аппарат, связанный с уравнениями Навье – Стокса.

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Интеграл Бернулли.

При некоторых предположениях уравнения гидромеханики идеальной жидкости можно один раз проинтегрировать, они имеют решения, одним из которых является интеграл Бернулли для стационарных течений (по имени современника Эйлера математика Бернулли, впервые получившего этот интеграл)

где P (p) = т dp/r(p) – функция давления, U – потенциал внешних массовых сил, С – постоянная вдоль линии тока l (линия тока совпадает с вектором скорости течения V). Так, например, для несжимаемой жидкости в поле земного тяготения это уравнение имеет вид

Для адиабатических течений интеграл Бернулли в отсутствии внешних массовых сил имеет вид

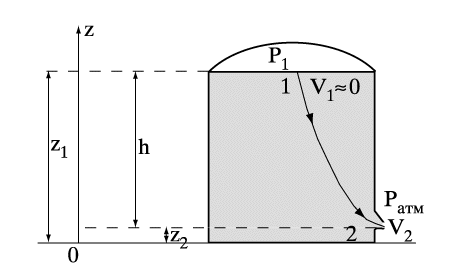
В качестве примера использования интеграла Бернулли можно определить скорость истечения несжимаемой жидкости из сосуда (рис. 5). При истечении жидкости из этого сосуда уровень жидкости понижается, т.е. скорость поверхности жидкости, вообще говоря, отлична от нуля. Однако при достаточно широком сосуде с узким отверстием вытекания можно принять, что V₁ » 0. Поскольку по всей поверхности жидкости в сосуде давление р₁ = const, то постоянная вдоль линии тока на всех линиях тока будет одинаковой. Интеграл Бернулли вдоль какой-нибудь линии тока, например, соединяющей точки 1 (на поверхности) и 2 (у выходного отверстия)

где р_атм – атмосферное давление у выходного отверстия. Отсюда легко получить формулу для скорости истечения V₂. В частном случае р_атм = р₁ получаем так называемую формулу Торичелли для истечения жидкости из широкого сосуда с узким выходным отверстием

по имени итальянского ученого Э.Торричелли (1608–1647). Здесь h = (z₁ – z₂ ). Для ванны с высотой налитой воды примерно 0,5 м скорость истечения V₂ » 3,1м/сек.

Уравнения движения идеальной жидкости имеют еще один интеграл для нестационарных течений, который называется интегралом Коши – Лагранжа. Он справедлив для течений, в которых отсутствуют вихри. Его часто, например, используют при рассмотрении волновых движений жидкости или газа.

Видео:Леонтьев Н.Е. - Основы механики сплошных сред. Семинары - 6. Уравнение баланса импульсаСкачать

Ударные волны как одно из важных проявлений сжимаемости газа.

Математически уравнения идеальной гидроаэромеханики допускают разрывные решения, т.е. решения, которые имеют скачки параметров газа (плотности, давления, скорости и температуры). Одним из таких проявлений в природе является образование ударной волны около летящего со сверхзвуковой скоростью тела в плотных слоях атмосферы Земли. Например, образование ударной волны около летающих сверхзвуковых самолетов или ударных волн около метеоритов, вторгающихся в плотные слои атмосферы Земли с большими сверхзвуковыми скоростями. В условиях космического пространства хорошо известны межпланетные ударные волны, которые чаще всего являются результатом активных процессов на Солнце (например, вспышек).

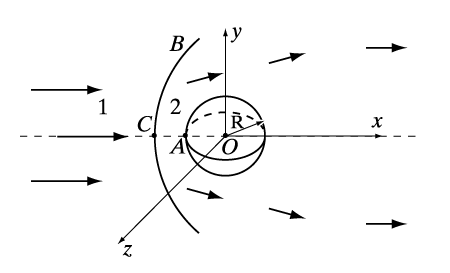
Известно, что около пассажирских самолетов, летающих главным образом с большими дозвуковыми, никакие ударные волны не образуются. Пусть есть сферическое тело радиуса R (рис. 6), которое летит в воздухе со сверхзвуковой скоростью. Тогда впереди такого тела образуется ударная волна В, являющаяся границей между областями 1 и 2, которые отличаются значениями параметров газа. В системе координат, связанной с летящим телом. поток газа набегает на покоящееся тело. Пусть ось Оx направлена вдоль скорости потока, а V₁, p₁, r1 и T₁ – скорость, давление, плотность и температура, соответственно, в невозмущенном телом потоке газа (до ударной волны). В область 1 возмущения от тела не попадают, поскольку тело движется со сверхзвуковой скоростью. Так как скорость газа в лобовой точке тела А обращается в нуль, то от точки А до точки С на ударной волне есть область дозвуковой скорости газа, которой достигают возмущения воздуха от летящего тела. Физический смысл образования ударной волны и заключается в разделении невозмущенного и возмущенного потоков газа. Если через V₂, p₂, r2 и T₂ обозначить скорость, давление, плотность и температуру газа соответственно сразу же после ударной волны В, то справедливы неравенства

Это означает, что скорость за ударной волной уменьшается, а давление, плотность и температура возрастают. Сильным возрастанием температуры за ударной волной и объясняется оплавление возвращающихся на Землю космических аппаратов и метеоритов, вторгающихся в атмосферу с большими сверхзвуковыми скоростями. Такие ударные волны называются ударными волнами сжатия (плотность газа возрастает). Интересно, что в природе никогда не наблюдались ударные волны разрежения, в которых плотность падает. Математически образование ударных волн разрежения запрещается известной в гидроаэромеханике теоремой Цемплена

Соотношения между параметрами с индексами «1» и «2» можно получить из интегральных законов сохранения массы, импульса и энергии, поскольку они справедливы и для разрывных функций. Такие соотношения называются соотношениями Гюгонио и имеют вид (в системе координат, связанной с ударной волной)

Вместе с уравнением состояния эти соотношения позволяют определить значения параметров газа за ударной волной (индекс «2») по значениям параметров невозмущенного ударной волной потока газа (индекс «1»).

Описанный математический аппарат гидроаэромеханики используется во многих областях естественных наук, при этом для корректности использования этого аппарата требуется только выполнение критерия сплошности среды, т.е. для газов, например, длина свободного пробега частиц должна быть много меньше характерных размеров рассматриваемых объектов обтекания. В частности, в условиях космического пространства часто среда очень разрежена. В таких средах, конечно же, длина свободного пробега частиц очень велика, но размеры самих объектов исследования оказываются во многих случаях существенно больше, т.е. методы гидроаэромеханики применимы и к таким объектам.

В биомеханике при помощи методов гидромеханики исследуются интересные особенности течений биологических жидкостей по сосудам, а в гидрогеологии исследуются, например, задачи динамики внутренних слоев Земли. Все это свидетельствует о важности науки, которая называется «гидроаэромеханика».

Ландау Л.Д. и Лифшиц Е.М. Механика сплошных сред. М., ГИТТЛ, 1954
Чепмен С. и Каулинг Т. Математическая теория неоднородных газов. ИИЛ, М., 1960
Кочин Н.Е., Кибель и Розе. Теоретическая гидромеханика, т.1. Физматгиз, 1963
Кочин Н.Е., Кибель и Розе, Теоретическая гидромеханика, т.2, Физматгиз, 1963
Седов Л.И. Механика сплошной среды. М., Наука, т. 1, 1973
Седов Л.И. Механика сплошной среды. М., Наука, т. 2, 1973
Баранов В.Б. и Краснобаев К.В., Гидродинамическая теория космической плазмы, М., Изд. «Наука», 1977
Эйлер Л. Общие законы движения жидкостей. Известия РАН, сер. МЖГ, 1999, № 6

Видео:Горбачев В. И. - Основы механики сплошных сред. Часть 2 - Основные уравнения из законов сохраненияСкачать

Лекция 2

Видео:Основы гидродинамики и аэродинамики | условие неразрывностиСкачать

Автор —

Уравнение движения идеальной жидкости Эйлера

Выделим в движущейся в поле сил тяжести идеальной (невязкой) жидкости произвольный объём V , ограниченный поверхностью S с единичной внешней нормалью n. Найдём сумму внешних сил, действующих на данный объём.

Поскольку в идеальной жидкости действуют только нормальные напряжения, сила давления, действующая на выделенный объём со стороны окружающей жидкости равна интегралу

(в соответствии с уравнением (1))

Преобразуя поверхностный интеграл в объёмный, получим

На данный объём действует также внешняя сила тяжести, равная интегралу

где — сила тяжести единичного объёма.

Таким образом, сумма внешних сил, действующих на объём V, равна интегралу

Из этого выражения видно, что на каждый элемент объёма dV действует сила

Из механики известно, что сумма внешних сил, действующих на тело, равна произведению массы тела на его ускорение, следовательно

Сократив на величину dV, получим уравнение движения идеальной жидкости Эйлера

(28)

Запишем уравнение движения Эйлера в проекциях на оси координат

(29)

Индивидуальные производные проекций скорости находятся по формуле (21).

Например, для проекции скорости на ось x, получим

Для несжимаемых невязких жидкостей решение уравнения (28) совместно с уравнением неразрывности (17) позволяет определить четыре неизвестных , , ,P.

Для изотермических процессов при значительном изменении давления в идеальных сжимаемых жидкостях, при решении аналогичной задачи, кроме уравнений (28) и (15) требуется знание зависимости плотности от давления

(30)

(Жидкости, у которых плотность подчиняется уравнению (32) называются баротронными).

Следует отметить, что случаи, когда необходим учёт сжимаемости при решении таких задач, в химической технологии достаточно редкие.

РАВНОВЕСИЕ ЖИДКОСТИ В ПОЛЕ СИЛЫ ТЯЖЕСТИ.

В покоящейся жидкости (реальной и идеальной) как и в движущейся идеальной жидкости действуют только нормальные напряжения с идентичными свойствами. Поэтому, приравняв скорость нулю в уравнении (28), получим уравнение равновесия Эйлера жидкости в поле сил тяжести

(31)

В проекциях на оси координат уравнение (31) превращается в систему уравнений

(32)

Так как производные давления по x и y равны нулю, для несжимаемой жидкости получим

Отсюда получим основное уравнение гидростатики

(33)

Запишем уравнение (33) для ряда сечений покоящейся жидкости

(34)

Основное уравнение гидростатики (33) можно также записать в следующей форме

(35)

или (36)

Все составляющие этого уравнения имеют размерность длины и называются напорами или высотами, кроме того, их можно рассматривать как величины удельной (отнесённой к единице веса) потенциальной энергии

– пьезометрический напор (пьезометрическая высота), м.

z – геометрический напор (нивелирная высота), м.

Из уравнения (36) следует, что сумма пьезометрического и геометрического напора для любой точки покоящейся жидкости есть величина постоянная.

Основное уравнение гидростатики служит для определения величин давления, положений раздела фаз в покоящихся жидкостях, а также для определения сил, действующих на дно и стенки аппаратов.

Рассмотрим применение основного уравнения гидростатики на примере простейшего U-образного манометра ( Рис.4), который представляет собой прибор (1) в виде прозрачной трубки, заполненной манометрической жидкостью.

Манометр присоединён к аппарату, содержащему газ, плотность которого пренебрежительно мала по сравнению с плотностью манометрической жидкости.

Уровни жидкости в U-образной трубке z1 и z2, причём давление на уровне z2 атмосферное Р2 = Ратм.

Уравнения движения и равновесия идеальной несжимаемой жидкости в однородном поле силы тяготения

Рис.4. Измерение давления U — образным манометром

Запишем уравнение (34) для двух уровней жидкости

Если давление в аппарате выше атмосферного z2 > z1, найдём избыточное давление в аппарате по сравнению с атмосферным

Избыточное давление (Ризб) равно разнице между абсолютным давлением в аппарате (Р абс = Р1) и атмосферным.

(37)

Если давление в аппарате ниже атмосферного, уровень z1 будет выше уровня z2, тогда можно записать

Эта величина (Рвак), называемая разряжением или вакуумом, равна разнице между атмосферным давлением и абсолютным давлением в аппарате.

(38)

Для сжимаемых жидкостей уравнение интегрируют совместно с уравнением состояния.

В случае баротронных жидкостей получим

(40)

При использовании уравнения (40) следует иметь в виду, что оно даёт существенные расхождения с уравнением (34) только для больших масс (высоких слоёв) сжимаемых жидкостей.

Энергетический баланс потока идеальной жидкости

Рассмотрим стационарное движение физически бесконечно малого объёма идеальной жидкости по линии тока, как известно, совпадающей с траекторией движения этой жидкой частицы. В проекциях на оси координат это движение описывается системой уравнений Эйлера(29).

Умножим правые и левые части системы уравнений (29) на соответствующие проекции элементарного пути пройденного частицей: dx, dy, dz

(40)

Просуммировав левые и правые части этих уравнений с учетом того, что

, , получим

(41)

В случае несжимаемой жидкости уравнение (41) упрощается

, следовательно

(42)

Чаще это уравнение записывают в таком виде

(43)

Величина константы с меняется для различных линий тока.

Таким образом, получено уравнение энергетического баланса движения элементарного объёма несжимаемой идеальной жидкости по линии тока, называемое уравнением Бернулли. Согласно этому уравнению сумма удельной (отнесённой к единице веса) кинетической энергии () и потенциальной энергии давления и положения () есть величина постоянная для любой точки на линии тока.

Величины удельных энергий также называют напорами, как и в уравнении гидростатики (36) с добавлением скоростного напора.

— скоростной или динамический напор, м.

Для конечных сечений потока параметры уравнения (43) осредняют по всем линиям тока, т. е. по всему сечению, при этом вместо скорости в точке используют среднюю скорость по поперечному сечению (wср), поэтому удельная кинетическая энергия, рассчитанная по средней скорости, умножается на поправочный коэффициент a, зависящий от распределения скорости по сечению потока

(44)

В технических расчётах обычно принимают a =1 по следующим причинам. Величина a при больших скоростях турбулентного течения незначительно превышает 1; при малых скоростях, соответствующих ламинарному движению a = 2. Но поскольку сама величина кинетической энергии в этом случае очень мала по сравнению с величинами потенциальной энергии, приравнивание a единице не вносит существенных погрешностей в расчёты.

При средних скоростях турбулентной области из-за сравнительно малой величины кинетической энергии погрешности также незначительны.

Таким образом, получим уравнение Бернулли для конечных сечений потока несжимаемой идеальной жидкости.

В технических расчётах обычно используют средние по сечению величины скоростей, поэтому принимаем обозначения wср= w, тогда уравнение Бернулли принимает вид

(45)

Следовательно, для любых сечений, получим

(46)

В случае сжимаемой жидкости уравнение (41) записывается в виде:

(47)

Чтобы решение этого уравнения имело вид аналогичный уравнению Бернулли для идеальной несжимаемой жидкости используют следующую функцию

где Ро – значение давления в начальной точке линии тока, или, для конечных сечений, в начальном сечении.

Величину этой функции определяют по известной зависимости

Проинтегрировав уравнение (47), получим уравнение Бернулли для сжимаемой идеальной жидкости

(48)

где С – константа.

В технических расчётах уравнение (48) используется очень редко, в случаях очень больших скоростей, сравнимых со скоростью звука, так как при обычных скоростях газа, расчёты проведенные по уравнениям (43) и (48) для сжимаемых и несжимаемых жидкостей не дают существенных расхождений.

Видео:Лекция 12. Элементы гидродинамикиСкачать

ЛЕКЦИЯ №2. Однородная несжимаемая жидкость

Это равновесие описывается уравнением, которое называется основным уравнением гидростатики. Наша цель — получить это уравнение.

Если рассмотреть сосуд с покоящейся жидкостью, то на нее действует сила атмосферного давления р и ? = g М (сила ее массы). Что касается плотности этой силы Q, то это F = g.

Выразим в декартовой системе координат:

Учтя (40), в (34) получим:

Поскольку, р = const, и изменением g от высоты в данном случае пренебрегаем, то есть g = const, то проинтегрировав (41), получим:

где с — постоянная интегрирования.

Следим, как поведет себя уравнение (42) в случае, если мы его применим к единице веса.

Для этого разделим его на pg’:

Если относить уравнение (42) к единице массы, то придется разделить ее на р

Если рассмотрим полученные уравнения для любых двух точек одного и того же объема, то

Полученные уравнения описывают распределение давления в жидкости, которая находится в равновесном состоянии. Из них уравнение (45) является основным уравнением гидростатики.

Для водоемов больших объемов или поверхности требуется уточнения: сонаправлен ли g радиусу Земли в данной точке; насколько горизонтальна рассматриваемая поверхность.

Возьмем любую точку А, высота которой z, со значением давления р в этой точке, которое и нужно определить.

Для этого возьмем точку В на свободной поверхности с высотой г₀ и сдавлением p_Q. Используя эту точку, определим р, причем по сравнению с атмосферным р₀ р_атм, р₀ = р_атц.

Согласно уравнению (45)

Очевидно, что Zq — Z = h — высота, которая характеризует глубину погружения точки А под свободную поверхность. Следовательно,

где pgh — весовое давление, которое соответствует единичной высоте и единичной площади.

Другими словами, давление в точке А является суммой внешнего давления (в данном случае р₀) и веса столба pgh.

Нередко давление р называют абсолютным давлением р_абс.

Если р > р_а6с, то р — р_атм = р₀ + pg/i — р_атм — его называют из-быточным давлением:

называют вакуумметрическим давлением.

На свободной поверхности и р₀ = р_атм, поэтому

Что произойдет в других точках жидкости, если приложим некоторое усилие Др ? Если выбрать две точки, и приложить к одной из них усилие Др,, то согласно формуле (45), то есть по основному уравнению гидростатики, во второй точке давление изменится на Др₂.

откуда легко заключить, что при равности прочих слагаемых должно быть

Мы получили выражение закона Паскаля, который гласит: изменение давления в любой точке жидкости в равновесном состоянии передается во все остальные точки без изменений.

До сих пор мы исходили из предположения, что р = const. Если иметь сообщающийся сосуд, который заполнен двумя жидкостями с Р] # р₂, причем внешнее давление p_Q = р, = р_атч, то со-

гдс Л], Л₂ — высота от раздела поверхности до соответствующих свободных поверхностей.

Единицы измерения давления

Мы до сих пор не дали определения давлению: давление — физическая величина, которая характеризует силы, направленные по нормали к поверхности одного предмета со стороны другого.

Если силы распределены нормально и равномерно, то давление

где F — суммарная приложенная сила;

S — поверхность, к которой приложена сила.

Если силы распределены неравномерно, то говорят о среднем значении давления или считают его в отдельно взятой точке: например, в вязкой жидкости.

Для того, чтобы определить среднее значение давления нужно суммировать его проекции по осям.

Давление измеряется с помощью пьезометров, манометров и вакуумметров, о которых расскажем чуть позже.

Единицы измерения давления следующие:

I Паскаль — 1 Н/м 2

1 Бар — 1О 5 дин/см 2

кг х с/см 2 — 1 атмосфера

1 Атм. — 760 мм рт.ст.

Мм рт. ст. — высота столбца с ртутью

Мм вод. ст. — высота столбца с водой.

Если говорить о физическом смысле единицы Паскаль, то это сила в 1 Ньютон, приложенная к площади 1 кв. м.

Преобразовав 1 паскаль = 1 II м/м 3 , получим I Дж/м 3 .

При измерении больших давлений используют единицу мега паскаль (МПа).

Приборы для измерения давления

Одним из приборов, которым измеряют давление, и о котором сказано выше, является манометр. Это U-образная стеклянная труба диаметром 10— 15 мм. Один конец трубы свободный, другой конец присоединяется к точке, в которой необходимо измерять давление. Разность давлений в концах трубки р-> — р_х может быть уравновешена противодавлением pgh (или весовым давлением), то есть:

Как видно из (59), достаточно знать высоту А, поскольку р_х задано, чтобы вычислить р₂.

Для определения на трубы прикрепляется специальная шкала.

Недостатком манометров является то, что у них небольшой диапазон измерений: 1 — 10 кПа.

По этой причине в трубах используют жидкости, которые «уменьшают» высоту, например, ртуть.

Например, если требуется измерять давление 1,5 атм (0,15 МПа), то требуется манометр, трубы у которого имеют высоту 15 мм.

Ртуть же уменьшает эту высоту в 13,6 раз.

Для измерения еще больших давлений пользуются пружинными манометрами.

Следующим прибором для измерения давления является пьезометр. Возможно, кому-то из вас пришлось проделать следующий опыт: если возьмем резиновую или хлорвиниловую трубку произвольной длины, заполним водой, затем, закрыв один конец пальцем, оставим другой конец свободным и поднимем трубку, вода не выльется.

Вода не будет выливаться, даже если между жидкостью и другим закрытым концом будет воздушный зазор; может даже подниматься к закрытому концу трубы. Вот это последнее зависит от атмосферного или другого, если проводится специальный эксперимент, давления. Именно по этому принципу работают пьезометры: на свободный конец трубы действует измеряемое давление.

Это же является причиной того, почему в узкой трубе уровень жидкости выше, чем в самом сосуде.

Сосуд и ответвление от него на глубине h_A со свободной поверхностью, образуют систему сообщающихся сосудов.

Высота свободной поверхности в узкой трубке поднимается на It_н > h_A потому, что атмосферное давление р_> > р₂, где р₂ — соответствующие давления, действующие на свободные поверхности сосуда и трубы. р_<> р₂ потому, что площадь свободной поверхности у сосуда больше, чем у трубы, причем разность давлений Р— р->

h_H. Высоту напора принято называть пьезометрической высотой, или напором.

Рассмотрим следующие случаи.

1. Мы уже видели, что происходит при р, > h_H > h_A, h_A — потому что трубка соединена с сосудом на уровне точки А.

Для нахождения h_H воспользуемся условием равновесной жидкости. В данном случае система представляет собой равновесную систему.

Согласно основному уравнению гидростатики,

где р — плотность жидкости;

g — ускорение свободного падения.

р₂, как правило, задается р₂ = р_атм, поэтому, зная h_A и h_H, нетрудно определить искомую величину.

2. Р = Р1 = Ратм’ Совершенно ОЧЄВИДНО, ЧТО ИЗр= COnSt, g = const следует, что h_A = h_H. Этот факт называют также законом сообщающихся сосудов.
3. /’, = Pe + Pg h — 60 >

Теперь несложно определить высоту, которая и является характеристикой изменения вакуума:

Как следует из этой же формулы, png постоянные, h — характеристика степени разреженности в приборе. р_вак = р_а + р_в — такова разность между атмосферным давлением и давлением в трубке.

Вакуум измеряется в тех же единицах, что и давление.

Вернемся к основному гидростатическому уравнению. Здесь z — координата рассматриваемой точки, которая отсчитывается от плоскости XOY. В гидравлике плоскость XOY называется плоскостью сравнения.

Отсчитанную от этой плоскости координату z называют по-разному: геометрической высотой; высотой положения; геометрическим напором точки z-

В том же основном уравнении гидростатики величина p/pgh — также геометрическая высота, на которую поднимается жидкость в результате воздействия давления р.

p/pgh так же, как и геометрическая высота, измеряется в метрах. В случае, если через другой конец трубы на жидкость действует атмосферное давление, то жидкость в трубе поднимается на высоту p_U36/pgh. которую называют вакуумметрической высотой.

Высоту, соответствующую давлению р_вак, называют вакуумметрической.

В основном уравнении гидростатики сумма z + p/pgh — гидростатический напор Я, различают также пьезометрический напор Н_п, который соответствует атмосферному давлению P_amJpgh’.