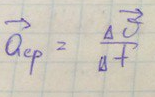Уравнения движения и графики x t vx t s t для равномерного прямолинейного (7 видео)

Содержание

Уравнение движения, графики равномерного прямолинейного движения
п.1. Прямолинейное равномерное движение на координатной прямой
п.2. Уравнение прямолинейного равномерного движения
п.3. Удобная система отсчета для решения задачи о прямолинейном движении
п.4. График движения x=x(t)
п.5. Как найти уравнение движения по графику движения?
п.6. График скорости vx=vx(t)
п.7. Как найти путь и перемещение по графику скорости?
п.8. Задачи
Абсолютно упругий удар – соударение, при котором сохраняется полная кинетическая энергия системы.
Уравнения движения и графики x t vx t s t для равномерного прямолинейного
А теперь к задачам!
Графики равномерного прямолинейного движения (Ерюткин Е.С.)
📽️ Видео

Видео:Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Уравнение движения, графики равномерного прямолинейного движения

п.1. Прямолинейное равномерное движение на координатной прямой

Система отсчета, с помощью которой можно описать прямолинейное движение состоит из:
1) тела отсчета; 2) координатной прямой; 3) часов для отсчета времени.
Пусть телом отсчета будет дом.
В начальный момент времени машина стоит в 20 м справа от дома.

Рассмотрим движение машины со скоростью 10 м/с вправо.
Направим координатную прямую параллельно вектору скорости, вправо.

Составим таблицу перемещений за первые 4 секунды:

t, c	0	1	2	3	4
x, м	20	30	40	50	60

Стартуя с точки x₀=20, машина каждую секунду удаляется от дома еще на 10 м.
Пройденный путь за 2 секунды – 10·2=20 м, за 3 секунды – 10·3=30 м, за t секунд s=vt метров. Значит, для произвольного времени t можем записать координату x в виде: begin x=x_0+s=x_0+vt\ x=20+10t end

Если при тех же начальных условиях и направлении координатной прямой машина будет двигаться влево, получим таблицу:

t, c	0	1	2	3	4
x, м	20	10	0	-10	-20

В этом случае координата x в любой момент времени t имеет вид: begin x=x_0-st=x_0-vt\ x=20-10t end Если же машина никуда не едет, её скорость v=0, и координата x=x₀ в любой момент времени t.

п.2. Уравнение прямолинейного равномерного движения

Зависимость координаты тела от времени в механике называют уравнением движения.
Если уравнение движения известно, то мы можем решить основную задачу механики.

п.3. Удобная система отсчета для решения задачи о прямолинейном движении

При решении задачи можно выбрать различные тела отсчета и связать с ними различные системы координат. Как правило, некоторая система отсчета является наиболее удобной для решения данной задачи в том смысле, что в ней уравнение движения выглядит и решается проще, чем в других системах.

При решении задач на прямолинейное движение телом отсчета может быть неподвижная поверхность (земля, пол, стол и т.п.), само движущееся тело или другое тело.
При этом системой координат является координатная прямая, параллельная направлению движения (вектору перемещения) тела, уравнение движения которого мы хотим получить.

Проекции скорости и перемещения на координатную прямую могут быть положительными, равными нулю или отрицательными. Величины скорости и перемещения будут равны длинам соответствующих проекций.

п.4. График движения x=x(t)

Сравним полученное уравнение движения (x(t)=x_0+v_x t) с уравнением прямой (y(x)=kx+b) (см. §38 справочника по алгебре для 7 класса).

В уравнении движения роль углового коэффициента (k) играет проекция скорости (v_x), а роль свободного члена (b) – начальная координата (x_0).

Уравнения движения и графики x t vx t s t для равномерного прямолинейного

Построим графики зависимости координаты от времени для нашего примера:

x=20+10t — машина движется вправо (в направлении оси OX)
x=20-10t — машина движется влево (в направлении, противоположном оси OX)
x=20 — машина стоит

п.5. Как найти уравнение движения по графику движения?

п.6. График скорости v_x=v_x(t)

Для рассмотренного примера:

п.7. Как найти путь и перемещение по графику скорости?

Пусть тело движется прямолинейно равномерно, зависимость его координаты от времени описывается уравнением: $$ x(t)=x_0+v_x t $$ Тогда в некоторый момент времени (t_1) координата равна (x_1=x_0+v_x t_1).
Несколько позже, в момент времени (t_2gt t_1) координата равна (x_2=x_0+v_x t_2).
Если (v_xgt 0), то пройденный за промежуток времени (triangle t=t_2-t_1) путь равен разности координат: $$ s=x_2-x_1=(x_0+v_x t_2)-(x_0+v_x t_1)=x_0-x_0+v_x (t_2-t_1)=v_x triangle t $$ В общем случае, т.к. (v_x) может быть и отрицательным, а путь всегда положительный, в формуле нужно поставить модуль: $$ s=|v_x|triangle t $$
Изобразим полученное соотношение на графике скорости:

Проекция скорости (v_x) может быть не только положительной, но и отрицательной.
Если учитывать знак, то произведение: $$ triangle x=v_x triangle t $$ дает проекцию перемещения на ось OX. Знак этого произведения указывает на направление перемещения.

Проекция перемещения может быть как положительной, так и отрицательной или равной 0.

п.8. Задачи

Задача 1. Спортсмен бежит по прямолинейному участку дистанции с постоянной скоростью 8 м/с. Примите (x_0=0) и запишите уравнение движения.
а) Постройте график движения (x=x(t)) и найдите с его помощью, сколько пробежит спортсмен за (t_1=5 с), за (t_2=10 с);
б) постройте график скорости (v=v(t)) и найдите с его помощью, какой путь преодолеет спортсмен за промежуток времени (triangle t=t_2-t_1)?

По условию (x_0=0, v_x=8).
Уравнение движения: (x=x_0+v_x t=0+8t=8t)
а) Строим график прямой (x=8t) по двум точкам:

t	0	5
x	0	40

По графику находим: begin x_1=x(5)=8cdot 5=40 text\ x_2=x(10)=8cdot 10=80 text end
б) Скорость (v_x=8) м/с — постоянная величина, её график:

$$ t_1=5 с, t_2=10 с $$ Пройденный путь за промежуток времени (triangle t=t_2-t_1) равен площади заштрихованного прямоугольника: $$ s=v_x triangle t=8cdot (10-5)=40 text $$ Ответ: а) 40 м и 80 м; б) 40 м

Задача 2. Космический корабль движется прямолинейно с постоянной скоростью.
Известно, что через 1 час после старта корабль находился на расстоянии 38 тыс.км от астероида Веста, а через 2 часа после старта – на расстоянии 56 тыс.км.
а) постройте график движения корабля, найдите по графику уравнение движения.
б) на каком расстоянии от астероида находился корабль в начальный момент времени?
в) на каком расстоянии от астероида будет находиться корабль через 4 часа после старта?
г) чему равна скорость корабля в километрах в секунду?

а) Будем откладывать время в часах, а расстояние в тыс.км
Отмечаем точки A(1;38) и B(2;56), проводим через них прямую.
Полученная прямая и есть график движения (x=x(t)).

Найдем скорость корабля (v_x): $$ v_x=frac=frac=18 (text) $$ Найдем начальную координату (x_0): $$ x_0=x_1-v_x t_1=38-18cdot v_1=20 (text) $$ Получаем уравнение движения: $$ x(t)=x_0+v_x t, x(t)=20+18t $$ где (x) – в тыс.км, а (t) – в часах.

б) В начальный момент времени корабль находился на расстоянии (x_0=20) тыс.км от астероида.

в) Через 4 часа после старта корабль будет находиться на расстоянии $$ x(4)=20+18cdot 4=92 (text) $$
г) Переведем скорость в км/с: $$ 18000frac<text><text>=frac<18000 text><1 text>=frac<18000 text><3600 text>=5 text $$ Ответ:
а) (x(t)=20+18t) ((x) в тыс.км, (t) в часах); б) 20 тыс.км; в) 92 тыс.км; г) 5 км/с

Видео:9 класс, 3 урок, Графики прямолинейного равномерного движенияСкачать

Абсолютно упругий удар – соударение, при котором сохраняется полная кинетическая энергия системы.

Зачет по физике 1 полугодие 2015-2016 10 класс.

Билет 1.

1. Система отсчета, материальная точка. Траектория, путь, перемещение. Средняя скорость, среднепутевая скорость, мгновенная скорость. Прямолинейное равномерное движение. Уравнения движения и графики x(t), v_x(t), s(t) для равномерного прямолинейного движения.

Система отсчета – совокупность тела отсчета, связанной с ним системы координат и часов.

Материальная точка – тело размерами и формой которого можно пренебречь в условиях данной задачи.

Траектория – линия по которой точка движется в пространстве.

Путь — длина участка траектории материальной точки, пройденного ею за определенное время.

Перемещение тела – направленный отрезок, проведенный из начального положения тела в его конечное положение.

Средней скоростью перемещения называется векторная величина равная отношению перемещения к промежутку времени, за который это перемещение произошло.

Средней путевой скоростью называется скалярная величина равная отношению пути пройденного материальной точкой к промежутку времени.

Мгновенная скорость— векторная физическая величина, равная пределу отношения вектора перемещения к промежутку времени за которое это перемещение произошло, при -> к нулю.

Равномерное прямолинейное движение – движение при котором тело за любые равные промежутки времени совершает одинаковое перемещение.

— уравнение равномерного прямолинейного движения точки.

— уравнение прямолинейного равномерного движения.

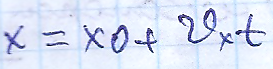
Сформулируйте условия равновесия твердого тела. Запишите соответствующие им аналитические выражения и укажите единицы входящих в них величин.

Условия равновесия твердого тела:необходимым и достаточными условиями равновесия свободного твердого тела является равенство нулю векторной суммы всех внешних сил, действующих на тело, равенство нулю суммы всех моментов внешних сил относительно произвольной оси, равенство нулю начальной скорости поступательного движения тела и условие равенства нулю начальной угловой скорости вращения.

Почему нагруженный автомобиль на булыжной мостовой движется более плавно, чем такой же автомобиль без груза?

1.Увеличение массы автомобиля уменьшает ускорения, сообщаемые ему толчками камней булыжной мостовой.
2.У нагруженного инертность больше

Когда расходуется больше энергии – при запуске спутника вдоль меридиана или вдоль экватора?

При запуске спутника вдоль экватора в сторону вращения Земли линейная скорость суточного вращения складывается со скоростью, сообщенной спутнику двигателем ракеты. Естественно, при запуске вдоль меридиана (а тем более вдоль экватора в сторону, обратную вращению Земли) потребуется больше энергии для сообщения спутнику первой космической скорости.

Билет 2.

1. Ускорение, единицы ускорения. Среднее и мгновенное ускорение. Прямолинейное равнопеременное движение. Уравнения движения и графики x(t), v_x(t), a_x(t), s(t) для прямолинейного равнопеременного движения. Свободное падение.

Ускорение тела – предел отношения изменения скорости к промежутку времени, в течение которого это изменение произошло.

Модуль ускорения численно равен единице, если за единицу времени модуль вектора изменения скорости изменяется на единицу.

Среднее ускорение – это векторная физическая величина равная отношению вектора к промежутку времени за которое это изменение произошло.

Мгновенное ускорение(ускорение) в данной точке траектории это векторная величина, равная пределу отношения скорости материальной точки к промежутку времени , в течении которого это изменение произошло, при -> к нулю.

Ускорение может быть направленно под любым углом к касательной траектории движения.

Равнопеременное прямолинейное движение – движение с постоянным по модулю и направлению ускорением.

– кинематическое уравнение движение

– уравнение равнопеременного (равноускоренного) движения

Какие столкновения называются упругими? Что такое центральные и нецентральные столкновения? Получите формулы скоростей движения шаров после упругого центрального столкновения.

Абсолютно упругий удар – соударение, при котором сохраняется полная кинетическая энергия системы.

Центральным ударом называется удар, если в момент столкновения тел их скорости направлены вдоль линии, соединяющей их центры масс.

Нецентральным ударом называется удар, если в момент столкновения тел их скорости не направлены вдоль линии, соединяющей их центры масс.

Видео:Решение графических задач на равномерное движениеСкачать

Уравнения движения и графики x t vx t s t для равномерного прямолинейного

Задачи по физике — это просто!

Не забываем, что решать задачи надо всегда в системе СИ!

А теперь к задачам!

Элементарные задачи из курса школьной физики по кинематике.

Задача на составление описания движения и составление уравнения движения по заданному графику движения

Дано: график движения тела

Найти:
1. составить описание движения
2. составить уравнение движения тела.

Проекцию вектора скорости определяем по графику, выбрав любой удобный для рассмотрения отрезок времени.
Здесь удобно взять t=4c

Составляем уравнение движения тела:

Записываем формулу уравнения прямолинейного равномерного движения.

Подставляем в нее найденный коэффициент V_x (не забываем о минусе!).
Начальная координата тела (X_о) соответствует началу графика, тогда X_о=3

Составляем описание движения тела:

Желательно сделать чертеж, это поможет не ошибиться!
Не забываем, что все физические величины имеют единицы измерения, их необходимо указывать!

Тело движется прямолинейно и равномерно из начальной точки X_о=3м со скоростью 0,75 м/с противоположно направлению оси X.

Задача на определение места и времени встречи двух движущихся тел (при прямолинейном равномерном движении)

Движение тел задано уравнениями движения для каждого тела.

Дано:
1. уравнение движения первого тела
2. уравнение движения второго тела

Найти:
1. координату места встречи
2. момент время (после начала движения), когда произойдет встреча тел

По заданным уравнениям движения строим графики движения для каждого тела в одной системе координат.

Точка пересечения двух графиков движения определяет:

1. на оси t — время встречи ( через сколько времени после начала движения произойдет встреча)
2. на оси X — координату места встречи (относительно начала координат)

В результате:

Два тела встретятся в точке с координатой -1,75 м через 1,25 секунд после начала движения.

Для проверки полученных графическим способом ответов можно решить систему уравнений из двух заданных
уравнений движения:

Для тех, кто почему-то забыл, как построить график прямолинейного равномерного движения:

График движения — это линейная зависимость ( прямая), строится по двум точкам.
Выбираем два любых удобных для простоты расчета значения t₁ и t₂.
Для этих значений t подсчитываем соответствующие значения координат X₁ и X₂.
Откладываем 2 точки с координатами (t₁, X₁) и (t₂, X₂) и соединяем их прямой — график готов!

Задачи на составление описания движения тела и построение графиков движения по заданному уравнению прямолинейного равномерного движения

Задача 1

Дано: уравнение движения тела

Найти:
1. составить описание движения
2. построить график движения

Заданное уравнение сравниваем с формулой и определяем коэффициенты.
Не забываем делать чертеж, чтобы еще раз обратить внимание на направление вектора скорости.

Задача 2

Дано: уравнение движения тела

Найти:
1. составить описание движения
2. построить график движения

Задача 3

Дано: уравнение движения тела

Найти:
1. составить описание движения
2. построить график движения

Задача 4

Дано: уравнение движения тела

Найти:
1. составить описание движения
2. построить график движения

Тело находится в состоянии покоя в точке с координатой X=4м (состояние покоя — это частный случай движения, когда скорость тела равна нулю).

Задача 5

Дано:
начальная координата движущейся точки xo=-3 м
проекция вектора скорости Vx=-2 м/с

Найти:
1. записать уравнение движения
2. построить график движения
3. показать на чертеже векторы скорости и перемещения
4. найти координату точки через 10 секунд после начала движения

Видео:Урок 12. Равномерное прямолинейное движениеСкачать

Графики равномерного прямолинейного движения (Ерюткин Е.С.)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы изучим графики равномерного прямолинейного движения. С помощью графиков движения вы сможете более ясно представить себе картину происходящего с телом. Мы научимся строить графики, используя законы движения, и, наоборот, имея графики, определять по ним параметры движения. Кроме того, мы научимся определять путь, пройденный телом, используя график зависимости скорости тела от времени.