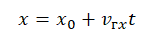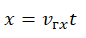Уравнения движения двух автомобилей x1 30t 10 и x2 50 10t

Угловое ускорение
ω = φ’ = A + 3Bt²
ω = 2+3*0,2*3² = 7,4 рад/с
Нормальное ускорение
an = ω²R
an = 7,4²*0,5 = 27,38 м/с²
Линейная скорость
v = ωR
Тангенциальное ускорение
aτ = v’=ω’R = 6Bt*R
aτ = 6*0,2*3*0,5 = 1,8 м/с²
Полное ускорение
a = √ (an² + aτ²)
a = √ (27,38² + 1,8²) ≈ 27,44 м/с²

Угловое ускорение
ω = φ’ = 2Bt + 3Ct²
ω = 2*(-1)*10 + 3*0,1*10² = -20+30 = 10 рад/с
Нормальное ускорение
an = ω²R
an = 10²*0,2 = 20 м/с²
Линейная скорость
v = ωR
Тангенциальное ускорение
aτ = v’=ω’R = (2B + 6Ct)R
aτ = (2*(-1)+6*0,1*10)*0,2 = (-2+6)*0,2=0,8 м/с²
Полное ускорение
a = √ (an² + aτ²)
a = √ (20² + 0,8²) ≈ 20,02 м/с²

Видео:Движение двух велосипедистов задано уравнениями x1=2t (м) и x2=100-8t (м) - №22625Скачать

Контрольная работа№2: «Прямолинейное равноускоренное движение»

Контрольная работа№2: «Прямолинейное равноускоренное

Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Вариант №1 К-Мех.2

1. Автомобиль, скорость которого 10 м/с, начал двигаться с постоянны по модулю ускорением 0,5 м/с2 направленным в сторону движения. Определите скорость автомобиля через 20 с.

2. Скорость задана уравнением vx = 8 + 2t, построить графики зависимости аx(t) и vx(t).

3. На рисунке показан вектор ускорения. Каков характер движения, если тело движется влево? вправо?

4. Пуля, летящая со скоростью 600 м/с, застревает в бетонной стене. Найдите глубину проникновения пули, если она двигалась в бетоне 0,001 с. Движение в бетоне считать равноускоренным. Какова средняя скорость пули в бетоне?

Видео:Решение графических задач на равномерное движениеСкачать

Вариант №2 К-Мех.2

1. Автомобиль двигался равноускоренно, и в течение 10 с его скорость увеличилась с 18 до 54 км/ч. Найти ускорение автомобиля.

2. Уравнение движения тела имеет вид x = 20 + 5t – 0,5t2. Постройте графики зависимости ax(t) и vx(t). Чему равна скорость тела через 10 с после начала отсчета времени?

3. Какую скорость переменного движения показывает спидометр автомобиля?

4. Первый вагон трогающегося от остановки поезда проходит за 3 с мимо наблюдателя, находившегося до отправления поезда у начала этого вагона. За сколько времени пройдёт мимо наблюдателя весь поезд, состоящий из 9 вагонов? Промежутками между вагонами пренебречь.

Видео:Урок 15. Решение задач на графики движенияСкачать

Вариант №3 К-Мех.2

1. Байдарка прошла расстояние 1000 м от старта до финиша со скоростью 5 м/с и после прохождения линии финиша начала тормозить с постоянным ускорением 0,5 м/с2. На каком расстоянии от линии старта окажется байдарка через 10 с после прохождения финишной черты?

2. По графику ускорения изображенному на рисунке дайте характеристику движения тела в течение 9 с, если v0 = 0.

3. О какой скорости идёт речь в следующем примере: скорость движения молотка при ударе о гвоздь равна 8 м/с.

4. Лыжник спускается с горы длина которой 100 м. Сколько времени займёт спуск, если ускорение движения 0,5 м/с2?

Видео:Физика - уравнения равноускоренного движенияСкачать

Вариант №4 К-Мех.2

1. По графику определить ускорение тела, напишите уравнения для скорости и перемещения этого тела. Построй график ускорения.

2. Пуля, при вылете из ствола автомата, имеет скорость 715 м/с. С каким ускорением движется пуля в стволе? Длина ствола 41,5 см.

3. Два поезда идут навстречу друг другу: один – ускоренно на север, другой – замедленно на юг. Как направлены ускорения поездов?

4. Тело падает без начальной скорости с высоты h = 45 м. Какова скорость тела в момент падения на землю? Какова средняя скорость vcp падения на всем пути.

Видео:Задачи на движение двух объектовСкачать

Вариант №5 К-Мех.2

1. При ударе кузнечного молота по заготовке ускорение по модулю равно 200 м/с2. Сколько времени длился удар, если начальная скорость молота была 10 м/с?

2. Построить график скорости для движения двух тел, у которых: а) v0x = 10 м/с; аx = 0; б) v0x = 5 м/с; аx = 2 м/с2. Как зависит скорость от времени в каждом случае? За какое время оба тела совершат одинаковые перемещения?

3. В равноускоренном движении скорость за любые равные промежутки времени изменяется одинаково. Можно ли утверждать, что и путь в этом движении за любые равные промежутки времени изменяется на одно и то же число единиц пути? Ответ обоснуйте.

4. Автомобиль двигался по прямолинейному участку дороги с постоянной скоростью 10 м/с. На расстоянии 100 м от светофора, водитель нажал на тормоз. Найдите положение автомобиля относительно светофора через 2 с после начала торможения, если скорость уменьшилась до 4 м/с.

Видео:Равномерное прямолинейное движение - физика 9Скачать

Вариант №6 К-Мех.2

1. С высоты 5 м, из состояния покоя, упал предмет. Найти его скорость в момент падения на землю.

2. Уравнение движения тела имеет вид x = 128 + 12t – 4t2. Построить графики скорости и ускорения тела. Определить через какой промежуток времени тело остановится.

3. На рисунке показан вектор ускорения. Каков характер движения, если тело движется влево? вправо?

4. Автомобиль после равномерного движения перешел к ускоренному. И двигаясь с ускорением 1,5 м/с2 и за 10 с прошел 195 м. Какова скорость равномерного движения автомобиля и скорость в конце десятой секунды?

Видео:Уравнение движения. Как найти время и место встречи двух тел ???Скачать

Вариант №7 К-Мех.2

1. По уравнению скорости движения v = 5 + 2t, найти перемещение тела за время равное 5 с.

3. О какой скорости (средней или мгновенной) идёт речь в следующих случаях: а) cкоростемер на тепловозе показывает 75 км/ч; б) лесной пожар распространяется со скоростью 25 км/ч; в) ракета достигла скорости 7 км/с.

4. Автомобиль, трогаясь с места, едет с ускорением а1x = 3 м/с2. Достигнув скорости 54 км/ч, он некоторое время едет равномерно, а затем тормозит с ускорением а2x = -5 м/с2 до остановки. Найти время равномерного движения автомобиля, если он прошёл до остановки путь 500 м.

Видео:Задача на среднюю скоростьСкачать

Вариант №8 К-Мех.2

1. Автобус движется со скоростью 54 км/ч. На каком расстоянии от остановки водитель должен начать тормозить, если для удобства пассажиров ускорение не должно превышать 1,2 м/с2.

2. Построить графики скоростей тел уравнения движения, которых имеют вид: v1 = 12 — 3t и v2 = 2t. Через какое время скорости тел станут одинаковыми?

3. Может ли равнозамедленно движущееся тело, иметь положительную проекцию вектора ускорения?

4. Космическая ракета разгоняется из состояния покоя и, пройдя расстояние 200 км, достигает скорости 11 км/с. Каково время разгона ракеты? Движение ракеты считать равноускоренным. Определите среднюю скорость ракеты на всем пути.

Видео:Задачи на движение | Математика TutorOnlineСкачать

Вариант №9 К-Мех.2

1. За 0,1 с скорость космической ракеты увеличилась от 5 до 10 м/с. С каким ускорением она двигалась?

2. Пуля, летящая со скоростью 400 м/с, ударилась о деревянный брус и углубилась в него на 20 см. Сколько времени двигалась пуля внутри бруса?

3. Как движутся поезда 1, 2 и 3 графики которых изображены на рисунке?

4. Поезд отъезжая от станции движется равноускоренно и за 5 мин разгоняется до скорости 54 км/ч. Какое расстояние проходит поезд при разгоне? Определите среднюю скорость движения поезда на пути в 3,24 км от начала движения.

Вариант №10 К-Мех.2

1. Танк, движущийся со скоростью 36 км/ч, натыкается на противотанковый ёж, который заставляет его двигаться с постоянным ускорением аx = -50 м/с2. На каком расстоянии от места столкновения танк остановится.

2. Скорость движения тела задана уравнением vx = 30 -5t, построить график vx(t), найти модуль вектора скорости через 7 с, после начала движения.

3. Какие из приведённых зависимостей описывают равноускоренное движение? 1) vx = 3 + 2t; 2) Sx = 3 + 2t; 3) Sx = 3t2; 4) Sx = 3t — t2; 5) Sx = 2 — 3t + 4t2; 6) vx = 4

4. Парашютист спускается с постоянной скоростью vx = 5 м/с. На расстоянии 10 м от земли у него выпал маленький, но тяжелый предмет. На сколько времени предмет приземлится раньше, чем парашютист? Сопротивлением воздуха для падающего предмета пренебречь.

Вариант №11 К-Мех.2

1. Сокол-сапсан, пикируя с высоты на свою добычу, достигает скорости 100 м/с. Какое расстояние он при этом проходит? Падение хищника считать свободным.

2. Какую информацию можно получить из графиков скоростей тел? Записать уравнения скорости для первого и второго тела. Начертить графики ускорения для каждого из тел.

3. Почему нельзя говорить о средней скорости переменного движения вообще, а можно говорить только о средней скорости за данный промежуток времени или о средней скорости на данном участке пути?

4. Тело, имея начальную скорость v0 = 2 м/с, двигалось в течение 3 секунды равномерно, затем 2 секунды равноускоренно с ускорением 2 м/с2, затем 5 секунд ускорение было равно 1 м/с2 и наконец 2 секунды равномерно со скоростью, полученной в конце последнего промежутка времени. Найти конечную скорость, пройденный путь и среднюю скорость на всём пути.

Вариант №12 К-Мех.2

1. При подходе к станции поезд уменьшил скорость от 90 до 45 км/ч в течение 25 секунд. Найти ускорение, считая движение равноускоренным.

2. Построить графики скорости для движений, у которых: a) v0x = 0; ax = 2 м/с2; б) v0x = 10 м/с; аx = -2,5 м/с2. Как зависит скорость от времени в каждом случае?

3. На рисунке показан вектор ускорения. Каков характер движения, если тело движется вверх? вниз?

4. По одному направлению из одной точки одновременно начали двигаться два тела: одно – равномерно со скоростью 12 м/с, а другое – равноускоренно без начальной скорости и приобрело за первую секунду своего движения скорость 3 м/с. Через какое время второе тело догонит первое.

Вариант №13 К-Мех.2

1. Свободно падающее тело за 8 секунд приобрело скорость 78,4 м/с. Чему равна начальная скорость этого тела?

2. По графикам ускорений тел, изображенных на рисунке, построить графики скоростей, считая: v01x = 0; v02x = 8 м/с.

3. Уравнение скорости движущегося тела имеет вид vx = 5 + 4t. Каким будет соответствующее уравнение перемещения?

4. Поезд начинает двигаться равноускоренно и за первые 10 секунд проезжает мимо дежурного по вокзалу, находившемуся в начале движения у начала первого вагона. Какую скорость будет иметь состав после прохождения мимо дежурного десятого вагона? Длина каждого вагона 20 м, промежутками между вагонами пренебречь.

Видео:Урок 12. Равномерное прямолинейное движениеСкачать

Вариант №14 К-Мех.2

1. Троллейбус двигался со скоростью 14,4 км/ч. Водитель нажал на тормоз, троллейбус остановился через 4 секунды. Определите ускорение и тормозной путь.

2. По уравнению скорости движения тела vx = 50 -10t, построить графики vx(t) и аx(t).

3. О какой скорости (средней или мгновенной) идёт речь: а) токарь обрабатывает деталь со скоростью резания 3500 м/мин; б) спортсмен на финише имел скорость 10 м/с.

4. Автомобиль, имея скорость 32,4 км/ч, за 22 секунды увеличил её до 72 км/ч. Определить перемещение автомобиля, считая движение равноускоренным.

Видео:Вращательное движение. 10 класс.Скачать

Вариант №15 К-Мех.2

1. Напишите формулу зависимости скорости от времени для случая, когда в начальный момент времени скорость тела 30 м/с, а ускорение равно 2 м/с2. Вычислите скорость тела через 20 секунд от начала отсчёта времени.

2. По условию 1-ой задачи постройте графики зависимости скорости, и ускорения от времени.

3. О какой скорости (средней или мгновенной) идёт речь в следующих случаях: а) скоростемер на самолёте показывает 275 км/ч;

б) трактор засевает поле со скоростью 20 км/ч;

в) на финише спортсмен достиг скорости 2 м/с.

4. С какой высоты свободно упало тело, если за последние 2 с пролетело 60 м? Сколько времени оно падало? Принять g = 10 м/с2.

Видео:Уравнение движенияСкачать

Вариант №16 К-Мех.2

1. С каким ускорением двигался всадник, если его скорость за 15 секунд изменилась от 28,8 до 39,6 км/ч.

2. Построить график скорости для движений, у которых: а) v0x =10 м/с; аx = -2 м/с2; б) v0x = 2 м/с; аx = 2 м/с2. Как зависит скорость от времени в каждом случае?

3. Какие из приведённых зависимостей описывают равноускоренное движение? 1) vx = 23 +2t; 2) Sx = 33 + 2t; 3) Sx = 43t2; 4) Sx = 65t — t2; 5) Sx = 22 — 3t + 4t2; 6) vx = 4.

4. Скорость некоторого тела в момент времени t1 = 3 с равна v1x = 3 м/с, а в момент времени t2 = 6 с скорость тела равна нулю. Определить путь, пройденный телом за 5 с от начала отсчета времени. Тело движется прямолинейно с постоянным ускорением.

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Вариант №17 К-Мех.2

1. Автомобиль прошёл путь 30 м, с каким ускорением он двигался, если его скорость в начальный момент времени была 14,4 км/ч, а в конце пути 10 м/с.

2. В какой момент времени скорость тела равна нулю, если она задана уравнением vx = t, построить график vx(t) и найдите модуль скорости через 5 с, после начала движения.

3. Два самолёта летят на встречных курсах, один с уменьшающейся по модулю скоростью с запада на восток, другой, ускоряясь с востока на запад. Как направлены ускорения самолётов?

4. Мотоциклист, трогаясь с места, едет с ускорением а1 = 2 м/с2. Достигнув скорости 43,2 км/ч, он некоторое время едет равномерно, а затем тормозит с ускорением а2 = 4 м/с2 до остановки. Найти путь, пройденный мотоциклом, если движение продолжалось 30 с.

Видео:Физика. Курс механики | Виды движения. Равномерное движениеСкачать

Вариант №18 К-Мех.2

1. Тело движется из состояния покоя прямолинейно с постоянным ускорением и за 6 секунд проходит 18 м. Определить ускорение.

2. Какую информацию о движении тел можно получить из графиков изображенных на рисунке? Записать уравнения скорости для первого и второго тела.

3. О какой скорости идёт речь в следующем явлении: скорость движения автомобиля между пунктами А и В равна 68 км/ч.

4. Велосипедист скатывается с горы длиной 240 м. С какой скоростью он закончит спуск, если начальная скорость равна 1 м/с, а время спуска длится 2 мин?

Видео:Физика,10-й класс, Равномерное прямолинейное движение. Решение задачСкачать

Вар иант №19 К-Мех.2

1. Автомобиль начал движение прямолинейно с постоянным ускорением 2 м/с2, в некоторый момент времени его скорость равна 10 м/с. Какое перемещение совершил автомобиль за это время?

2. Уравнения движения тел имеют вид: x1 = 3; x2 = 5 + 0,2t2; x3 = 2t — 3t2; x4 = 8 — 2t + 0,5t2. Напишите уравнения зависимости скорости каждого из тел от времени.

3. По графикам скорости, изображенным на рисунке, определите ускорения тел. Каков характер их движения?

4. Материальная точка движется из состояния покоя в конце второй секунды ее скорость 10 см/с. Какую скорость будет иметь материальная точка в момент прохождения координаты 100 см. Принять начальную координату точки x0 = -10 см.

Видео:Прямолинейное движение. 10 класс.Скачать

Вариант №20 К-Мех.2

1. При посадке самолёт коснулся посадочной полосы аэродрома при скорости 70 м/с. Через 20 с он остановился. Определить ускорение при движении самолета по посадочной полосе.

2. По графикам ускорения, приведенным на рисунке, дайте характеристику движения каждого тела, если v01 = 0, а v02 = 2 м/с.

3. Два камешка выпущены из рук, с одной и той же высоты, один после другого через 1 с. По какому закону будет меняться расстояние между ними при дальнейшем их падении?

4. Автомобиль двигаясь равномерно перешел на равноускоренное движение с ускорением 2 м/с2, прошёл путь 250 м за 10 с. Какова конечная скорость?

Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Вариант №21 К-Мех.2

1. Скорость тела в конце десятой секунды равна 15 м/с. Какова была скорость в конце пятой секунды, если движение было равноускоренным и началось из состояния покоя?

2. По графикам ускорений построить графики скоростей. Считать v01 = 2 м/с, а v02 = 6 м/с.

3. Тело за первую секунду прошло 1 м, за вторую 2 м, за третью 3 м и так далее. Является ли такое движение равноускоренным?

4. Поезд, трогаясь с места, движется с ускорением а1 = 1,5 м/с2. Достигнув скорости 36 км/ч, он некоторое время едет равномерно, а затем тормозит с ускорением а2 = 3 м/с2 до остановки. Найти время движения поезда, если он прошёл путь 500 м.

Видео:Закон Сложения Скоростей - Относительная скорость / Урок Физики 10 класс / КинематикаСкачать

Вариант №22 К-Мех.2

1. Сколько времени необходимо комбайну двигаясь из состояния покоя с ускорением 1 м/с2 для приобретения скорости 25,2 км/ч.

2. По графикам изображенным на рисунке определить ускорение тел и напишите выражения зависимости скорости, и перемещения этих тел от времени.

3. Как будет изменяться плотность дождя (количество капель в 1 м3), по мере приближения к поверхности Земли?

4. Поезд, движущийся после начала торможения с ускорением 0,4 м/с2, через 25 с остановился. Найти тормозной путь.

Видео:Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Вариант №23 К-Мех.2

1. Сани спускаются с горы 8 с. Начальная скорость саней 2 м/с, ускорение 40 см/с2. Определить скорость саней у подножия горы.

2. Построить графики зависимости скорости и ускорения от времени для двух тел: а) v01 = 45 м/с; а1 = -5 м/с2; b) v02 = 10 м/с; а2= 2 м/с2.

3. Почему нельзя говорить о средней скорости переменного движения вообще, а можно говорить только о средней скорости за данный промежуток времени или о средней скорости на данном участке пути?

4. В одном направлении из одной точки одновременно начали двигаться два тела: одно – равномерно со скоростью 16 м/с, а другое – равноускоренно, приобрело за первую секунду своего движения скорость 4 м/с. За какое время второе тело догонит первое.

Вариант №24 К-Мех.2

1. Тело движется равнозамедленно с ускорением ах=-2 м/с2. На каком расстоянии от исходной точки будет тело через 5 с после начала отсчета времени, если начальная скорость равна 10 м/с?

2. Скорость задана уравнением vx =-3 + 6t, построить график скорости и найти ее модуль через 5 с, после начала отсчета времени. В какой момент времени скорость тела была равна нулю?

3. Можно ли по данным за несколько минут, снятым через каждую минуту во время езды на автомобиле, определить среднюю скорость движения за все время езды на автомобиле?

4. Аэростат спускается с постоянной скоростью 5 м/с. На расстоянии 50 м от земли из него выпал маленький и тяжелый предмет. На сколько позже приземлится аэростат, чем этот предмет? Сопротивлением воздуха для падающего предмета пренебречь.

Вариант №25 К-Мех.2

1. По полу равнозамедленно движется шар, с начальной скоростью 0,64 м/с и ускорением 16 см/с2. Какой путь он пройдёт до остановки?

2. Построить графики зависимости скорости и ускорения от времени, если: v0x = 500 м/с; аx = -50 м/с2.

3. Два тела брошены вниз: одно – без начальной скорости, второе — с начальной скоростью. Что можно сказать об ускорениях этих тел? Сопротивление воздуха не учитывать.

4. Тело движется равноускоренно и в шестую секунду проходит 12 м. Определить ускорение и скорость после десяти секунд движения, если начальная скорость была равна нулю.

Вариант №26 К-Мех.2

1. Аэросани за 8 с прошли 40 м, с ускорением 1 м/с2. Чему равна начальная скорость?

2. По графику дайте характеристику движения для тел (а) и (b) изображенных на рисунке. Напишите уравнения зависимости скорости от времени для каждого тела, считая начальную скорость тел равной нулю.

3. В момент времени t = 6 с, скорость самолёта равна 230 км/ч, о какой скорости идёт речь?

4. Автомобиль двигался по прямолинейному участку дороги с постоянной скоростью 72 км/ч. На расстоянии 48,5 м от светофора водитель нажал на тормоз. Через 4 с после этого скорость стала 4 м/с. Найдите положение автомобиля относительно светофора.

Вариант №27 К-Мех.2

1. По уравнению скорости движения тела vx = 15 + 8t, найти его перемещение за 10 с.

2. Построить графики зависимости скорости и ускорения от времени, если v0 = 400 м/с, а = -25 м/с2.

3. О какой скорости (средней или мгновенной) идёт речь в следующих случаях: а) рота солдат движется со скоростью 5 км/ч;

б) спидометр автомобиля показывает 75 км/ч;

в) при вылете из автомата скорость пули 500 м/с.

4. Состав двигался со скоростью 72 км/ч. Найти время торможения, если тормозной путь равен 800 м?

Вариант №28 К-Мех.2

1. Какое расстояние прошёл автобус, если его начальная скорость была 7,2 км/ч, а конечная 10 м/с, и двигался с ускорением 1 м/с2.

2. По графику изображенному на рисунке определить ускорения тел, напишите выражения для скорости и перемещения этих тел.

3. О какой скорости идёт речь: во время попадания в мишень стрела имела скорость 3 м/с.

4. Аэросани за 8 с прошли 40 м, с ускорением 1 м/с2. Чему равна приобретённая санями скорость?

Вариант №29 К-Мех.2

1. Тело свободно падает без начальной скорости. Какую максимальную скорость оно может иметь, если высота падения 10 м?

2. Построить графики скорости для движения двух тел, у которых: а) v01 = 2 м/с; а1 = 0; b) v02 = 0; а2 = 2 м/с2. Как зависит скорость от времени в каждом случае?

3. В каком случае путь, пройденный за первую секунду, в равнопеременном движении численно не равен половине ускорения?

4. Самосвал, двигаясь под уклон, прошёл за 20 с путь 340 м и развил скорость 24 м/с. Считая движение равноускоренным, найти ускорение самосвала и его скорость в начале уклона.

Вариант №30 К-Мех.2

1. Автобус скорость которого 5 м/с, начал двигаться с постоянным по модулю ускорением 0,5 м/с2, направленным в ту же сторону, что и вектор скорости. Определите скорость автомобиля через 15 с.

2. Скорость задана уравнением vx = 16 + 2t, построить графики зависимости скорости и ускорения от времени. Написать уравнение зависимости x(t), считать x0=40 м.

3. На рисунке показан вектор ускорения. Каков характер движения, если тело движется влево? вправо?

4. Стрела, летящая со скоростью 50 м/с, попадает в деревянную доску. Найдите глубину проникания стрелы, если она двигалась в дереве 0,005 с. Движение в дереве считать равноускоренным. С каким ускорением двигалась стрела в дереве?

Уравнение координаты при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Уравнение координаты — зависимость координаты тела от времени:

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.

Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x₀ = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с 2 . Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v₀ = 0 м/с.

В момент времени t = 10 c координата автомобиля равна:

Совместное движение двух тел

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

1. Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
2. Построить уравнение вида x₁ = x₂.
3. Найти время встречи двух тел t_встр.
4. Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату x_встрч.

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

x = 3t = 3∙6 = 18 (м).

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

1. Построить графики x1(t) и x2(t).
2. Найти точку пересечения графиков.
3. Пустить перпендикуляр из этой точки к оси ОХ.
4. Значение точки пересечения — координата места пересечения двух тел.

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с 2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с 2 , достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:

В результате получаем два

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.

В момент времени t=0 проекции её скорости υ_x и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

Алгоритм решения

1. Определить характер движения материальной точки.
2. Записать уравнение координаты материальной точки.
3. С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.

Решение Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

1. Записать исходные данные.
2. Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
3. Выразить скорость грузовика из уравнения его движения.
4. Записать уравнение движения мотоциклиста.
5. Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
6. Подставить время в формулу скорости грузовика и вычислить ее.

Решение

• Координата встречи грузовика и мотоциклиста: x = 150 м.
• Время запаздывания мотоциклиста: t_запазд = 5 с.
• Ускорение, с которым мотоциклист начал движение: a = 3 м/с 2 .

Запишем уравнение движения грузовика:

Так как начальная координата равна нулю, это уравнение примет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Отсюда скорость движения грузовика равна:

Запишем уравнение движения мотоциклиста:

Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:

Найдем время, через которое грузовик и мотоциклист встретились:

Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:

pазбирался: Алиса Никитина | обсудить разбор | оценить