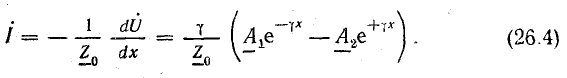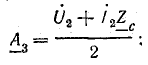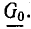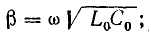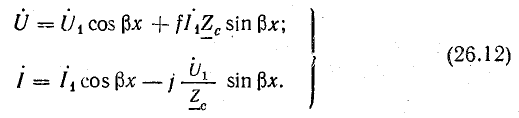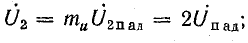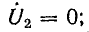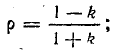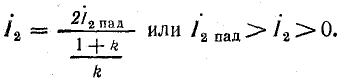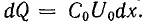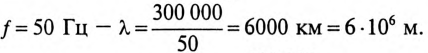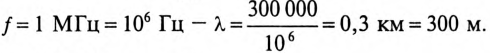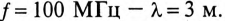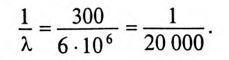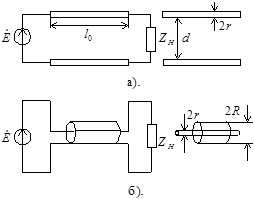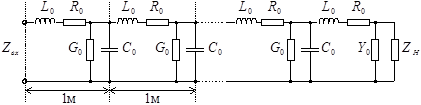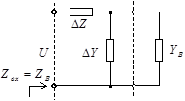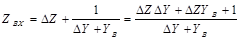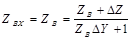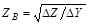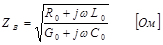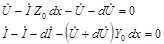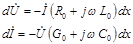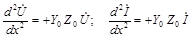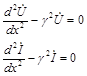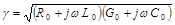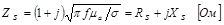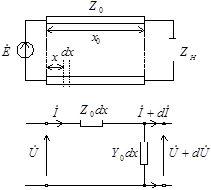Содержание:
Электрические цепи с распределенными параметрами:
Каждый элемент электрической цепи (резистор, катушка, конденсатор) имеет конечные размеры, и его можно представить как совокупность малых однородных частей, в которых совершаются интересующие нас электромагнитные процессы — преобразование энергии в тепло, накопление энергии в магнитном и электрическом полях. Иначе говоря, все устройства имеют распределенные параметры — сопротивление, индуктивность, емкость.
При изучении электрических цепей до сих пор мы не учитывали размеры устройств, предполагая, что параметры R, L, C сосредоточены, т. е. представляли в расчетной схеме каждый элемент в целом.
Такой подход к анализу электрических цепей принимают тогда, когда рассматривают и изучают внешние связи между элементами. В тех случаях, когда требуется выявить соотношения внутри устройства, соответствующий элемент рассматривается как объект с распределенными параметрами. Таким объектом может быть обмотка электрической машины, трансформатора, антенна радиотехнического устройства и др.
- Электрическая цепь с распределенными параметрами
- Уравнения длинной линии
- Схемы замещения длинных линий
- Основные уравнения длинной линии
- Характеристики длинной линии
- Установившийся режим в длинной линии без потерь
- Уравнения длинной линии без потерь
- Холостой ход
- Короткое замыкание
- Стоячая волна
- Бегущая волна
- Волновое сопротивление. Длина волны
- Нагрузочные режимы длинной линии без потерь
- Режим с согласованной нагрузкой
- Режим с несогласованной нагрузкой
- Коэффициенты отражения и преломления
- Распространение электромагнитной волны с прямоугольным фронтом по линии без потерь
- Электромагнитная волна с прямоугольным фронтом
- Подключение источника постоянного напряжения U0 к бесконечно длинной линии
- Включение источника постоянного напряжения на линию конечной длины
- Электрические цепи с распределенными параметрами
- Уравнения длинных линий
- Длинная линия
- Длинная линия
- Содержание
- Дифференциальные уравнения длинной линии
- Погонные параметры
- Эквивалентная схема участка длинной линии
- Телеграфные уравнения
- Условие регулярности линии
- Однородные волновые уравнения длинной линии
- Распределение поля падающей волны
- Комплексный коэффициент отражения по напряжению
- Коэффициенты бегущей и стоячей волны
- Входное сопротивление длинной линии
- Режимы работы длинной линии
- Режим бегущей волны
- Режим стоячей волны
- Режим смешанных волн
- 🎦 Видео
Видео:Распространение и взаимодействие волн в длинных линияхСкачать

Электрическая цепь с распределенными параметрами
Электрическая цепь с распределенными параметрами — это цепь, в которой сопротивления, проводимости, индуктивности и емкости распределены вдоль цепи.
Наглядным примером цепи с распределенными параметрами является электрическая длинная линия.
Уравнения длинной линии
Длинные линии строят для передачи электрической энергии, для электросвязи (передачи информации). Их рассматривают как объекты с распределенными параметрами при низких частотах и длине в десятки и сотни километров.
В радиотехнике при высоких частотах распределение параметров по длине учитывают в более коротких участках проводов (единицы и доли метра), например в антеннах.
Схемы замещения длинных линий
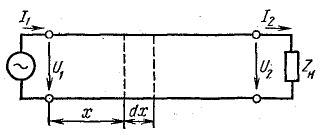
На рис. 26.1 изображена схема электрической цепи, состоящей из источника и приемника электрической энергии, связанных двухпроводной линией. Эту цепь можно рассматривать неразветвленной, с одинаковым током во всех ее элементах, если не учитывать двух обстоятельств: скорость распространения электромагнитных возмущений конечна; имеются токи, обусловленные емкостью между проводами (емкостный ток) и проводимостью изоляции (ток утечки через изоляцию).
В данном случае первое обстоятельство можно не учитывать, так как скорость распространения электромагнитных возмущений действительно велика (в вакууме равна скорости света). Емкостные токи и токи утечки пропорциональны напряжению между проводами; кроме того, емкостный ток увеличивается с ростом частоты, так как уменьшается емкостное сопротивление. Поэтому при высоком напряжении или большой частоте, а также при большой длине линии емкостные токи и токи утечки становятся значительными по величине и их нельзя исключить из расчета.
Токи между проводами существуют на сколь угодно малом отрезке линии, поэтому ток в проводах уменьшается по мере удаления от начала линии.
Вдоль линии напряжение между проводами тоже неодинаково. Оно уменьшается в направлении от начала к концу линии, так как растет падение напряжения, обусловленное активным и индуктивным сопротивлениями проводов.
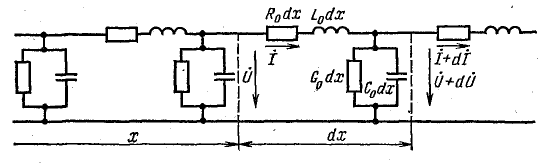
Для расчета можно составить схему замещения линии, изображенную на рис. 26.2. На схеме замещения бесконечно малый участок двухпроводной линии длиной dx представлен ячейкой с активным сопротивлением R0dx прямого и обратного проводов, индуктивностью L0dx, проводимостью G0dx и емкостью C0dx между проводами. Вся линия изображается электрической схемой последовательного соединения таких ячеек. Активное сопротивление, индуктивность, проводимость и емкость считают равномерно распределенными вдоль линии, а R0, L0, G0, C0 — величины этих параметров на единицу длины.
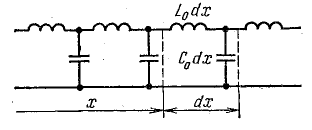
Рис. 26.3. Схема замещения однородной линии без потерь
Линия с равномерным распределением параметров называется однородной. Реальные линии можно считать однородными лишь приближенно, так как параметры их все же распределены неравномерно. Например, проводимость воздушной линии сосредоточена в основном на опорах, а благодаря провесу проводов емкость по отношению к земле вдоль пролета неодинакова.
В зависимости от целей и требуемой точности расчета можно учитывать все четыре параметра или некоторые из них. Так, при рассмотрении линии электропередачи с напряжением до 35 кВ и при частоте 50 Гц часто не учитывают емкостные токи и токи утечки, т. е. считают равными нулю параметры C0 и G0.
При высокой частоте (например, в радиотехнических устройствах) или при коротких импульсах напряжения в линиях, возникающих от грозовых разрядов, емкостные токи между проводами могут быть сравнительно большими и ими пренебрегать нельзя.
Вместе с тем при высокой частоте и малой длине линии в отдельных случаях можно пренебречь активным сопротивлением R0 и проводимостью G0.
При таком упрощении получается линия без потерь, схема замещения которой показана на рис. 26.3.
Основные уравнения длинной линии
При синусоидальном напряжении источника питания напряжение и ток в линии на любом расстоянии x от ее начала изменяются во времени. Вместе с тем напряжение и ток изменяются вдоль линии. Установившийся режим в длинной линии представляется довольно сложной пространственно-временной картиной, для изучения которой необходимо получить аналитическую зависимость напряжения и тока от двух независимых переменных — времени и расстояния.
Решить такую задачу можно, используя схему замещения однородной линии (см. рис. 26.2). На схеме кроме параметров некоторого элемента длины линии dx обозначены напряжение и ток в начале и конце этого элемента, расположенного на расстоянии x от начала линии.
Падение напряжения в элементе длины dx линии 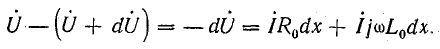
Разность токов в начале и конце того же элемента равна сумме тока утечки и емкостного тока: 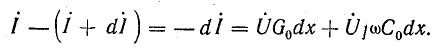
Из этих выражений получают дифференциальные уравнения однородной линии, в которые входят комплексы токов и напряжений, изменяющихся во времени по синусоидальному закону, а также их производные по переменной координате х: 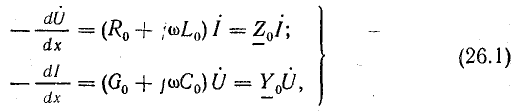
где 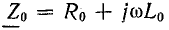
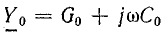
Продольные R0, L0 и поперечные G0, C0 параметры линии характеризуют совершенно различные физические явления, поэтому между собой не связаны.
Далее можно составить уравнения, в которых переменными будут напряжение или ток. Для этого продифференцируем по х уравнения (26.1): 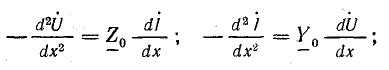
учитывая выражения (26.1), получим линейные дифференциальные уравнения второго порядка с постоянными коэффициентами: 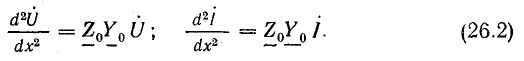
Решением первого уравнения из (26.2) является выражение 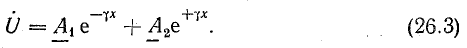
Уравнение тока получим из (26.1) и (26.3):
Характеристики длинной линии
В выражениях (26.3) и (26.4) 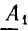
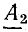
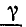
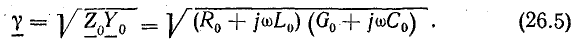
Учитывая формулу (26.5), запишем другое уравнение тока: 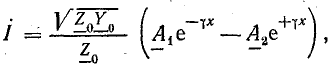
или 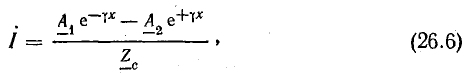
где величина 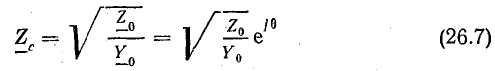
имеет размерность сопротивления и называется волновым сопротивлением линии.
Постоянные коэффициенты 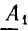
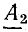
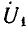
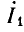
Из уравнений (26.3) и (26.6) при x = 0 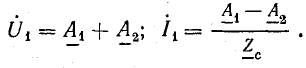
Отсюда 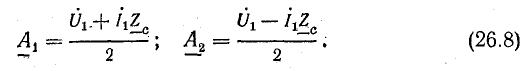
Отношение комплекса напряжения к комплексу тока в начале линии называется входным сопротивлением линии.
Входное сопротивление линии при нагрузке 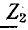
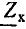
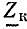
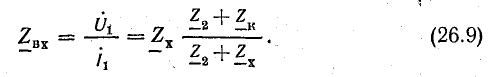
Коэффициент распространения электромагнитной волны 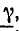
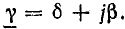
Этот коэффициент, имея два слагаемых, характеризует две стороны электромагнитного процесса в линии: затухание амплитуд и изменение фазы напряжения и тока в зависимости от расстояния от начала линии.
В соответствии с этим действительная часть комплекса δ называется коэффициентом затухания, а мнимая часть β — коэффициентом фазы.
Коэффициент затухания δ показывает степень затухания амплитуды колебаний при распространении волны на единицу длины.
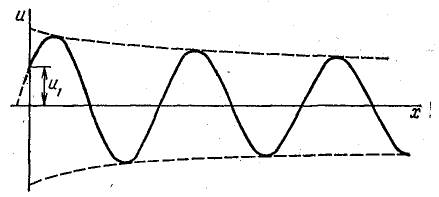
Рис. 26.4. График распределения напряжения вдоль линии
На рис. 26.4 показан график распределения напряжения вдоль линии в некоторый фиксированный момент времени. Из графика видно, что напряжение вдоль линии распределено по периодическому закону, а амплитуды напряжения затухают по экспоненциальному закону в направлении от начала к концу линии.
Задача 26.1.
Трехфазная линия электропередачи длиной l = 900 км имеет первичные параметры: R0 = 0,08 Ом/км; Z0 = 1,336 • 10 -3 Гн/км; С0 = 8,6 x 10 -9 Ф/км; G0 = 3,75 • 10 -8 См/км.
Нагрузка в конце линии Р2 = 300 МВт; U2 = 380 кВ; соsφ2 = 1; частота f = 50 Гц.
Определить вторичные параметры линии (Zc, γ), напряжение и ток на ее входе.
План решения:
1. Комплексы «продольного» сопротивления и «поперечной» проводимости [см. формулы (26.1)].
2. Волновое сопротивление линии — по формуле (26.7).
3. Коэффициент распространения — по формуле (26.5).
4. Коэффициент затухания и коэффициент фазы — по формуле 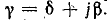
5. Ток в конце линии — по формуле (20.9).
6. Напряжение и ток в начале линии — по формулам (26.3) и (26.6), которые следует записать при условии, что расстояния вдоль линии отсчитываются от конца линии: 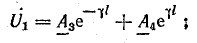
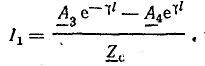
При этом 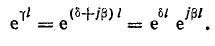
Коэффициенты 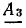
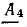
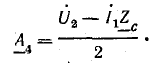
Выполнить вычисления по данному плану.
Установившийся режим в длинной линии без потерь
Линия без потерь, как уже было отмечено, не имеет активных сопротивления R0 и проводимости
В радиотехнике длинные линии с малыми потерями встречаются часто, поэтому рассмотрение линии при R0 = 0 и G0 = 0 имеет практическое значение.
Уравнения длинной линии без потерь
Согласно формулам (26.5) и (26.9), для линии без потерь коэффициент затухания 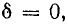
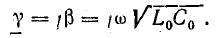
Поэтому график распределения напряжения вдоль линии в некоторый фиксированный момент времени представляет собой синусоиду. Амплитуда напряжения вдоль линии остается постоянной (рис. 26.5). Волновое сопротивление [см. формулу (26.7)] 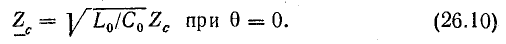
Уравнения напряжения и тока в линии без потерь, согласно уравнениям (26.3), (26.6), 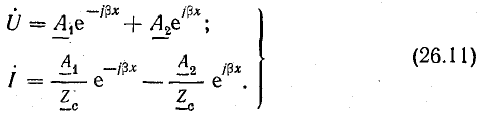
Вместо коэффициента 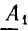
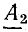
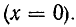
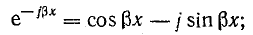
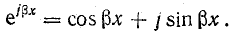
После преобразования из уравнений (26.11) получим
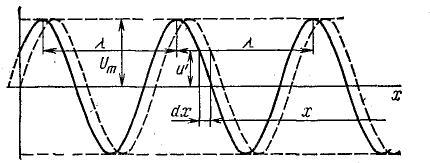
Рис. 26.5. Распределение волны напряжения вдоль линии без потерь
Из этих уравнений можно также получить выражения напряжения и тока в любой точке линии, если известны напряжение U2 и ток I2 в конце линии, при условии отсчета расстояния от конца линии: 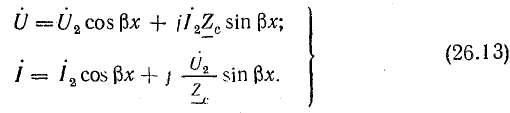
С помощью уравнений (26.12) и (26.13) можно исследовать различные режимы длинной линии без потерь.
Холостой ход
При холостом ходе линии (I2 = 0) 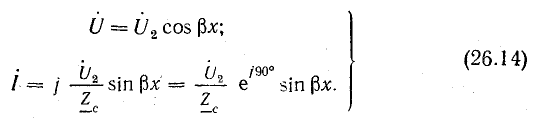
Напряжение и ток вдоль линии в любой момент времени распределены по синусоидальному закону, причем в пунктах, где напряжение равно нулю, ток имеет наибольшую величину, а в пунктах с наибольшим напряжением ток равен нулю (рис. 26.6, а, б).
Точки линии, в которых напряжение или ток равны нулю, называются узлами, а точки с наибольшей величиной напряжения или тока — пучностями.
Таким образом, узлы напряжения по месту расположения на линии совпадают с пучностями тока, а пучности напряжения — с узлами тока.
Положение узлов напряжения и пучностей тока найдем, приравняв нулю напряжение в первом уравнении (26.14): U = 0 при 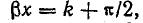
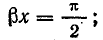
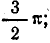
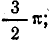
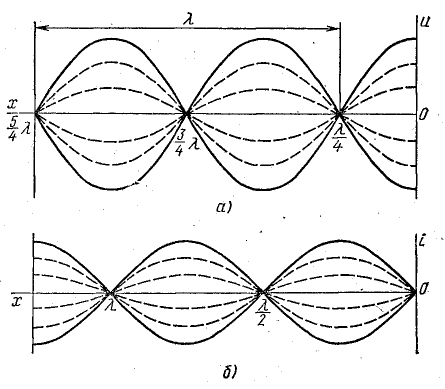
Рис. 26.6. Графики напряжения и тока стоячей электромагнитной волны в длинной линии без потерь
Положение на линии узлов тока и пучностей напряжения определяется из второго уравнения (26.14) при I = 0.
Напряжение и ток, распределяясь вдоль линии по синусоидальному закону без затухания, по такому же закону изменяются во времени.
Короткое замыкание
Аналогичная картина наблюдается и при коротком замыкании конца линии без потерь. Отличие электромагнитных процессов в линии без потерь в режимах холостого хода и короткого замыкания состоит лишь в том, что изменяется расположение пучностей и узлов напряжения и тока по длине линии: в тех пунктах, где при холостом ходе находятся пучности напряжения и узлы тока, при коротком замыкании обнаруживаются пучности тока и узлы напряжения. В частности, в конце разомкнутой линии имеется пучность напряжения и узел тока 
Стоячая волна
Пусть вектор напряжения в конце разомкнутой линии направлен по действительной оси комплексной плоскости, т. е. начальная временная фаза напряжения равна нулю:
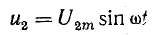
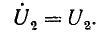
В этом случае мгновенные значения напряжения и тока в линии можно выразить уравнениями 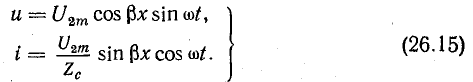
При 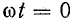
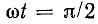
Но эта амплитуда напряжения во всех пунктах линии разная. В месте пучности напряжение достигает наибольшей величины U2m, а в узле она всегда равна нулю.
Электромагнитный процесс, подчиняющийся уравнениям (26.15), называется стоячей волной, характерной особенностью которой является неподвижность узлов и пучностей на линии.
Бегущая волна
Из тригонометрии известно, что 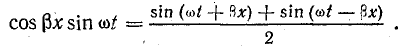
Следовательно, напряжение и ток в линии можно представить суммой двух составляющих, каждая из которых является уравнением бегущей волны: 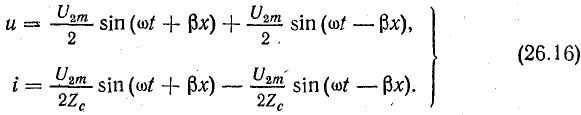
Первое слагаемое в этих уравнениях — прямая волна, распространяющаяся от начала к концу линии; второе — обратная волна с такой же амплитудой.
В этом можно убедиться, рассмотрев подробно одну из составляющих, например первую в уравнении напряжения.
Предположим, что некоторая величина напряжения u’ в момент времени t имеет место в пункте, пространственное положение которого определяется расстоянием x от конца (или начала) линии (см. рис. 26.5): 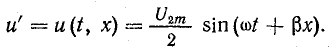
Распространение волны напряжения означает, что через бесконечно малый промежуток времени dt такое же напряжение u’ возникает в другом пункте линии, отстоящем от первого на бесконечно малое расстояние dx: 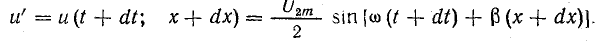
Равенство напряжений в моменты времени, отстоящие на dt, возможно при равенстве аргументов синусов в обоих уравнениях, т. е. при 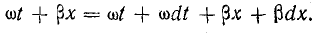
Отсюда 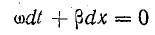
или 
Отношение 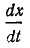
Знак минус указывает на то, что волна движется от начала к концу линии (расстояние x уменьшается).
Аналогично можно показать, что вторая составляющая напряжения в уравнении (26.16) представляет собой волну, распространяющуюся в обратном направлении (x увеличивается).
Волна, распространяющаяся от начала к концу линии, называется прямой или падающей, а волна, распространяющаяся в обратном направлении (от конца линии к началу), — обратной или отраженной.
Те же рассуждения можно отнести к составляющим тока во втором уравнении (26.16).
Таким образом, стоячая волна напряжения представляет собой сумму, а волна тока — разность прямой (падающей) и обратной (отраженной) волн одинаковой амплитуды.
Волновое сопротивление. Длина волны
Уравнения (26.16) запишем в таком виде: 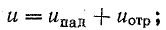
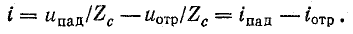
Отсюда 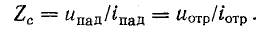
Волновое сопротивление линии выражается отношением напряжения к току падающих волн или аналогичным отношением для отраженных волн.
Волновое сопротивление линии можно определить через входные сопротивления при холостом ходе и коротком замыкании: 
Большой интерес представляет также расстояние, на которое бегущая волна распространяется за время одного периода синусоидально изменяющегося напряжения или тока.
Из формулы (26.17) видно, что фазовая скорость постоянна, поэтому 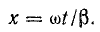
Путь, пройденный волной за время периода 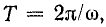
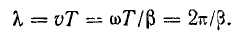
В линии без потерь фазовая скорость 
а длина волны 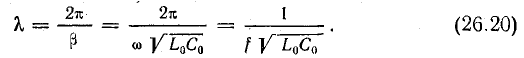
Найдем величину фазовой скорости для воздушной линии без потерь, подставляя в формулу (26.19) L0 и С0 двухпроводной линии, определенные ранее [см. формулы (7.31), (8.29)]: 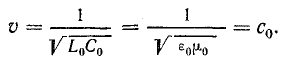
Фазовая скорость электромагнитной волны в воздушной линии без потерь равна скорости света.
Если среда, в которой распространяется электромагнитная волна, характеризуется величинами диэлектрической 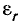
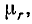
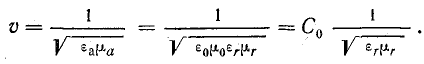
Принимая 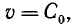
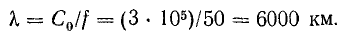
Нетрудно заметить, что при частоте 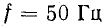
В линиях дальних передач с номинальным напряжением 500 кВ и более изменения величины напряжения вдоль линии становятся заметными и приходится принимать меры к его выравниванию. С увеличением частоты длина волны уменьшается. В технике связи, где применяются высокие частоты, длина волны может быть во много раз меньше длины линии.
Задача 26.3.
В конце двухпроводной линии без потерь напряжение U2 = 600 В при холостом ходе. Определить напряжение и ток в начале линии, если известны: волновое сопротивление 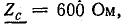
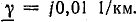
План решения.
1. Напряжение в начале линии по первой формуле (26.13) при I2 = 0.
2. Ток в начале линии по второй формуле (26.13).
Выполнить подсчеты по данному плану.
Дополнительное задание: определить напряжение и ток в начале линии при коротком замыкании на конце, где ток I = 4 А.
Нагрузочные режимы длинной линии без потерь
Кроме крайних режимов холостого хода и короткого замыкания для практики еще более интересными являются нагрузочные режимы, когда в конце линии включается приемник электромагнитной энергии. Из различных нагрузочных режимов рассмотрим режимы с согласованной и несогласованной активными нагрузками.
Режим с согласованной нагрузкой
Режим в линии называется согласованным, если сопротивление нагрузки в конце линии равно ее волновому сопротивлению: 
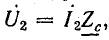
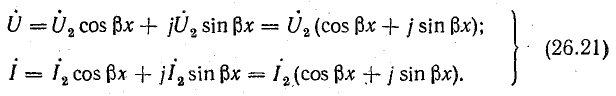
Учитывая, что 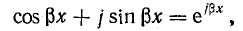
уравнения (26.21) можно записать в виде 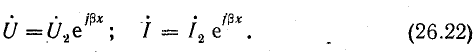
Предположим, что синусоидальное напряжение в конце линии имеет начальную фазу ψ = 0, тогда 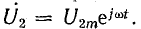
Если нагрузка линии активная (R2 = Zc), ток и напряжение совпадают по фазе: 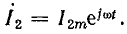
Уравнения напряжения и тока в линии: 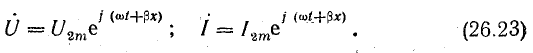
В этом случае мгновенные величины напряжения и тока в любом пункте линии на расстоянии x от ее концов определяются уравнениями 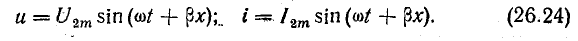
Это уравнения бегущих волн напряжения и тока, распространяющихся от начала к концу линии (прямые волны) с фазовой скоростью 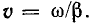
При согласованной нагрузке отраженных волн в линии нет, следовательно, энергия, которую несет падающая электромагнитная волна, полностью поглощается в нагрузке.
Режим с несогласованной нагрузкой
Нагрузка линии называется несогласованной, если нагрузочное сопротивление в конце линии 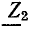
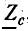
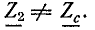
Рассмотрим случай, когда линия замкнута на активное сопротивление 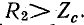
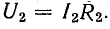
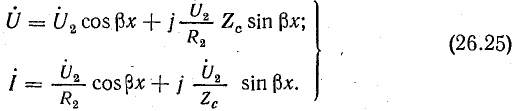
Отношение 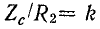
С введением этого коэффициента уравнения (26.25) принимают следующий вид: 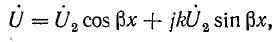
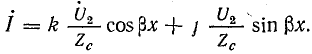
Вместо 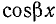
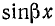
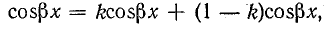
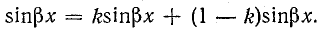
После подстановки получим 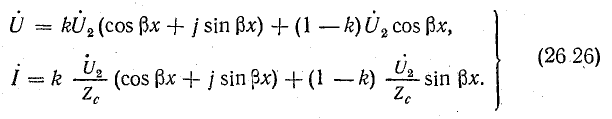
Первые слагаемые в этих уравнениях аналогичны уравнениям (26.21). Анализ их ранее показал, что они выражают бегущие волны напряжения и тока. Вторые слагаемые аналогичны уравнениям (26.14), которые являются уравнениями стоячих волн. Опуская промежуточные выводы, выполненные ранее для бегущих и стоячих волн, напишем уравнения для мгновенных величин напряжения и тока при несогласованной нагрузке: 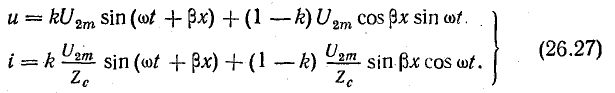
Таким образом, режим в линии без потерь при несогласованной нагрузке можно рассматривать как наложение бегущих и стоячих волн напряжения и тока.
Наличие бегущих волн в направлении от начала к концу линии указывает на потребление энергии в нагрузке. Однако потребляется лишь часть энергии электромагнитной волны, другая часть отражается от конца линии.
Режимы холостого хода и с согласованной нагрузкой линии без потерь являются частными случаями, соответствующими значениям коэффициента бегущей волны k = 0 (холостой ход) и k = 1 (согласованная нагрузка).
Коэффициенты отражения и преломления
Представление электромагнитного процесса в линии как наложение прямых (падающих) и обратных (отраженных) волн напряжения и тока возможно не только в рассмотренных частных случаях. Оно соответствует общим уравнениям напряжения и тока в линии (26.12), в правой части которых записана сумма (разность) двух составляющих.
При анализе электромагнитных процессов в длинных линиях вводится понятие о коэффициенте отражения р, который равен отношению комплекса напряжения отраженной волны к комплексу напряжения падающей волны или аналогичному отношению комплексов токов: 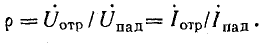
Выразим напряжение и ток в конце линии их падающими и отраженными составляющими в соответствии с уравнениями (26.11): 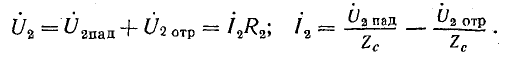
При совместном решении этих уравнений найдем коэффициент отражения: 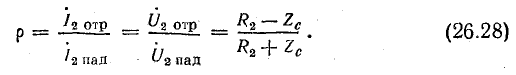
Подставим найденное выражение ρ в уравнения напряжения U2 и тока I2: 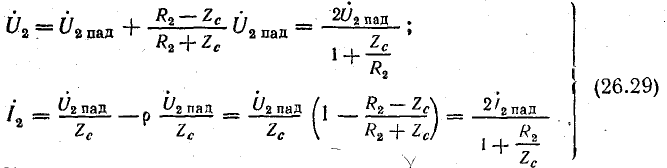
Множители 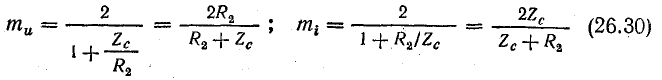
называются коэффициентами преломления волн напряжения (тока).
Согласно выражениям (26.29), коэффициент преломления равен отношению комплексов напряжения (тока) в рассматриваемом пункте линии к комплексу напряжения (тока) падающей волны: 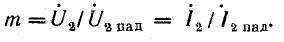
Анализ этих формул показывает:
1) при холостом ходе линии 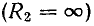

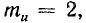
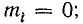
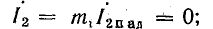
2) при коротком замыкании линии 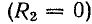
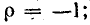
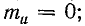
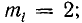
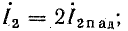
3) при согласованной нагрузке 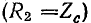
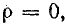
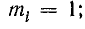
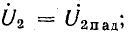
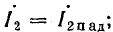
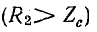
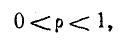
где k — коэффициент бегущей волны; 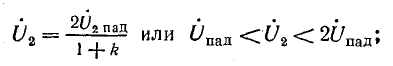
Распространение электромагнитной волны с прямоугольным фронтом по линии без потерь
Как было показано в предыдущих параграфах, установившийся режим в длинной линии при синусоидальном изменении напряжения и тока удобно представить наложением прямых и обратных электромагнитных волн.
Переходные процессы в цепях с распределенными параметрами тоже рассматриваются как движение прямых и отраженных волн, возникающих после включения или отключения какого-либо участка, при передаче телемеханических или телефонно-телеграфных сигналов по линиям связи т. п.
Переходные процессы могут быть также следствием изменения внешних магнитных и электрических полей, связанным с грозовыми явлениями.
Электромагнитная волна с прямоугольным фронтом
В цепи с сосредоточенными параметрами переходный процесс начинается и протекает одновременно во всех ее элементах. Особенностью переходного процесса в длинной линии является то, что появившееся в некоторой точке возмущение распространяется по линии с определен-ной скоростью, поэтому переходный процесс в данном пункте линии начинается тем позднее, чем он дальше от места возмущения.
При переходных процессах в цепях с распределенными параметрами (линии, обмотки электрических машин и трансформаторов) могут возникать электромагнитные волны различной формы.
Качественную сторону явления распространения электромагнитной волны рассмотрим на примере волны с прямоугольным фронтом (рис. 26.7) в линии без потерь.
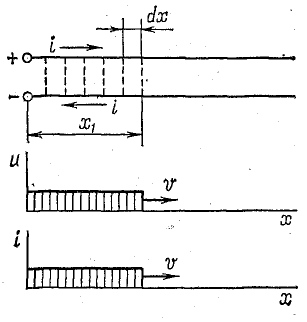
Рис. 26.7. Распределение электромагнитной волны с прямоугольным фронтом вдоль линии без потерь
Для такой волны характерно то, что во всех пунктах линии, расположенных до фронта волны, напряжение и ток равны нулю, а в пунктах линии, расположенных за фронтом волны, напряжение и ток постоянны.
Распространение электромагнитной волны с прямоугольным фронтом означает, что напряжение и ток последовательно в каждом пункте линии изменяются скачком. Как было показано ранее, такое изменение напряжения и тока в цепях, обладающих емкостью и индуктивностью, невозможно, так как требует источника бесконечно большой мощности. Таких источников не существует, поэтому волну с прямоугольным фронтом нужно рассматривать как некоторую идеализацию реального процесса.
Электрические и магнитные явления в линии — это две стороны единого электромагнитного процесса. Однако эти явления удобно рассматривать отдельно, т. е. выделять из электромагнитной волны волну напряжения и волну тока.
Были записаны в комплексной форме уравнения (26.1) для синусоидального изменения напряжения и тока. Те же уравнения для мгновенных величин напряжения и тока в однородной линии без потерь имеют вид 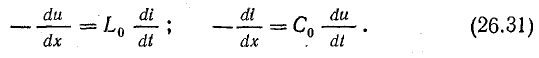
Решением этих уравнений в общем виде являются функции 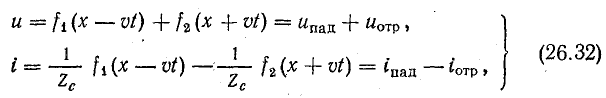
где 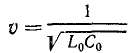
Уравнения (26.32) по своей структуре подобны уравнениям (26.16), поэтому любой электромагнитный переходный процесс в линии можно рассматривать как наложение прямых и обратных волн напряжения и тока. Физический смысл переходных процессов в линии удобно выяснить на простейших примерах.
Подключение источника постоянного напряжения U0 к бесконечно длинной линии
После включения источника вдоль линии будет распространяться волна с прямоугольным фронтом, заряжающая ее последовательно (от одного пункта к другому) до напряжения U0. На поверхности проводов появляется заряд, величина которого на единице длины Q0 = C0U0.
Если за время dt волна переместилась на расстояние dx, линия получает дополнительный заряд
Этот заряд как бы распространяется по проводам от источника вдоль линии до точки х1, в которой находится в данный момент фронт волны; при этом образуется ток 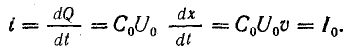
Один провод заряжается положительно, а другой (обратный) — отрицательно, что соответствует противоположному направлению токов в них (рис. 26.7).
На отрезке линии длиной dx, около фронта волны, возникновение электрического поля сопровождается током смещения между проводами. Таким образом, цепь оказывается замкнутой. При движении волны она удлиняется, но ток остается постоянным, равным I0.
Контур, по которому замыкается ток, пронизывается магнитным потоком, направленным, согласно правилу буравчика, в плоскостях, перпендикулярных осям проводов.
Перемещение волны на dx сопровождается увеличением магнитного потока на величину 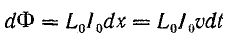
и наведением в контуре э. д. с. самоиндукции 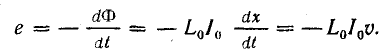
Э. д. с. самоиндукции направлена против тока, т. е. у фронта волны она направлена навстречу напряжению U0 и равна ему по величине 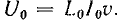
Отношение напряжения к току дает величину волнового сопротивления линии 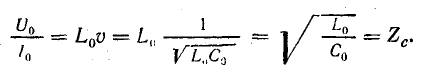
Энергия, отдаваемая источником в линию за единицу времени, 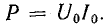
На отрезке линии длиной, равной единице, запасается энергия 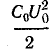
Согласно закону сохранения энергии, мощность источника должна быть равна энергии, запасаемой в электромагнитном поле линии за 1 с: 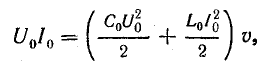
где 
Включение источника постоянного напряжения на линию конечной длины
Пользуясь выводами, полученными ранее, рассмотрим движение волн с учетом возможных отражений от конца линии.
Если линия разомкнута на конце, то коэффициенты отражения ρ и преломления m, согласно формулам (26.28) и (26.30), оказываются равными: ρ = 1; mu = 2; mi = 0. Следовательно, u2 = 2Uпад; i2 = 0.
Отраженная волна напряжения накладывается на падающую, в результате чего напряжение на линии удваивается (рис. 26.8, а).
При этом энергия электромагнитной волны преобразуется в энергию электрического поля.
При коротком замыкании конца линии ρ = —1; mu = 0; mi = 2.
Отраженная волна напряжения компенсирует падающую волну (u2 = 0), а ток в линии удваивается (рис. 26.8, б). Этот процесс сопровождается переходом всей энергии волны в энергию магнитного поля.
При согласованной нагрузке (R2 = Zс) ρ = 0; u2 = Uпад; i2 = Iпад.
Отраженных волн нет, а энергия волны полностью поглощается нагрузкой (рис. 26.8, в).
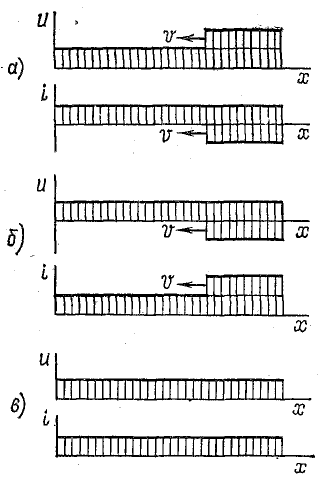
Рис. 26.8. Различные случаи отражения электромагнитной волны с прямоугольным фронтом от конца линии
Электрические цепи с распределенными параметрами
Электрические цепи, параметры которых (сопротивления, индуктивности и емкости) распределены по всей длине, называются цепями с распределенными параметрами.
В неразветвленных цепях с распределенными параметрами токи в разных сечениях неодинаковы. Это происходит вследствие токов утечки между проводами, токов смещения через межпроводные емкости и по ряду других причин. Так как токи утечки пропорциональны напряжению, а токи смещения пропорциональны частоте и напряжению, то с ростом напряжения и частоты их влияние становится более заметным. Кроме того, токи утечки и смещения увеличиваются с увеличением протяженности линии.
К цепям с распределенными параметрами относятся линии электропередачи.
Любая электрическая линия, например двухпроводная линия электропередачи или электросвязи, характеризуется четырьмя первичными параметрами, отнесенными к единице ее длины: активным сопротивлением проводов 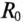
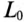
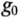
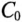
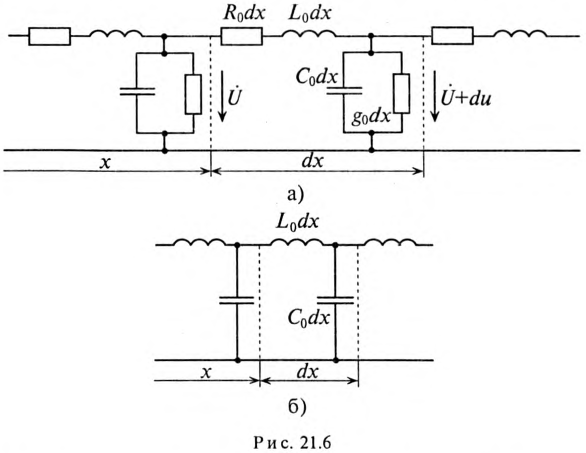
Для исследования длинные линии с распределенными параметрами заменяют схемами замещения (рис. 21.6).
На схеме замещения однородной линии с потерями (рис. 21.6а) рассматривается длинная линия, состоящая из бесконечно большого числа элементарных ячеек длиной dx с параметрами: активным сопротивлением 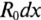
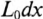
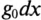
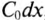
В зависимости от целей и требуемой точности выполненного расчета можно учитывать все четыре параметра или некоторые из них. Например, при исследовании линии электропередачи напряжением 35 кВ и частотой f=50 Гц часто не учитываются токи смещения и утечки, т.е. принимается g0 = 0 и С0 = 0.
При высокой частоте или при коротких импульсах напряжения токи смешения могут быть значительно большими и ими пренебречь нельзя. Но при высокой частоте и малой длине линии можно пренебречь активным сопротивлением R0 и проводимостью g0. При этом получается схема замещения однородной линии без потерь (рис. 21.66).
Исследуя длинную линию электропередачи как цепь с распределенными параметрами, в которой имеются токи утечки и смещения, передачу энергии следует рассматривать как движение электромагнитных волн, или волн тока и напряжения.
При включении генератора в начале линии возникают волны тока и напряжения, которые движутся от генератора (начало линии) к нагрузке (конец линии). Когда электромагнитная волна достигает конца линии, ее энергия лишь частично поглощается нагрузкой. При этом возникают отраженные волны тока и напряжения, перемещающиеся от нагрузки к генератору.
Только при специально подобранном сопротивлении нагрузки вся энергия поглощается нагрузкой и отраженные волны отсутствуют.
Если сопротивление нагрузки в конце линии равно волновому сопротивлению линии, то такая нагрузка называется согласованной. Если же сопротивление нагрузки в конце линии отличается от волнового сопротивления, то нагрузка называется несогласованной. Волновое сопротивление выражается отношением напряжения к току падающих (прямых) или отраженных волн. При согласованной нагрузке отраженных волн в линии нет, т. е. энергия, которую несет падающая электромагнитная волна, полностью поглощается в нагрузке.
При исследовании различных режимов работы длинных линий необходимо учитывать коэффициент отражения р и коэффициент преломления m.
Коэффициент отражения характеризует соотношение между падающими (прямыми) и отраженными волнами напряжения и тока:
Коэффициент преломления в рассматриваемом пункте линии n:
То есть коэффициент преломления m равен отношению комплексов напряжения (тока) в рассматриваемой точке n к комплексу напряжения (тока) падающей волны.
Если на каждую падающую (прямую) волну напряжения и тока накладывается отраженная волна с амплитудой, равной амплитуде падающей волны, то результирующий процесс называют стоячей волной.
Скорость распространения электромагнитных волн в проводах воздушной линии в первом приближении можно считать равной скорости распространения электромагнитных волн в вакууме, т.е. с = 300ООО км/сек.
Расстояние, на которое распространяется электромагнитная волна, или волна тока и напряжения, в течение периода Т, называется длиной волны 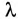
При частоте
При частоте
При частоте
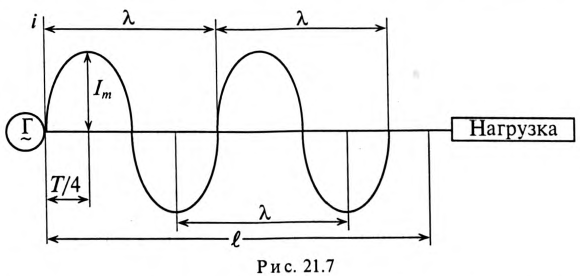
При известной длине волны легко показать распределение тока или напряжения вдоль линии в любой момент времени и без вычислений токов утечки и смещения. Например, при частоте f = 1 МГц и 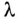
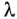
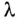
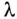
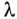
В следующий момент времени характер распределения тока будет таким же, но нулевые и амплитудные значения тока будут наблюдаться в других сечениях линии.
Неодинаковость тока наблюдается только в линиях, длина которых i соизмерима или больше длины волны 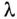
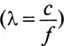
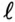
Следовательно, величина тока, проходящего через каждое сечение линии в любой выбранный момент времени, практически одна и та же, т. е. линия слишком «коротка», чтобы в ней можно было заметить неравномерное распределение тока.
При частоте же f = 1 МГц, как показано на рис. 21.7, в той же линии ( 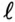
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Резистивные электрические цепи и их расчёт
- Гармонические напряжения и токи
- Энергетические характеристики двухполюсников
- Комплексные функции электрических цепей
- Вращающееся магнитное поле
- Электрические цепи синусоидального тока
- Электрические цепи несинусоидального тока
- Несинусоидальный ток
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Основы радиочастотной электроники. Лекция 1. Теория длинных линийСкачать

Уравнения длинных линий
КОНСПЕКТ ЛЕКЦИЙ
по курсу «Электронные цепи СВЧ»
Содержание
1. Цепи с распределенными параметрами при гармоническом воздействии. 3
1.1. Длинные линии. 3
1.2. Уравнения длинных линий. 4
1.3. Решение уравнений длинных линий. 5
1.4. Входное сопротивление линии. 7
1.5. Волновые процессы в линиях передачи. 9
1.6. Согласование линии передачи. 11
1.7. Условие неискажающей передачи линии. 12
1.8. Волновые матрицы. 13
1.9. Условия нормирования волновых матриц. 15
2. Переходные процессы в цепях с распределенными параметрами. 18
2.1. Уравнение длинной линии во временной области. 18
2.2. Уравнение однородной неискажающей линии в операторной форме. 18
2.3. Решение уравнений однородной неискажающей линии в операторной форме. 19
2.4. Волновые процессы в линии при импульсном воздействии. 20
3. Многополюсники на СВЧ. 21
3.1. Матричное описание распределенных цепей (классическая теория) 21
3.2. Волновые параметры четырехполюсника. 21
3.3. Расчет схемных функций. 22
3.4. Связь между системами параметров. 23
3.5. Условия нормирования волновых матриц. 23
3.6. Шумовые характеристики четырехполюсника. 24
3.7. Волновые шумовые параметры. 25
4. Модели компонентов цепей СВЧ. 27
4.1. Особенности схемных моделей активных компонентов на СВЧ. 27
4.2. Анализ физических процессов в субмикронном ПТШ. 27
4.3. Схемная модель субмикронного полевого транзистора. 28
4.4. Расчет малосигнальных (динамических) крутизны и выходной проводимости. 28
4.5. Расчет малосигнальных входной и проходной емкостей, параметров домена. 29
4.6. Особенности конструкции ПТШ. 30
4.7. Расчет паразитных параметров субмикронного ПТШ. 31
4.8. Линии передачи ИС СВЧ. 32
4.9. Индуктивные элементы ИС СВЧ. 33
4.10. Емкостные элементы ИС СВЧ. 34
4.11. Резистивные элементы ИС СВЧ. 35
4.12. Неоднородности в ИС СВЧ. 35
4.13. Резонаторы. 36
4.14. Фильтры ИС СВЧ. 38
5. Малошумящие цепи СВЧ. 40
5.1. Источники шума в субмикронных ПТШ. 40
5.2. Шумовая схемная модель ПТШ.. 40
5.3. Минимальный коэффициент шума. 41
5.4. Расчет коэффициента усиления по мощности и коэффициента устойчивости 42
5.5. Анализ неоднородностей субмикронных полевых структур. 42
5.6. Уравнения для учета распределенных эффектов в полевых структурах. 43
5.7. Решение уравнений распределенной модели ПТШ.. 43
5.8. Уравнения и матрица проводимости затворной линии. 44
6. Генераторы СВЧ. 45
6.1. Транзисторные генераторы СВЧ колебаний. 45
6.2. Генераторы СВЧ на GaAs ПТШ.. 45
6.3. Автогенераторы СВЧ на туннельных диодах. 47
6.4. Трехточечные схемы автогенераторов на туннельных диодах. 48
Цепи с распределенными параметрами при гармоническом воздействии
Длинные линии
Длинными линиями называют такие линии, геометрическая длина которых больше рабочей длины волны электромагнитных колебаний или соизмерима с ней. Отношение геометрической длины линии к длине рабочей волны называют электрической длины линии. В линиях, в длину которых укладывается одна или несколько длин волн в один и тот же момент ток в проводах линии и напряжение между ними могут иметь не только различную величину, но и напряжение, вследствие этого свойства линии зависят от длины, условий на конце линии (режима холостого хода или короткого замыкания) и характера нагрузки.
Таким образом длинные линии можно рассматривать как цепи с распределенными параметрами. Цепи с распределенными параметрами в отличие от цепей с сосредоточенными параметрами, характеризуются волновыми процессами; при этом величины их описывающие (например, волны тока и напряжения) являются в общем случае функциями времени и пространственных координат.
Различают цепи с объемно-распределенными параметрами, когда все три линейных размера их элементов сравнимы с длиной волны, и линейно-распределенные цепи, в которых только один из линейных размеров сравним с длиной волны, а два остальных существенно меньше ее. Характерными примерами с объемно-распределенных цепей являются волноводы, резонаторы и подобные им элементы техники СВЧ. К классу линейно-распределенных цепей можно отнести двухпроводную и коаксиальную линии, а также такие элементы интегральной техники СВЧ как микрополосковая, копланарная и щелевая линии.
Свойства длинной линии зависят от ее поперечных размеров, пренебрежимо малых в сравнении с длиной волны и свойств среды (диэлектрического заполнения). На рис.1.1 приведены двухпроводная (а) и коаксиальная (б) линии передачи с воздушным заполнением и геометрические размеры, определяющие их свойства.
К линиям, используемым для передачи электромагнитной энергии, предъявляется требование передачи максимальной мощности от источника к нагрузке, при этом вход и выход линии должны быть согласованы. Кроме того, линии должны обеспечивать пропускание достаточно широкого спектра частот для неискажающей передачи импульсных сигналов и иметь при данной передаваемой мощности и частоте минимальные размеры. В общем случае функциональные возможности отрезков линии передачи шире чем передача сигнала от источника к нагрузке. Как будет показано, при некоторых условиях отрезки линии могут рассматриваться как реактивные элементы (индуктивности и емкости), колебательные контуры, частотные фильтры и трансформаторы.
В распределенной линии электрическое и магнитное поля распределены по всей длине линии и потери электромагнитной энергии происходят также по всей длине линии ( в виде тепла, излучения, потерь в диэлектрике).
В дальнейшем будем рассматривать линейные изотропные среды, свойства которых не зависят от интенсивности поля (линейность), и от направления вектора напряженности электрического и магнитного полей (изотропность).
Процесс передачи электромагнитной энергии вдоль проводов линии подобен волновым процессам распространения этой энергии в свободном пространстве, но осуществляется вдоль проводов линии, которые для волн могут рассматриваться как направляющие. Поэтому перенос энергии в линиях передачи можно рассматривать как волновой и описывать как на основе уравнений Максвелла, используя термин напряженностей электрического и магнитного полей, так и на основе уравнений теории цепей, используя понятия волн тока и напряжения.
Во втором случае схемная модель отрезка длинной линии может быть представлена соединением звеньев с сосредоточенными компонентами (рис.1.2), описываемыми погонными параметрами, отнесенными к единице длины: индуктивностью 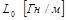
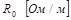
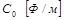
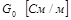
Рис. 1.1 Двухпроводная (а) и коаксиальная (б) линии передачи.
Рис. 1.2 Схемная модель длинной линии.
Если погонные параметры вдоль линии не изменяются, то такую линию называют однородной.
Неоднородность в линии может возникать, например, при изменении ее поперечных размеров или свойств среды, а также при соединении двух линий с различными поперечными размерами.
В случае гармонических колебаний полное погонное сопротивление линии запишется как 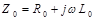
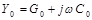
Определим волновое сопротивление через погонные параметры линии рассматривая входное сопротивление дифференциального отрезка линии, нагруженного на сопротивление 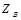
Рис.1.3 К определению волнового сопротивления линии.
Входное сопротивление при последовательно-параллельном соединении элементов запишется:
При 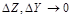
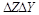
Выражая 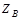
Так как при гармоническом воздействии полное комплексное сопротивление линии может быть записано как 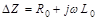
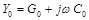
Уравнения длинных линий
При произвольном воздействии токи и напряжения в линии являются как функциями времени 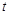
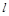
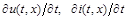
В режиме установившихся гармонических колебаний в линии комплексы тока и напряжения и их производные будут функциями только пространственной координаты ( 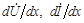
В бесконечно малом отрезке линии длиной 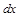
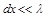
Слагаемое 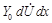
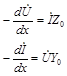
Для решения уравнений (1.1) необходимо разделить переменные. Продифференценцируем телеграфные уравнения по пространственной координате 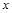
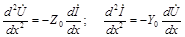
Подставив в эти уравнения значения первых производных из (1.1), получим:
Если обозначить переменной 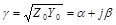
Здесь 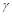
Коэффициент затухания 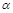
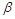
В случае линии без потерь ( 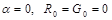
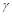
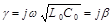
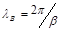
В реальных линиях передачи существует затухание, связанное с потерями в металлических проводниках 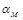
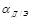
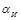
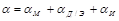
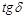

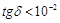
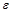
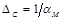
где 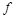
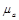
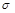
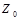
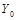
Рис.1.4 Дифференциальный отрезок длинной линии
Видео:Длинные линии │Линии без искажений и потерь │Теория, часть 2Скачать

Длинная линия
Видео:Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Длинная линия
Видео:Последовательное соединение RLC элементов в цепи синусоидального токаСкачать

Содержание
- 1 Дифференциальные уравнения длинной линии
- 1.1 Погонные параметры 1.2 Эквивалентная схема участка длинной линии 1.3 Телеграфные уравнения 1.4 Условие регулярности линии 1.5 Однородные волновые уравнения длинной линии 1.6 Распределение поля падающей волны
2 Комплексный коэффициент отражения по напряжению 3 Коэффициенты бегущей и стоячей волны 4 Входное сопротивление длинной линии 5 Режимы работы длинной линии
- 5.1 Режим бегущей волны 5.2 Режим стоячей волны 5.3 Режим смешанных волн
6 Линия без потерь
- 6.1 Разомкнутая линия 6.2 Замкнутая линия 6.3 Ёмкостная нагрузка 6.4 Индуктивная нагрузка 6.5 Активная нагрузка 6.6 Комплексная нагрузка
7 КПД линии с потерями 8 Пределы применимости теории длинной линии 9 См. также 10 Примечания
Длинная линия — регулярная линия передачи[1], длина которой превышает длину волны (λ) колебаний, распространяющихся в линии.
Характерной особенностью длинных линий является проявление интерференции двух волн, распространяющихся навстречу друг другу. Одна из этих волн создается генератором электромагнитных колебаний, подключенным к линии, и называется падающей. Другая волна может возникать из-за отражения падающей волны от нагрузки, подключенной к противоположному концу линии, и называется отраженной. Отраженная волна распространяется в направлении, обратном падающей волне. Все разнообразие процессов, происходящих в длинной линии, определяется амплитудно-фазовыми соотношениями между падающей и отраженной волнами.
Видео:Лекция 188. Длинная линия: краевые условияСкачать

Дифференциальные уравнения длинной линии
Рассмотрим двухпроводную длинную линию, представленную на рисунке 1. На рисунке обозначено: ZН = RН + iXН — комплексное сопротивление нагрузки; z — продольная координата линии, отсчитываемая от места подключения нагрузки.
Погонные параметры
Рис.1 — К выводу дифференциальных уравнений длинной линии
Из электродинамики известно, что линия передачи может быть охарактеризована ее погонными параметрами:
- R1 — погонное сопротивление, Ом/м; G1 — погонная проводимость, 1/Ом м; L1 — погонная индуктивность Гн/м; C1 — погонная ёмкость Ф/м;
Погонные сопротивление R1 и проводимость G1 зависят от проводимости материала проводов и качества диэлектрика, окружающего эти провода, соответственно. Чем меньше тепловые потери в металле проводов[2] и в диэлектрике, тем меньше соответственно, R1[3] и G1[4]. Погонные индуктивность L1 и емкость C1 определяются формой и размерами поперечного сечения проводов, а также расстоянием между ними.
Эквивалентная схема участка длинной линии
Рис.2 — Эквивалентная схема участка длинной линии
Выделим из линии элементарный участок бесконечно малой длины dz и рассмотрим его эквивалентную схему, покзанную на рисунке 2. На этой схеме стрелками обозначены направления отсчета напряжения U и тока I в линии; dU и dI — приращения напряжения и тока в линии на элементе длины dz. Значения параметров схемы определяются соотношениями:
Используя эквивалентную схему, запишем выражения для приращений напряжения и тока:
Подставляя сюда значения параметров схемы из (1), получаем:

где Z1 = R1 + iωL1, Y1 = G1 + iωC1 — погонные комплексные сопротивление и проводимость линии. Из последних соотношений находим дифференциальные уравнения линии:
Телеграфные уравнения
Основная статья: Телеграфное уравнение
Эти соотношения называются телеграфными уравнениями длинной линии. Они определяют связь между током и напряжением в любом сечении линии. Решим телеграфные уравнения относительно напряжения и тока. Для этого продифференцируем их по z:
При этом учтем, что:
Условие регулярности линии
Данные соотношения являются математическим определением регулярности длинной линии. Смысл соотношения (4) состоит в неизменности вдоль линии ее погонных параметров.
Подставляя в (3) значения производных напряжения и тока из (2), после преобразований получаем:
Однородные волновые уравнения длинной линии

где γ — коэффициент распространения волны в линии: 
Соотношения (5) называются однородными волновыми уравнениями длинной линии. Их решения известны и могут быть записаны в виде:

где AU, BU и AI, BI — коэффициенты, имеющие единицы измерения напряжения и тока соответственно, смысл которых будет ясен ниже.
Решения волновых уравнений в виде (3.6) имеют весьма характерный вид: первое слагаемое в этих решениях представляет собой падающую волну напряжения или тока, распространяющуюся от генератора к нагрузке, второе слагаемое — отраженную волну, распространяющуюся от нагрузки к генератору. Таким образом, коэффициенты AU, AI представляют собой комплексные амплитуды падающих волн напряжения и тока соответственно, а коэффициенты BU, BI — комплексные амплитуды отраженных волн напряжения и тока соответственно. Так как часть мощности, передаваемой по линии, может поглощаться в нагрузке, то амплитуды отраженных волн не должны превышать амплитуды падающих:
Направление распространения волн в (6) определяется знаком в показателях степени экспонент: плюс — волна распространяется в отрицательном направлении оси z; минус — в положительном направлении оси z (см. рис. 1).Так, например, для падающих волн напряжения и тока можно записать:

Коэффициент распространения волны в линии γ в общем случае является комплексной величиной и может быть представлен в виде:

где α — коэффициент затухания волны[5] в линии; β — коэффициент фазы[6]. Тогда соотношение (7) можно переписать в виде:

Так как при распространении падающей волны на длину волны в линии λЛ фаза волны изменяется на 2π , то коэффициент фазы можно связать с длиной волны λЛ соотношением

При этом фазовая скорость волны в линии VФ определяется через коэффициент фазы:

Определим коэффициенты A и B , входящие в решения (6) волновых уравнений, через значения напряжения UН и тока IН на нагрузке. Это является оправданным, так как напряжение и ток на нагрузке практически всегда можно измерить с помощью измерительных приборов. Воспользуемся первым из телеграфных уравнений (2) и подставим в него напряжение и ток из (6). Тогда получим:
Сравнив коэффициенты при экспонентах с одинаковыми показателями степеней, получим:

где 
Перепишем (6) с учетом (12):

Для определения коэффициентов A и B в этих уравнениях воспользуемся условиями в конце линии z = 0:

Тогда из (13) при z = 0 найдем

Подставив полученные значения коэффициентов из (14) в (13), после преобразований получим:

При выводе (15) учтены определения гиперболических синуса и косинуса[8].
Соотношения для напряжения и тока (15) так же, как и (6), являются решениями однородных волновых уравнений. Их отличие состоит в том, что напряжение и ток в линии в соотношении (6) определены через амплитуды падающей и отраженной волн, а в (15) — через напряжение и ток на нагрузке.
Рассмотрим простейший случай, когда напряжение и ток в линии определяются только падающей волной, а отраженная волна отсутствует[9]. Тогда в (6) следует положить BU = 0, BI = 0:

Распределение поля падающей волны
Рис.3. Эпюры напряжений падающей волны в длинной линии. а) амплитуда; б) фаза
На рис.3. представлены эпюры изменения амплитуды |U| и фазы φU апряжения вдоль линии. Эпюры изменения амплитуды и фазы тока имеют такой же вид. Из рассмотрения эпюр следует, что при отсутствии в линии потерь (α[5] = 0) амплитуда напряжения в любом сечении линии остается одной и той же. При наличии потерь в линии (α[5] > 0) часть переносимой мощности преобразуется в тепло (нагревание проводов линии и окружающего их диэлектрика). По этой причине амплитуда напряжения падающей волны экспоненциально убывает в направлении распространения.
Фаза напряжения падающей волны φU = β z изменяется по линейному закону и уменьшается по мере удаления от генератора.
Рассмотрим изменение амплитуды и фазы, например, напряжения при наличии падающей и отраженной волн. Для упрощения положим, что потери в линии отсутствуют, то есть α[5] = 0. Тогда напряжение в линии можно представить в виде:

где Γ = BU / AU — комплексный коэффициент отражения по напряжению.
Видео:Длинные линии │Цепи с распределенными параметрами │Теория, часть 1Скачать

Комплексный коэффициент отражения по напряжению
Характеризует степень согласования линии передачи с нагрузкой. Модуль коэффициента отражения изменяется в пределах:
- | Г | = 0, если отражения от нагрузки отсутствуют и BU = 0[9]; | Г | = 1, если волна полностью отражается от нагрузки, то есть | AU | = | BU | ;
Соотношение (16) представляет собой сумму падающей и отраженной волн.
Рис.4. Векторная диаграмма напряжений в линии с отраженной волной
Отобразим напряжение на комплексной плоскости в виде векторной диаграммы, каждый из векторов которой определяет падающую, отраженную волны и результирующее напряжение (рис. 4). Из диаграммы видно, что существуют такие поперечные сечения линии, в которых падающая и отраженная волны складываются в фазе. Напряжение в этих сечениях достигает максимума, величина которого равна сумме амплитуд падающей и отраженной волн:

Кроме того, существуют такие поперечные сечения линии, в которых падающая и отраженная волны складываются в противофазе. При этом напряжение достигает минимума:

Если линия нагружена на сопротивление, для которого |Г| = 1 , т. е. амплитуда падающей и отраженной волн равны |BU| = |AU|, то в этом случае Umax = 2|AU|, а Umin = 0.
Рис.5. Эпюры распределения напряжения вдоль линии с отражённой волной. а) Модуль напряжения; б) фаза напряжения.
Напряжение в такой линии изменяется от нуля до удвоенной амплитуды падающей волны. На рис. 5 представлены эпюры изменения амплитуды и фазы напряжения вдоль линии при наличии отраженной волны.
Видео:Длинные Линии. Удвоитель напряжения. Режимы работы линии, КЗ, ХХ. Практика.Скачать

Коэффициенты бегущей и стоячей волны
По эпюре напряжения судят о степени согласования линии с нагрузкой. Для этого вводятся понятия коэффициента бегущей волны — kБВ и коэффициента стоячей волны kСВ:
Эти коэффициенты, судя по определению, изменяются в пределах:


На практике наиболее часто используется понятие коэффициента стоячей волны, так как современные измерительные приборы (панорамные измерители kСВ) на индикаторных устройствах отображают изменение именно этой величины в определенной полосе частот.
Видео:Активное и реактивное сопротивление в цепи переменного тока. 11 класс.Скачать

Входное сопротивление длинной линии
Входное сопротивление линии — является важной характеристикой, которое определяется в каждом сечении линии как отношение напряжения к току в этом сечении:
Так как напряжение и ток в линии изменяются от сечения к сечению, то и входное сопротивление линии изменяется относительно ее продольной координаты z. При этом говорят о трансформирующих свойствах линии, а саму линию рассматривают как трансформатор сопротивлений. Подробнее свойство линии трансформировать сопротивления будет рассмотрено ниже.
Видео:Линии с распределёнными параметрами в статических режимах работыСкачать

Режимы работы длинной линии
Различают три режима работы линии:
режим бегущей волны; [10] режим стоячей волны; [10] режим смешанных волн.
Режим бегущей волны
Режим бегущей волны характеризуется наличием только падающей волны, распространяющейся от генератора к нагрузке. Отраженная волна отсутствует. Мощность, переносимая падающей волной, полностью выделяется в нагрузке. В этом режиме BU = 0, | Г | = 0, kбв =kсв = 1[10].
Режим стоячей волны
Режим стоячей волны характеризуется тем, что амплитуда отраженной волны равна амплитуде падающей BU = AU т. е. энергия падающей волны полностью отражается от нагрузки и возвращается обратно в генератор. В этом режиме, | Г | = 1, kсв = 
Режим смешанных волн
В режиме смешанных волн амплитуда отраженной волны удовлетворяет условию 0 W Сопротивление нагрузки меньше волнового сопротивления линии RН
🎦 Видео
Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Лекция 185. Уравнения для длинных линийСкачать

Лекция 101-1. Линии с распределенными параметрами. Первичные параметры и основные уравненияСкачать

Пример 7 | Классический метод расчета цепи 1-го порядка с конденсаторомСкачать

Расчет цепи переменного тока БЕЗ комплексных чиселСкачать

Урок 358. Активное сопротивление в цепи переменного тока. Действующее значение тока и напряженияСкачать

Длинная линия. Что там внутри?Скачать

Длинная линияСкачать

Билет №37 "Двухпроводная линия"Скачать

Расчет переходного процесса через ДИФФЕРЕНЦИАЛЬНОЕ уравнение по законам Кирхгофа│Классический методСкачать