Концентрацию растворов сильных электролитов можно характеризовать
не только активностью а, но и ионной силой. Активность а показывает
концентрацию одного электролита в растворе, а через ионную силу можно
выражать концентрацию как одного, так и нескольких электролитов. Таким
образом, ионная сила показывает суммарную концентрацию всех
электролитов в растворе с учетом взаимодействия между ионами.
Ионная сила раствора (I, размерность концентрации) – это полусумма
произведений концентраций всех ионов в растворе на квадрат их заряда.
— моляльность i-го иона;
m – моляльность электролита; Z
заряд i-го иона.
Пример: раствор содержит 0,001 моль
Видео:Степень электролитической диссоциации. Сильные и слабые электролиты. 9 класс.Скачать
Понятие о теории сильных электролитов
Электролиты — это вещества, способные распадаться на ионы в расплаве или растворе. Распад на ионы называется диссоциацией. Диссоциация слабых электролитов подчиняется закону действующих масс и количественно характеризуется константой диссоциации. Особенности процессадиссоциации разбавленных растворов слабых электролитов достаточно хорошо описываются классической теорией электролитической диссоциации Аррениуса. Эта теория не сразу получила признание, т.к. не объясняла причин диссоциации. А ведь энергетические затраты на ионизацию твердых солей довольно велики
100 ¸ 200 кДж/моль. Впоследствии было установлено, что энергетические затраты на разрушение кристаллической решетки при растворении кристаллов, на диссоциацию кислот и солей компенсируются энергией сольватации ионов.
К началу ХХ века теория электролитической диссоциации достигла больших успехов. Однако поведение концентрированных растворов слабых электролитов и растворов сильных электролитов количественно описать с позиций теории Аррениуса невозможно.
Многие аномалии в свойствах растворов сильных электролитов связаны с полной диссоциацией молекул сильных электролитов. Это приводит к возникновению межионного взаимодействия, т.к. концентрация ионов в растворе намного выше, чем у слабых электролитов.
Необходимо отметить, что непостоянство Кд наблюдается и у слабых электролитов уже при умеренных концентрациях. И оно тоже связано с межионным взаимодействием, не предусмотренным теорией Аррениуса.
Теория электролитической диссоциации не могла объяснить и солевой эффект. Этот и другие явления можно объяснить с помощью теории Дебая – Хюккеля (1923 г).
В теории электролитов важным является вопрос о распределении ионов в растворе. Теория электролитической диссоциации Аррениуса рассматривает ионы в растворе, находящиеся в состоянии беспорядочного движения. Это не соответствует действительности, т.к. не учитывается электростатическое взаимодействие между ионами.
Электрические силы проявляются на больших расстояниях, а в растворах сильных электролитов концентрация ионов большая, расстояния между ионами невелики. Поэтомумежионное взаимодействие влияет на распределение ионов.
В распределении ионов будут участвовать два вида движения: беспорядочное тепловое и упорядоченное электростатическое, энергии которых сравнимы по величине.
Конкуренция этих двух видов движения приводит к тому, что реальное распределение является промежуточным между хаотическим и упорядоченным, что создает трудности при создании теории электролитов. Электростатическое притяжение разноименно заряженных и отталкивание одноименно заряженных ионов приводит к тому, что вокруг положитель-но заряженного иона с большей вероятностью располагаются отрицатель-но заряженные ионы, а вокруг отрицательно заряженного иона распола-гается больше положительно заряженных ионов. При этом раствор в целом остается электронейтральным.
Эти представления Дебай и Хюккель сформулировали в виде идеи о наличии ионной атмосферы вокруг каждого иона, состоящей из положи-тельно и отрицательно заряженных ионов. Электростатическая теория раз-бавленных растворов сильных электролитов Дебая — Хюккеля учитывает также взаимодействие ионов друг с другом.
Основные положения теории Дебая-Хюккеля:
1) электролит диссоциирован полностью (a = 1);
2) растворитель представляет собой непрерывную среду, т.е. не учитывает-ся изменение диэлектрической проницаемости среды в результате образования раствора;
3) ионы взаимодействуют по закону Кулона, т.е. ионы рассматриваются как материальные точки (собственным объемом ионов пренебрегают);
4) электростатическое взаимодействие рассматривается как взаимодейст-вие между центральным ионом и его ионной атмосферой;
5) из всех свойств ионов учитывается только заряд.
Рассмотрим положение катиона в растворе и образование ионной атмосферы:
Вокруг каждого катиона располагаются другие ионы и (–) и (+), но вероятность нахождения анионов возле центрального катиона больше. В целом система будет электронейтральна. В теории Дебая-Хюккеля остает-ся неучтенным целый ряд взаимодействий и свойств ионов: сольватация ионов, особенности строения ионов (многие ионы состоят из нескольких структурных единиц и имеют неравномерное распределение заряда), их поляризуемость. Это ограничивает применимость теории.
Тем не менее, ионная атмосфера – реально существующая система в растворах электролитов. Она обладает следующими характерными особенностями:
1) в состав ионной атмосферы входят катионы и анионы, причем суммарный заряд ионной атмосферы равен по величине заряду централь-ного иона и противоположен ему по знаку;
2) все ионы в растворе равноправны, поэтому каждый является центральным и одновременно входит в состав ионной атмосферы другого иона:
3) ионная атмосфера носит статистический характер, т. е. в следствие теплового движения ионов происходит постоянный обмен местами ионов из атмосферы с ионами, находящимися за ее пределами.
Распределение избыточного заряда в ионной атмосфере дискретно, но теория Дебая — Хюккеля рассматривает ионную атмосферу, как непре-рывную, заряд которой «размазан» по всему пространству, убывая по мере удаления от центрального иона.
Теория Дебая – Хюккеля позволяет рассчитать некоторую величину X (хи), связанную с термодинамическими свойствами ионов
X = 
,
где хi – число ионов в единице объема, 1 см 3 ;
,
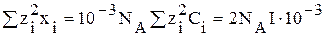
где Сi – концентрация ионов, моль/л.
Величина 
называется толщинойионной атмосферы.
Толщина ионной атмосферы зависит от температуры, диэлектрической проницаемости (e) растворителя, числа и заряда ионов.
Причем, X связано с электрохимическим потенциалом 
.
Если ион находится в покое, ионная атмосфера пребывает в стационарном состоянии и имеет сферическую поверхность. При движении иона впереди него непрерывно образуется новая атмосфера, а позади — разрушается старая. Этот процесс быстрый, но не мгновенный. Он характеризуется некоторым временем релаксации, т.е. ионная атмосфера теряет шаровую симметрию и возникает электростатическая сила, препятствующая движению центрального иона. Таким образом возникает релаксационный эффект торможения. Время релаксации – это время, за которое избыточная концентрация ионов в ионной атмосфере при распаде или возникновении ее изменится в е раз, е = 2,73.
На ион, двигающийся в электрическом поле, действуют две силы:
1) Сила электрического поля,
где V – градиент потенциала поля , z – заряд иона.
2) Сила вязкого сопротивления среды (растворителя),
где k — коэффициент трения,
u – скорость движения иона.
Эти две силы уравновешивают друг друга Fo = F и ион движется равномерно.
Кроме того, на движущийся ион действуют тормозящие силы, обусловленные электростатическим взаимодействием ионов и их ионных атмосфер (электрофоретическое торможение).
Электрофоретическая сила торможения Fэ возникает потому, что ионная атмосфера, имея противоположный центральному иону заряд, движется ему навстречу под действием внешнего поля. К тому же, ионы — гидратированы, т.е. ионная атмосфера будет увлекать за собой центральный ион.
Движение катионов тормозится, и это торможение называется электро-форетическим. Во время движения центрального иона из-за несим-метричности ионной атмосферы возникает уменьшение градиента потенциала внешнего поля на величину DV, т.е. возникает тормозящая сила Fр. Этот вид торможения называется релаксационным.Таким образом, при равновесии сил, действующих на ион
Силы релаксационного и электрофоретического торможения опреде-ляются ионной силой раствора, природой растворителя и температурой. Для одного и того же электролита при прочих постоянных условиях эти силы возрастают с ростом концентрации..
Электростатическая теория сильных электролитов позволяет вычис-лить коэффициент активности отдельного иона gi и g± (средний коэффициент активности).
Например, для бинарного раствора
, (7.44)
где А = 1,825 × 10 6 (e × p) –3/2 ;
e — диэлектрическая проницаемость растворителя.
В разбавленном водном растворе при 298 К e = 78,3 и
Это уравнение (7.44) применимо только к сильно разбавленным растворам электролитов и называется предельным законом Дебая-Хюккеля. Оно теоретически обосновывает правило ионной силы.
Т.е. при данной ионной силе раствора среднеионный коэффициент активности электролита в сильно разбавленном растворе является постоянной величиной.
Предельный закон Дебая – Хюккеля, в связи с приближениями физической модели и математическими допущениями при выводе, справедлив лишь в растворах с ионной силой I 2 /eq = 2kT ® r = z1z2e 2 /2ekT,
где r — максимальное расстояние между ионами.
Для водных растворов электролитов типа 1,1 при 25°С r = 3,57 
. Т.е. ионные пары образуются, если расстояние между ионами меньше 3,57 .
Видео:Ионная сила раствора. Теория (кратко) + задача.Скачать
Уравнения дебая хюккеля и дэвиса
Дебай и Хюккель, предложив модель, которая легла в основу теории сильных электролитов, постулировали:
Электролит полностью диссоциирует, но в сравнительно разбавленных растворах ().
Каждый ион окружен оболочкой из ионов противоположного знака. В свою очередь, каждый из этих ионов сольватирован. Это окружение называется ионной атмосферой.
Очевидно, что при электростатическом взаимодействии ионов противоположных знаков необходимо учитывать влияние ионной атмосферы. При движении катиона в электростатическом поле ионная атмосфера деформируется; она сгущается перед ним и разрежается позади него. Эта асимметрия ионной атмосферы оказывает тем более тормозящее действие движению катиона, чем выше концентрация электролитов и чем больше заряд ионов. В этих системах само понятие концентрации становится неоднозначиным и должно заменяться активностью. Для бинарного одно-однозарядного электролита активности катиона () и аниона () соответственно равны
 |
где и – аналитические концентрации соответственно катиона и аниона, γ+ и γ– – их коэффициенты активности.
Определить активности каждого иона в отдельности невозможно, поэтому для одно-однозарядных электролитов пользуются средними геометрическими значений активностей и коэффициентов активностей:
  |
Коэффициент активности по Дебаю–Хюккелю зависит по крайней мере от температуры, диэлектрической проницаемости растворителя (ε) и ионной силы (); последняя служит мерой интенсивности электрического поля, создаваемого ионами в растворе.
Для данного электролита ионная сила выражается уравнением Дебая–Хюккеля:
|
Ионная сила в свою очередь равна
|
Здесь – аналитическая концентрация, – заряд катиона или аниона. Для одно-однозарядного электролита ионная сила совпадает с концентрацией. Таким образом, NaCl и Na2SO4 при одинаковых концентрациях будут иметь разные ионные силы. Сопоставление свойств растворов сильных электролитов можно проводить только тогда, когда ионные силы одинаковы; даже небольшие примеси резко изменяют свойства электролита.
На рис. 6.6 сопоставляются вычисленные и экспериментальные значения lg γ± при различных ионных силах. Из него видно, что уравнение Дебая–Хюккеля выполняется только для разбавленных растворов.
 1 |
| Рисунок 6.6 Пунктирные прямые рассчитаны по уравнению Дебая–Хюккеля. Знание коэффициентов активностей позволяет оценить реальные свойства сильных электролитов. 🌟 Видео4 1 Представления Дебая Хюккеля 4 1 Представления Дебая Хюккеля Содержание курса Analytical chemСкачать  Решить задачу Коши для дифференциального уравнения с помощью формулы ДюамеляСкачать  сильные и слабые электролиты РАСЧЕТ рНСкачать  Основные положения теории электролитической диссоциации. Свойства ионов. 9 класс.Скачать  Метод половинного деления решение нелинейного уравненияСкачать  Задача. Ионная сила, активность ионовСкачать  Теории кислот, оснований и растворов. Теория Аррениуса-Оствальда. 11 класс.Скачать  Применение теории растворов электролитов и закона действующих масс в аналитической химии.Скачать  3.1 Формула Даламбера, решение волнового уравнения на бесконечной прямойСкачать  Теория теплоемкости ДебаяСкачать  Линейные диофантовы уравненияСкачать  Органическая химия. Подробный разбор задач ВУЗа. ММОХ (метод молекулярных орбиталей Хюккеля).Скачать  Буферные растворы. 1 часть. 11 класс.Скачать  ПЕРЕЧНЕВЫЕ ОЛИМПИАДЫ. Диофантовы уравненияСкачать  Остаток от деления 14^245 на 90 | Теорема Эйлера | Теория чисел | КАК РЕШАТЬ?Скачать  Алгоритм ЕвклидаСкачать  Метод половинного деления. ДихотомияСкачать  |